25.6相似三角形的应用同步达标测评 2021-2022学年冀教版九年级数学上册(Word版 含答案)
文档属性
| 名称 | 25.6相似三角形的应用同步达标测评 2021-2022学年冀教版九年级数学上册(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 357.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-14 11:25:30 | ||
图片预览




文档简介
2021-2022学年冀教版九年级数学上册《25.6相似三角形的应用》同步达标测评(附答案)
一.选择题(共10小题,满分40分)
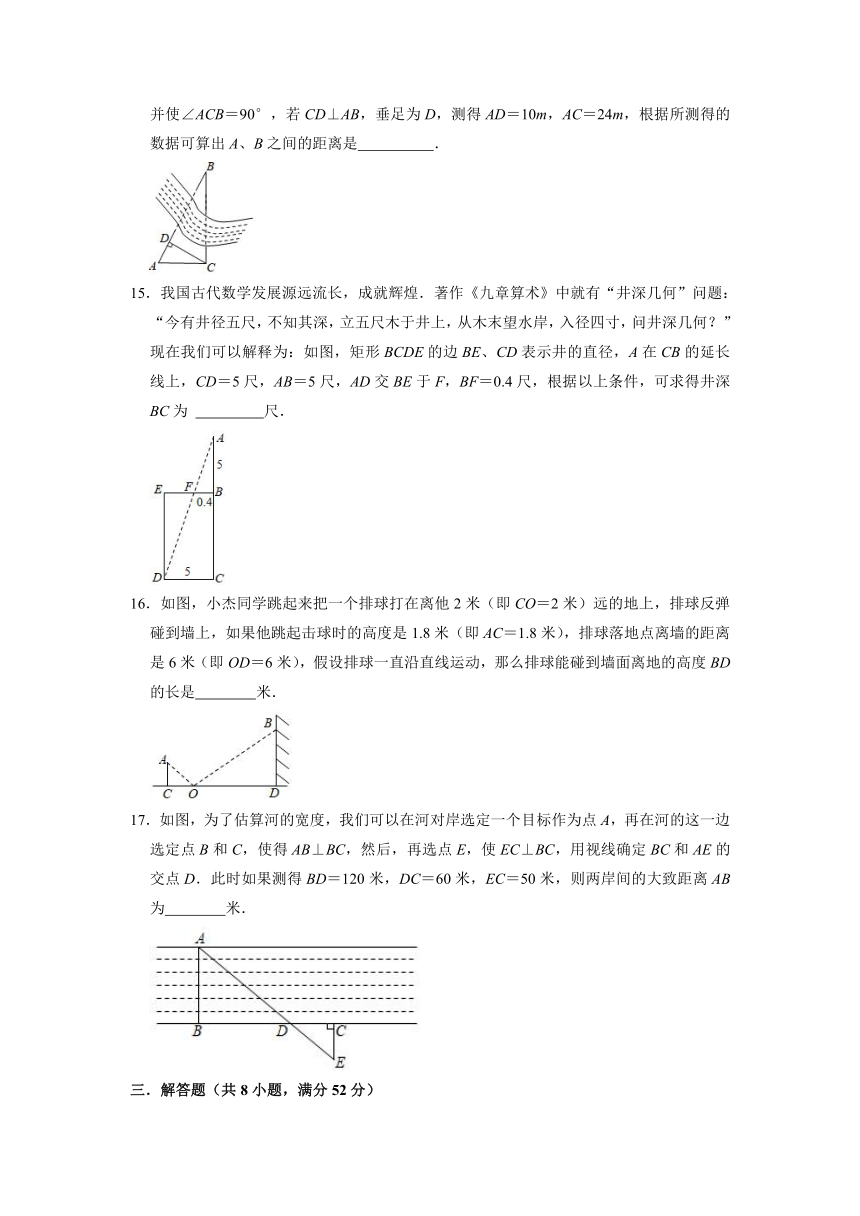
1.如图是装了液体的高脚杯示意图(数据如图)用去一部分液体后如右图所示,此时液面直径AB=( )
A.2cm B.2.5cm C.3cm D.4cm
2.一个直角三角形木架的两条直角边的边长分别是30cm,40cm.现要做一个与其相似的三角形木架,如果以60cm长的木条为其中一边,那么另两边中长度最大的一边最多可达到( )
A.60cm B.75cm C.100cm D.120cm
3.大约在两千四五百年前,如图1墨子和他的学生做了世界上第1个小孔成倒像的实验.并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.如图2所示的小孔成像实验中,若物距为10cm,像距为15cm,蜡烛火焰倒立的像的高度是6cm,则蜡烛火焰的高度是( )
A.3cm B.4cm C.6cm D.9cm
4.如图,在测量旗杆高度的数学活动中,某同学在脚下放了一面镜子,然后向后退,直到他刚好在镜子中看到旗杆的顶部.若眼睛距离地面AB=1.5m,同时量得BC=2m,CD=12m,则旗杆高度DE=( )
A.6m B.8m C.9m D.16m
5.如图,数学兴趣小组利用硬纸板自制的Rt△ABC来测量操场旗杆MN的高度,他们通过调整测量位置,并使边AC与旗杆顶点M在同一直线上,已知AC=0.8米,BC=0.5米,目测点A到地面的距离AD=1.5米,到旗杆的水平距离AE=20米,则旗杆MN的高度为( )
A.12米 B.12.5米 C.14米 D.15米
6.如图,为估算某河的宽度,在河对岸选定一个目标点A,在近岸取B,C,D三点,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上,若测得BE=20m,CE=10m,CD=20m,则河的宽度为( )
A.20m B.30m C.40m D.60m
7.《九章算术》是中国古代的数学专著,它奠定了中国古代数学的基本框架,以计算为中心,密切联系实际,以解决人们生产、生活中的数学问题为目的.书中记载了这样一个问题:“今有勾五步,股十二步,问勾中容方几何.”其大意是:如图,Rt△ABC的两条直角边的长分别为5和12,则它的内接正方形CDEF的边长为( )
A. B. C. D.
8.如图,一束平行的阳光从教室窗户射入,小兵同学量出BC=1m,NC=m,BN=m,AC=4.5m,MC=6m,则MA的长为( )
A.5m B.7.5m C.6m D.5.5m
9.如图是一块三角形钢材ABC,其中边BC=60cm,高AD=40cm,把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,则这个正方形零件的边长是( )
A.16 B.24 C.30 D.36
10.《九章算术》中,有一数学史上有名的测量问题:“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”今译如下:如图,矩形ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E,南门点F分别位于AB,AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH的长为( )
A.0.95里 B.1.05里 C.2.05里 D.2.15里
二.填空题(共7小题,满分28分)
11.小明身高是1.6m,影长为2m,同时刻教学楼的影长为24m,则楼的高是 .
12.在上午的某一时刻身高1.7米的小刚在地面上的投影长为3.4米,小明测得校园中旗杆在地面上的影子长16米,还有2米影子落在墙上,根据这些条件可以知道旗杆的高度为 米.
13.如图所示,D、E之间要挖建一条直线隧道,为计算隧道长度,工程人员在线段AD和AE上选择了测量点B,C,已知测得AD=100,AE=200,AB=40,AC=20,BC=30,则通过计算可得DE长为 .
14.如图,为测量小河两岸A、B两点之间的距离,在小河一侧选出一点C观测A、B两点,并使∠ACB=90°,若CD⊥AB,垂足为D,测得AD=10m,AC=24m,根据所测得的数据可算出A、B之间的距离是 .
15.我国古代数学发展源远流长,成就辉煌.著作《九章算术》中就有“井深几何”问题:“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”现在我们可以解释为:如图,矩形BCDE的边BE、CD表示井的直径,A在CB的延长线上,CD=5尺,AB=5尺,AD交BE于F,BF=0.4尺,根据以上条件,可求得井深BC为 尺.
16.如图,小杰同学跳起来把一个排球打在离他2米(即CO=2米)远的地上,排球反弹碰到墙上,如果他跳起击球时的高度是1.8米(即AC=1.8米),排球落地点离墙的距离是6米(即OD=6米),假设排球一直沿直线运动,那么排球能碰到墙面离地的高度BD的长是 米.
17.如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选定点B和C,使得AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,EC=50米,则两岸间的大致距离AB为 米.
三.解答题(共8小题,满分52分)
18.如图,阳光通过窗口照到室内,在地面上留下的亮区宽DE=2.7m,已知亮区一边到窗下的墙脚距离CE=8.7m,窗高AB=1.8m,那么窗口底边离地面的高度BC是多少?
19.如图,阳光通过窗口照到室内,在地面上留下一段亮区.已知亮区一边到窗下的墙脚距离CE=3.6m,窗高AB=1.2m,窗口底边离地面的高度BC=1.5m,求亮区ED的长.
20.如图,AB和CD表示两根直立于地面的柱子,AD和BC表示起固定作用的两根钢筋,AD与BC的交点为M,已知AB=10m,CD=15m,求点M离地面的高度MH.
21.如图,小明测得树AB落在水平地面上的影长BC为 2.4 米,落在坡面上的影长CE为3.2米,身高是1.6米的小明站在坡面上,影子也都落在坡面上,长度为2米.已知坡面的铅直高度CH与水平距离DH的比为3:4,试求树AB的高度.
22.同一时刻甲、乙两组同学在阳光下进行测量,甲组将一根长为2.4m的竹竿EF直立于平地,测得竹竿的影长FG为1.8m;摩天轮的立柱OB直立于平地,乙组测得立柱OB的影长BC为36m,摩天轮在立柱右侧影子的边缘D与立柱OB相距86m,求摩天轮的半径和最高点A的高.
23.如图,△ABC是一块锐角三角形材料,BC=200mm,高AD=150mm,要把它加工成一矩形零件,使矩形一边在BC上,其余两个顶点分别在AB、AC上.
(1)设PN=x,矩形PQMN的面积为S,求S关于x的函数表达式,并指出x的取值范围.
(2)当x为何值时,矩形PQMN的面积最大?最大值是多少?
24.如图,某校宣传栏BC后面12米处种有一排与宣传栏平行的若干棵树,即BC∥ED,且相邻两棵树的间隔为2米,一人站在距宣传栏前面的A处正好看到两端的树干,其余的树均被宣传栏挡住.已知AF⊥BC,AF=3米,BC=10米,求该宣传栏后DE处共有多少棵树?(不计宣传栏的厚度).
25.小明用如图所示的方式测量一幢楼高:线段AB、EF、CD分别表示人、竹、竿、楼房的高度,且A、C、E在一条直线上.测得人和竹竿的水平距离为1.5m,人和楼房的水平距离为20m,人的高度为1.6m,竹竿的高度为2.8m,求这幢楼的高度.
参考答案
一.选择题(共10小题,满分40分)
1.解:如图:过O作OM⊥CD,垂足为M,过O′作O′N⊥AB,垂足为N,
∵CD∥AB,
∴△CDO∽ABO′,即相似比为,
∴=,
∵OM=15﹣7=8(cm),O′N=11﹣7=4(cm),
∴=
∴AB=3(cm),
故选:C.
2.解:∵一个直角三角形木架的两条直角边的边长分别是30cm,40cm,
∴三角形的斜边长为:=50(cm),
∵现要做一个与其相似的三角形木架,以60cm长的木条为其中一边,
∴当另两边中长度最大的一边最长,则两三角形的相似比为:30:60=1:2,
故设要做的三角形最长边长为:50×2=100(cm).
故选:C.
3.解:设蜡烛火焰的高度是xcm,
由相似三角形的性质得到:=.
解得x=4.
即蜡烛火焰的高度是4cm.
故选:B.
4.解:∵AB⊥BD,DE⊥BD,
∴∠ABC=∠EDC=90°,
∵∠ACB=∠DCE,
∴△ABC∽△EDC,
∴=,
∴=,
∴DE=9(m),
故选:C.
5.解:∵∠CAB=∠EAM,∠ACB=∠AEM=90°,
∴△ACB∽△AEM,
∴=,
∴=,
∴EM=12.5(米),
∵四边形ADNE是矩形,
∴AD=EN=1.5(米),
∴MN=ME+EN=12.5+1.5=14(米).
故选:C.
6.解:∵AB⊥BC,CD⊥BC,
∴△BAE∽△CDE,
∴,
∵BE=20m,CE=10m,CD=20m,
∴,
解得:AB=40,
故选:C.
7.解:∵四边形CDEF是正方形,
∴CD=ED,DE∥CF,
设ED=x,则CD=x,AD=5﹣x,
∵DE∥CF,
∴∠ADE=∠C,∠AED=∠B,
∴△ADE∽△ACB,
∴=,
∴=,
∴x=,
∴正方形CDEF的边长为.
故选:B.
8.解:∵BN∥AM,
∴△BCN∽△ACM,
∴=,
∵BC=1m,BN=m,AC=4.5m,
∴=,
∴MA=7.5(m).
故选:B.
9.解:∵四边形EGHF为正方形,
∴BC∥EF,
∴△AEF∽△ABC;
设正方形零件的边长为x cm,则KD=EF=xcm,AK=(40﹣x)cm,
∵AD⊥BC,
∴=,
∴=,
解得:x=24.
即:正方形零件的边长为24cm.
故选:B.
10.解:EG⊥AB,FH⊥AD,HG经过A点,
∴FA∥EG,EA∥FH,
∴∠HFA=∠AEG=90°,∠FHA=∠EAG,
∴△GEA∽△AFH,
∴=,
∵AB=9里,DA=7里,EG=15里,
∴FA=3.5里,EA=4.5里,
∴=,
解得:FH=1.05里.
故选:B.
二.填空题(共7小题,满分28分)
11.解:设教学楼高度为xm,
列方程得:
解得x=19.2,
故教学楼的高度为19.2m.
故答案为:19.2m.
12.解:∵==,
∵CE=2,
∴CD=4,
∴BD=BC+CD=16+4=20米.
∴AB=BD=×20=10米.
故应填10.
13.解:∵AD=100,AE=200,AB=40,AC=20,
∴==,==,
∴=,
而∠BAC=∠EAD,
∴△ABC∽△EAD,
∴=,
∴DE=5BC=5×30=150.
故答案为150.
14.解:∵∠ACB=90°、CD⊥AB,
∴∠ACB=∠ADC=90°,
∴∠A+∠B=∠A+∠ACD=90°,
则∠B=∠ACD,
∴△ACD∽△ABC,
∴=,即=,
解得:AB=57.6(m),
故答案为:57.6.
15.解:设BC=x尺.
∵四边形BCDE是矩形,
∴BF∥CD,
∴△AFB∽△ADC,
∴=,
∴=,
解得x=57.5,
经检验:x=57.5是分式方程的解.
∴BC=57.5(尺).
故答案为:57.5.
16.解:由题意得:∠AOC=∠BOD.
∵AC⊥CD,BD⊥CD,
∴∠ACO=∠BDO=90°.
∴△ACO∽△BDO.
∴.
即.
∴BD=5.4(米).
故答案为:5.4.
17.解:∵∠ADB=∠EDC,∠ABC=∠ECD=90°,
∴△ABD∽△ECD,
∴=,
∴AB===100(米).
故答案为:100.
三.解答题(共8小题,满分52分)
18.解:∵BD∥AE,
∴△CBD∽△CAE,
∴=,即=,
∴CB=4(m).
答:窗口底边离地面的高度BC是4m.
19.解:根据题意,易得△DCB∽△ACE,
∴CD:CE=BC:CA,
又因为AB=1.2米,CE=3.6米,BC=1.5米,
所以(3.6﹣ED):3.6=1.5:(1.2+1.5).
解得ED=1.6米.
20.解:∵AB∥CD,
∴△ABM∽△DCM,
∴===,(相似三角形对应高的比等于相似比),
∵MH∥AB,
∴△MDH∽△ADB,
∴==,
∴=,
解得MH=6.
答:点M离地面的高度MH为6m.
21.解:延长DC交AB于G,延长HC交AE于M,如图,
∵BC∥DH,
∴△BCG∽△HDC,
∴=,
而=,
∴=,解得BG=1.8,
∴CG==3,
∵身高是1.6米的小明站在坡面上,影子也都落在坡面上,长度为2米,
∴=,解得CM=2.56,
∵CM∥AG,
∴△ECM∽△EGA,
∴=,即=,解得AG=4.96,
∴AB=4.96+1.8=6.76(m).
答:树AB的高度为6.76m.
22.解:∵同一时刻物高与影长成正比,
∴EF:FG=OB:BC,即2.4:1.8=OB:36,
解得OB=48.
过O作OP垂直于DP,P为垂足.由题意得,P在圆O上,延长BA交DP延长线于Q.
∵同一时刻物高与影长成正比,
∴EF:FG=BQ:BD,即2.4:1.8=BQ:86,
解得BQ=,
∴OQ=BQ﹣OB=﹣48=.
在△QOP与△EGF中,
∠Q=∠GEF,∠OPQ=∠GFE,
∴△QOP∽△EGF,
∴OP:GF=OQ:EG,即OP:1.8=:3,
解得OP=40,
∴AB=OB+OA=48+40=88.
即摩天轮的半径为40m,最高点A的高为88m.
23.解:(1)∵PN∥BC,
∴△APN∽△ABC,
∴=,
∵QM=PN=x,MN=ED=y,AE=150﹣y,
∴,
∴y=150﹣x
∴S=xy=﹣x2+150x;
150﹣x>0,
解得:x<200,
则0<x<200;
(2)设矩形的面积为S,
则S=﹣x2+150x=﹣(x﹣100)2+7500.
故当x=100时,此时矩形的面积最大,最大面积为7500mm2.
24.解:如图由图可知,
∵BC∥ED,
∴△ABC∽△ADE,
∴,
又BC=10米,AF=3,FG=12米,
∴AG=AF+FG=15米
即,
∴DE=50,
50÷2=25,25+1=26,
答:DE处共有26棵树.
25.解:过A点作AN⊥CD,交EF于点M,
由题意得:AB=1.6m,EF=2.8m,BF=1.5m,BD=20m,EM=EF﹣AB=1.2m,AM=BF=1.5m,AN=BD=20m,
∵△AEM∽△ACN,
∴,
∴CN===16m.
∴CD=CN+ND=CN+AB=16+1.6=17.6m.
答:这幢楼的高度时17.6m.
一.选择题(共10小题,满分40分)
1.如图是装了液体的高脚杯示意图(数据如图)用去一部分液体后如右图所示,此时液面直径AB=( )
A.2cm B.2.5cm C.3cm D.4cm
2.一个直角三角形木架的两条直角边的边长分别是30cm,40cm.现要做一个与其相似的三角形木架,如果以60cm长的木条为其中一边,那么另两边中长度最大的一边最多可达到( )
A.60cm B.75cm C.100cm D.120cm
3.大约在两千四五百年前,如图1墨子和他的学生做了世界上第1个小孔成倒像的实验.并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.如图2所示的小孔成像实验中,若物距为10cm,像距为15cm,蜡烛火焰倒立的像的高度是6cm,则蜡烛火焰的高度是( )
A.3cm B.4cm C.6cm D.9cm
4.如图,在测量旗杆高度的数学活动中,某同学在脚下放了一面镜子,然后向后退,直到他刚好在镜子中看到旗杆的顶部.若眼睛距离地面AB=1.5m,同时量得BC=2m,CD=12m,则旗杆高度DE=( )
A.6m B.8m C.9m D.16m
5.如图,数学兴趣小组利用硬纸板自制的Rt△ABC来测量操场旗杆MN的高度,他们通过调整测量位置,并使边AC与旗杆顶点M在同一直线上,已知AC=0.8米,BC=0.5米,目测点A到地面的距离AD=1.5米,到旗杆的水平距离AE=20米,则旗杆MN的高度为( )
A.12米 B.12.5米 C.14米 D.15米
6.如图,为估算某河的宽度,在河对岸选定一个目标点A,在近岸取B,C,D三点,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上,若测得BE=20m,CE=10m,CD=20m,则河的宽度为( )
A.20m B.30m C.40m D.60m
7.《九章算术》是中国古代的数学专著,它奠定了中国古代数学的基本框架,以计算为中心,密切联系实际,以解决人们生产、生活中的数学问题为目的.书中记载了这样一个问题:“今有勾五步,股十二步,问勾中容方几何.”其大意是:如图,Rt△ABC的两条直角边的长分别为5和12,则它的内接正方形CDEF的边长为( )
A. B. C. D.
8.如图,一束平行的阳光从教室窗户射入,小兵同学量出BC=1m,NC=m,BN=m,AC=4.5m,MC=6m,则MA的长为( )
A.5m B.7.5m C.6m D.5.5m
9.如图是一块三角形钢材ABC,其中边BC=60cm,高AD=40cm,把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,则这个正方形零件的边长是( )
A.16 B.24 C.30 D.36
10.《九章算术》中,有一数学史上有名的测量问题:“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”今译如下:如图,矩形ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E,南门点F分别位于AB,AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH的长为( )
A.0.95里 B.1.05里 C.2.05里 D.2.15里
二.填空题(共7小题,满分28分)
11.小明身高是1.6m,影长为2m,同时刻教学楼的影长为24m,则楼的高是 .
12.在上午的某一时刻身高1.7米的小刚在地面上的投影长为3.4米,小明测得校园中旗杆在地面上的影子长16米,还有2米影子落在墙上,根据这些条件可以知道旗杆的高度为 米.
13.如图所示,D、E之间要挖建一条直线隧道,为计算隧道长度,工程人员在线段AD和AE上选择了测量点B,C,已知测得AD=100,AE=200,AB=40,AC=20,BC=30,则通过计算可得DE长为 .
14.如图,为测量小河两岸A、B两点之间的距离,在小河一侧选出一点C观测A、B两点,并使∠ACB=90°,若CD⊥AB,垂足为D,测得AD=10m,AC=24m,根据所测得的数据可算出A、B之间的距离是 .
15.我国古代数学发展源远流长,成就辉煌.著作《九章算术》中就有“井深几何”问题:“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”现在我们可以解释为:如图,矩形BCDE的边BE、CD表示井的直径,A在CB的延长线上,CD=5尺,AB=5尺,AD交BE于F,BF=0.4尺,根据以上条件,可求得井深BC为 尺.
16.如图,小杰同学跳起来把一个排球打在离他2米(即CO=2米)远的地上,排球反弹碰到墙上,如果他跳起击球时的高度是1.8米(即AC=1.8米),排球落地点离墙的距离是6米(即OD=6米),假设排球一直沿直线运动,那么排球能碰到墙面离地的高度BD的长是 米.
17.如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选定点B和C,使得AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,EC=50米,则两岸间的大致距离AB为 米.
三.解答题(共8小题,满分52分)
18.如图,阳光通过窗口照到室内,在地面上留下的亮区宽DE=2.7m,已知亮区一边到窗下的墙脚距离CE=8.7m,窗高AB=1.8m,那么窗口底边离地面的高度BC是多少?
19.如图,阳光通过窗口照到室内,在地面上留下一段亮区.已知亮区一边到窗下的墙脚距离CE=3.6m,窗高AB=1.2m,窗口底边离地面的高度BC=1.5m,求亮区ED的长.
20.如图,AB和CD表示两根直立于地面的柱子,AD和BC表示起固定作用的两根钢筋,AD与BC的交点为M,已知AB=10m,CD=15m,求点M离地面的高度MH.
21.如图,小明测得树AB落在水平地面上的影长BC为 2.4 米,落在坡面上的影长CE为3.2米,身高是1.6米的小明站在坡面上,影子也都落在坡面上,长度为2米.已知坡面的铅直高度CH与水平距离DH的比为3:4,试求树AB的高度.
22.同一时刻甲、乙两组同学在阳光下进行测量,甲组将一根长为2.4m的竹竿EF直立于平地,测得竹竿的影长FG为1.8m;摩天轮的立柱OB直立于平地,乙组测得立柱OB的影长BC为36m,摩天轮在立柱右侧影子的边缘D与立柱OB相距86m,求摩天轮的半径和最高点A的高.
23.如图,△ABC是一块锐角三角形材料,BC=200mm,高AD=150mm,要把它加工成一矩形零件,使矩形一边在BC上,其余两个顶点分别在AB、AC上.
(1)设PN=x,矩形PQMN的面积为S,求S关于x的函数表达式,并指出x的取值范围.
(2)当x为何值时,矩形PQMN的面积最大?最大值是多少?
24.如图,某校宣传栏BC后面12米处种有一排与宣传栏平行的若干棵树,即BC∥ED,且相邻两棵树的间隔为2米,一人站在距宣传栏前面的A处正好看到两端的树干,其余的树均被宣传栏挡住.已知AF⊥BC,AF=3米,BC=10米,求该宣传栏后DE处共有多少棵树?(不计宣传栏的厚度).
25.小明用如图所示的方式测量一幢楼高:线段AB、EF、CD分别表示人、竹、竿、楼房的高度,且A、C、E在一条直线上.测得人和竹竿的水平距离为1.5m,人和楼房的水平距离为20m,人的高度为1.6m,竹竿的高度为2.8m,求这幢楼的高度.
参考答案
一.选择题(共10小题,满分40分)
1.解:如图:过O作OM⊥CD,垂足为M,过O′作O′N⊥AB,垂足为N,
∵CD∥AB,
∴△CDO∽ABO′,即相似比为,
∴=,
∵OM=15﹣7=8(cm),O′N=11﹣7=4(cm),
∴=
∴AB=3(cm),
故选:C.
2.解:∵一个直角三角形木架的两条直角边的边长分别是30cm,40cm,
∴三角形的斜边长为:=50(cm),
∵现要做一个与其相似的三角形木架,以60cm长的木条为其中一边,
∴当另两边中长度最大的一边最长,则两三角形的相似比为:30:60=1:2,
故设要做的三角形最长边长为:50×2=100(cm).
故选:C.
3.解:设蜡烛火焰的高度是xcm,
由相似三角形的性质得到:=.
解得x=4.
即蜡烛火焰的高度是4cm.
故选:B.
4.解:∵AB⊥BD,DE⊥BD,
∴∠ABC=∠EDC=90°,
∵∠ACB=∠DCE,
∴△ABC∽△EDC,
∴=,
∴=,
∴DE=9(m),
故选:C.
5.解:∵∠CAB=∠EAM,∠ACB=∠AEM=90°,
∴△ACB∽△AEM,
∴=,
∴=,
∴EM=12.5(米),
∵四边形ADNE是矩形,
∴AD=EN=1.5(米),
∴MN=ME+EN=12.5+1.5=14(米).
故选:C.
6.解:∵AB⊥BC,CD⊥BC,
∴△BAE∽△CDE,
∴,
∵BE=20m,CE=10m,CD=20m,
∴,
解得:AB=40,
故选:C.
7.解:∵四边形CDEF是正方形,
∴CD=ED,DE∥CF,
设ED=x,则CD=x,AD=5﹣x,
∵DE∥CF,
∴∠ADE=∠C,∠AED=∠B,
∴△ADE∽△ACB,
∴=,
∴=,
∴x=,
∴正方形CDEF的边长为.
故选:B.
8.解:∵BN∥AM,
∴△BCN∽△ACM,
∴=,
∵BC=1m,BN=m,AC=4.5m,
∴=,
∴MA=7.5(m).
故选:B.
9.解:∵四边形EGHF为正方形,
∴BC∥EF,
∴△AEF∽△ABC;
设正方形零件的边长为x cm,则KD=EF=xcm,AK=(40﹣x)cm,
∵AD⊥BC,
∴=,
∴=,
解得:x=24.
即:正方形零件的边长为24cm.
故选:B.
10.解:EG⊥AB,FH⊥AD,HG经过A点,
∴FA∥EG,EA∥FH,
∴∠HFA=∠AEG=90°,∠FHA=∠EAG,
∴△GEA∽△AFH,
∴=,
∵AB=9里,DA=7里,EG=15里,
∴FA=3.5里,EA=4.5里,
∴=,
解得:FH=1.05里.
故选:B.
二.填空题(共7小题,满分28分)
11.解:设教学楼高度为xm,
列方程得:
解得x=19.2,
故教学楼的高度为19.2m.
故答案为:19.2m.
12.解:∵==,
∵CE=2,
∴CD=4,
∴BD=BC+CD=16+4=20米.
∴AB=BD=×20=10米.
故应填10.
13.解:∵AD=100,AE=200,AB=40,AC=20,
∴==,==,
∴=,
而∠BAC=∠EAD,
∴△ABC∽△EAD,
∴=,
∴DE=5BC=5×30=150.
故答案为150.
14.解:∵∠ACB=90°、CD⊥AB,
∴∠ACB=∠ADC=90°,
∴∠A+∠B=∠A+∠ACD=90°,
则∠B=∠ACD,
∴△ACD∽△ABC,
∴=,即=,
解得:AB=57.6(m),
故答案为:57.6.
15.解:设BC=x尺.
∵四边形BCDE是矩形,
∴BF∥CD,
∴△AFB∽△ADC,
∴=,
∴=,
解得x=57.5,
经检验:x=57.5是分式方程的解.
∴BC=57.5(尺).
故答案为:57.5.
16.解:由题意得:∠AOC=∠BOD.
∵AC⊥CD,BD⊥CD,
∴∠ACO=∠BDO=90°.
∴△ACO∽△BDO.
∴.
即.
∴BD=5.4(米).
故答案为:5.4.
17.解:∵∠ADB=∠EDC,∠ABC=∠ECD=90°,
∴△ABD∽△ECD,
∴=,
∴AB===100(米).
故答案为:100.
三.解答题(共8小题,满分52分)
18.解:∵BD∥AE,
∴△CBD∽△CAE,
∴=,即=,
∴CB=4(m).
答:窗口底边离地面的高度BC是4m.
19.解:根据题意,易得△DCB∽△ACE,
∴CD:CE=BC:CA,
又因为AB=1.2米,CE=3.6米,BC=1.5米,
所以(3.6﹣ED):3.6=1.5:(1.2+1.5).
解得ED=1.6米.
20.解:∵AB∥CD,
∴△ABM∽△DCM,
∴===,(相似三角形对应高的比等于相似比),
∵MH∥AB,
∴△MDH∽△ADB,
∴==,
∴=,
解得MH=6.
答:点M离地面的高度MH为6m.
21.解:延长DC交AB于G,延长HC交AE于M,如图,
∵BC∥DH,
∴△BCG∽△HDC,
∴=,
而=,
∴=,解得BG=1.8,
∴CG==3,
∵身高是1.6米的小明站在坡面上,影子也都落在坡面上,长度为2米,
∴=,解得CM=2.56,
∵CM∥AG,
∴△ECM∽△EGA,
∴=,即=,解得AG=4.96,
∴AB=4.96+1.8=6.76(m).
答:树AB的高度为6.76m.
22.解:∵同一时刻物高与影长成正比,
∴EF:FG=OB:BC,即2.4:1.8=OB:36,
解得OB=48.
过O作OP垂直于DP,P为垂足.由题意得,P在圆O上,延长BA交DP延长线于Q.
∵同一时刻物高与影长成正比,
∴EF:FG=BQ:BD,即2.4:1.8=BQ:86,
解得BQ=,
∴OQ=BQ﹣OB=﹣48=.
在△QOP与△EGF中,
∠Q=∠GEF,∠OPQ=∠GFE,
∴△QOP∽△EGF,
∴OP:GF=OQ:EG,即OP:1.8=:3,
解得OP=40,
∴AB=OB+OA=48+40=88.
即摩天轮的半径为40m,最高点A的高为88m.
23.解:(1)∵PN∥BC,
∴△APN∽△ABC,
∴=,
∵QM=PN=x,MN=ED=y,AE=150﹣y,
∴,
∴y=150﹣x
∴S=xy=﹣x2+150x;
150﹣x>0,
解得:x<200,
则0<x<200;
(2)设矩形的面积为S,
则S=﹣x2+150x=﹣(x﹣100)2+7500.
故当x=100时,此时矩形的面积最大,最大面积为7500mm2.
24.解:如图由图可知,
∵BC∥ED,
∴△ABC∽△ADE,
∴,
又BC=10米,AF=3,FG=12米,
∴AG=AF+FG=15米
即,
∴DE=50,
50÷2=25,25+1=26,
答:DE处共有26棵树.
25.解:过A点作AN⊥CD,交EF于点M,
由题意得:AB=1.6m,EF=2.8m,BF=1.5m,BD=20m,EM=EF﹣AB=1.2m,AM=BF=1.5m,AN=BD=20m,
∵△AEM∽△ACN,
∴,
∴CN===16m.
∴CD=CN+ND=CN+AB=16+1.6=17.6m.
答:这幢楼的高度时17.6m.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
