25.5相似三角形的性质同步达标测评 2021-2022学年冀教版九年级数学上册(Word版 含答案)
文档属性
| 名称 | 25.5相似三角形的性质同步达标测评 2021-2022学年冀教版九年级数学上册(Word版 含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 568.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-14 11:27:12 | ||
图片预览


文档简介
2021-2022学年冀教版九年级数学上册《25.5相似三角形的性质》同步达标测评(附答案)
一.选择题(共14小题,满分42分)
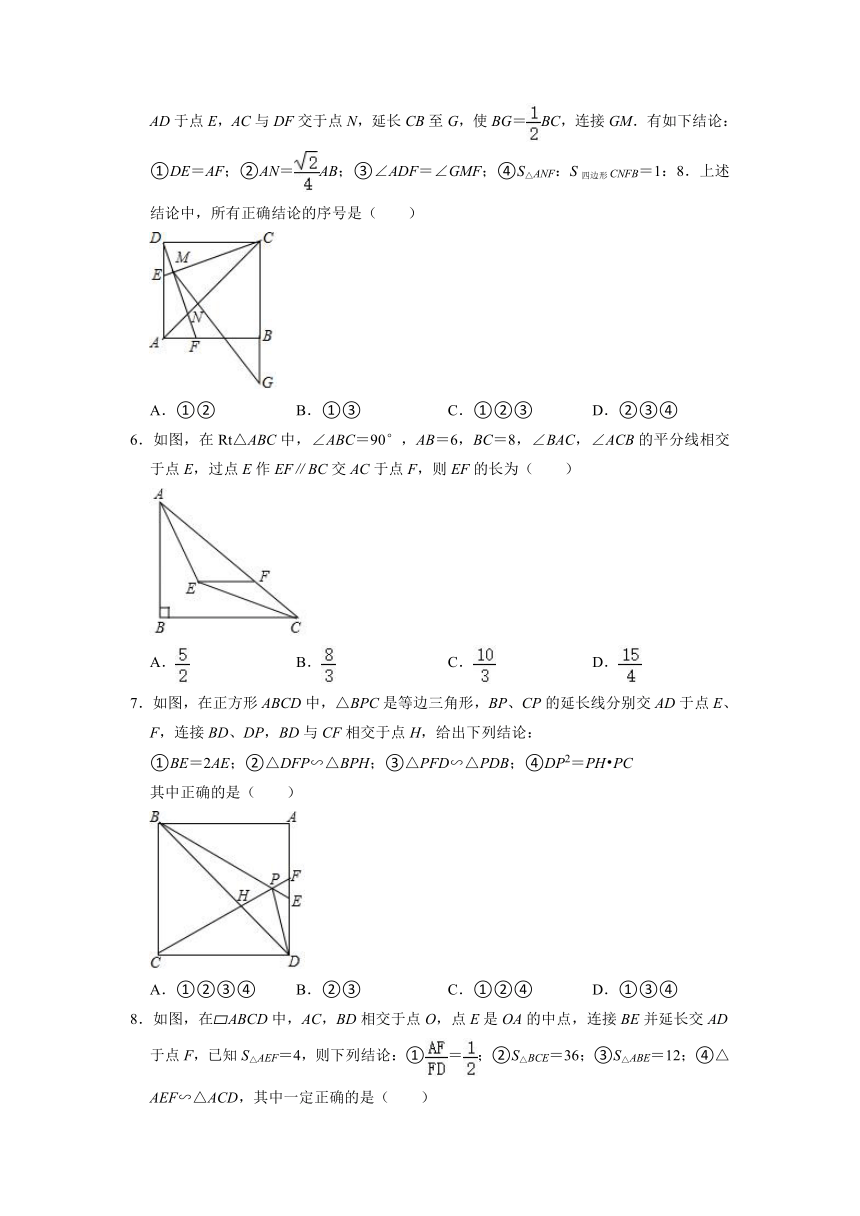
1.如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,则S△DOE:S△AOC的值为( )
,
A. B. C. D.
2.如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
A.3:4 B.9:16 C.9:1 D.3:1
3.如图,在平行四边形ABCD中,E为CD上一点,连接AE、BE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )
A.2:3 B.2:5 C.3:5 D.3:2
4.如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=10,BC=16,则线段EF的长为( )
A.2 B.3 C.4 D.5
5.如图,正方形ABCD,点F在边AB上,且AF:FB=1:2,CE⊥DF,垂足为M,且交AD于点E,AC与DF交于点N,延长CB至G,使BG=BC,连接GM.有如下结论:①DE=AF;②AN=AB;③∠ADF=∠GMF;④S△ANF:S四边形CNFB=1:8.上述结论中,所有正确结论的序号是( )
A.①② B.①③ C.①②③ D.②③④
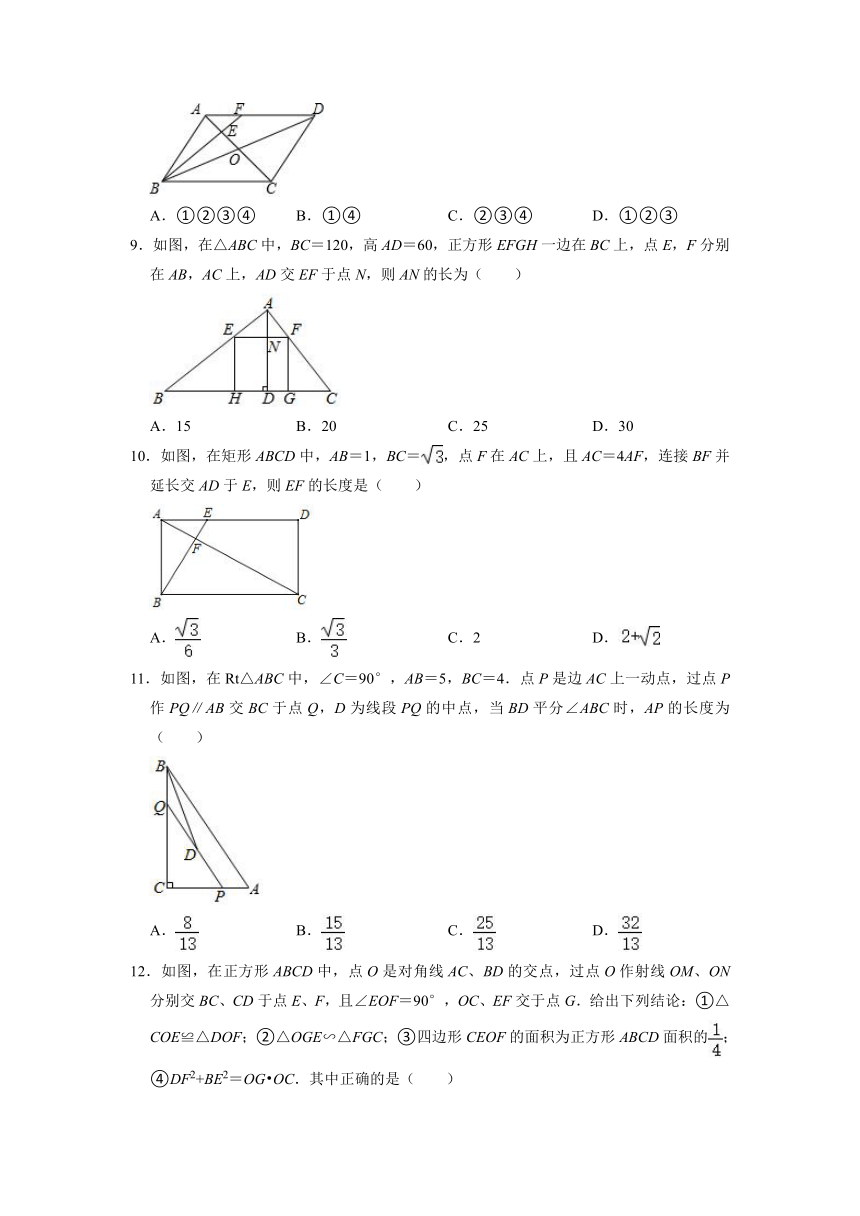
6.如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,∠BAC,∠ACB的平分线相交于点E,过点E作EF∥BC交AC于点F,则EF的长为( )
A. B. C. D.
7.如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:
①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PH PC
其中正确的是( )
A.①②③④ B.②③ C.①②④ D.①③④
8.如图,在 ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①=;②S△BCE=36;③S△ABE=12;④△AEF∽△ACD,其中一定正确的是( )
A.①②③④ B.①④ C.②③④ D.①②③
9.如图,在△ABC中,BC=120,高AD=60,正方形EFGH一边在BC上,点E,F分别在AB,AC上,AD交EF于点N,则AN的长为( )
A.15 B.20 C.25 D.30
10.如图,在矩形ABCD中,AB=1,BC=,点F在AC上,且AC=4AF,连接BF并延长交AD于E,则EF的长度是( )
A. B. C.2 D.
11.如图,在Rt△ABC中,∠C=90°,AB=5,BC=4.点P是边AC上一动点,过点P作PQ∥AB交BC于点Q,D为线段PQ的中点,当BD平分∠ABC时,AP的长度为( )
A. B. C. D.
12.如图,在正方形ABCD中,点O是对角线AC、BD的交点,过点O作射线OM、ON分别交BC、CD于点E、F,且∠EOF=90°,OC、EF交于点G.给出下列结论:①△COE≌△DOF;②△OGE∽△FGC;③四边形CEOF的面积为正方形ABCD面积的;④DF2+BE2=OG OC.其中正确的是( )
A.①②③④ B.①②③ C.①②④ D.③④
13.如图,正方形ABCD中,E,F分别在边AD,CD上,AF,BE相交于点G,若AE=3ED,DF=CF,则的值是( )
A. B. C. D.
14.如图所示,已知:点A(0,0),,C(0,1).在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,则第n个等边三角形的边长等于( )
A. B. C. D.
二.填空题(共5小题,满分20分)
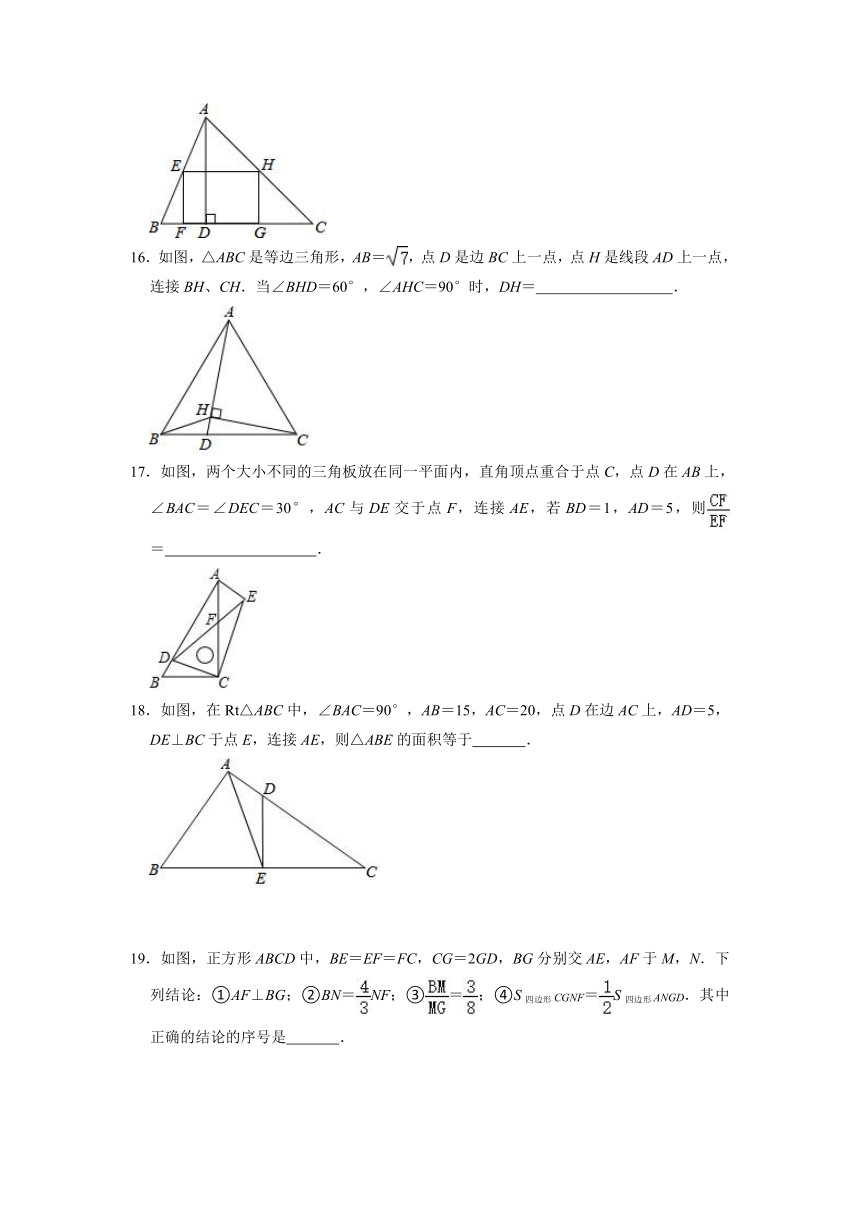
15.如图,矩形EFGH内接于△ABC,且边FG落在BC上.若BC=3,AD=2,EF=EH,AD⊥BC,那么EH的长为 .
16.如图,△ABC是等边三角形,AB=,点D是边BC上一点,点H是线段AD上一点,连接BH、CH.当∠BHD=60°,∠AHC=90°时,DH= .
17.如图,两个大小不同的三角板放在同一平面内,直角顶点重合于点C,点D在AB上,
∠BAC=∠DEC=30°,AC与DE交于点F,连接AE,若BD=1,AD=5,则= .
18.如图,在Rt△ABC中,∠BAC=90°,AB=15,AC=20,点D在边AC上,AD=5,DE⊥BC于点E,连接AE,则△ABE的面积等于 .
19.如图,正方形ABCD中,BE=EF=FC,CG=2GD,BG分别交AE,AF于M,N.下列结论:①AF⊥BG;②BN=NF;③=;④S四边形CGNF=S四边形ANGD.其中正确的结论的序号是 .
三.解答题(共5小题,满分58分)
20.如图,在△ABP中,C,D分别是AP,BP上的点.若CD=CP=4,DP=5,AC=3.5,BD=1.
(1)求证:△ABP∽△DCP;
(2)求AB的长.
21.如图,AB⊥BC,DC⊥BC,E是BC上一点,使得AE⊥DE.
(1)求证:△ABE∽△ECD;
(2)若AB=4,AE=BC=5,求CD的长.
22.已知:如图,△ABC中,AB=4,BC=8,D为BC边上一点,BD=2.
求证:∠BDA=∠BAC.
23.在锐角△ABC中,点D,E分别在AC、AB上,AG⊥BC与点G,AF⊥DE于F,∠EAF=∠GAC.
(1)求证:△AEF∽△ACG.
(2)求证:∠ADE=∠B.
(3)若AD=3,AB=5,求.
24.如图,菱形ABCD的边长为20cm,∠ABC=120°.动点P、Q同时从点A出发,其中P以4cm/s的速度,沿A→B→C的路线向点C运动;Q以2cm/s的速度,沿A→C的路线向点C运动.当P、Q到达终点C时,整个运动随之结束,设运动时间为t秒.
(1)在点P、Q运动过程中,请判断PQ与对角线AC的位置关系,并说明理由;
(2)若点Q关于菱形ABCD的对角线交点O的对称点为M,过点P且垂直于AB的直线l交菱形ABCD的边AD(或CD)于点N.
①当t为何值时,点P、M、N在一直线上?
②当点P、M、N不在一直线上时,是否存在这样的t,使得△PMN是以PN为一直角边的直角三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
参考答案
一.选择题(共14小题,满分42分)
1.解:∵S△BDE:S△CDE=1:3,
∴BE:EC=1:3;
∴BE:BC=1:4;
∵DE∥AC,
∴△DOE∽△AOC,
∴=,
∴S△DOE:S△AOC==,
故选:D.
2.解:∵四边形ABCD为平行四边形,
∴DC∥AB,
∴△DFE∽△BFA,
∵DE:EC=3:1,
∴DE:DC=3:4,
∴DE:AB=3:4,
∴S△DFE:S△BFA=9:16.
故选:B.
3.解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠EAB=∠DEF,∠AFB=∠DFE,
∴△DEF∽△BAF,
∵S△DEF:S△ABF=4:25,
∴=,
∵AB=CD,
∴DE:EC=2:3.
故选:A.
4.解:∵AF⊥BF,
∴∠AFB=90°,
∵AB=10,D为AB中点,
∴DF=AB=AD=BD=5,
∴∠ABF=∠BFD,
又∵BF平分∠ABC,
∴∠ABF=∠CBF,
∴∠CBF=∠DFB,
∴DE∥BC,
∴△ADE∽△ABC,
∴=,即,
解得:DE=8,
∴EF=DE﹣DF=3,
故选:B.
5.解:∵四边形ABCD是正方形,
∴AD=AB=CD=BC,∠CDE=∠DAF=90°,
∵CE⊥DF,
∴∠DCE+∠CDF=∠ADF+∠CDF=90°,
∴∠ADF=∠DCE,
在△ADF与△DCE中,
,
∴△ADF≌△DCE(ASA),
∴DE=AF;故①正确;
∵AB∥CD,
∴=,
∵AF:FB=1:2,
∴AF:AB=AF:CD=1:3,
∴=,
∴=,
∵AC=AB,
∴=,
∴AN=AB;故②正确;
作GH⊥CE于H,设AF=DE=a,BF=2a,则AB=CD=BC=3a,EC=a,
由△CMD∽△CDE,可得CM=a,
由△GHC∽△CDE,可得CH=a,
∴CH=MH=CM,
∵GH⊥CM,
∴GM=GC,
∴∠GMH=∠GCH,
∵∠FMG+∠GMH=90°,∠DCE+∠GCM=90°,
∴∠FMG=∠DCE,
∵∠ADF=∠DCE,
∴∠ADF=∠GMF;故③正确,
(补充方法:延长MF交CG的延长线于T,证明CG=GT,利用直角三角形斜边中线的性质即可解决问题)
设△ANF的面积为m,
∵AF∥CD,
∴==,△AFN∽△CDN,
∴△ADN的面积为3m,△DCN的面积为9m,
∴△ADC的面积=△ABC的面积=12m,
∴S△ANF:S四边形CNFB=1:11,故④错误,
故选:C.
6.解:如图,延长FE交AB于点D,作EG⊥BC于点G,作EH⊥AC于点H,
∵EF∥BC、∠ABC=90°,
∴FD⊥AB,
∵EG⊥BC,
∴四边形BDEG是矩形,
∵AE平分∠BAC、CE平分∠ACB,
∴ED=EH=EG,∠DAE=∠HAE,
∴四边形BDEG是正方形,
在△DAE和△HAE中,
∵,
∴△DAE≌△HAE(AAS),
∴AD=AH,
同理△CGE≌△CHE,
∴CG=CH,
设BD=BG=x,则AD=AH=6﹣x、CG=CH=8﹣x,
∵AC===10,
∴6﹣x+8﹣x=10,
解得:x=2,
∴BD=DE=2,AD=4,
∵DF∥BC,
∴△ADF∽△ABC,
∴=,即=,
解得:DF=,
则EF=DF﹣DE=﹣2=,
故选:C.
7.解:∵△BPC是等边三角形,
∴BP=PC=BC,∠PBC=∠PCB=∠BPC=60°,
在正方形ABCD中,
∵AB=BC=CD,∠A=∠ADC=∠BCD=90°
∴∠ABE=∠DCF=30°,
∴BE=2AE;故①正确;
∵PC=CD,∠PCD=30°,
∴∠PDC=75°,
∴∠FDP=15°,
∵∠DBA=45°,
∴∠PBD=15°,
∴∠FDP=∠PBD,
∵∠DFP=∠BPC=60°,
∴△DFP∽△BPH;故②正确;
∵∠FDP=∠PBD=15°,∠ADB=45°,
∴∠PDB=30°,而∠DFP=60°,
∴∠PFD≠∠PDB,
∴△PFD与△PDB不会相似;故③错误;
∵∠PDH=∠PCD=30°,∠DPH=∠DPC,
∴△DPH∽△CPD,
∴,
∴DP2=PH PC,故④正确;
故选:C.
8.解:∵在 ABCD中,AO=AC,
∵点E是OA的中点,
∴AE=CE,
∵AD∥BC,
∴△AFE∽△CBE,
∴==,
∵AD=BC,
∴AF=AD,
∴=;故①正确;
∵S△AEF=4,=()2=,
∴S△BCE=36;故②正确;
∵==,
∴=,
∴S△ABE=12,故③正确;
∵BF不平行于CD,
∴△AEF与△ADC只有一个角相等,
∴△AEF与△ACD不一定相似,故④错误,
故选:D.
9.解:设正方形EFGH的边长EF=EH=x,
∵四边形EFGH是正方形,
∴∠HEF=∠EHG=90°,EF∥BC,
∴△AEF∽△ABC,
∵AD是△ABC的高,
∴∠HDN=90°,
∴四边形EHDN是矩形,
∴DN=EH=x,
∵△AEF∽△ABC,
∴=(相似三角形对应边上的高的比等于相似比),
∵BC=120,AD=60,
∴AN=60﹣x,
∴=,
解得:x=40,
∴AN=60﹣x=60﹣40=20.
故选:B.
10.解:在矩形ABCD中,AB=1,BC=,AD∥BC,
∴AC=2,
∵AC=4AF,
∴AF=,CF=,
∵AD∥BC,
∴==,
∴AE=,
∴BE=,
∴EF=BE=.
故选:A.
11.解:∵∠C=90°,AB=5,BC=4,
∴AC==3,
∵PQ∥AB,
∴∠ABD=∠BDQ,又∠ABD=∠QBD,
∴∠QBD=∠BDQ,
∴QB=QD,
∴QP=2QB,
∵PQ∥AB,
∴△CPQ∽△CAB,
∴==,即==,
解得,CP=,
∴AP=CA﹣CP=,
故选:B.
12.解:①∵四边形ABCD是正方形,
∴OC=OD,AC⊥BD,∠ODF=∠OCE=45°,
∵∠MON=90°,
∴∠COM=∠DOF,
∴△COE≌△DOF(ASA),
故①正确;
②∵△COE≌△DOF,
∴OE=OF,
∵∠MON=90°,
∴∠OEG=45°=∠FCG,
∵∠OGE=∠FGC,
∴△OGE∽△FGC,
故②正确;
③∵△COE≌△DOF,
∴S△COE=S△DOF,
∴,
故③正确;
④∵△COE≌△DOF,
∴OE=OF,
又∵∠EOF=90°,
∴△EOF是等腰直角三角形,
∴∠OEG=45°=∠OCE,
∵∠EOG=∠COE,
∴△OEG∽△OCE,
∴OE:OC=OG:OE,
∴OG OC=OE2,
∵OC=AC,OE=EF,
∴OG AC=EF2,
∵CE=DF,BC=CD,
∴BE=CF,
又∵Rt△CEF中,CF2+CE2=EF2,
∴BE2+DF2=EF2,
∴OG AC=BE2+DF2,
故④错误,
故选:B.
13.解:如图,作FN∥AD,交AB于N,交BE于M.
∵四边形ABCD是正方形,
∴AB∥CD,∵FN∥AD,
∴四边形ANFD是平行四边形,
∵∠D=90°,
∴四边形ANFD是矩形,
∵AE=3DE,设DE=a,则AE=3a,AD=AB=CD=FN=4a,AN=DF=2a,
∵AN=BN,MN∥AE,
∴BM=ME,
∴MN=a,
∴FM=a,
∵AE∥FM,
∴===,
故选:C.
14.解:如图,过A1作A1D⊥BO于点D.
设AD=DB1=x
则由△BA1D∽△BCO得:
=
解得x=
所以A2B1B2的边长为.
同理解得边长依次为,…
所以第n个等边三角形的边长等于.
故选:A.
二.填空题(共5小题,满分20分)
15.解:∵四边形EFGH是矩形,
∴EH∥BC,
∴△AEH∽△ABC,
∵AM⊥EH,AD⊥BC,
∴=,
设EH=3x,则有EF=2x,AM=AD﹣EF=2﹣2x,
∴=,
解得:x=,
则EH=.
故答案为:.
16.解:作AE⊥BH于E,BF⊥AH于F,如图,
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∵∠BHD=∠ABH+∠BAH=60°,∠BAH+∠CAH=60°,
∴∠ABH=∠CAH,
在△ABE和△CAH中
,
∴△ABE≌△CAH,
∴BE=AH,AE=CH,
在Rt△AHE中,∠AHE=∠BHD=60°,
∴sin∠AHE=,HE=AH,
∴AE=AH sin60°=AH,
∴CH=AH,
在Rt△AHC中,AH2+(AH)2=AC2=()2,解得AH=2,
∴BE=2,HE=1,AE=CH=,
∴BH=BE﹣HE=2﹣1=1,
在Rt△BFH中,HF=BH=,BF=,
∵BF∥CH,
∴△CHD∽△BFD,
∴===2,
∴DH=HF=×=.
故答案为.
17.解:如图,过点C作CM⊥DE于点M,过点E作EN⊥AC于点N,
∵BD=1,AD=5,
∴AB=BD+AD=6,
∵在Rt△ABC中,∠BAC=30°,∠B=90°﹣∠BAC=60°,
∴BC=AB=3,AC=BC=3,
在Rt△BCA与Rt△DCE中,
∵∠BAC=∠DEC=30°,
∴tan∠BAC=tan∠DEC,
∴,
∵∠BCA=∠DCE=90°,
∴∠BCA﹣∠DCA=∠DCE﹣∠DCA,
∴∠BCD=∠ACE,
∴△BCD∽△ACE,
∴∠CAE=∠B=60°,,
∴∠DAE=∠DAC+∠CAE=30°+60°=90°,,
∴AE=,
在Rt△ADE中,
DE===2,
在Rt△DCE中,∠DEC=30°,
∴∠EDC=60°,DC=DE=,
在Rt△DCM中,
MC=DC=,
在Rt△AEN中,
NE=AE=,
∵∠MFC=∠NFE,∠FMC=∠FNE=90°,
∴△MFC∽△NFE,
∴===,
方法二:求出AE后,证明△DFC∽△AFE,利用相似三角形的性质求解即可.
故答案为:.
18.解:∵在Rt△ABC中,∠BAC=90°,AB=15,AC=20,
∴BC==25,△ABC的面积=AB AC=×15×20=150,
∵AD=5,
∴CD=AC﹣AD=15,
∵DE⊥BC,
∴∠DEC=∠BAC=90°,
又∵∠C=∠C,
∴△CDE∽△CBA,
∴,即,
解得:CE=12,
∴BE=BC﹣CE=13,
∵△ABE的面积:△ABC的面积=BE:BC=13:25,
∴△ABE的面积=×150=78;
故答案为:78.
19.解:①∵四边形ABCD为正方形,
∴AB=BC=CD,
∵BE=EF=FC,CG=2GD,
∴BF=CG,
∵在△ABF和△BCG中,,
∴△ABF≌△BCG,
∴∠BAF=∠CBG,
∵∠BAF+∠BFA=90°,
∴∠CBG+∠BFA=90°,即AF⊥BG;①正确;
②∵在△BNF和△BCG中,,
∴△BNF∽△BCG,∴==,
∴BN=NF;②错误;
③作EH⊥AF,令AB=3,则BF=2,BE=EF=CF=1,
AF==,
∵S△ABF=AF BN=AB BF,
∴BN=,NF=BN=,
∴AN=AF﹣NF=,
∵E是BF中点,
∴EH是△BFN的中位线,
∴EH=,NH=,BN∥EH,
∴AH=,=,解得:MN=,
∴BM=BN﹣MN=,MG=BG﹣BM=,
∴=;③正确;
④连接AG,FG,根据③中结论,
则NG=BG﹣BN=,
∵S四边形CGNF=S△CFG+S△GNF=CG CF+NF NG=1+=,
S四边形ANGD=S△ANG+S△ADG=AN GN+AD DG=+=,
∴S四边形CGNF≠S四边形ANGD,④错误;
故答案为 ①③.
三.解答题(共5小题,满分58分)
20.解:(1)证明:∵CD=CP=4,DP=5,AC=3.5,BD=1,
∴AP=AC+CP=3.5+4=7.5,BP=BD+DP=1+5=6,
∴=,==,
∴,
∵∠DPC=∠APB,
∴△ABP∽△DCP;
(2)∵△ABP∽△DCP,
∴,
即:=,
∴AB=6.
21.解:(1)证明:如图,
∵AE⊥DE,
∴∠AED=90°,
∴∠AEB+∠DEC=90°,
∵AB⊥BC,DC⊥BC,
∴∠B+∠C=90°,
∴∠BAE=∠CED,
∴△ABE∽△ECD;
(2)在Rt△ABE中,由勾股定理得BE=3,
∴EC=BC﹣BE=2,
由(1)得△ABE∽△ECD,
∴,即,
解得CD=.
22.证明:在△ABC中,AB=4,BC=8,BD=2.
∴,,
∴,
又∵∠ABD=∠CBA,
∴△ABD∽△CBA,
∴∠BDA=∠BAC.
23.证明:(1)∵AG⊥BC,AF⊥DE于,
∴∠AFE=∠AGC=90°.
∵∠EAF=∠GAC
∴△AEF∽△ACG.
(2)由(1)知△AEF∽△ACG,
∴∠AEF=∠C
∵∠DAE=∠BAC(公共角),
∴△EAD∽△CAB.
∴∠ADE=∠B.
解:(3)由(2)知:△ADE∽△ABC,
∴.
由(1)知△AEF∽△ACG,
∴.
∴.
∵AD=3,AB=5,
∴.
24.解:(1)若0<t≤5,则AP=4t,AQ=2t.
则==,
又∵AO=10,AB=20,
∴==.
∴=.
又∵∠CAB=30°,
∴△APQ∽△ABO.
∴∠AQP=90°,即PQ⊥AC.
当5<t<10时,同理,可由△PCQ∽△BCO得∠PQC=90°,即PQ⊥AC.
∴在点P、Q运动过程中,始终有PQ⊥AC.
(2)①如图,在Rt△APM中,
∵∠PAM=30°,AP=4t,
∴AM=.
在△APQ中,∠AQP=90°,
∴AQ=2t,
∴QM=AC﹣2AQ=20﹣4t.
由AQ+QM=AM得:2t+20﹣4t=,
解得t=.
∴当t=时,点P、M、N在一直线上.
②存在这样的t,使△PMN是以PN为一直角边的直角三角形.
设l交AC于H.
如图1,当点N在AD上时,若PN⊥MN,则∠NMH=30°.
∴MH=2NH.得20﹣4t﹣=2×,解得t=2.
如图2,当点N在CD上时,若PM⊥PN,则∠HMP=30°.
∴MH=2PH,同理可得t=.
故当t=2或时,存在以PN为一直角边的直角三角形.
一.选择题(共14小题,满分42分)
1.如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,则S△DOE:S△AOC的值为( )
,
A. B. C. D.
2.如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
A.3:4 B.9:16 C.9:1 D.3:1
3.如图,在平行四边形ABCD中,E为CD上一点,连接AE、BE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )
A.2:3 B.2:5 C.3:5 D.3:2
4.如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=10,BC=16,则线段EF的长为( )
A.2 B.3 C.4 D.5
5.如图,正方形ABCD,点F在边AB上,且AF:FB=1:2,CE⊥DF,垂足为M,且交AD于点E,AC与DF交于点N,延长CB至G,使BG=BC,连接GM.有如下结论:①DE=AF;②AN=AB;③∠ADF=∠GMF;④S△ANF:S四边形CNFB=1:8.上述结论中,所有正确结论的序号是( )
A.①② B.①③ C.①②③ D.②③④
6.如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,∠BAC,∠ACB的平分线相交于点E,过点E作EF∥BC交AC于点F,则EF的长为( )
A. B. C. D.
7.如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:
①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PH PC
其中正确的是( )
A.①②③④ B.②③ C.①②④ D.①③④
8.如图,在 ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①=;②S△BCE=36;③S△ABE=12;④△AEF∽△ACD,其中一定正确的是( )
A.①②③④ B.①④ C.②③④ D.①②③
9.如图,在△ABC中,BC=120,高AD=60,正方形EFGH一边在BC上,点E,F分别在AB,AC上,AD交EF于点N,则AN的长为( )
A.15 B.20 C.25 D.30
10.如图,在矩形ABCD中,AB=1,BC=,点F在AC上,且AC=4AF,连接BF并延长交AD于E,则EF的长度是( )
A. B. C.2 D.
11.如图,在Rt△ABC中,∠C=90°,AB=5,BC=4.点P是边AC上一动点,过点P作PQ∥AB交BC于点Q,D为线段PQ的中点,当BD平分∠ABC时,AP的长度为( )
A. B. C. D.
12.如图,在正方形ABCD中,点O是对角线AC、BD的交点,过点O作射线OM、ON分别交BC、CD于点E、F,且∠EOF=90°,OC、EF交于点G.给出下列结论:①△COE≌△DOF;②△OGE∽△FGC;③四边形CEOF的面积为正方形ABCD面积的;④DF2+BE2=OG OC.其中正确的是( )
A.①②③④ B.①②③ C.①②④ D.③④
13.如图,正方形ABCD中,E,F分别在边AD,CD上,AF,BE相交于点G,若AE=3ED,DF=CF,则的值是( )
A. B. C. D.
14.如图所示,已知:点A(0,0),,C(0,1).在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,则第n个等边三角形的边长等于( )
A. B. C. D.
二.填空题(共5小题,满分20分)
15.如图,矩形EFGH内接于△ABC,且边FG落在BC上.若BC=3,AD=2,EF=EH,AD⊥BC,那么EH的长为 .
16.如图,△ABC是等边三角形,AB=,点D是边BC上一点,点H是线段AD上一点,连接BH、CH.当∠BHD=60°,∠AHC=90°时,DH= .
17.如图,两个大小不同的三角板放在同一平面内,直角顶点重合于点C,点D在AB上,
∠BAC=∠DEC=30°,AC与DE交于点F,连接AE,若BD=1,AD=5,则= .
18.如图,在Rt△ABC中,∠BAC=90°,AB=15,AC=20,点D在边AC上,AD=5,DE⊥BC于点E,连接AE,则△ABE的面积等于 .
19.如图,正方形ABCD中,BE=EF=FC,CG=2GD,BG分别交AE,AF于M,N.下列结论:①AF⊥BG;②BN=NF;③=;④S四边形CGNF=S四边形ANGD.其中正确的结论的序号是 .
三.解答题(共5小题,满分58分)
20.如图,在△ABP中,C,D分别是AP,BP上的点.若CD=CP=4,DP=5,AC=3.5,BD=1.
(1)求证:△ABP∽△DCP;
(2)求AB的长.
21.如图,AB⊥BC,DC⊥BC,E是BC上一点,使得AE⊥DE.
(1)求证:△ABE∽△ECD;
(2)若AB=4,AE=BC=5,求CD的长.
22.已知:如图,△ABC中,AB=4,BC=8,D为BC边上一点,BD=2.
求证:∠BDA=∠BAC.
23.在锐角△ABC中,点D,E分别在AC、AB上,AG⊥BC与点G,AF⊥DE于F,∠EAF=∠GAC.
(1)求证:△AEF∽△ACG.
(2)求证:∠ADE=∠B.
(3)若AD=3,AB=5,求.
24.如图,菱形ABCD的边长为20cm,∠ABC=120°.动点P、Q同时从点A出发,其中P以4cm/s的速度,沿A→B→C的路线向点C运动;Q以2cm/s的速度,沿A→C的路线向点C运动.当P、Q到达终点C时,整个运动随之结束,设运动时间为t秒.
(1)在点P、Q运动过程中,请判断PQ与对角线AC的位置关系,并说明理由;
(2)若点Q关于菱形ABCD的对角线交点O的对称点为M,过点P且垂直于AB的直线l交菱形ABCD的边AD(或CD)于点N.
①当t为何值时,点P、M、N在一直线上?
②当点P、M、N不在一直线上时,是否存在这样的t,使得△PMN是以PN为一直角边的直角三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
参考答案
一.选择题(共14小题,满分42分)
1.解:∵S△BDE:S△CDE=1:3,
∴BE:EC=1:3;
∴BE:BC=1:4;
∵DE∥AC,
∴△DOE∽△AOC,
∴=,
∴S△DOE:S△AOC==,
故选:D.
2.解:∵四边形ABCD为平行四边形,
∴DC∥AB,
∴△DFE∽△BFA,
∵DE:EC=3:1,
∴DE:DC=3:4,
∴DE:AB=3:4,
∴S△DFE:S△BFA=9:16.
故选:B.
3.解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠EAB=∠DEF,∠AFB=∠DFE,
∴△DEF∽△BAF,
∵S△DEF:S△ABF=4:25,
∴=,
∵AB=CD,
∴DE:EC=2:3.
故选:A.
4.解:∵AF⊥BF,
∴∠AFB=90°,
∵AB=10,D为AB中点,
∴DF=AB=AD=BD=5,
∴∠ABF=∠BFD,
又∵BF平分∠ABC,
∴∠ABF=∠CBF,
∴∠CBF=∠DFB,
∴DE∥BC,
∴△ADE∽△ABC,
∴=,即,
解得:DE=8,
∴EF=DE﹣DF=3,
故选:B.
5.解:∵四边形ABCD是正方形,
∴AD=AB=CD=BC,∠CDE=∠DAF=90°,
∵CE⊥DF,
∴∠DCE+∠CDF=∠ADF+∠CDF=90°,
∴∠ADF=∠DCE,
在△ADF与△DCE中,
,
∴△ADF≌△DCE(ASA),
∴DE=AF;故①正确;
∵AB∥CD,
∴=,
∵AF:FB=1:2,
∴AF:AB=AF:CD=1:3,
∴=,
∴=,
∵AC=AB,
∴=,
∴AN=AB;故②正确;
作GH⊥CE于H,设AF=DE=a,BF=2a,则AB=CD=BC=3a,EC=a,
由△CMD∽△CDE,可得CM=a,
由△GHC∽△CDE,可得CH=a,
∴CH=MH=CM,
∵GH⊥CM,
∴GM=GC,
∴∠GMH=∠GCH,
∵∠FMG+∠GMH=90°,∠DCE+∠GCM=90°,
∴∠FMG=∠DCE,
∵∠ADF=∠DCE,
∴∠ADF=∠GMF;故③正确,
(补充方法:延长MF交CG的延长线于T,证明CG=GT,利用直角三角形斜边中线的性质即可解决问题)
设△ANF的面积为m,
∵AF∥CD,
∴==,△AFN∽△CDN,
∴△ADN的面积为3m,△DCN的面积为9m,
∴△ADC的面积=△ABC的面积=12m,
∴S△ANF:S四边形CNFB=1:11,故④错误,
故选:C.
6.解:如图,延长FE交AB于点D,作EG⊥BC于点G,作EH⊥AC于点H,
∵EF∥BC、∠ABC=90°,
∴FD⊥AB,
∵EG⊥BC,
∴四边形BDEG是矩形,
∵AE平分∠BAC、CE平分∠ACB,
∴ED=EH=EG,∠DAE=∠HAE,
∴四边形BDEG是正方形,
在△DAE和△HAE中,
∵,
∴△DAE≌△HAE(AAS),
∴AD=AH,
同理△CGE≌△CHE,
∴CG=CH,
设BD=BG=x,则AD=AH=6﹣x、CG=CH=8﹣x,
∵AC===10,
∴6﹣x+8﹣x=10,
解得:x=2,
∴BD=DE=2,AD=4,
∵DF∥BC,
∴△ADF∽△ABC,
∴=,即=,
解得:DF=,
则EF=DF﹣DE=﹣2=,
故选:C.
7.解:∵△BPC是等边三角形,
∴BP=PC=BC,∠PBC=∠PCB=∠BPC=60°,
在正方形ABCD中,
∵AB=BC=CD,∠A=∠ADC=∠BCD=90°
∴∠ABE=∠DCF=30°,
∴BE=2AE;故①正确;
∵PC=CD,∠PCD=30°,
∴∠PDC=75°,
∴∠FDP=15°,
∵∠DBA=45°,
∴∠PBD=15°,
∴∠FDP=∠PBD,
∵∠DFP=∠BPC=60°,
∴△DFP∽△BPH;故②正确;
∵∠FDP=∠PBD=15°,∠ADB=45°,
∴∠PDB=30°,而∠DFP=60°,
∴∠PFD≠∠PDB,
∴△PFD与△PDB不会相似;故③错误;
∵∠PDH=∠PCD=30°,∠DPH=∠DPC,
∴△DPH∽△CPD,
∴,
∴DP2=PH PC,故④正确;
故选:C.
8.解:∵在 ABCD中,AO=AC,
∵点E是OA的中点,
∴AE=CE,
∵AD∥BC,
∴△AFE∽△CBE,
∴==,
∵AD=BC,
∴AF=AD,
∴=;故①正确;
∵S△AEF=4,=()2=,
∴S△BCE=36;故②正确;
∵==,
∴=,
∴S△ABE=12,故③正确;
∵BF不平行于CD,
∴△AEF与△ADC只有一个角相等,
∴△AEF与△ACD不一定相似,故④错误,
故选:D.
9.解:设正方形EFGH的边长EF=EH=x,
∵四边形EFGH是正方形,
∴∠HEF=∠EHG=90°,EF∥BC,
∴△AEF∽△ABC,
∵AD是△ABC的高,
∴∠HDN=90°,
∴四边形EHDN是矩形,
∴DN=EH=x,
∵△AEF∽△ABC,
∴=(相似三角形对应边上的高的比等于相似比),
∵BC=120,AD=60,
∴AN=60﹣x,
∴=,
解得:x=40,
∴AN=60﹣x=60﹣40=20.
故选:B.
10.解:在矩形ABCD中,AB=1,BC=,AD∥BC,
∴AC=2,
∵AC=4AF,
∴AF=,CF=,
∵AD∥BC,
∴==,
∴AE=,
∴BE=,
∴EF=BE=.
故选:A.
11.解:∵∠C=90°,AB=5,BC=4,
∴AC==3,
∵PQ∥AB,
∴∠ABD=∠BDQ,又∠ABD=∠QBD,
∴∠QBD=∠BDQ,
∴QB=QD,
∴QP=2QB,
∵PQ∥AB,
∴△CPQ∽△CAB,
∴==,即==,
解得,CP=,
∴AP=CA﹣CP=,
故选:B.
12.解:①∵四边形ABCD是正方形,
∴OC=OD,AC⊥BD,∠ODF=∠OCE=45°,
∵∠MON=90°,
∴∠COM=∠DOF,
∴△COE≌△DOF(ASA),
故①正确;
②∵△COE≌△DOF,
∴OE=OF,
∵∠MON=90°,
∴∠OEG=45°=∠FCG,
∵∠OGE=∠FGC,
∴△OGE∽△FGC,
故②正确;
③∵△COE≌△DOF,
∴S△COE=S△DOF,
∴,
故③正确;
④∵△COE≌△DOF,
∴OE=OF,
又∵∠EOF=90°,
∴△EOF是等腰直角三角形,
∴∠OEG=45°=∠OCE,
∵∠EOG=∠COE,
∴△OEG∽△OCE,
∴OE:OC=OG:OE,
∴OG OC=OE2,
∵OC=AC,OE=EF,
∴OG AC=EF2,
∵CE=DF,BC=CD,
∴BE=CF,
又∵Rt△CEF中,CF2+CE2=EF2,
∴BE2+DF2=EF2,
∴OG AC=BE2+DF2,
故④错误,
故选:B.
13.解:如图,作FN∥AD,交AB于N,交BE于M.
∵四边形ABCD是正方形,
∴AB∥CD,∵FN∥AD,
∴四边形ANFD是平行四边形,
∵∠D=90°,
∴四边形ANFD是矩形,
∵AE=3DE,设DE=a,则AE=3a,AD=AB=CD=FN=4a,AN=DF=2a,
∵AN=BN,MN∥AE,
∴BM=ME,
∴MN=a,
∴FM=a,
∵AE∥FM,
∴===,
故选:C.
14.解:如图,过A1作A1D⊥BO于点D.
设AD=DB1=x
则由△BA1D∽△BCO得:
=
解得x=
所以A2B1B2的边长为.
同理解得边长依次为,…
所以第n个等边三角形的边长等于.
故选:A.
二.填空题(共5小题,满分20分)
15.解:∵四边形EFGH是矩形,
∴EH∥BC,
∴△AEH∽△ABC,
∵AM⊥EH,AD⊥BC,
∴=,
设EH=3x,则有EF=2x,AM=AD﹣EF=2﹣2x,
∴=,
解得:x=,
则EH=.
故答案为:.
16.解:作AE⊥BH于E,BF⊥AH于F,如图,
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∵∠BHD=∠ABH+∠BAH=60°,∠BAH+∠CAH=60°,
∴∠ABH=∠CAH,
在△ABE和△CAH中
,
∴△ABE≌△CAH,
∴BE=AH,AE=CH,
在Rt△AHE中,∠AHE=∠BHD=60°,
∴sin∠AHE=,HE=AH,
∴AE=AH sin60°=AH,
∴CH=AH,
在Rt△AHC中,AH2+(AH)2=AC2=()2,解得AH=2,
∴BE=2,HE=1,AE=CH=,
∴BH=BE﹣HE=2﹣1=1,
在Rt△BFH中,HF=BH=,BF=,
∵BF∥CH,
∴△CHD∽△BFD,
∴===2,
∴DH=HF=×=.
故答案为.
17.解:如图,过点C作CM⊥DE于点M,过点E作EN⊥AC于点N,
∵BD=1,AD=5,
∴AB=BD+AD=6,
∵在Rt△ABC中,∠BAC=30°,∠B=90°﹣∠BAC=60°,
∴BC=AB=3,AC=BC=3,
在Rt△BCA与Rt△DCE中,
∵∠BAC=∠DEC=30°,
∴tan∠BAC=tan∠DEC,
∴,
∵∠BCA=∠DCE=90°,
∴∠BCA﹣∠DCA=∠DCE﹣∠DCA,
∴∠BCD=∠ACE,
∴△BCD∽△ACE,
∴∠CAE=∠B=60°,,
∴∠DAE=∠DAC+∠CAE=30°+60°=90°,,
∴AE=,
在Rt△ADE中,
DE===2,
在Rt△DCE中,∠DEC=30°,
∴∠EDC=60°,DC=DE=,
在Rt△DCM中,
MC=DC=,
在Rt△AEN中,
NE=AE=,
∵∠MFC=∠NFE,∠FMC=∠FNE=90°,
∴△MFC∽△NFE,
∴===,
方法二:求出AE后,证明△DFC∽△AFE,利用相似三角形的性质求解即可.
故答案为:.
18.解:∵在Rt△ABC中,∠BAC=90°,AB=15,AC=20,
∴BC==25,△ABC的面积=AB AC=×15×20=150,
∵AD=5,
∴CD=AC﹣AD=15,
∵DE⊥BC,
∴∠DEC=∠BAC=90°,
又∵∠C=∠C,
∴△CDE∽△CBA,
∴,即,
解得:CE=12,
∴BE=BC﹣CE=13,
∵△ABE的面积:△ABC的面积=BE:BC=13:25,
∴△ABE的面积=×150=78;
故答案为:78.
19.解:①∵四边形ABCD为正方形,
∴AB=BC=CD,
∵BE=EF=FC,CG=2GD,
∴BF=CG,
∵在△ABF和△BCG中,,
∴△ABF≌△BCG,
∴∠BAF=∠CBG,
∵∠BAF+∠BFA=90°,
∴∠CBG+∠BFA=90°,即AF⊥BG;①正确;
②∵在△BNF和△BCG中,,
∴△BNF∽△BCG,∴==,
∴BN=NF;②错误;
③作EH⊥AF,令AB=3,则BF=2,BE=EF=CF=1,
AF==,
∵S△ABF=AF BN=AB BF,
∴BN=,NF=BN=,
∴AN=AF﹣NF=,
∵E是BF中点,
∴EH是△BFN的中位线,
∴EH=,NH=,BN∥EH,
∴AH=,=,解得:MN=,
∴BM=BN﹣MN=,MG=BG﹣BM=,
∴=;③正确;
④连接AG,FG,根据③中结论,
则NG=BG﹣BN=,
∵S四边形CGNF=S△CFG+S△GNF=CG CF+NF NG=1+=,
S四边形ANGD=S△ANG+S△ADG=AN GN+AD DG=+=,
∴S四边形CGNF≠S四边形ANGD,④错误;
故答案为 ①③.
三.解答题(共5小题,满分58分)
20.解:(1)证明:∵CD=CP=4,DP=5,AC=3.5,BD=1,
∴AP=AC+CP=3.5+4=7.5,BP=BD+DP=1+5=6,
∴=,==,
∴,
∵∠DPC=∠APB,
∴△ABP∽△DCP;
(2)∵△ABP∽△DCP,
∴,
即:=,
∴AB=6.
21.解:(1)证明:如图,
∵AE⊥DE,
∴∠AED=90°,
∴∠AEB+∠DEC=90°,
∵AB⊥BC,DC⊥BC,
∴∠B+∠C=90°,
∴∠BAE=∠CED,
∴△ABE∽△ECD;
(2)在Rt△ABE中,由勾股定理得BE=3,
∴EC=BC﹣BE=2,
由(1)得△ABE∽△ECD,
∴,即,
解得CD=.
22.证明:在△ABC中,AB=4,BC=8,BD=2.
∴,,
∴,
又∵∠ABD=∠CBA,
∴△ABD∽△CBA,
∴∠BDA=∠BAC.
23.证明:(1)∵AG⊥BC,AF⊥DE于,
∴∠AFE=∠AGC=90°.
∵∠EAF=∠GAC
∴△AEF∽△ACG.
(2)由(1)知△AEF∽△ACG,
∴∠AEF=∠C
∵∠DAE=∠BAC(公共角),
∴△EAD∽△CAB.
∴∠ADE=∠B.
解:(3)由(2)知:△ADE∽△ABC,
∴.
由(1)知△AEF∽△ACG,
∴.
∴.
∵AD=3,AB=5,
∴.
24.解:(1)若0<t≤5,则AP=4t,AQ=2t.
则==,
又∵AO=10,AB=20,
∴==.
∴=.
又∵∠CAB=30°,
∴△APQ∽△ABO.
∴∠AQP=90°,即PQ⊥AC.
当5<t<10时,同理,可由△PCQ∽△BCO得∠PQC=90°,即PQ⊥AC.
∴在点P、Q运动过程中,始终有PQ⊥AC.
(2)①如图,在Rt△APM中,
∵∠PAM=30°,AP=4t,
∴AM=.
在△APQ中,∠AQP=90°,
∴AQ=2t,
∴QM=AC﹣2AQ=20﹣4t.
由AQ+QM=AM得:2t+20﹣4t=,
解得t=.
∴当t=时,点P、M、N在一直线上.
②存在这样的t,使△PMN是以PN为一直角边的直角三角形.
设l交AC于H.
如图1,当点N在AD上时,若PN⊥MN,则∠NMH=30°.
∴MH=2NH.得20﹣4t﹣=2×,解得t=2.
如图2,当点N在CD上时,若PM⊥PN,则∠HMP=30°.
∴MH=2PH,同理可得t=.
故当t=2或时,存在以PN为一直角边的直角三角形.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
