冀教版九年级数学下册32.3直棱柱和圆锥的侧面展开图课件(31张)
文档属性
| 名称 | 冀教版九年级数学下册32.3直棱柱和圆锥的侧面展开图课件(31张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-14 12:16:19 | ||
图片预览








文档简介
(共31张PPT)
32.3 直棱柱和圆锥的侧面展开图
第三十二章 投影与视图
课时导入
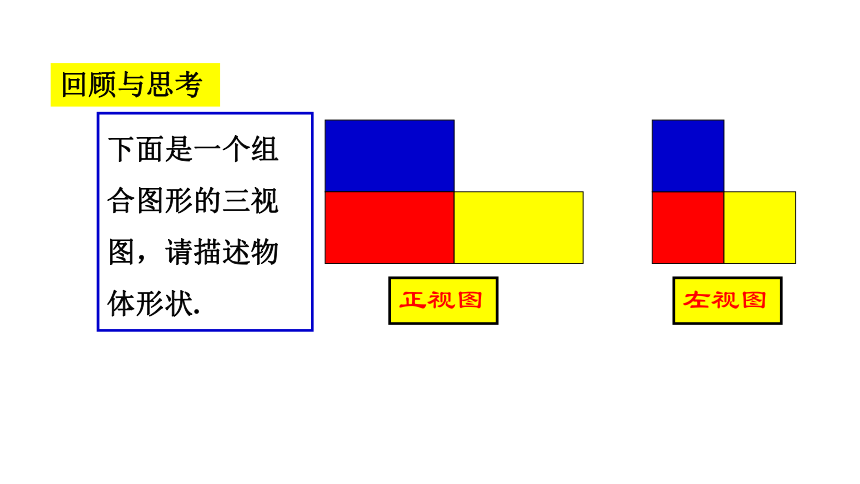
回顾与思考
下面是一个组合图形的三视图,请描述物体形状.
正视图
左视图
课时导入
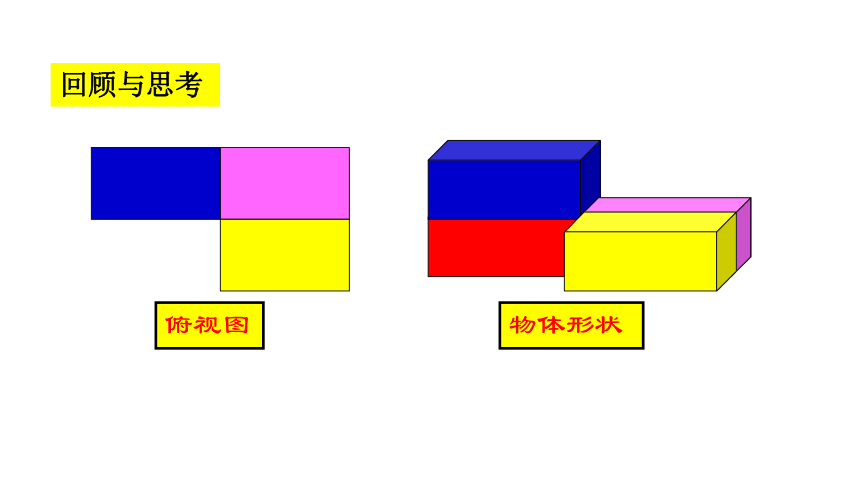
回顾与思考
俯视图
物体形状
知识点
直棱柱及其侧面展开图
知1-讲
感悟新知
1
如图所示,底面为正六边形的六棱柱,沿它的一条侧棱展开,就得到了这个六棱柱的侧面展开图.
知1-讲
感悟新知
特点:棱柱的表面展开图由两个_______的多边形和
一些__________组成.
相同
长方形
知1-讲
感悟新知
表面展开图:
有些几何体的表面,可以展开成平面图形,这个平面图形称为相应几何体的表面展开图.
提示:
沿直棱柱表面不同的棱剪开,可得到不同组合方式的表面展开图,即同一直棱柱的表面展开图可能有多种,它们都可以折叠成同一直棱柱.
知1-练
感悟新知
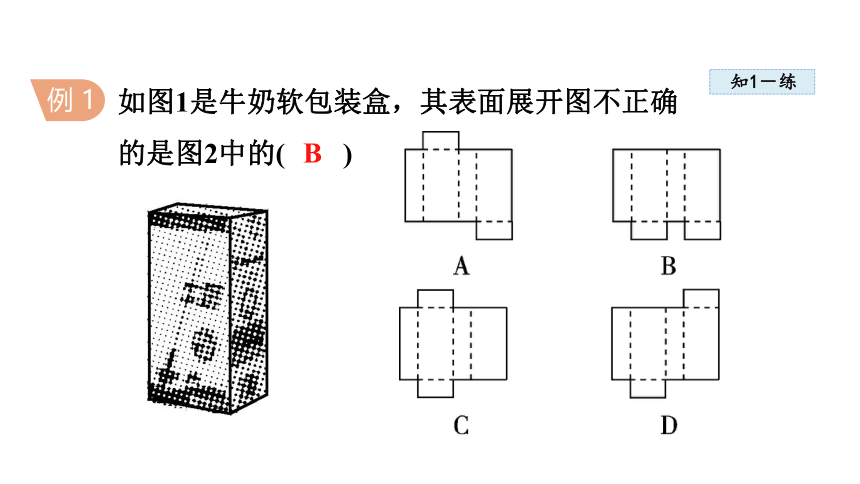
例 1
如图1是牛奶软包装盒,其表面展开图不正确
的是图2中的( )
B
知1-练
感悟新知
根据包装盒的形状可以发现,选项B中的对应位置有误;另外本题也可以把选项中的表面展开图进行折叠,看是否符合题意,通过折叠可以发现B是不正确的.
导引:
知1-讲
总 结
感悟新知
本题利用了转化思想,由几何体通过空间想象得到其表面展开图,所得的表面展开图要符合实际情况.
知1-练
感悟新知
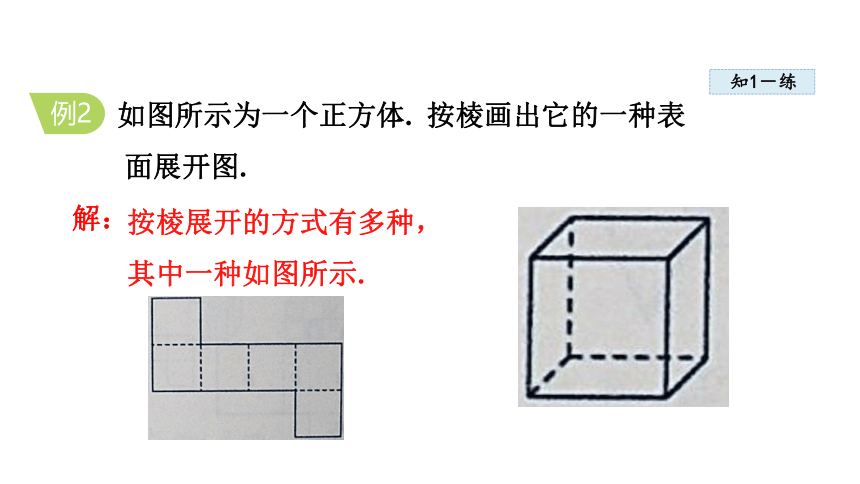
例2
如图所示为一个正方体. 按棱画出它的一种表
面展开图.
按棱展开的方式有多种,其中一种如图所示.
解:
知1-练
感悟新知
例 3
如图所示的四个图形都是由立体图形展开得到
的,相应的立体图形依次是( )
A.正方体、圆柱、三棱柱、圆锥
B.正方体、圆锥、三棱柱、圆柱
C.正方体、圆柱、三棱锥、圆锥
D.正方体、圆柱、四棱柱、圆锥
A
知1-练
感悟新知
观察图形,由立体图形及其表面展开图的特点可知相应的立体图形依次是正方体、圆柱、三棱柱、圆锥.故选A.
导引:
知1-练
感悟新知
1.
把如图所示的三棱柱展开,所得到的展开图是( )
B
知1-练
感悟新知
2.
如图,圆柱体的表面展开后得到的平面图形是( )
B
知1-练
感悟新知
3.
下列图形经过折叠不能围成棱柱的是( )
D
知1-练
感悟新知
4.
将如图所示的表面带有图案的正方体沿某些棱展开后,得到的图形是( )
C
知1-练
感悟新知
5.
如图是一个几何体的三视图,则这个几何体的侧面积是( )
A.12π cm2
B.8π cm2
C.6π cm2
D.3π cm2
C
知识点
圆锥及其侧面展开图
知2-讲
感悟新知
2
圆锥的表面展开图
将圆锥的侧面沿它的一条母线剪开,会得到圆锥的侧面展开图为扇形,其半径等于母线长,弧长是底面圆的周长.
知2-讲
感悟新知
特别提醒:
1. 圆锥的轴通过底面的圆心,并且垂直于底面;
2. 圆锥的母线长都相等;
3. 圆锥的母线l、高h 及底面圆的半径r 构成直角三角形,有l2=h2+r2,已知l,h 和r 中任意两个量都可以求出第三个量.
知2-讲
感悟新知
例4
如图,一个圆锥的高为3 cm,侧面展开图是半
圆.求:
(1)圆锥的母线长与底面半径之比;
(2)∠BAC的度数;
(3)圆锥的侧面积(结果保留π).
知2-练
感悟新知
(1)题直接根据圆锥的侧面展开图(扇形)的弧长等于
圆锥底面周长可得比值;
(3)题根据圆锥的侧面积是侧面展开图(扇形)的面积,
直接利用公式解题即可.
(1)设此圆锥的高为h,底面半径为r,
母线长AC=l,易知2πr=πl,
∴l∶r=2∶1.
导引:
解:
知2-练
感悟新知
(2)连接AO,则AO⊥OC,由(1)知 =2,
∴圆锥高与母线的夹角为30°,∴∠BAC=60°.
(3)由图可知l2=h2+r2,又∵h=3 cm,
∴(2r)2=(3 )2+r2,即4r2=27+r2,
解得r=3 cm,∴l=2r=6 cm,
∴圆锥的侧面积为 =18π(cm2).
知2-讲
总 结
感悟新知
本题运用了方程思想和数形结合思想,从而使问题得以转化,注意圆锥底面半径的确定.
随机事件
知2-练
感悟新知
1. 有一圆锥,它的高为8 cm,底面半径为6 cm,则
这个圆锥的侧面积是________ cm2. (结果保留π)
2. 如图所示,沿一条母线将圆锥侧面剪开并展平,得
到一个扇形.若圆锥的底面圆的半径r=2 cm,扇
形的圆心角θ=120°,则该圆锥
的母线长l为________cm.
60π
6
知2-练
感悟新知
如图,圆锥的侧面展开图是半径为3,圆心角为90°的扇形,则该圆锥的底面周长为( )
A.
B.
C.
D.
B
3.
随机事件
知2-练
感悟新知
4.
将一边长为2的正方形纸片折成四部分,再沿折痕折起来,恰好能不重叠地搭建成一个三棱锥,则三棱锥四个面中最小的面的面积是( )
A.1 B.
C. D.
C
随机事件
知2-练
感悟新知
5.
一个几何体的三视图如图所示,其中主视图和左视图都是腰长为4,底边长为2的等腰三角形,则这个几何体侧面展开图的面积为( )
A.2π
B. π
C.4π
D.8π
C
课堂小结
直棱柱和圆锥的侧面展开图
常见图形的侧面展开图:
圆锥的侧面展开图是一个扇形;
圆柱的侧面展开图是矩形;
正方体的表面展开图有11种情况;
棱柱的侧面展开图是矩形.
课堂小结
直棱柱和圆锥的侧面展开图
如图所示的是一多面体的表面展开图,每个面上都标注了字母,请回答:如果F面在前面,从左面看是B面,那么哪一面会在上面?
课堂小结
直棱柱和圆锥的侧面展开图
错解:C面会在上面.
诊断:将表面展开图折成立体图形时,分向里折和向外
折两种情况,错解中忽略了一种情况,因此造成
漏解.
正解:E面或C面会在上面.
课堂小结
直棱柱和圆锥的侧面展开图
易错点:将表面展开图折成立体图形时出错.
32.3 直棱柱和圆锥的侧面展开图
第三十二章 投影与视图
课时导入
回顾与思考
下面是一个组合图形的三视图,请描述物体形状.
正视图
左视图
课时导入
回顾与思考
俯视图
物体形状
知识点
直棱柱及其侧面展开图
知1-讲
感悟新知
1
如图所示,底面为正六边形的六棱柱,沿它的一条侧棱展开,就得到了这个六棱柱的侧面展开图.
知1-讲
感悟新知
特点:棱柱的表面展开图由两个_______的多边形和
一些__________组成.
相同
长方形
知1-讲
感悟新知
表面展开图:
有些几何体的表面,可以展开成平面图形,这个平面图形称为相应几何体的表面展开图.
提示:
沿直棱柱表面不同的棱剪开,可得到不同组合方式的表面展开图,即同一直棱柱的表面展开图可能有多种,它们都可以折叠成同一直棱柱.
知1-练
感悟新知
例 1
如图1是牛奶软包装盒,其表面展开图不正确
的是图2中的( )
B
知1-练
感悟新知
根据包装盒的形状可以发现,选项B中的对应位置有误;另外本题也可以把选项中的表面展开图进行折叠,看是否符合题意,通过折叠可以发现B是不正确的.
导引:
知1-讲
总 结
感悟新知
本题利用了转化思想,由几何体通过空间想象得到其表面展开图,所得的表面展开图要符合实际情况.
知1-练
感悟新知
例2
如图所示为一个正方体. 按棱画出它的一种表
面展开图.
按棱展开的方式有多种,其中一种如图所示.
解:
知1-练
感悟新知
例 3
如图所示的四个图形都是由立体图形展开得到
的,相应的立体图形依次是( )
A.正方体、圆柱、三棱柱、圆锥
B.正方体、圆锥、三棱柱、圆柱
C.正方体、圆柱、三棱锥、圆锥
D.正方体、圆柱、四棱柱、圆锥
A
知1-练
感悟新知
观察图形,由立体图形及其表面展开图的特点可知相应的立体图形依次是正方体、圆柱、三棱柱、圆锥.故选A.
导引:
知1-练
感悟新知
1.
把如图所示的三棱柱展开,所得到的展开图是( )
B
知1-练
感悟新知
2.
如图,圆柱体的表面展开后得到的平面图形是( )
B
知1-练
感悟新知
3.
下列图形经过折叠不能围成棱柱的是( )
D
知1-练
感悟新知
4.
将如图所示的表面带有图案的正方体沿某些棱展开后,得到的图形是( )
C
知1-练
感悟新知
5.
如图是一个几何体的三视图,则这个几何体的侧面积是( )
A.12π cm2
B.8π cm2
C.6π cm2
D.3π cm2
C
知识点
圆锥及其侧面展开图
知2-讲
感悟新知
2
圆锥的表面展开图
将圆锥的侧面沿它的一条母线剪开,会得到圆锥的侧面展开图为扇形,其半径等于母线长,弧长是底面圆的周长.
知2-讲
感悟新知
特别提醒:
1. 圆锥的轴通过底面的圆心,并且垂直于底面;
2. 圆锥的母线长都相等;
3. 圆锥的母线l、高h 及底面圆的半径r 构成直角三角形,有l2=h2+r2,已知l,h 和r 中任意两个量都可以求出第三个量.
知2-讲
感悟新知
例4
如图,一个圆锥的高为3 cm,侧面展开图是半
圆.求:
(1)圆锥的母线长与底面半径之比;
(2)∠BAC的度数;
(3)圆锥的侧面积(结果保留π).
知2-练
感悟新知
(1)题直接根据圆锥的侧面展开图(扇形)的弧长等于
圆锥底面周长可得比值;
(3)题根据圆锥的侧面积是侧面展开图(扇形)的面积,
直接利用公式解题即可.
(1)设此圆锥的高为h,底面半径为r,
母线长AC=l,易知2πr=πl,
∴l∶r=2∶1.
导引:
解:
知2-练
感悟新知
(2)连接AO,则AO⊥OC,由(1)知 =2,
∴圆锥高与母线的夹角为30°,∴∠BAC=60°.
(3)由图可知l2=h2+r2,又∵h=3 cm,
∴(2r)2=(3 )2+r2,即4r2=27+r2,
解得r=3 cm,∴l=2r=6 cm,
∴圆锥的侧面积为 =18π(cm2).
知2-讲
总 结
感悟新知
本题运用了方程思想和数形结合思想,从而使问题得以转化,注意圆锥底面半径的确定.
随机事件
知2-练
感悟新知
1. 有一圆锥,它的高为8 cm,底面半径为6 cm,则
这个圆锥的侧面积是________ cm2. (结果保留π)
2. 如图所示,沿一条母线将圆锥侧面剪开并展平,得
到一个扇形.若圆锥的底面圆的半径r=2 cm,扇
形的圆心角θ=120°,则该圆锥
的母线长l为________cm.
60π
6
知2-练
感悟新知
如图,圆锥的侧面展开图是半径为3,圆心角为90°的扇形,则该圆锥的底面周长为( )
A.
B.
C.
D.
B
3.
随机事件
知2-练
感悟新知
4.
将一边长为2的正方形纸片折成四部分,再沿折痕折起来,恰好能不重叠地搭建成一个三棱锥,则三棱锥四个面中最小的面的面积是( )
A.1 B.
C. D.
C
随机事件
知2-练
感悟新知
5.
一个几何体的三视图如图所示,其中主视图和左视图都是腰长为4,底边长为2的等腰三角形,则这个几何体侧面展开图的面积为( )
A.2π
B. π
C.4π
D.8π
C
课堂小结
直棱柱和圆锥的侧面展开图
常见图形的侧面展开图:
圆锥的侧面展开图是一个扇形;
圆柱的侧面展开图是矩形;
正方体的表面展开图有11种情况;
棱柱的侧面展开图是矩形.
课堂小结
直棱柱和圆锥的侧面展开图
如图所示的是一多面体的表面展开图,每个面上都标注了字母,请回答:如果F面在前面,从左面看是B面,那么哪一面会在上面?
课堂小结
直棱柱和圆锥的侧面展开图
错解:C面会在上面.
诊断:将表面展开图折成立体图形时,分向里折和向外
折两种情况,错解中忽略了一种情况,因此造成
漏解.
正解:E面或C面会在上面.
课堂小结
直棱柱和圆锥的侧面展开图
易错点:将表面展开图折成立体图形时出错.
