冀教版九年级数学下册29.3.1 切线的性质课件(第一课时 16张张)
文档属性
| 名称 | 冀教版九年级数学下册29.3.1 切线的性质课件(第一课时 16张张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 940.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-14 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
29.3 切线的性质与判定
第二十九章 直线与圆的位置关系
课时导入
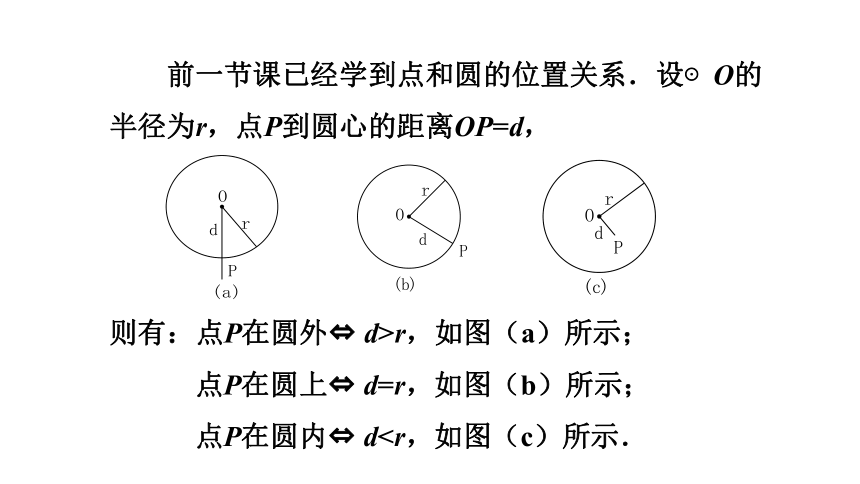
前一节课已经学到点和圆的位置关系.设⊙O的
半径为r,点P到圆心的距离OP=d,
则有:点P在圆外 d>r,如图(a)所示;
点P在圆上 d=r,如图(b)所示;
点P在圆内 d知识点
切线的性质定理
知1-讲
感悟新知
1
前面我们已学过的切线的性质有哪些?
答:①切线和圆有且只有一个公共点;
②切线和圆心的距离等于半径.
切线还有什么性质?
知1-讲
感悟新知
切线的性质定理:圆的切线垂直于过切点的半径.
感悟新知
知1-讲
特别解读
1. 性质定理的题设有两个条件:
(1)圆的切线;
(2)半径过切点.
应用时缺一不可.
2. 运用切线的性质最常见的辅助线:连接圆心和切点.
感悟新知
知1-练
例 1
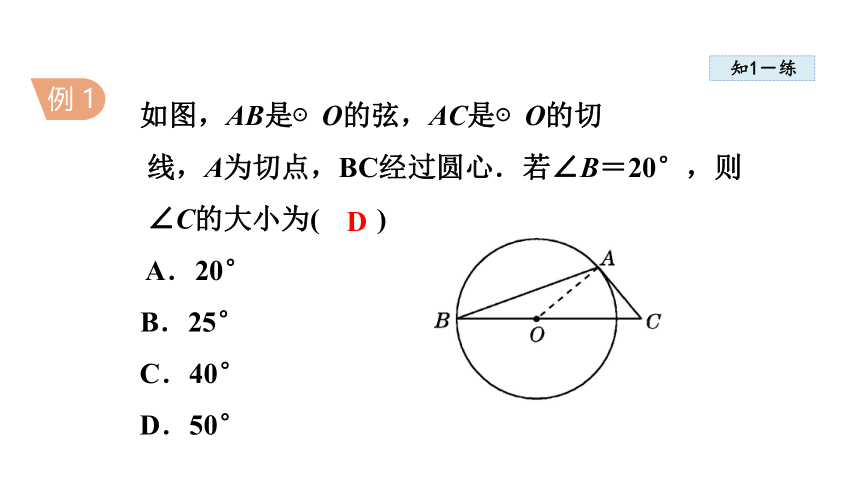
如图,AB是⊙O的弦,AC是⊙O的切
线,A为切点,BC经过圆心.若∠B=20°,则
∠C的大小为( )
A.20°
B.25°
C.40°
D.50°
D
感悟新知
知1-练
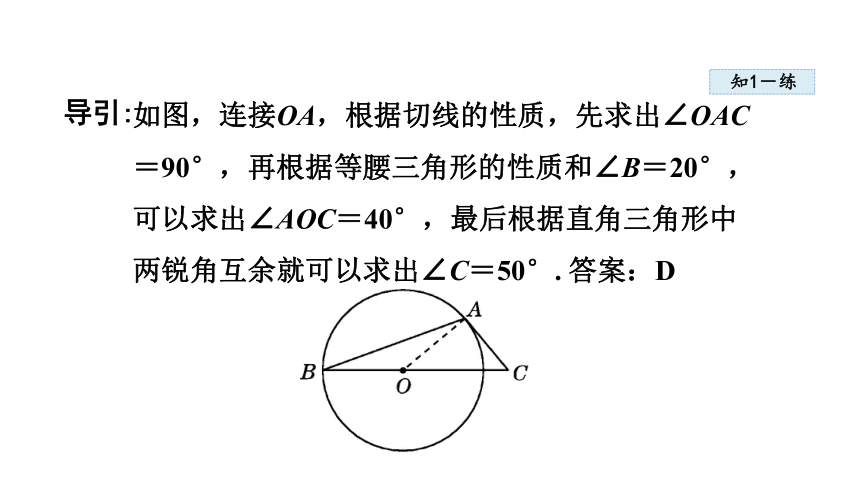
如图,连接OA,根据切线的性质,先求出∠OAC=90°,再根据等腰三角形的性质和∠B=20°,可以求出∠AOC=40°,最后根据直角三角形中两锐角互余就可以求出∠C=50°. 答案:D
导引:
知1-讲
总 结
感悟新知
(1)半径处处相等可得等腰三角形,从而底角相等;
(2)切线垂直于过切点的半径得直角三角形,从而
两锐角互余.
知1-讲
感悟新知
a(地平线)
如图,PA为⊙O的切线,切点为A,OP = 2,∠APO=30°求⊙O的半径.
1
连接OA,则OA为⊙O的半径,因为PA是⊙O的切线,所以OA⊥AP,又∠APO=30°,OP=2,所以OA=
OP=1,即⊙O的半径为1.
解:
知识点
切线性质定理的应用
知2-练
感悟新知
2
如图,△ABC内接于⊙O,AB是⊙O的直径,∠BAC=2∠B,⊙O的切线AP与OC的延长线相交于点P,若PA=6 cm,求AC的长.
例2
感悟新知
知2-练
根据AB是⊙O的直径求出∠ACB=90°,再根据∠BAC=2∠B求出∠B=30°,∠BAC=60°,得出△AOC是等边三角形,得出∠AOC=60°,OA=AC,在Rt△OAP中,求出OA,即可求出AC的长.
导引:
感悟新知
知2-练
∵AB是⊙O的直径,∴∠ACB=90°.
又∵∠BAC=2∠B,∴∠B=30°,∠BAC=60°.
又∵OA=OC,∴△AOC是等边三角形,
∴∠AOC=60°,AC=OA.
∵PA是⊙O的切线,∴∠OAP=90°.
在Rt△OAP中,∵PA=6 cm,∠AOP=60°,
∴OA= =6(cm),
∴AC=OA=6 cm.
解:
知2-讲
总 结
感悟新知
圆的切线垂直于过切点的半径,这个性质为解题提供了隐含条件.当已知直线为圆的切线时,可以连接过切点的半径,由切线的性质得出直角三角形,再根据锐角三角函数求解.
感悟新知
知2-讲
特别解读
切线必须同时具备两个条件:
1. 直线过半径的外端;
2. 直线垂直于这条半径.
感悟新知
知2-讲
如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan ∠OAB= ,则AB的长是( )
A.4
B.2
C.8
D.4
1
C
课堂小结
切线
圆的切线垂直于过切点的半径. 已知直线满足:
(1)过圆心;
(2)过切点;
(3)垂直于直线任意两个,就可得到第三个.
29.3 切线的性质与判定
第二十九章 直线与圆的位置关系
课时导入
前一节课已经学到点和圆的位置关系.设⊙O的
半径为r,点P到圆心的距离OP=d,
则有:点P在圆外 d>r,如图(a)所示;
点P在圆上 d=r,如图(b)所示;
点P在圆内 d
切线的性质定理
知1-讲
感悟新知
1
前面我们已学过的切线的性质有哪些?
答:①切线和圆有且只有一个公共点;
②切线和圆心的距离等于半径.
切线还有什么性质?
知1-讲
感悟新知
切线的性质定理:圆的切线垂直于过切点的半径.
感悟新知
知1-讲
特别解读
1. 性质定理的题设有两个条件:
(1)圆的切线;
(2)半径过切点.
应用时缺一不可.
2. 运用切线的性质最常见的辅助线:连接圆心和切点.
感悟新知
知1-练
例 1
如图,AB是⊙O的弦,AC是⊙O的切
线,A为切点,BC经过圆心.若∠B=20°,则
∠C的大小为( )
A.20°
B.25°
C.40°
D.50°
D
感悟新知
知1-练
如图,连接OA,根据切线的性质,先求出∠OAC=90°,再根据等腰三角形的性质和∠B=20°,可以求出∠AOC=40°,最后根据直角三角形中两锐角互余就可以求出∠C=50°. 答案:D
导引:
知1-讲
总 结
感悟新知
(1)半径处处相等可得等腰三角形,从而底角相等;
(2)切线垂直于过切点的半径得直角三角形,从而
两锐角互余.
知1-讲
感悟新知
a(地平线)
如图,PA为⊙O的切线,切点为A,OP = 2,∠APO=30°求⊙O的半径.
1
连接OA,则OA为⊙O的半径,因为PA是⊙O的切线,所以OA⊥AP,又∠APO=30°,OP=2,所以OA=
OP=1,即⊙O的半径为1.
解:
知识点
切线性质定理的应用
知2-练
感悟新知
2
如图,△ABC内接于⊙O,AB是⊙O的直径,∠BAC=2∠B,⊙O的切线AP与OC的延长线相交于点P,若PA=6 cm,求AC的长.
例2
感悟新知
知2-练
根据AB是⊙O的直径求出∠ACB=90°,再根据∠BAC=2∠B求出∠B=30°,∠BAC=60°,得出△AOC是等边三角形,得出∠AOC=60°,OA=AC,在Rt△OAP中,求出OA,即可求出AC的长.
导引:
感悟新知
知2-练
∵AB是⊙O的直径,∴∠ACB=90°.
又∵∠BAC=2∠B,∴∠B=30°,∠BAC=60°.
又∵OA=OC,∴△AOC是等边三角形,
∴∠AOC=60°,AC=OA.
∵PA是⊙O的切线,∴∠OAP=90°.
在Rt△OAP中,∵PA=6 cm,∠AOP=60°,
∴OA= =6(cm),
∴AC=OA=6 cm.
解:
知2-讲
总 结
感悟新知
圆的切线垂直于过切点的半径,这个性质为解题提供了隐含条件.当已知直线为圆的切线时,可以连接过切点的半径,由切线的性质得出直角三角形,再根据锐角三角函数求解.
感悟新知
知2-讲
特别解读
切线必须同时具备两个条件:
1. 直线过半径的外端;
2. 直线垂直于这条半径.
感悟新知
知2-讲
如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan ∠OAB= ,则AB的长是( )
A.4
B.2
C.8
D.4
1
C
课堂小结
切线
圆的切线垂直于过切点的半径. 已知直线满足:
(1)过圆心;
(2)过切点;
(3)垂直于直线任意两个,就可得到第三个.
