冀教版九年级数学下册29.2直线与圆的位置关系课件(21张)
文档属性
| 名称 | 冀教版九年级数学下册29.2直线与圆的位置关系课件(21张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-14 12:21:23 | ||
图片预览






文档简介
(共21张PPT)
第二十九章 直线与圆的位置关系
29.2 直线与圆的位置关系
第二十九章 直线与圆的位置关系
课时导入
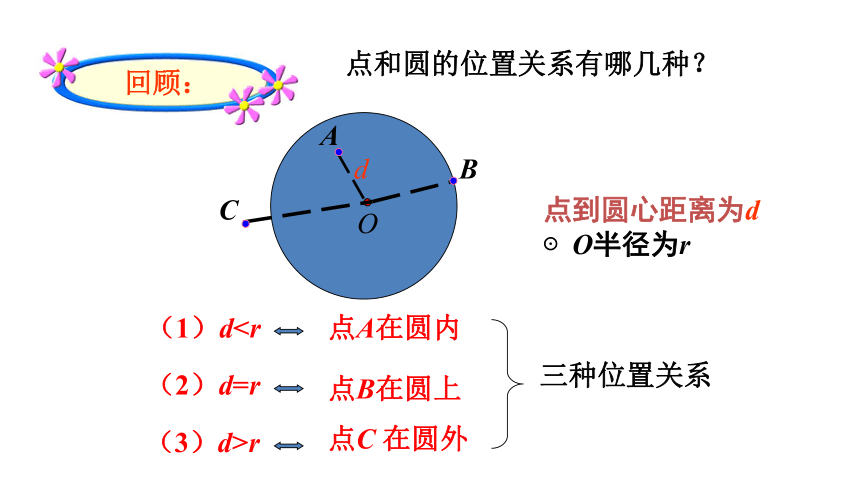
点和圆的位置关系有哪几种?
(1)d(2)d=r
(3)d>r
A
B
C
d
点A在圆内
点B在圆上
点C 在圆外
三种位置关系
O
点到圆心距离为d
⊙O半径为r
回顾:
知识点
直线与圆的位置关系与直线与圆的公共点个数间的关系
知1-讲
感悟新知
1
清晨,一轮红日从东方冉冉升起,太阳的轮廓就像一个运动的圆,从地平线下渐渐升到空中.在此过程中,太阳轮廓与地平线有几种不同的位置关系呢
知1-讲
感悟新知
●O
●O
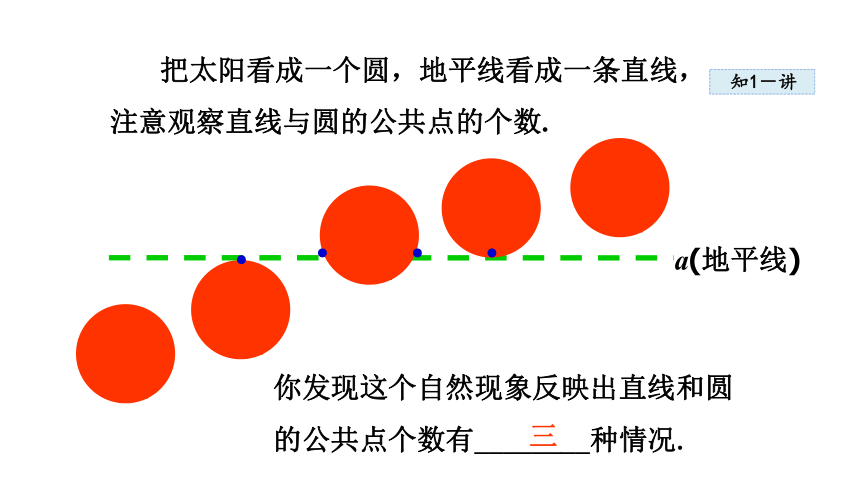
把太阳看成一个圆,地平线看成一条直线,
注意观察直线与圆的公共点的个数.
a(地平线)
a(地平线)
●O
●O
●O
三
你发现这个自然现象反映出直线和圆
的公共点个数有________种情况.
●
●
●
●
知1-讲
感悟新知
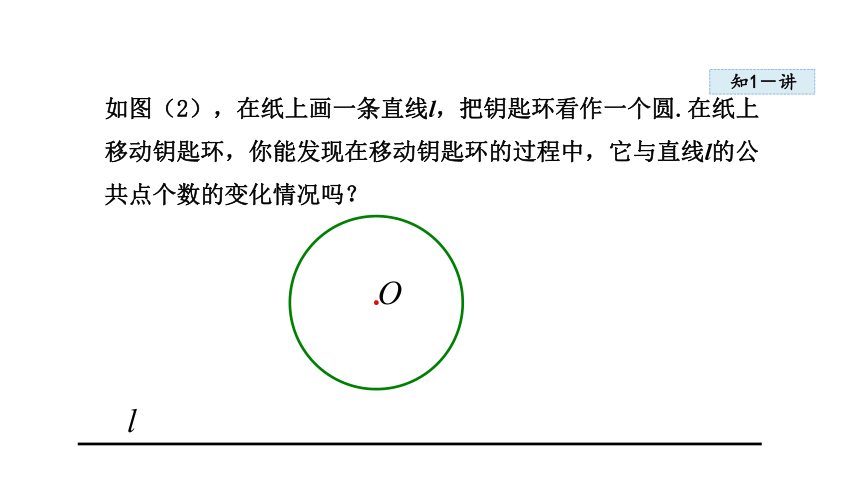
如图(2),在纸上画一条直线l,把钥匙环看作一个圆.在纸上
移动钥匙环,你能发现在移动钥匙环的过程中,它与直线l的公
共点个数的变化情况吗?
l
O
知1-讲
感悟新知
直线和圆只有一个公共点,这时我们就说这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点.
直线和圆有两个公共点,这时我们就说这条直线和圆相交,这条直线叫做圆的割线.
直线和圆没有公共点,这时我们就说这条直线和圆相离.
知1-讲
感悟新知
要点提醒
1. 如果一条直线满足下列三个条件中的任意两个,
那么第三个也满足:
(1)过圆心;
(2)过切点;
(3)垂直于切线.
2. 根据切线的定义,可以知道切线的性质有:
(1)切线和圆只有一个公共点;
(2)切点到圆心的距离等于半径.
感悟新知
知1-练
例 1
若直线l与⊙O有公共交点,则直线l与⊙O
的位置关系是( )
A.相交 B.相切
C.相离 D.相切或相交
直线l与⊙O有公共交点有两种情况:(1)有惟一公共交点,此时直线l与⊙O相切;(2)有两个交点,此时直线l与⊙O相交,故应选D.
D
导引:
感悟新知
知1-练
若直线m与⊙O的公共点个数不小于1,则直线m与⊙O的位置关系是( )
A.相交 B.相切
C.相交或相切 D.相离
1
C
知识点
直线与圆的位置关系的判定
知2-讲
感悟新知
2
思考:
设⊙O的半径为r,圆心O到直线l的距离为d,在直线和圆的不同位置关系中,你能根据d与r的大小关系确定直线和圆的位置关系吗?
感悟新知
知2-讲
如图,圆心O到直线的距离d与⊙O的半径r的大小有什么关系
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
感悟新知
知2-讲
1)直线和圆相交
d______r;
2) 直线和圆相切
3) 直线和圆相离
<
d______r;
=
d______r;
>
感悟新知
知2-练
例2
如图,在 Rt△ABC 中,∠C= 90°,AC= 3 cm,BC= 4 cm. 以点C为圆心,2cm,2.4cm,3cm分别为半径画⊙C,斜边AB分别与⊙C有怎样的位置关系?为什么?
感悟新知
知2-练
如图,过点C作CD丄AB,垂足为D. 在 Rt△ABC中,
由三角形的面积公式,并整理,得
AC BC=AB CD.
从而
即圆心C到斜边AB的距离d=2.4 cm.
当r=2cm时,d>r,斜边AB与⊙C相离.
当r=2.4cm时,d=r,斜边AB与⊙C相切.
当r=3cm时,d<r,斜边AB与⊙C相交.
解:
感悟新知
知2-练
已知一个圆的直径为10. 如果这个圆的圆心到一
条直线的距离分别等于3,5,6,那么这条直线与这个圆的位置关系分别是怎样的?
1
因为圆的直径为10,所以圆的半径为5.当直线与圆心的距离等于3时,因为3<5,所以直线与圆相交;
当直线与圆心的距离等于5时,因为5=5,所以直线与圆相切;
当直线与圆心的距离等于6时,因为6>5,所以直线与圆相离.
解:
知识点
直线与圆的位置关系的性质
知3-练
感悟新知
3
在Rt△ABC中,AC=3 cm,BC=4 cm,∠ACB=
90°.若以点C为圆心,r为半径的圆与直线AB不相
离,求r的取值范围.
⊙C与直线AB不相离,即⊙C与直线AB相交或相
切,因此只需点C到直线AB的距离小于或等于r.
导引:
例 3
感悟新知
知3-练
如图,过点C作CD⊥AB于点D.
在Rt△ABC中,
AC=3 cm,BC=4 cm,∠ACB=90°,
∴AB=
又∵S△ABC= AB CD= AC BC,
∴CD=2.4 cm.
∴r≥2.4 cm.
解:
知3-讲
总 结
感悟新知
(1)直线和圆的位置关系的应用过程实质是一种数形
结合思想的转化过程,它始终是“数”:圆心到
直线的距离与圆的半径大小,与“形”:直线和
圆的位置关系之间的相互转化.
(2)圆心到直线的距离通常用勾股定理与面积相等法
求出.
感悟新知
知3-练
如图,给定一个半径长为2的圆,圆心O到水平直
线l的距离为d,即OM=d.我们把圆上到直线l的距离等于1的点的个数记为m.如d=0时,l为经过圆心O的一条直线,此时圆上有四个到直线l的距离等于1的点,即m=4,由此可知:
(1)当d=3时,m=________;
(2)当m=2时,d的取值范围
是___________.
1
1
1<d<3
课堂小结
直线与圆的位置关系
1.直线和圆的位置关系:相交、相切、相离.
(1)从公共点数来判断;
(2)从d与r间的数量关系来判断.
课堂小结
2.直线和圆的位置关系的性质与判定:
(1)直线和圆相离 d>r;
(2)直线和圆相切 d=r;
(3)直线和圆相交 d<r.
直线与圆的位置关系
第二十九章 直线与圆的位置关系
29.2 直线与圆的位置关系
第二十九章 直线与圆的位置关系
课时导入
点和圆的位置关系有哪几种?
(1)d
(3)d>r
A
B
C
d
点A在圆内
点B在圆上
点C 在圆外
三种位置关系
O
点到圆心距离为d
⊙O半径为r
回顾:
知识点
直线与圆的位置关系与直线与圆的公共点个数间的关系
知1-讲
感悟新知
1
清晨,一轮红日从东方冉冉升起,太阳的轮廓就像一个运动的圆,从地平线下渐渐升到空中.在此过程中,太阳轮廓与地平线有几种不同的位置关系呢
知1-讲
感悟新知
●O
●O
把太阳看成一个圆,地平线看成一条直线,
注意观察直线与圆的公共点的个数.
a(地平线)
a(地平线)
●O
●O
●O
三
你发现这个自然现象反映出直线和圆
的公共点个数有________种情况.
●
●
●
●
知1-讲
感悟新知
如图(2),在纸上画一条直线l,把钥匙环看作一个圆.在纸上
移动钥匙环,你能发现在移动钥匙环的过程中,它与直线l的公
共点个数的变化情况吗?
l
O
知1-讲
感悟新知
直线和圆只有一个公共点,这时我们就说这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点.
直线和圆有两个公共点,这时我们就说这条直线和圆相交,这条直线叫做圆的割线.
直线和圆没有公共点,这时我们就说这条直线和圆相离.
知1-讲
感悟新知
要点提醒
1. 如果一条直线满足下列三个条件中的任意两个,
那么第三个也满足:
(1)过圆心;
(2)过切点;
(3)垂直于切线.
2. 根据切线的定义,可以知道切线的性质有:
(1)切线和圆只有一个公共点;
(2)切点到圆心的距离等于半径.
感悟新知
知1-练
例 1
若直线l与⊙O有公共交点,则直线l与⊙O
的位置关系是( )
A.相交 B.相切
C.相离 D.相切或相交
直线l与⊙O有公共交点有两种情况:(1)有惟一公共交点,此时直线l与⊙O相切;(2)有两个交点,此时直线l与⊙O相交,故应选D.
D
导引:
感悟新知
知1-练
若直线m与⊙O的公共点个数不小于1,则直线m与⊙O的位置关系是( )
A.相交 B.相切
C.相交或相切 D.相离
1
C
知识点
直线与圆的位置关系的判定
知2-讲
感悟新知
2
思考:
设⊙O的半径为r,圆心O到直线l的距离为d,在直线和圆的不同位置关系中,你能根据d与r的大小关系确定直线和圆的位置关系吗?
感悟新知
知2-讲
如图,圆心O到直线的距离d与⊙O的半径r的大小有什么关系
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
感悟新知
知2-讲
1)直线和圆相交
d______r;
2) 直线和圆相切
3) 直线和圆相离
<
d______r;
=
d______r;
>
感悟新知
知2-练
例2
如图,在 Rt△ABC 中,∠C= 90°,AC= 3 cm,BC= 4 cm. 以点C为圆心,2cm,2.4cm,3cm分别为半径画⊙C,斜边AB分别与⊙C有怎样的位置关系?为什么?
感悟新知
知2-练
如图,过点C作CD丄AB,垂足为D. 在 Rt△ABC中,
由三角形的面积公式,并整理,得
AC BC=AB CD.
从而
即圆心C到斜边AB的距离d=2.4 cm.
当r=2cm时,d>r,斜边AB与⊙C相离.
当r=2.4cm时,d=r,斜边AB与⊙C相切.
当r=3cm时,d<r,斜边AB与⊙C相交.
解:
感悟新知
知2-练
已知一个圆的直径为10. 如果这个圆的圆心到一
条直线的距离分别等于3,5,6,那么这条直线与这个圆的位置关系分别是怎样的?
1
因为圆的直径为10,所以圆的半径为5.当直线与圆心的距离等于3时,因为3<5,所以直线与圆相交;
当直线与圆心的距离等于5时,因为5=5,所以直线与圆相切;
当直线与圆心的距离等于6时,因为6>5,所以直线与圆相离.
解:
知识点
直线与圆的位置关系的性质
知3-练
感悟新知
3
在Rt△ABC中,AC=3 cm,BC=4 cm,∠ACB=
90°.若以点C为圆心,r为半径的圆与直线AB不相
离,求r的取值范围.
⊙C与直线AB不相离,即⊙C与直线AB相交或相
切,因此只需点C到直线AB的距离小于或等于r.
导引:
例 3
感悟新知
知3-练
如图,过点C作CD⊥AB于点D.
在Rt△ABC中,
AC=3 cm,BC=4 cm,∠ACB=90°,
∴AB=
又∵S△ABC= AB CD= AC BC,
∴CD=2.4 cm.
∴r≥2.4 cm.
解:
知3-讲
总 结
感悟新知
(1)直线和圆的位置关系的应用过程实质是一种数形
结合思想的转化过程,它始终是“数”:圆心到
直线的距离与圆的半径大小,与“形”:直线和
圆的位置关系之间的相互转化.
(2)圆心到直线的距离通常用勾股定理与面积相等法
求出.
感悟新知
知3-练
如图,给定一个半径长为2的圆,圆心O到水平直
线l的距离为d,即OM=d.我们把圆上到直线l的距离等于1的点的个数记为m.如d=0时,l为经过圆心O的一条直线,此时圆上有四个到直线l的距离等于1的点,即m=4,由此可知:
(1)当d=3时,m=________;
(2)当m=2时,d的取值范围
是___________.
1
1
1<d<3
课堂小结
直线与圆的位置关系
1.直线和圆的位置关系:相交、相切、相离.
(1)从公共点数来判断;
(2)从d与r间的数量关系来判断.
课堂小结
2.直线和圆的位置关系的性质与判定:
(1)直线和圆相离 d>r;
(2)直线和圆相切 d=r;
(3)直线和圆相交 d<r.
直线与圆的位置关系
