第2章 一元二次方程单元复习小结(共25张PPT)
文档属性
| 名称 | 第2章 一元二次方程单元复习小结(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 724.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-13 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
单元复习
第二章
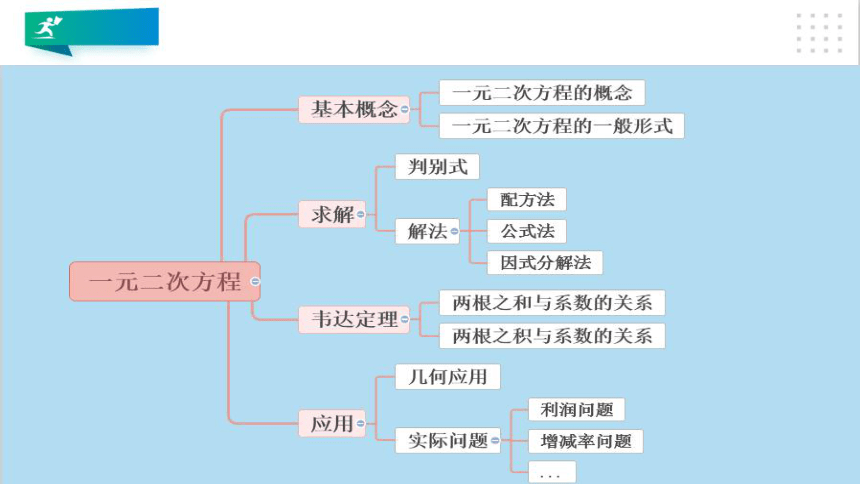
一元二次方程
2021-2022学年九年级数学上册同步(北师版)
本
章
知
识
架
构
知
识
专
题
要点梳理
ax2+bx+c=0(a、b、c为常数,a___0).其中ax2是二次项,a是二次项系数,bx是一次项,b是一次项系数,c是常数项.
1.概念:
只含有___未知数,并且未知数的最高次数为___的_____方程.
一、一元二方程的概念
2.一般形式:
1
≠
2
整式
解法 方程类型 注意事项
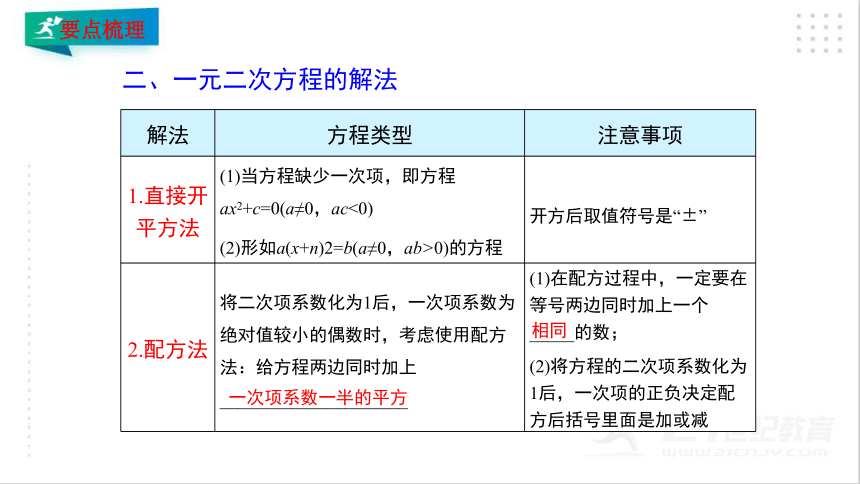
1.直接开平方法 (1)当方程缺少一次项,即方程ax2+c=0(a≠0,ac<0) (2)形如a(x+n)2=b(a≠0,ab>0)的方程 开方后取值符号是“±”
2.配方法 将二次项系数化为1后,一次项系数为绝对值较小的偶数时,考虑使用配方法:给方程两边同时加上_____________________ (1)在配方过程中,一定要在等号两边同时加上一个_____的数;
(2)将方程的二次项系数化为1后,一次项的正负决定配方后括号里面是加或减
二、一元二次方程的解法
一次项系数一半的平方
相同
要点梳理
解法 方程类型 注意事项
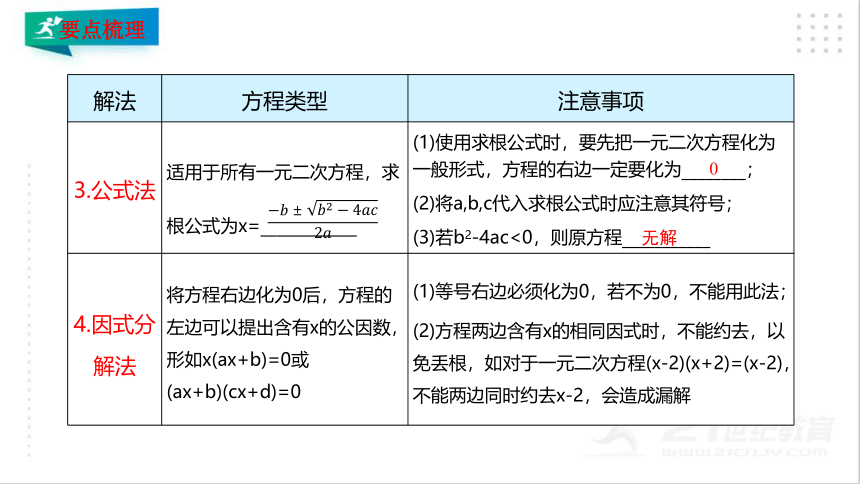
3.公式法 适用于所有一元二次方程,求根公式为x=____________ (1)使用求根公式时,要先把一元二次方程化为一般形式,方程的右边一定要化为________;
(2)将a,b,c代入求根公式时应注意其符号;
(3)若b2-4ac<0,则原方程___________
4.因式分解法 将方程右边化为0后,方程的左边可以提出含有x的公因数,形如x(ax+b)=0或(ax+b)(cx+d)=0 (1)等号右边必须化为0,若不为0,不能用此法;
(2)方程两边含有x的相同因式时,不能约去,以免丢根,如对于一元二次方程(x-2)(x+2)=(x-2),不能两边同时约去x-2,会造成漏解
0
无解
要点梳理
1.b2-4ac>0 一元二次方程有两个________的实数根
2._________ 一元二次方程有两个相等的实数根
3._________ 一元二次方程没有实数根
三、一元二次方程根的判别式
1.一元二次方程ax2+bx+c=0的根的判别式为:b2-4ac.
2.与根的关系
不相等
b2-4ac=0
b2-4ac<0
要点梳理
三、一元二次方程根的判别式
若所给方程的二次项系数含有字母,求字母的取值范围时,应记住一元二次方程二次项系数不为0这一条件.若未指明方程类型,需分情况(二次项系数为0和二次项系数不为0)讨论
3.注意事项
要点梳理
四、一元二次方程的实际应用
①.
②.若起始量为a,平均增长率为x,终止量为b,增长次数为2,则有___________
③.若起始量为a,平均增长率为x,终止量为b,下降次数为2,则有___________
1.平均变化率问题
a(1+x)2=b
a(1-x)2=b
要点梳理
四、一元二次方程的实际应用
①利润=售价-成本.
2.利润问题
②总利润=总售价-总成本.
③总利润=单个利润×总数量.
利润率=
④
要点梳理
四、一元二次方程的实际应用
3.几何问题
①解题时注意联系图形中有关的几何定理、面积和体积公式;
②不容易直接解决的问题可考虑添加辅助线;
③重视数形结合的思想方法
要点梳理
考点专练
考点一 用配方法解方程
例1:用配方法解方程: 3x2 +18x +24 = 0.
解析: 用配方法解一元二次方程,关键的一步是将二次项系数已化为1的方程的两边加上一次项系数一半的平方,转化为(x+m)2=n的形式,当n≥0时,直接开平方求得方程的根.
考点专练
解:方程两边同时除以3,得
x2 + 6x + 8 = 0 .
移项,得 x2 + 6x = -8 ,
配方, 得 (x + 3)2 = 1.
开平方, 得 x + 3 = ±1.
解得 x1 = -2 , x2= -4 .
例1:用配方法解方程: 3x2 +18x +24 = 0.
考点二 用公式法解方程
例2:用公式法解方程:x2-4x-1=0.
解析: 用公式法解方程时应先把一元二次方程化为一般形式,再确定a,b,c的值.
考点专练
根据公式法,我们可以利用b2-4ac的值判断一元二次方程根的情况:当b2-4ac>0时,方程有两个不相等的实数根;当b2-4ac=0时,方程有两个相等的实数根;当b2-4ac<0时,方程无实数根.反之,知道一元二次方程根的情况,也可以判断b2-4ac的符号.
方法技巧
考点三 用因式分解法解方程
例3:用因式分解法解方程:(x -3)2 + 3-x =0.
解析: (1)经过变形后可用提取公因式法分解因式,(2)可直接将方程左边分解因式.
解:(1)原方程变形为 (x-3)2-(x-3)=0,
(x-3)(x-3-1)=0,
即 (x-3)(x-4)=0,
x-3=0 或x-4=0,
∴x1=3,x2=4.
考点专练
考点专练
当一元二次方程的一边为0,而另一边易于分解成两个一次因式的乘积时,我们可以利用因式分解法解一元二次方程.用式子表示:若a·b=0,则a=0或b=0,反之也成立.有时遇到解高次方程时,也可以利用这种方式降次.如x4-16=0,则(x2+4)(x+2)(x-2)=0,其左边是三个因式,其中有一个二次的因式,其余两个是一次的因式.分解因式法把一个一元二次方程化为两个一元一次方程来解,体现了一种“降次”的思想.
方法技巧
考点五 一元二次方程根与系数的关系
例4 已知一元二次方程x2-4x-3=0的两根为m,n,则m2-mn+n2= .
25
解析: 根据根与系数的关系可知,m+n=4,mn=-3. m2-mn+n2=m2+n2-mn=(m+n)2-3mn=42-3 ×(-3)=25.故填25.
考点专练
考点六 利用一元二次方程解决实际问题
例5:某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染.请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?若病毒得不到有效控制,3轮感染后,被感染的电脑会不会超过700台?
解析:增长率问题在近年中考试题中频频出现,解决此类问题应掌握增长率是指增长数与基准数的比.
考点专练
解:设每轮感染中平均一台电脑会感染x台电脑,则经过1轮后有(1+x)台被染上病毒,2轮后就有(1+x)2台被感染病毒,依题意,得(1+x)2=81,解得x1=8,x2=-10(舍去).
所以每轮感染中平均一台电脑会感染8台电脑.
由此规律,经过3轮后,有(1+x)3=(1+8)3=729台电脑被感染.
由于729>700,所以若病毒得不到有效控制,3轮感染后,被感染的电脑会超过700台.
考点专练
列一元二次方程解应用题的关键是:找出未知量与已知量之间的联系,从而将实际问题转化为方程模型,要善于将普通语言转化为代数式,在审题时,要特别注意关键词语,如“多少、快、慢、和、差、倍、分、超过、剩余、增加、减少”等等,此外,还要掌握一些常用的公式或特殊的等量关系,如特殊图形的面积公式、行程问题、工程问题、增长率问题中的一些特殊关系等.
方法技巧
https://www.21cnjy.com/help/help_extract.php
单元复习
第二章
一元二次方程
2021-2022学年九年级数学上册同步(北师版)
本
章
知
识
架
构
知
识
专
题
要点梳理
ax2+bx+c=0(a、b、c为常数,a___0).其中ax2是二次项,a是二次项系数,bx是一次项,b是一次项系数,c是常数项.
1.概念:
只含有___未知数,并且未知数的最高次数为___的_____方程.
一、一元二方程的概念
2.一般形式:
1
≠
2
整式
解法 方程类型 注意事项
1.直接开平方法 (1)当方程缺少一次项,即方程ax2+c=0(a≠0,ac<0) (2)形如a(x+n)2=b(a≠0,ab>0)的方程 开方后取值符号是“±”
2.配方法 将二次项系数化为1后,一次项系数为绝对值较小的偶数时,考虑使用配方法:给方程两边同时加上_____________________ (1)在配方过程中,一定要在等号两边同时加上一个_____的数;
(2)将方程的二次项系数化为1后,一次项的正负决定配方后括号里面是加或减
二、一元二次方程的解法
一次项系数一半的平方
相同
要点梳理
解法 方程类型 注意事项
3.公式法 适用于所有一元二次方程,求根公式为x=____________ (1)使用求根公式时,要先把一元二次方程化为一般形式,方程的右边一定要化为________;
(2)将a,b,c代入求根公式时应注意其符号;
(3)若b2-4ac<0,则原方程___________
4.因式分解法 将方程右边化为0后,方程的左边可以提出含有x的公因数,形如x(ax+b)=0或(ax+b)(cx+d)=0 (1)等号右边必须化为0,若不为0,不能用此法;
(2)方程两边含有x的相同因式时,不能约去,以免丢根,如对于一元二次方程(x-2)(x+2)=(x-2),不能两边同时约去x-2,会造成漏解
0
无解
要点梳理
1.b2-4ac>0 一元二次方程有两个________的实数根
2._________ 一元二次方程有两个相等的实数根
3._________ 一元二次方程没有实数根
三、一元二次方程根的判别式
1.一元二次方程ax2+bx+c=0的根的判别式为:b2-4ac.
2.与根的关系
不相等
b2-4ac=0
b2-4ac<0
要点梳理
三、一元二次方程根的判别式
若所给方程的二次项系数含有字母,求字母的取值范围时,应记住一元二次方程二次项系数不为0这一条件.若未指明方程类型,需分情况(二次项系数为0和二次项系数不为0)讨论
3.注意事项
要点梳理
四、一元二次方程的实际应用
①.
②.若起始量为a,平均增长率为x,终止量为b,增长次数为2,则有___________
③.若起始量为a,平均增长率为x,终止量为b,下降次数为2,则有___________
1.平均变化率问题
a(1+x)2=b
a(1-x)2=b
要点梳理
四、一元二次方程的实际应用
①利润=售价-成本.
2.利润问题
②总利润=总售价-总成本.
③总利润=单个利润×总数量.
利润率=
④
要点梳理
四、一元二次方程的实际应用
3.几何问题
①解题时注意联系图形中有关的几何定理、面积和体积公式;
②不容易直接解决的问题可考虑添加辅助线;
③重视数形结合的思想方法
要点梳理
考点专练
考点一 用配方法解方程
例1:用配方法解方程: 3x2 +18x +24 = 0.
解析: 用配方法解一元二次方程,关键的一步是将二次项系数已化为1的方程的两边加上一次项系数一半的平方,转化为(x+m)2=n的形式,当n≥0时,直接开平方求得方程的根.
考点专练
解:方程两边同时除以3,得
x2 + 6x + 8 = 0 .
移项,得 x2 + 6x = -8 ,
配方, 得 (x + 3)2 = 1.
开平方, 得 x + 3 = ±1.
解得 x1 = -2 , x2= -4 .
例1:用配方法解方程: 3x2 +18x +24 = 0.
考点二 用公式法解方程
例2:用公式法解方程:x2-4x-1=0.
解析: 用公式法解方程时应先把一元二次方程化为一般形式,再确定a,b,c的值.
考点专练
根据公式法,我们可以利用b2-4ac的值判断一元二次方程根的情况:当b2-4ac>0时,方程有两个不相等的实数根;当b2-4ac=0时,方程有两个相等的实数根;当b2-4ac<0时,方程无实数根.反之,知道一元二次方程根的情况,也可以判断b2-4ac的符号.
方法技巧
考点三 用因式分解法解方程
例3:用因式分解法解方程:(x -3)2 + 3-x =0.
解析: (1)经过变形后可用提取公因式法分解因式,(2)可直接将方程左边分解因式.
解:(1)原方程变形为 (x-3)2-(x-3)=0,
(x-3)(x-3-1)=0,
即 (x-3)(x-4)=0,
x-3=0 或x-4=0,
∴x1=3,x2=4.
考点专练
考点专练
当一元二次方程的一边为0,而另一边易于分解成两个一次因式的乘积时,我们可以利用因式分解法解一元二次方程.用式子表示:若a·b=0,则a=0或b=0,反之也成立.有时遇到解高次方程时,也可以利用这种方式降次.如x4-16=0,则(x2+4)(x+2)(x-2)=0,其左边是三个因式,其中有一个二次的因式,其余两个是一次的因式.分解因式法把一个一元二次方程化为两个一元一次方程来解,体现了一种“降次”的思想.
方法技巧
考点五 一元二次方程根与系数的关系
例4 已知一元二次方程x2-4x-3=0的两根为m,n,则m2-mn+n2= .
25
解析: 根据根与系数的关系可知,m+n=4,mn=-3. m2-mn+n2=m2+n2-mn=(m+n)2-3mn=42-3 ×(-3)=25.故填25.
考点专练
考点六 利用一元二次方程解决实际问题
例5:某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染.请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?若病毒得不到有效控制,3轮感染后,被感染的电脑会不会超过700台?
解析:增长率问题在近年中考试题中频频出现,解决此类问题应掌握增长率是指增长数与基准数的比.
考点专练
解:设每轮感染中平均一台电脑会感染x台电脑,则经过1轮后有(1+x)台被染上病毒,2轮后就有(1+x)2台被感染病毒,依题意,得(1+x)2=81,解得x1=8,x2=-10(舍去).
所以每轮感染中平均一台电脑会感染8台电脑.
由此规律,经过3轮后,有(1+x)3=(1+8)3=729台电脑被感染.
由于729>700,所以若病毒得不到有效控制,3轮感染后,被感染的电脑会超过700台.
考点专练
列一元二次方程解应用题的关键是:找出未知量与已知量之间的联系,从而将实际问题转化为方程模型,要善于将普通语言转化为代数式,在审题时,要特别注意关键词语,如“多少、快、慢、和、差、倍、分、超过、剩余、增加、减少”等等,此外,还要掌握一些常用的公式或特殊的等量关系,如特殊图形的面积公式、行程问题、工程问题、增长率问题中的一些特殊关系等.
方法技巧
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
