人教版2021--2022九年级(上)数学第二十三章《旋转》单元质量检测试卷B(含解析)
文档属性
| 名称 | 人教版2021--2022九年级(上)数学第二十三章《旋转》单元质量检测试卷B(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-14 06:51:05 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版2021-2022学年九年级(上)第二十三章旋转检测试卷B
(时间120分钟,满分120分)
一、选择题(共10小题;每小题3分,共30分)
1. 如图,将 绕点 按逆时针方向旋转 后得到 ,若 ,则 的度数是 .
A. B. C. D.
2. 《国家宝藏》节目立足于中华文化宝库资源,通过对文物的梳理与总结,演绎文物背后的故事与历史,让更多的观众走进博物馆,让一个个馆藏文物鲜活起来.下面四幅图是我国一些博物馆的标志,其中是中心对称图形的是
A. B.
C. D.
3. 以下四个图案中,是轴对称图形但不是中心对称图形的是
A. B.
C. D.
4. 如图,在方格纸中,将 绕点 按顺时针方向旋转 后得到 ,则下列四个图形中正确的是
A. B.
C. D.
5. 将如图所示的图形绕点 顺时针旋转 得到的图形是
A. B.
C. D.
6. 如图,紫金花图案旋转一定角度后与自身重合,则旋转的角度可能是
A. B. C. D.
7. 如图,在 中,, 与 关于点 对称,连接 ,,当四边形 为矩形时, 的度数为
A. B. C. D.
8. 下列各图中,能由“基本图案”通过旋转变形得到的图形是
A. B.
C. D.
9. 下列选项中不能由图旋转得到的是
A. B.
C. D.
10. 如图,将矩形 绕点 顺时针旋转 后,得到矩形 ,若 ,,连接 ,那么 的长是
A. B. C. D.
二、填空题(共6小题;每小题3分,共18分)
11. 如图,②③④⑤中由图①顺时针旋转 变换而成的是
12. 如图,在正方形网格中,线段 可以看作是线段 经过若干次图形的变化(平移、旋转、轴对称)得到的,写出一种由线段 得到线段 的过程: .
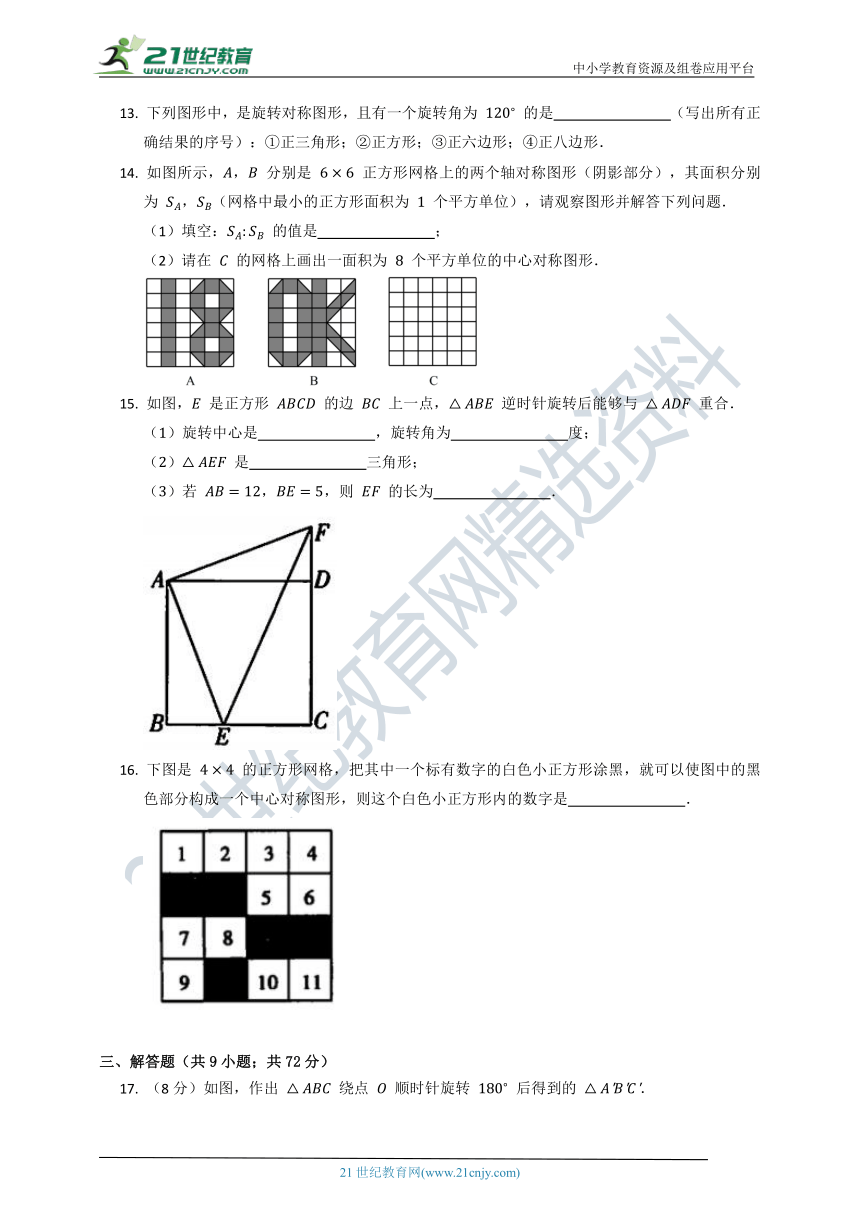
13. 下列图形中,是旋转对称图形,且有一个旋转角为 的是 (写出所有正确结果的序号):①正三角形;②正方形;③正六边形;④正八边形.
14. 如图所示,, 分别是 正方形网格上的两个轴对称图形(阴影部分),其面积分别为 ,(网格中最小的正方形面积为 个平方单位),请观察图形并解答下列问题.
(1)填空: 的值是 ;
(2)请在 的网格上画出一面积为 个平方单位的中心对称图形.
15. 如图, 是正方形 的边 上一点, 逆时针旋转后能够与 重合.
()旋转中心是 ,旋转角为 度;
() 是 三角形;
()若 ,,则 的长为 .
16. 下图是 的正方形网格,把其中一个标有数字的白色小正方形涂黑,就可以使图中的黑色部分构成一个中心对称图形,则这个白色小正方形内的数字是 .
三、解答题(共9小题;共72分)
17. (8分)如图,作出 绕点 顺时针旋转 后得到的 .
18. (6分)画出一个旋转角为 的旋转对称图形.
19. (8分)如果公园里的草坪是如图所示的形状,你能否只修一条笔直的小路就将这块草坪分成面积相等的两部分 请画出小路的位置.
20. (8分)如图,四边形 与四边形 关于某点对称,找出它们的对称中心.
21. (8分)如图, 张扑克牌放在桌上.现将其中的某一张在原地旋转 ,发现旋转后在桌上看到的牌中的图形和原先一模一样.旋转的是哪一张牌
22. (8分)如图,在由边长为 个单位长度的小正方形组成的网格中,给出了以格点(网格线的交点)为端点的线段 ,线段 在网格线上.
()画出线段 关于线段 所在直线对称的线段 (点 , 分别为 , 的对应点);
()将线段 绕点 顺时针旋转 得到线段 ,画出线段 .
23. (10分)如图,在等边 中,点 是线段 上一点.作射线 ,点 关于射线 的对称点为 .连接 并延长,交射线 于点 .
(1)设 ,用 表示 的度数;
(2)用等式表示线段 ,, 之间的数量关系,并证明.
24. (8分)如图,四边形 是正方形, 是等边三角形, 是正方形 对角线 (不含点 )上任意一点,将线段 绕点 逆时针旋转 得到 ,连接 ,.求证:.
25. (8分)如图,线段 与 成中心对称.
(1)请作图找出对称中心 ;
(2)连接 ,,则四边形 是 四边形.
答案
第一部分
1. B
2. C
3. A
4. B 【解析】A选项是原图形的对称图形,故A不正确;
B选项是 绕点 按顺时针方向旋转 后得到 ,故B正确;
C选项旋转后的对应点错误,即形状发生了改变,故C不正确;
D选项是按逆时针方向旋转 ,故D不正确.
5. D
6. C
7. C
8. A
9. C
10. D
【解析】 四边形 为矩形,
,在 中,
,,
,
矩形 绕点 顺时针旋转 后,得到矩形 ,
,,
为等腰直角三角形,
.
第二部分
11. ④
12. 将线段 绕点 逆时针旋转 ,再向左平移 个单位长度
13. ①③
14. ,如图:
15. 点 ,,等腰直角,
16.
【解析】如图,
把标有数字 的白色小正方形涂黑,就可以使图中的黑色部分构成一个中心对称图形.
第三部分
17. 如答图, 即为所求.
18. 略.
19. 能,如图,
小路 即为所求.
20. 如图,连接 , 交于点 ,点 即为所求.
21. 第()张.
22. ()如图,线段 即为所求.
()如图,线段 即为所求.
23. (1) 连接 .
点 关于射线 的对称点为 ,
,,
是等边三角形,
,,
,,
,
.
【解析】另解:借助圆.
(2) .
证明:如图,作 交 于点 ,连接 ,
,,
,
是等边三角形.
,
是等边三角形,
,,
,
在 和 中,
,
,
点 关于射线 的对称点为 ,
,
,
.
【解析】另一种证法:作 交 的延长线于点 ,连接 .
24. 是等边三角形,
,,
根据旋转的性质,得 ,,
,
,
四边形 是正方形,
,,
,,
在 和 中,
,
.
25. (1) 连接 ,, 与 的交点就是点 .
(2) 平行
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版2021-2022学年九年级(上)第二十三章旋转检测试卷B
(时间120分钟,满分120分)
一、选择题(共10小题;每小题3分,共30分)
1. 如图,将 绕点 按逆时针方向旋转 后得到 ,若 ,则 的度数是 .
A. B. C. D.
2. 《国家宝藏》节目立足于中华文化宝库资源,通过对文物的梳理与总结,演绎文物背后的故事与历史,让更多的观众走进博物馆,让一个个馆藏文物鲜活起来.下面四幅图是我国一些博物馆的标志,其中是中心对称图形的是
A. B.
C. D.
3. 以下四个图案中,是轴对称图形但不是中心对称图形的是
A. B.
C. D.
4. 如图,在方格纸中,将 绕点 按顺时针方向旋转 后得到 ,则下列四个图形中正确的是
A. B.
C. D.
5. 将如图所示的图形绕点 顺时针旋转 得到的图形是
A. B.
C. D.
6. 如图,紫金花图案旋转一定角度后与自身重合,则旋转的角度可能是
A. B. C. D.
7. 如图,在 中,, 与 关于点 对称,连接 ,,当四边形 为矩形时, 的度数为
A. B. C. D.
8. 下列各图中,能由“基本图案”通过旋转变形得到的图形是
A. B.
C. D.
9. 下列选项中不能由图旋转得到的是
A. B.
C. D.
10. 如图,将矩形 绕点 顺时针旋转 后,得到矩形 ,若 ,,连接 ,那么 的长是
A. B. C. D.
二、填空题(共6小题;每小题3分,共18分)
11. 如图,②③④⑤中由图①顺时针旋转 变换而成的是
12. 如图,在正方形网格中,线段 可以看作是线段 经过若干次图形的变化(平移、旋转、轴对称)得到的,写出一种由线段 得到线段 的过程: .
13. 下列图形中,是旋转对称图形,且有一个旋转角为 的是 (写出所有正确结果的序号):①正三角形;②正方形;③正六边形;④正八边形.
14. 如图所示,, 分别是 正方形网格上的两个轴对称图形(阴影部分),其面积分别为 ,(网格中最小的正方形面积为 个平方单位),请观察图形并解答下列问题.
(1)填空: 的值是 ;
(2)请在 的网格上画出一面积为 个平方单位的中心对称图形.
15. 如图, 是正方形 的边 上一点, 逆时针旋转后能够与 重合.
()旋转中心是 ,旋转角为 度;
() 是 三角形;
()若 ,,则 的长为 .
16. 下图是 的正方形网格,把其中一个标有数字的白色小正方形涂黑,就可以使图中的黑色部分构成一个中心对称图形,则这个白色小正方形内的数字是 .
三、解答题(共9小题;共72分)
17. (8分)如图,作出 绕点 顺时针旋转 后得到的 .
18. (6分)画出一个旋转角为 的旋转对称图形.
19. (8分)如果公园里的草坪是如图所示的形状,你能否只修一条笔直的小路就将这块草坪分成面积相等的两部分 请画出小路的位置.
20. (8分)如图,四边形 与四边形 关于某点对称,找出它们的对称中心.
21. (8分)如图, 张扑克牌放在桌上.现将其中的某一张在原地旋转 ,发现旋转后在桌上看到的牌中的图形和原先一模一样.旋转的是哪一张牌
22. (8分)如图,在由边长为 个单位长度的小正方形组成的网格中,给出了以格点(网格线的交点)为端点的线段 ,线段 在网格线上.
()画出线段 关于线段 所在直线对称的线段 (点 , 分别为 , 的对应点);
()将线段 绕点 顺时针旋转 得到线段 ,画出线段 .
23. (10分)如图,在等边 中,点 是线段 上一点.作射线 ,点 关于射线 的对称点为 .连接 并延长,交射线 于点 .
(1)设 ,用 表示 的度数;
(2)用等式表示线段 ,, 之间的数量关系,并证明.
24. (8分)如图,四边形 是正方形, 是等边三角形, 是正方形 对角线 (不含点 )上任意一点,将线段 绕点 逆时针旋转 得到 ,连接 ,.求证:.
25. (8分)如图,线段 与 成中心对称.
(1)请作图找出对称中心 ;
(2)连接 ,,则四边形 是 四边形.
答案
第一部分
1. B
2. C
3. A
4. B 【解析】A选项是原图形的对称图形,故A不正确;
B选项是 绕点 按顺时针方向旋转 后得到 ,故B正确;
C选项旋转后的对应点错误,即形状发生了改变,故C不正确;
D选项是按逆时针方向旋转 ,故D不正确.
5. D
6. C
7. C
8. A
9. C
10. D
【解析】 四边形 为矩形,
,在 中,
,,
,
矩形 绕点 顺时针旋转 后,得到矩形 ,
,,
为等腰直角三角形,
.
第二部分
11. ④
12. 将线段 绕点 逆时针旋转 ,再向左平移 个单位长度
13. ①③
14. ,如图:
15. 点 ,,等腰直角,
16.
【解析】如图,
把标有数字 的白色小正方形涂黑,就可以使图中的黑色部分构成一个中心对称图形.
第三部分
17. 如答图, 即为所求.
18. 略.
19. 能,如图,
小路 即为所求.
20. 如图,连接 , 交于点 ,点 即为所求.
21. 第()张.
22. ()如图,线段 即为所求.
()如图,线段 即为所求.
23. (1) 连接 .
点 关于射线 的对称点为 ,
,,
是等边三角形,
,,
,,
,
.
【解析】另解:借助圆.
(2) .
证明:如图,作 交 于点 ,连接 ,
,,
,
是等边三角形.
,
是等边三角形,
,,
,
在 和 中,
,
,
点 关于射线 的对称点为 ,
,
,
.
【解析】另一种证法:作 交 的延长线于点 ,连接 .
24. 是等边三角形,
,,
根据旋转的性质,得 ,,
,
,
四边形 是正方形,
,,
,,
在 和 中,
,
.
25. (1) 连接 ,, 与 的交点就是点 .
(2) 平行
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
