苏科版八年级数学上册第一章 数学活动 关于三角形全等的条件课件(15张ppt)
文档属性
| 名称 | 苏科版八年级数学上册第一章 数学活动 关于三角形全等的条件课件(15张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 261.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-14 13:28:47 | ||
图片预览





文档简介
(共15张PPT)
数学活动 关于三角形全等的条件
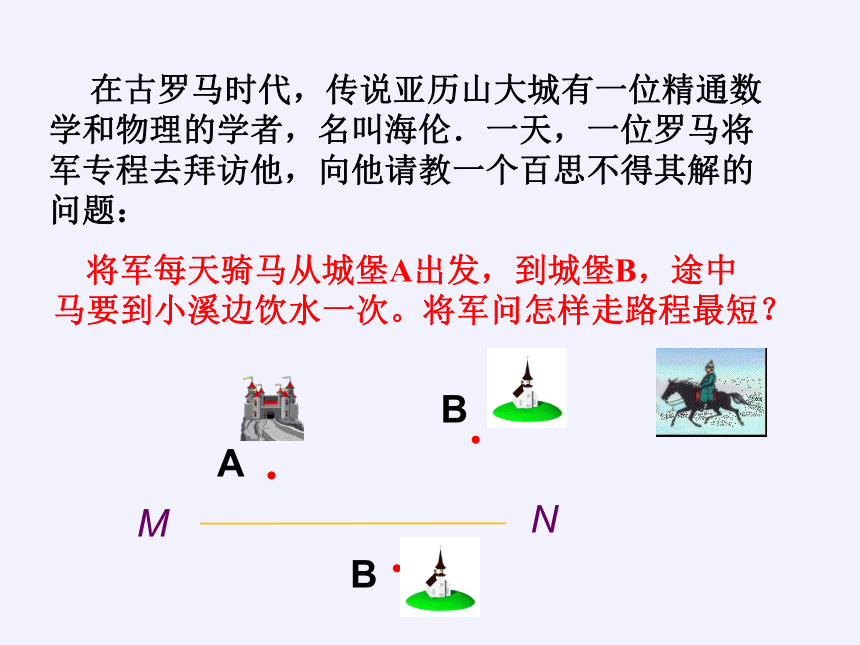
在古罗马时代,传说亚历山大城有一位精通数学和物理的学者,名叫海伦.一天,一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题:
将军每天骑马从城堡A出发,到城堡B,途中马要到小溪边饮水一次。将军问怎样走路程最短?
B
A
M
N
B
由“将军饮马”问题引出的最值问题
如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上的一动点,DN+MN的最小值为 .
6
8
10
10
练习1:
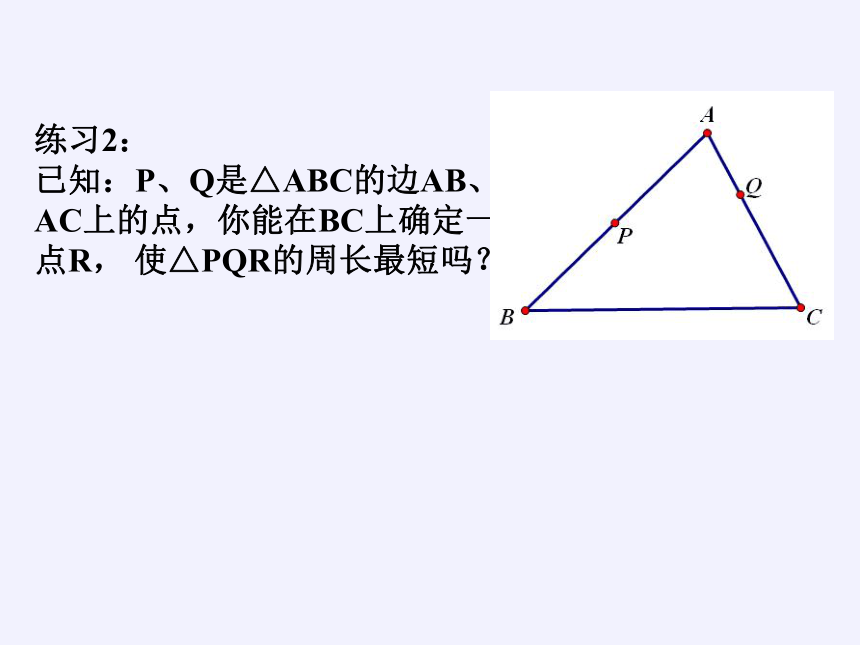
练习2:
已知:P、Q是△ABC的边AB、 AC上的点,你能在BC上确定一点R, 使△PQR的周长最短吗?
如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为_________cm.
练习3:
话说将军带队出去打仗,驻扎在A地休息,他先牵马去草地 OM吃草,再牵马去河边ON喝水, 最后回到驻地A.问:这位将军怎样走路程最短?
草地
河边
.驻地A
O
M
N
M
N
O
●
A
变式1:
如图,∠AOB=30°,∠AOB内有一定点P,且OP=10,在OA上有一点Q,OB上有一点R。若△PQR周长最小,则最小周长是多少?
练习4:
不久,将军凯旋而归,再次来到之前的驻扎地休息。建了马厩A,搭了帐篷B。他从马厩牵出马,先到草地边某一处牧马,再到河边饮马,然后再回到帐篷,请问将军怎样走路程最短?
O
N
M
变式2:
如图,在x轴上找一点C,在y轴上找一点D,使AD+CD+BC最小,并求直线CD的解析式及点C、D的坐标。
练习5:
这节课,你有哪些收获?
课堂小结
1.知识方面:
课堂小结
两点之间线段最短
2.解决方法:
轴对称变换
3.数学思想:
化归思想:同侧转化为异侧;化折为直;立体图形转化为平面图形
分类思想
将军又遇到了新的问题:将军从军营A去军营B的路上除了饮马外,还要牵马在河岸散步200米,这个时候如何行走的路线最短呢?
拓展模型:
思考题
如图5,在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.若E、F为边OA上的两个动点(E在F左侧),且EF=2,当四边形CDEF的周长最小时,点E、F的坐标分别为 、 .
图5
D’
Q
E
[想一想]
这个题跟刚刚的过桥问题有什么联系和区别?
如果能把这个题看成是过桥问题的话,请问桥是指哪一段?
F
(1/3,0)
(7/3,0)
谢 谢
数学活动 关于三角形全等的条件
在古罗马时代,传说亚历山大城有一位精通数学和物理的学者,名叫海伦.一天,一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题:
将军每天骑马从城堡A出发,到城堡B,途中马要到小溪边饮水一次。将军问怎样走路程最短?
B
A
M
N
B
由“将军饮马”问题引出的最值问题
如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上的一动点,DN+MN的最小值为 .
6
8
10
10
练习1:
练习2:
已知:P、Q是△ABC的边AB、 AC上的点,你能在BC上确定一点R, 使△PQR的周长最短吗?
如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为_________cm.
练习3:
话说将军带队出去打仗,驻扎在A地休息,他先牵马去草地 OM吃草,再牵马去河边ON喝水, 最后回到驻地A.问:这位将军怎样走路程最短?
草地
河边
.驻地A
O
M
N
M
N
O
●
A
变式1:
如图,∠AOB=30°,∠AOB内有一定点P,且OP=10,在OA上有一点Q,OB上有一点R。若△PQR周长最小,则最小周长是多少?
练习4:
不久,将军凯旋而归,再次来到之前的驻扎地休息。建了马厩A,搭了帐篷B。他从马厩牵出马,先到草地边某一处牧马,再到河边饮马,然后再回到帐篷,请问将军怎样走路程最短?
O
N
M
变式2:
如图,在x轴上找一点C,在y轴上找一点D,使AD+CD+BC最小,并求直线CD的解析式及点C、D的坐标。
练习5:
这节课,你有哪些收获?
课堂小结
1.知识方面:
课堂小结
两点之间线段最短
2.解决方法:
轴对称变换
3.数学思想:
化归思想:同侧转化为异侧;化折为直;立体图形转化为平面图形
分类思想
将军又遇到了新的问题:将军从军营A去军营B的路上除了饮马外,还要牵马在河岸散步200米,这个时候如何行走的路线最短呢?
拓展模型:
思考题
如图5,在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.若E、F为边OA上的两个动点(E在F左侧),且EF=2,当四边形CDEF的周长最小时,点E、F的坐标分别为 、 .
图5
D’
Q
E
[想一想]
这个题跟刚刚的过桥问题有什么联系和区别?
如果能把这个题看成是过桥问题的话,请问桥是指哪一段?
F
(1/3,0)
(7/3,0)
谢 谢
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
