2021-2022学年华东师大版数学九年级上学期 23.3.3相似三角形的性质课件(22张)
文档属性
| 名称 | 2021-2022学年华东师大版数学九年级上学期 23.3.3相似三角形的性质课件(22张) |  | |
| 格式 | zip | ||
| 文件大小 | 903.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-14 11:45:23 | ||
图片预览






文档简介
(共22张PPT)
23.3相似三角形
23.3.3相似三角形的性质
学习目标
1.掌握相似三角形的性质;(重点)
2.经历探索相似三角形性质的过程.(难点)
回顾与思考
(1)什么叫相似三角形?
对应角相等、对应边成比例的三角形,叫做相似三角形.
(2)如何判定两个三角形相似?
①两个角对应相等;
②两边对应成比例,且夹角相等;
③三边对应成比例.
①相似三角形的对应角_____________
②相似三角形的对应边______________
(3)相似三角形有何性质?
A
B
C
A/
B/
C/
回顾与思考
一个三角形有三条重要线段:________________
思考:如果两个三角形相似,
那么这些对应线段有什么关系呢?
高、中线、角平分线
A
B
C
A/
B/
C/
探究: 相似三角形对应线段(高、中线、角平分线)的比
如图,△ ∽△ABC,相似比为k,分别作BC, 上的高AD, .
求 的值
证明:
∵△ ∽△ABC,
∴ ∠B′= ∠B.
又∵ =∠ADB =90°,
∴△ ∽△ABD. (两角对应相等的两个三角形相似)
从而
(相似三角形的对应边成比例)
新知归纳
推论:
相似三角形对应边上的中线,对应角的平分线的比也等于相似比.
一般地,我们有:
相似三角形对应线段的比等于相似比.
相似三角形的性质定理1:
相似三角形的对应边上的高的比等于相似比.
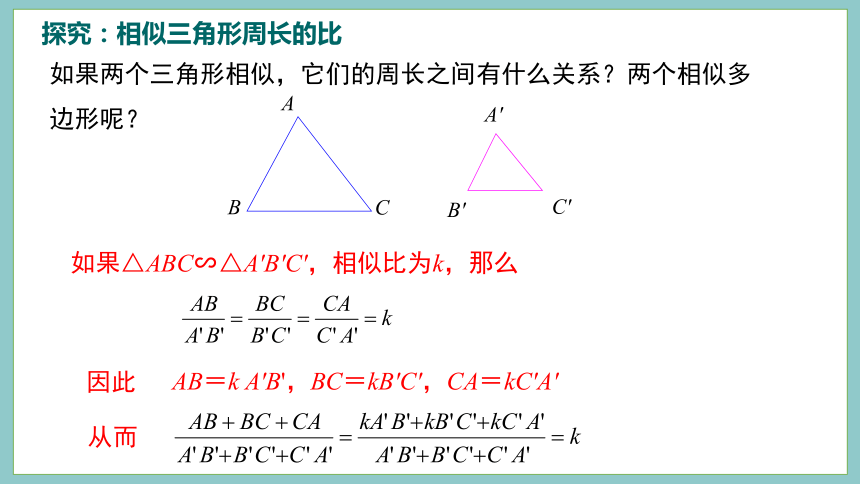
探究:相似三角形周长的比
如果两个三角形相似,它们的周长之间有什么关系?两个相似多边形呢?
A
B
C
A'
B'
C'
如果△ABC∽△A'B'C',相似比为k,那么
因此
AB=k A'B',BC=kB'C',CA=kC'A'
从而
新知归纳
相似三角形周长的比等于相似比.
相似多边形周长的比等于相似比.
同理得:
1.若两个相似三角形的对应中线之比为3∶5,则它们对应角平分线的比为________
2.(沈阳中考)已知△ABC∽△A′B′C′,AD和A′D′是它们的对应中线,若AD=10,A′D′=6,则△ABC与△A′B′C′的周长比是_________
3.已知△FHB∽△EAD,它们的周长分别为30和15,且FH=6,则EA的长为_________
4.两个相似三角形的对应高之比为1∶2,那么它们的对应中线之比为_________.
练习1
1∶2
3∶5
5∶3
3
探究:相似三角形面积的比
如图,△ABC∽△A' B' C' ,相似比为k,它们的面积比是多少?
A
B
C
A'
B'
C'
D'
D
解:如图,分别作出△ABC和△A' B' C'
的高AD和A' D' .
∵ ∠ADB =∠A' D' B' ,∠B=∠B'
∴ △ADB∽△A' D' B'
新知归纳
相似三角形面积的比等于相似比的平方.
猜测:四边形ABCD相似于四边形A′B′C′D′,相似比为k,它们面积的比是多少?
相似多边形面积比等于相似比的平方.
A
B
C
A′
B′
C′
D
D′
练习2
C
A
2.如图,在平行四边形ABCD中,E是DC上的点,DE∶EC=3∶2,连结AE交BD于点F,则△DEF与△BAF的面积之比为( )
A.2∶5 B.3∶5 C.9∶25 D.4∶25
C
第3题图
第2题图
4.如图,在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D,△ABC的周长是24,面积是48,求△DEF的周长和面积.
A
B
C
D
E
F
∴ △DEF∽△ABC,相似比为
又 ∠D=∠A
解:在△ABC和△DEF中,
∵ AB=2DE,AC=2DF
∴
∴△DEF的周长= △ABC的周长,
△DEF的周长=12.
练习2
当堂练习
1.判断
(1)一个三角形的各边长扩大为原来的5倍,这个三角形的周长也扩大为原来的5倍;
(2)一个四边形的各边长扩大为原来的9倍,这个四边形的面积也扩大为原来的9倍.
一个三角形各边扩大为原来9倍,相似比为1:9
边长扩大9倍四边形=81倍原四边形的的面积
一个三角形各边扩大为原来5倍,相似比为1:5
扩大5倍周长=5×原周长
当堂练习
当堂练习
当堂练习
当堂练习
当堂练习
5.如图,在 ABCD中,AB=10,AD=15,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G,若BG=8,则△CEF的周长为
当堂练习
课堂小结
1.相似三角形的对应高,中线,角平分线的比等于相似比.
一般地,我们有:
相似三角形对应线段的比等于相似比.
2.相似三角形周长的比等于相似比;
相似多边形周长的比等于相似比.
3.相似三角形面积的比等于相似比的平方;
相似多边形面积的比等于相似比的平方.
完毕·感谢
The user can perform the presentation on a projector or computer, and the powerpoint can be printed out and made into film.
23.3相似三角形
23.3.3相似三角形的性质
学习目标
1.掌握相似三角形的性质;(重点)
2.经历探索相似三角形性质的过程.(难点)
回顾与思考
(1)什么叫相似三角形?
对应角相等、对应边成比例的三角形,叫做相似三角形.
(2)如何判定两个三角形相似?
①两个角对应相等;
②两边对应成比例,且夹角相等;
③三边对应成比例.
①相似三角形的对应角_____________
②相似三角形的对应边______________
(3)相似三角形有何性质?
A
B
C
A/
B/
C/
回顾与思考
一个三角形有三条重要线段:________________
思考:如果两个三角形相似,
那么这些对应线段有什么关系呢?
高、中线、角平分线
A
B
C
A/
B/
C/
探究: 相似三角形对应线段(高、中线、角平分线)的比
如图,△ ∽△ABC,相似比为k,分别作BC, 上的高AD, .
求 的值
证明:
∵△ ∽△ABC,
∴ ∠B′= ∠B.
又∵ =∠ADB =90°,
∴△ ∽△ABD. (两角对应相等的两个三角形相似)
从而
(相似三角形的对应边成比例)
新知归纳
推论:
相似三角形对应边上的中线,对应角的平分线的比也等于相似比.
一般地,我们有:
相似三角形对应线段的比等于相似比.
相似三角形的性质定理1:
相似三角形的对应边上的高的比等于相似比.
探究:相似三角形周长的比
如果两个三角形相似,它们的周长之间有什么关系?两个相似多边形呢?
A
B
C
A'
B'
C'
如果△ABC∽△A'B'C',相似比为k,那么
因此
AB=k A'B',BC=kB'C',CA=kC'A'
从而
新知归纳
相似三角形周长的比等于相似比.
相似多边形周长的比等于相似比.
同理得:
1.若两个相似三角形的对应中线之比为3∶5,则它们对应角平分线的比为________
2.(沈阳中考)已知△ABC∽△A′B′C′,AD和A′D′是它们的对应中线,若AD=10,A′D′=6,则△ABC与△A′B′C′的周长比是_________
3.已知△FHB∽△EAD,它们的周长分别为30和15,且FH=6,则EA的长为_________
4.两个相似三角形的对应高之比为1∶2,那么它们的对应中线之比为_________.
练习1
1∶2
3∶5
5∶3
3
探究:相似三角形面积的比
如图,△ABC∽△A' B' C' ,相似比为k,它们的面积比是多少?
A
B
C
A'
B'
C'
D'
D
解:如图,分别作出△ABC和△A' B' C'
的高AD和A' D' .
∵ ∠ADB =∠A' D' B' ,∠B=∠B'
∴ △ADB∽△A' D' B'
新知归纳
相似三角形面积的比等于相似比的平方.
猜测:四边形ABCD相似于四边形A′B′C′D′,相似比为k,它们面积的比是多少?
相似多边形面积比等于相似比的平方.
A
B
C
A′
B′
C′
D
D′
练习2
C
A
2.如图,在平行四边形ABCD中,E是DC上的点,DE∶EC=3∶2,连结AE交BD于点F,则△DEF与△BAF的面积之比为( )
A.2∶5 B.3∶5 C.9∶25 D.4∶25
C
第3题图
第2题图
4.如图,在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D,△ABC的周长是24,面积是48,求△DEF的周长和面积.
A
B
C
D
E
F
∴ △DEF∽△ABC,相似比为
又 ∠D=∠A
解:在△ABC和△DEF中,
∵ AB=2DE,AC=2DF
∴
∴△DEF的周长= △ABC的周长,
△DEF的周长=12.
练习2
当堂练习
1.判断
(1)一个三角形的各边长扩大为原来的5倍,这个三角形的周长也扩大为原来的5倍;
(2)一个四边形的各边长扩大为原来的9倍,这个四边形的面积也扩大为原来的9倍.
一个三角形各边扩大为原来9倍,相似比为1:9
边长扩大9倍四边形=81倍原四边形的的面积
一个三角形各边扩大为原来5倍,相似比为1:5
扩大5倍周长=5×原周长
当堂练习
当堂练习
当堂练习
当堂练习
当堂练习
5.如图,在 ABCD中,AB=10,AD=15,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G,若BG=8,则△CEF的周长为
当堂练习
课堂小结
1.相似三角形的对应高,中线,角平分线的比等于相似比.
一般地,我们有:
相似三角形对应线段的比等于相似比.
2.相似三角形周长的比等于相似比;
相似多边形周长的比等于相似比.
3.相似三角形面积的比等于相似比的平方;
相似多边形面积的比等于相似比的平方.
完毕·感谢
The user can perform the presentation on a projector or computer, and the powerpoint can be printed out and made into film.
