2021-2022学年人教版数学八年级上册13.1 轴对称课件(20张)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册13.1 轴对称课件(20张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-14 11:48:40 | ||
图片预览




文档简介
(共20张PPT)
13.1.1 轴对称
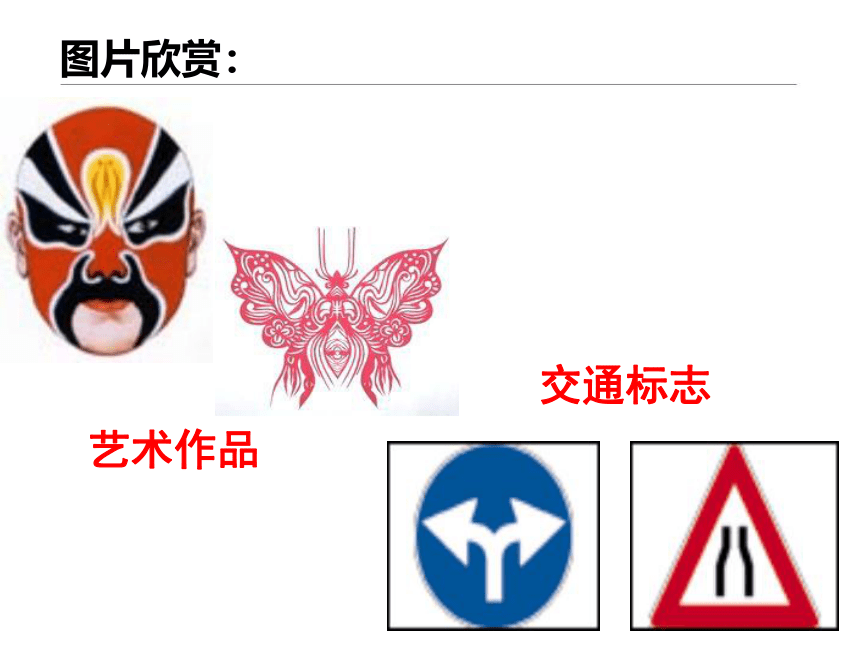
图片欣赏:
艺术作品
交通标志
思考:
你能发现它们有什么共
同的特点吗?
仔细观察:
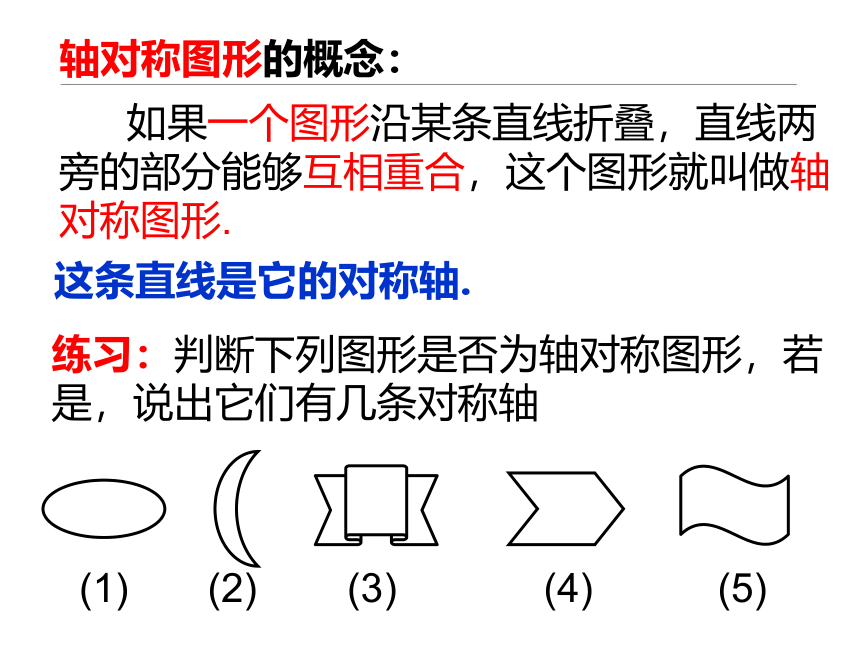
轴对称图形的概念:
如果一个图形沿某条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形.
这条直线是它的对称轴.
练习:判断下列图形是否为轴对称图形,若是,说出它们有几条对称轴
(1) (2) (3) (4) (5)
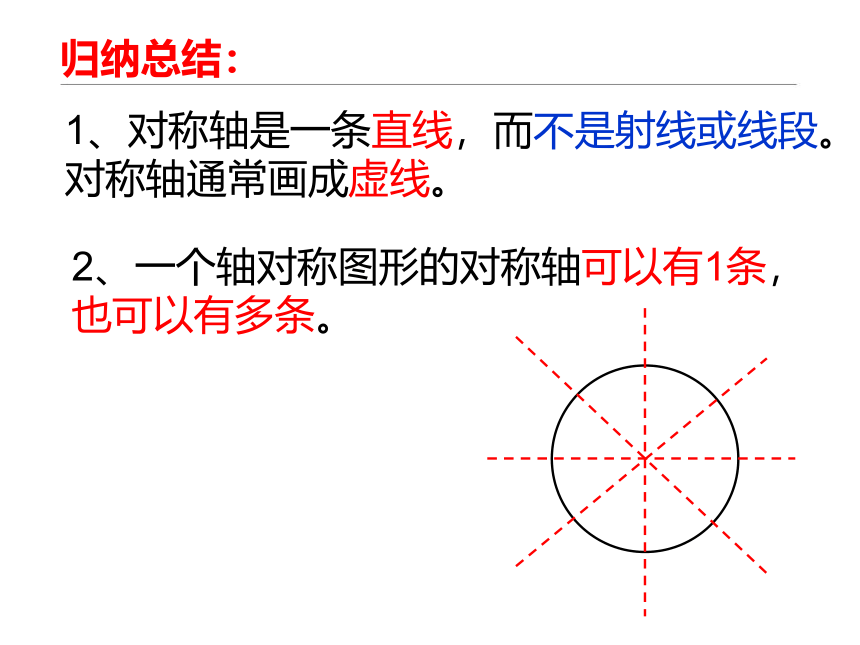
归纳总结:
1、对称轴是一条直线,而不是射线或线段。
对称轴通常画成虚线。
2、一个轴对称图形的对称轴可以有1条,
也可以有多条。
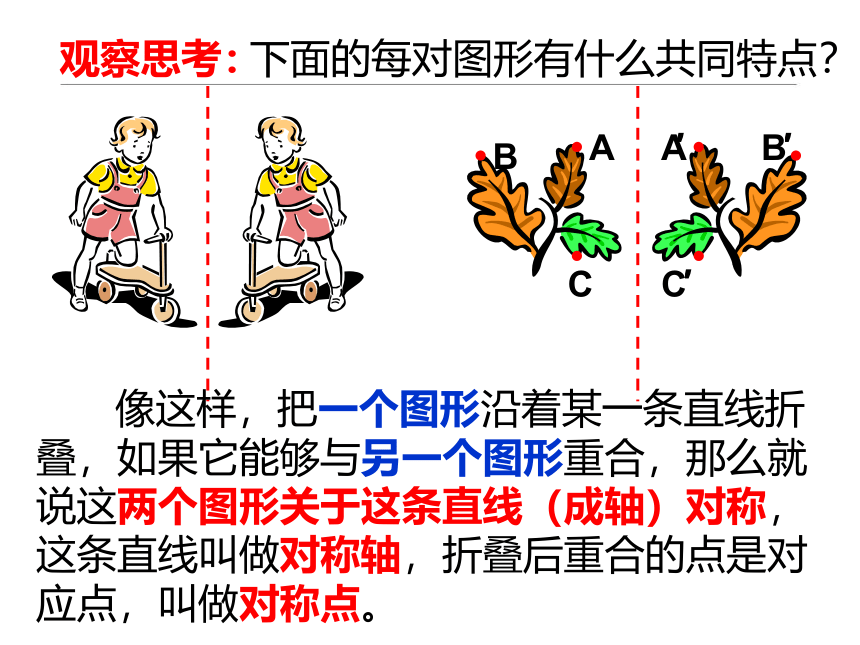
观察思考:
下面的每对图形有什么共同特点?
A
A
′
B
B
′
C
C
′
像这样,把一个图形沿着某一条直线折
叠,如果它能够与另一个图形重合,那么就
说这两个图形关于这条直线(成轴)对称,
这条直线叫做对称轴,折叠后重合的点是对
应点,叫做对称点。
轴对称和轴对称图形的区别:
名称
关系
区
别
意义不同
对象不同
对称轴的
位置不同
对称轴的
数量不同
轴对称
轴对称图形
两个图形间的对
称关系
具有特殊形状的
图形
两个图形
一个图形
在两个图形之间
过图形的某条直线
只有一条
不一定只有一条
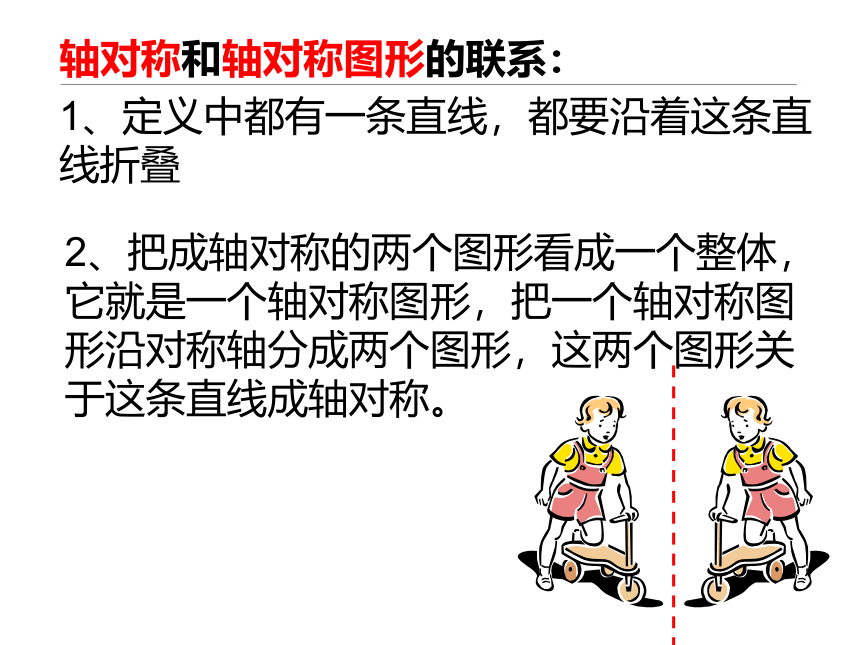
轴对称和轴对称图形的联系:
1、定义中都有一条直线,都要沿着这条直
线折叠
2、把成轴对称的两个图形看成一个整体,
它就是一个轴对称图形,把一个轴对称图
形沿对称轴分成两个图形,这两个图形关
于这条直线成轴对称。
镜面对称:
如图,是在一面镜子中看到的一个算式,
该算式的实际情况是怎样的?
水面对称:
一辆汽车的车牌在水中的倒影如图所示,
你能确定该车车牌的号码吗?
思考:
如图,△ABC和△A B C 关于直线MN
对称,点A ,B ,C ,分别是点A,B,C
的对称点,线段AA ,BB ,CC 与直线MN
有什么关系?
′
′
′
′
′
′
′
′
′
A
B
C
C
A
B
′
′
′
M
N
P
线段垂直平分线的定义:
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线。
A
B
M
N
P
几何语言:
(1)∵PA=PB,MN⊥AB
∴MN是线段AB的垂直平分线
(2)∵ MN是线段AB的垂直平分线
∴ PA=PB,MN⊥AB
轴对称的性质:
如果两个图形关于某条直线对称,那
么对称轴是任何一对对应点所连线段的垂直平分线.
A
B
C
C
A
B
′
′
′
M
N
P
类似地,轴对称
图形的对称轴,
是任何一对对应
点所连线段的垂
直平分线.
练习:
1、下列几何图形中:①线段;②角;③直角三角形;④半圆,其中一定是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
练习:
2、下列说法错误的是( )
A.关于某条直线对称的两个三角形一定全等 B.轴对称图形至少有一条对称轴
C.全等三角形一定能关于某条直线对称 D.角是关于它的平分线所在的直线对称的图形
练习:
3、如图是一个风筝的图案,它是轴对称图形,量得∠B=30°,则∠E的大小为( )
A.30° B.35°
C.40° D.45°
练习:
4、如图,直线m是五边形ABCDE的对称轴,其中∠A=130°,∠B=110°,则∠BCD的度数是( )
A.40° B.50° C.60° D.70°
练习:
5、正五角星的对称轴有__________条
6、小强站在镜子前,从镜子中看到镜子对面墙上挂着的电子表其度数如图所示,则电子表的实际时刻是______________
谢谢!
13.1.1 轴对称
图片欣赏:
艺术作品
交通标志
思考:
你能发现它们有什么共
同的特点吗?
仔细观察:
轴对称图形的概念:
如果一个图形沿某条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形.
这条直线是它的对称轴.
练习:判断下列图形是否为轴对称图形,若是,说出它们有几条对称轴
(1) (2) (3) (4) (5)
归纳总结:
1、对称轴是一条直线,而不是射线或线段。
对称轴通常画成虚线。
2、一个轴对称图形的对称轴可以有1条,
也可以有多条。
观察思考:
下面的每对图形有什么共同特点?
A
A
′
B
B
′
C
C
′
像这样,把一个图形沿着某一条直线折
叠,如果它能够与另一个图形重合,那么就
说这两个图形关于这条直线(成轴)对称,
这条直线叫做对称轴,折叠后重合的点是对
应点,叫做对称点。
轴对称和轴对称图形的区别:
名称
关系
区
别
意义不同
对象不同
对称轴的
位置不同
对称轴的
数量不同
轴对称
轴对称图形
两个图形间的对
称关系
具有特殊形状的
图形
两个图形
一个图形
在两个图形之间
过图形的某条直线
只有一条
不一定只有一条
轴对称和轴对称图形的联系:
1、定义中都有一条直线,都要沿着这条直
线折叠
2、把成轴对称的两个图形看成一个整体,
它就是一个轴对称图形,把一个轴对称图
形沿对称轴分成两个图形,这两个图形关
于这条直线成轴对称。
镜面对称:
如图,是在一面镜子中看到的一个算式,
该算式的实际情况是怎样的?
水面对称:
一辆汽车的车牌在水中的倒影如图所示,
你能确定该车车牌的号码吗?
思考:
如图,△ABC和△A B C 关于直线MN
对称,点A ,B ,C ,分别是点A,B,C
的对称点,线段AA ,BB ,CC 与直线MN
有什么关系?
′
′
′
′
′
′
′
′
′
A
B
C
C
A
B
′
′
′
M
N
P
线段垂直平分线的定义:
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线。
A
B
M
N
P
几何语言:
(1)∵PA=PB,MN⊥AB
∴MN是线段AB的垂直平分线
(2)∵ MN是线段AB的垂直平分线
∴ PA=PB,MN⊥AB
轴对称的性质:
如果两个图形关于某条直线对称,那
么对称轴是任何一对对应点所连线段的垂直平分线.
A
B
C
C
A
B
′
′
′
M
N
P
类似地,轴对称
图形的对称轴,
是任何一对对应
点所连线段的垂
直平分线.
练习:
1、下列几何图形中:①线段;②角;③直角三角形;④半圆,其中一定是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
练习:
2、下列说法错误的是( )
A.关于某条直线对称的两个三角形一定全等 B.轴对称图形至少有一条对称轴
C.全等三角形一定能关于某条直线对称 D.角是关于它的平分线所在的直线对称的图形
练习:
3、如图是一个风筝的图案,它是轴对称图形,量得∠B=30°,则∠E的大小为( )
A.30° B.35°
C.40° D.45°
练习:
4、如图,直线m是五边形ABCDE的对称轴,其中∠A=130°,∠B=110°,则∠BCD的度数是( )
A.40° B.50° C.60° D.70°
练习:
5、正五角星的对称轴有__________条
6、小强站在镜子前,从镜子中看到镜子对面墙上挂着的电子表其度数如图所示,则电子表的实际时刻是______________
谢谢!
