2021—2022学年人教版数学七年级上册1.5.1 有理数的乘方(1)课件(20张)
文档属性
| 名称 | 2021—2022学年人教版数学七年级上册1.5.1 有理数的乘方(1)课件(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 259.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-14 11:49:28 | ||
图片预览








文档简介
(共20张PPT)
1.5.1 有理数的乘方(1)
教学目标
1.理解有理数乘方的意义,了解幂,乘方,底数,指数等相关概念。
2.掌握有理数乘方的符号法则以及相关性质,能正确进行有理数的乘方的运算。
3.培养学生观察,归纳,分析,思考,概括的能力。
如图,一正方形的边长为3cm,则它的面积为________平方厘米;记作_____,读作_ _ ___,或者是_____。
一正方体的棱长为4cm, 则它的体积为___________立方厘米;记作_____,读作_____,或者是_____。
4×4×4
3×3
3
4
情境导入
3的平方
3的2次方
4的立方
4的3次方
43
4×4×4 记作:
一般的,任意多个相同的有理数相乘,我们如何去简化表示呢?
相同因数的乘法如何简化
3×3记作:
32
43
3是______;
2是______
4是____________,
3是___________
相同的因数
因数的个数
相同的因数
因数的个数
4×4×4×4×4,可以表示为__________,
读作_________,
× × × ,可以表示为__________,
读作 _________,
7×7×7×7×7×7×7,可以表示为__________,
读作_________,1.2×1.2×1.2×1.2×1.2×1.2×1.2,
可以表示为__________,读作_________,
类比上面的形式
(1.2)7
77
4
45
1.2的7次方
7的7次方
的4次方
4的5次方
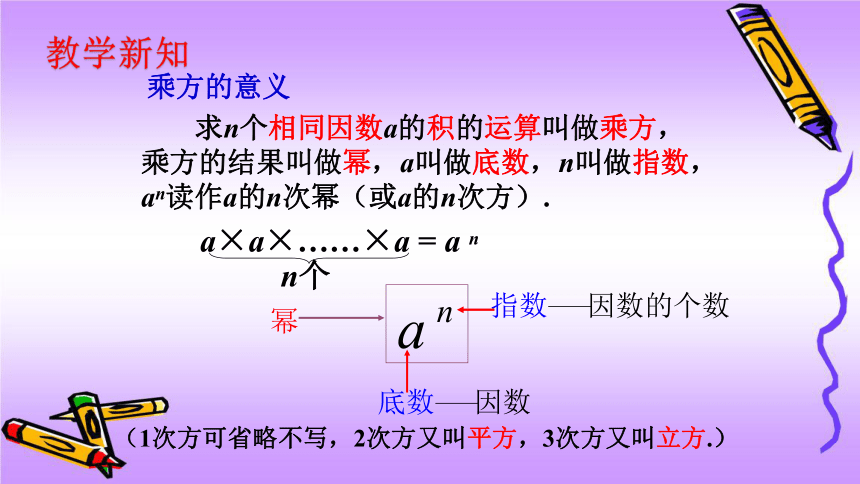
乘方的意义
求n个相同因数a的积的运算叫做乘方,乘方的结果叫做幂,a叫做底数,n叫做指数,an读作a的n次幂(或a的n次方).
(1次方可省略不写,2次方又叫平方,3次方又叫立方.)
教学新知
a×a×……×a = a n
n个
幂
指数
因数的个数
底数
因数
一个数可以看作这个数本身的一次方,例如, ,指数1通常省略不写。
练习
2. 的底数是 ,指数是 ,读作 .
5. 底数是 ,指数是 .
6. X 的底数是 ,指数是 .
1.在 中,15是 数,9是 数,读作 .
3. 中,-6是 数,5是 数,读作 .
4. 的底数是 ,指数是 ,读作 .
(-8)3 与 -83 一样吗? 为什么
研究
(-8)3 是3个 -8 相乘,
-83 是先把3个8相乘,然后取结果的相反数。
把下列乘法式子写成乘方的形式:
1、3×3×3×3×3×3×3
2、(-1)×(-1)×(-1)×(-1)×(-1)×(-1)
3、
把下列乘方写成乘法的形式:
1. 计算:
(1)
(2)
(3)
(4)
(5)
从上面的计算题中,你发现负数的幂的正负有什么规律?当指数是( )数时,负数的幂是( )数;当指数是( )数时,负数的幂是( )数。
奇
偶
正
负
2. 计算:
负数的奇次幂是负数,
负数的偶次幂是正数.
正数的任何次幂都是正数.
0的任何正整数次幂都是0.
乘方的符号法则:
归纳
思考:说说下列各数的意义,它们一样吗
试试你的火眼金睛
计算
达标检测
是___数
是___数
这节课你有哪些收获?
小结
再见
1.5.1 有理数的乘方(1)
教学目标
1.理解有理数乘方的意义,了解幂,乘方,底数,指数等相关概念。
2.掌握有理数乘方的符号法则以及相关性质,能正确进行有理数的乘方的运算。
3.培养学生观察,归纳,分析,思考,概括的能力。
如图,一正方形的边长为3cm,则它的面积为________平方厘米;记作_____,读作_ _ ___,或者是_____。
一正方体的棱长为4cm, 则它的体积为___________立方厘米;记作_____,读作_____,或者是_____。
4×4×4
3×3
3
4
情境导入
3的平方
3的2次方
4的立方
4的3次方
43
4×4×4 记作:
一般的,任意多个相同的有理数相乘,我们如何去简化表示呢?
相同因数的乘法如何简化
3×3记作:
32
43
3是______;
2是______
4是____________,
3是___________
相同的因数
因数的个数
相同的因数
因数的个数
4×4×4×4×4,可以表示为__________,
读作_________,
× × × ,可以表示为__________,
读作 _________,
7×7×7×7×7×7×7,可以表示为__________,
读作_________,1.2×1.2×1.2×1.2×1.2×1.2×1.2,
可以表示为__________,读作_________,
类比上面的形式
(1.2)7
77
4
45
1.2的7次方
7的7次方
的4次方
4的5次方
乘方的意义
求n个相同因数a的积的运算叫做乘方,乘方的结果叫做幂,a叫做底数,n叫做指数,an读作a的n次幂(或a的n次方).
(1次方可省略不写,2次方又叫平方,3次方又叫立方.)
教学新知
a×a×……×a = a n
n个
幂
指数
因数的个数
底数
因数
一个数可以看作这个数本身的一次方,例如, ,指数1通常省略不写。
练习
2. 的底数是 ,指数是 ,读作 .
5. 底数是 ,指数是 .
6. X 的底数是 ,指数是 .
1.在 中,15是 数,9是 数,读作 .
3. 中,-6是 数,5是 数,读作 .
4. 的底数是 ,指数是 ,读作 .
(-8)3 与 -83 一样吗? 为什么
研究
(-8)3 是3个 -8 相乘,
-83 是先把3个8相乘,然后取结果的相反数。
把下列乘法式子写成乘方的形式:
1、3×3×3×3×3×3×3
2、(-1)×(-1)×(-1)×(-1)×(-1)×(-1)
3、
把下列乘方写成乘法的形式:
1. 计算:
(1)
(2)
(3)
(4)
(5)
从上面的计算题中,你发现负数的幂的正负有什么规律?当指数是( )数时,负数的幂是( )数;当指数是( )数时,负数的幂是( )数。
奇
偶
正
负
2. 计算:
负数的奇次幂是负数,
负数的偶次幂是正数.
正数的任何次幂都是正数.
0的任何正整数次幂都是0.
乘方的符号法则:
归纳
思考:说说下列各数的意义,它们一样吗
试试你的火眼金睛
计算
达标检测
是___数
是___数
这节课你有哪些收获?
小结
再见
