13.1.2 第1课时 线段的垂直平分线的性质和判定 人教版八年级数学上册课时作业(含答案)
文档属性
| 名称 | 13.1.2 第1课时 线段的垂直平分线的性质和判定 人教版八年级数学上册课时作业(含答案) | 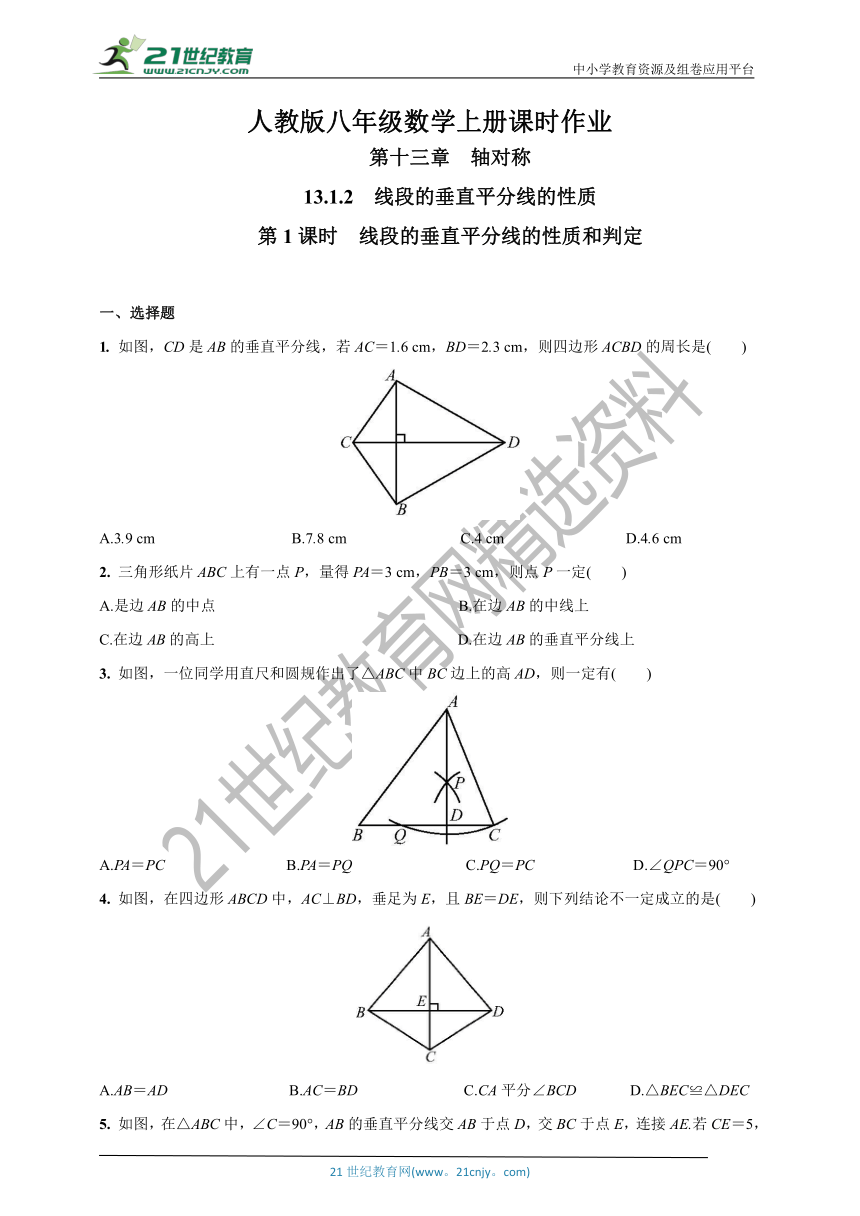 | |
| 格式 | doc | ||
| 文件大小 | 346.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-14 19:21:54 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版八年级数学上册课时作业
第十三章 轴对称
13.1.2 线段的垂直平分线的性质
第1课时 线段的垂直平分线的性质和判定
一、选择题
1. 如图,CD是AB的垂直平分线,若AC=1.6 cm,BD=2.3 cm,则四边形ACBD的周长是( )
A.3.9 cm B.7.8 cm C.4 cm D.4.6 cm
2. 三角形纸片ABC上有一点P,量得PA=3 cm,PB=3 cm,则点P一定( )
A.是边AB的中点 B.在边AB的中线上
C.在边AB的高上 D.在边AB的垂直平分线上
3. 如图,一位同学用直尺和圆规作出了△ABC中BC边上的高AD,则一定有( )
A.PA=PC B.PA=PQ C.PQ=PC D.∠QPC=90°
4. 如图,在四边形ABCD中,AC⊥BD,垂足为E,且BE=DE,则下列结论不一定成立的是( )
A.AB=AD B.AC=BD C.CA平分∠BCD D.△BEC≌△DEC
5. 如图,在△ABC中,∠C=90°,AB的垂直平分线交AB于点D,交BC于点E,连接AE.若CE=5,AC=12,且△ACE的周长为30,则BE的长是( )
A.5 B.10 C.12 D.13
二、填空题
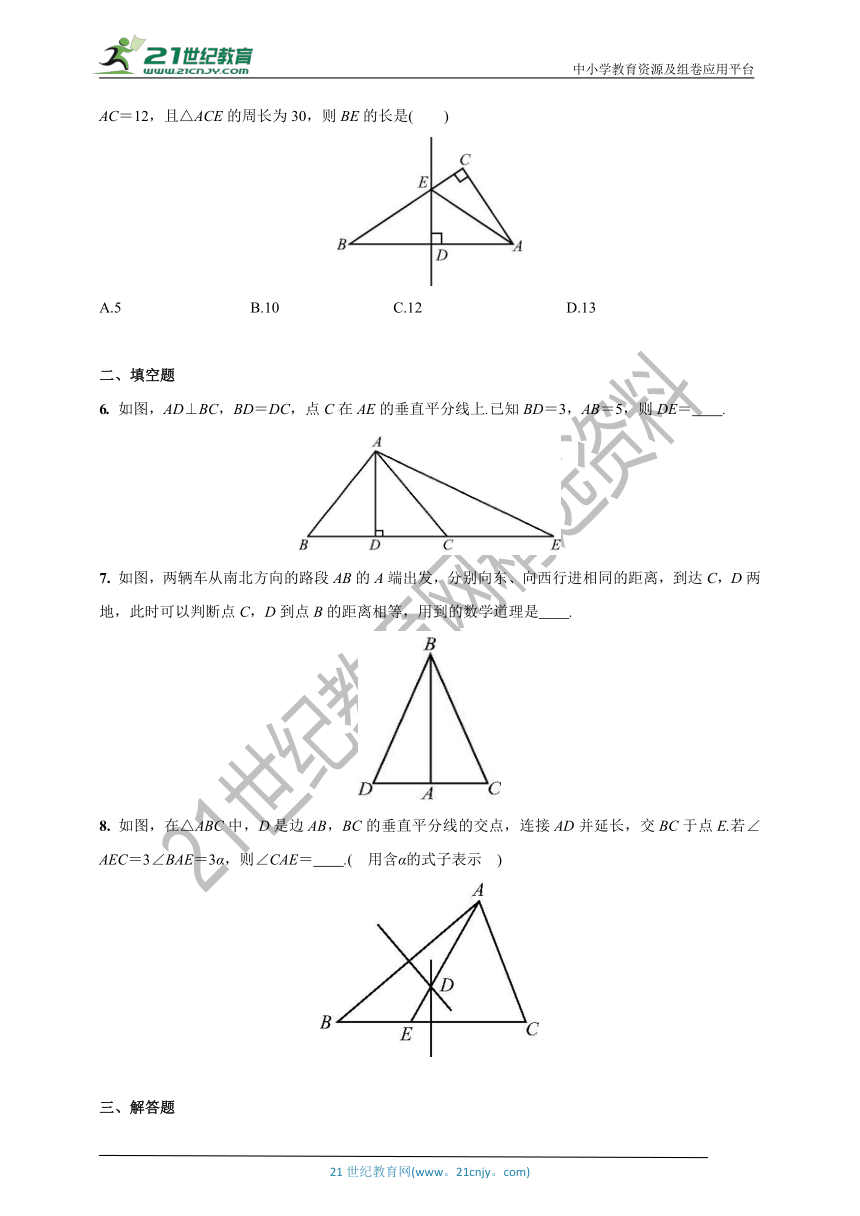
6. 如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上.已知BD=3,AB=5,则DE= .
7. 如图,两辆车从南北方向的路段AB的A端出发,分别向东、向西行进相同的距离,到达C,D两地,此时可以判断点C,D到点B的距离相等,用到的数学道理是 .
8. 如图,在△ABC中,D是边AB,BC的垂直平分线的交点,连接AD并延长,交BC于点E.若∠AEC=3∠BAE=3α,则∠CAE= .( 用含α的式子表示 )
三、解答题
9. 如图,AC=AB,DC=DB,AD与BC相交于点O.求证:AD垂直平分BC.
10. 如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.求证:DE=CE.
11. 如图,已知∠ABC.
(1)求作:∠ABC的平分线BD;(不写作法,保留作图痕迹)
(2)在BD上任取一点P,作直线PQ,使PQ⊥AB.(不写作法,保留作图痕迹)
12. 如图,在△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于点E.
(1)若∠BAC=50°,求∠EDA的度数;
(2)求证:直线AD是线段CE的垂直平分线.
13. 如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O.△ADE的周长为6 cm.
(1)求证:AD=BD,AE=CE;
(2)求BC的长;
(3)分别连接OA,OB,OC,若△OBC的周长为16 cm,求OA的长.
14. 已知在△ABC中,DE垂直平分AB,垂足为D,交直线BC于点E,MN垂直平分AC,垂足为M,交直线BC于点N,连接AE,AN.
图1 图2
(1)如图1,若∠BAC=100°,求∠EAN的大小;
(2)如图2,若∠BAC=70°,求∠EAN的大小;
(3)若∠BAC=α(α≠90°),用含α的式子表示∠EAN的大小.(直接写出结果即可)
参考答案
1. B 2. D 3. C 4. B 5. D
6. 8 7. 垂直平分线上的点到线段两端点的距离相等 8. 90°-2α
9. 证明:∵AB=AC,∴点A在BC的垂直平分线上. ∵DC=DB,∴点D在BC的垂直平分线上,∴AD垂直平分BC.
10. 证明:连接BE,∵DE是AB的垂直平分线,∴BE=AE,∠ABE=∠A=30°. ∵∠ACB=90°,∠A=30°,∴∠ABC=60°,∴∠CBE=∠DBE=30°. ∵DE⊥AB,CE⊥BC,∴DE=CE.
11. 略
12. 解:(1)∵∠BAC=50°,AD平分∠BAC,∴∠EAD=∠BAC=25°. ∵DE⊥AB,∴∠AED=90°,∴∠EDA=90°-25°=65°.
(2)∵DE⊥AB,∴∠AED=90°=∠ACB. 又∵AD平分∠BAC,∴∠DAE=∠DAC. ∵AD=AD,∴△AED≌△ACD,∴AE=AC. ∵AD平分∠BAC,∴AD⊥CE,即直线AD是线段CE的垂直平分线.
13. 解:(1)∵l1是AB边的垂直平分线,l2是AC边的垂直平分线,∴AD=BD,AE=CE.
(2)∵△ADE的周长为6 cm,∴AD+DE+EA=6 cm,∴BD+DE+EC=BC=6 cm.
(3)∵l1是AB边的垂直平分线,l2是AC边的垂直平分线,∴OB=OA,OC=OA. ∵△OBC的周长为16 cm,∴OB+OC+BC=16 cm,∴OB+OC=16-6=10 cm,∴OA=OB=OC=5 cm.
14. 解:(1)∵DE垂直平分AB,∴AE=BE,∴∠BAE=∠B. 同理,得∠CAN=∠C,∴∠EAN=∠BAC-∠BAE-∠CAN=∠BAC-(∠B+∠C)=100°-80°=20°.
(2)∵DE垂直平分AB,∴AE=BE,∴∠BAE=∠B. 同理,得∠CAN=∠C,∴∠EAN=∠BAE+∠CAN-∠BAC=∠B+∠C-∠BAC=110°-70°=40°.
(3)当0°<α<90°时,∠EAN=180°-2α;当90°<α<180°时,∠EAN=2α-180°.
21世纪教育网 www。21cnjy。com精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www。21cnjy。com)
人教版八年级数学上册课时作业
第十三章 轴对称
13.1.2 线段的垂直平分线的性质
第1课时 线段的垂直平分线的性质和判定
一、选择题
1. 如图,CD是AB的垂直平分线,若AC=1.6 cm,BD=2.3 cm,则四边形ACBD的周长是( )
A.3.9 cm B.7.8 cm C.4 cm D.4.6 cm
2. 三角形纸片ABC上有一点P,量得PA=3 cm,PB=3 cm,则点P一定( )
A.是边AB的中点 B.在边AB的中线上
C.在边AB的高上 D.在边AB的垂直平分线上
3. 如图,一位同学用直尺和圆规作出了△ABC中BC边上的高AD,则一定有( )
A.PA=PC B.PA=PQ C.PQ=PC D.∠QPC=90°
4. 如图,在四边形ABCD中,AC⊥BD,垂足为E,且BE=DE,则下列结论不一定成立的是( )
A.AB=AD B.AC=BD C.CA平分∠BCD D.△BEC≌△DEC
5. 如图,在△ABC中,∠C=90°,AB的垂直平分线交AB于点D,交BC于点E,连接AE.若CE=5,AC=12,且△ACE的周长为30,则BE的长是( )
A.5 B.10 C.12 D.13
二、填空题
6. 如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上.已知BD=3,AB=5,则DE= .
7. 如图,两辆车从南北方向的路段AB的A端出发,分别向东、向西行进相同的距离,到达C,D两地,此时可以判断点C,D到点B的距离相等,用到的数学道理是 .
8. 如图,在△ABC中,D是边AB,BC的垂直平分线的交点,连接AD并延长,交BC于点E.若∠AEC=3∠BAE=3α,则∠CAE= .( 用含α的式子表示 )
三、解答题
9. 如图,AC=AB,DC=DB,AD与BC相交于点O.求证:AD垂直平分BC.
10. 如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.求证:DE=CE.
11. 如图,已知∠ABC.
(1)求作:∠ABC的平分线BD;(不写作法,保留作图痕迹)
(2)在BD上任取一点P,作直线PQ,使PQ⊥AB.(不写作法,保留作图痕迹)
12. 如图,在△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于点E.
(1)若∠BAC=50°,求∠EDA的度数;
(2)求证:直线AD是线段CE的垂直平分线.
13. 如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O.△ADE的周长为6 cm.
(1)求证:AD=BD,AE=CE;
(2)求BC的长;
(3)分别连接OA,OB,OC,若△OBC的周长为16 cm,求OA的长.
14. 已知在△ABC中,DE垂直平分AB,垂足为D,交直线BC于点E,MN垂直平分AC,垂足为M,交直线BC于点N,连接AE,AN.
图1 图2
(1)如图1,若∠BAC=100°,求∠EAN的大小;
(2)如图2,若∠BAC=70°,求∠EAN的大小;
(3)若∠BAC=α(α≠90°),用含α的式子表示∠EAN的大小.(直接写出结果即可)
参考答案
1. B 2. D 3. C 4. B 5. D
6. 8 7. 垂直平分线上的点到线段两端点的距离相等 8. 90°-2α
9. 证明:∵AB=AC,∴点A在BC的垂直平分线上. ∵DC=DB,∴点D在BC的垂直平分线上,∴AD垂直平分BC.
10. 证明:连接BE,∵DE是AB的垂直平分线,∴BE=AE,∠ABE=∠A=30°. ∵∠ACB=90°,∠A=30°,∴∠ABC=60°,∴∠CBE=∠DBE=30°. ∵DE⊥AB,CE⊥BC,∴DE=CE.
11. 略
12. 解:(1)∵∠BAC=50°,AD平分∠BAC,∴∠EAD=∠BAC=25°. ∵DE⊥AB,∴∠AED=90°,∴∠EDA=90°-25°=65°.
(2)∵DE⊥AB,∴∠AED=90°=∠ACB. 又∵AD平分∠BAC,∴∠DAE=∠DAC. ∵AD=AD,∴△AED≌△ACD,∴AE=AC. ∵AD平分∠BAC,∴AD⊥CE,即直线AD是线段CE的垂直平分线.
13. 解:(1)∵l1是AB边的垂直平分线,l2是AC边的垂直平分线,∴AD=BD,AE=CE.
(2)∵△ADE的周长为6 cm,∴AD+DE+EA=6 cm,∴BD+DE+EC=BC=6 cm.
(3)∵l1是AB边的垂直平分线,l2是AC边的垂直平分线,∴OB=OA,OC=OA. ∵△OBC的周长为16 cm,∴OB+OC+BC=16 cm,∴OB+OC=16-6=10 cm,∴OA=OB=OC=5 cm.
14. 解:(1)∵DE垂直平分AB,∴AE=BE,∴∠BAE=∠B. 同理,得∠CAN=∠C,∴∠EAN=∠BAC-∠BAE-∠CAN=∠BAC-(∠B+∠C)=100°-80°=20°.
(2)∵DE垂直平分AB,∴AE=BE,∴∠BAE=∠B. 同理,得∠CAN=∠C,∴∠EAN=∠BAE+∠CAN-∠BAC=∠B+∠C-∠BAC=110°-70°=40°.
(3)当0°<α<90°时,∠EAN=180°-2α;当90°<α<180°时,∠EAN=2α-180°.
21世纪教育网 www。21cnjy。com精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www。21cnjy。com)
