4.2万有引力定律的应用 达标作业(word解析版)
文档属性
| 名称 | 4.2万有引力定律的应用 达标作业(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-10-14 06:03:48 | ||
图片预览




文档简介
2021-2022学年鲁科版(2019)必修第二册
4.2万有引力定律的应用 达标作业(解析版)
1.我国发射的探月航天器在接近月球表面的轨道上飞行,其运动视为匀速圆周运动。已知航天器运动的周期为T,引力常量为G,不考虑月球自转的影响,根据上述条件可以计算出( )
A.月球的平均密度 B.月球的质量
C.航天器的质量 D.月球半径
2.为了验证拉住月球使它围绕地球运动的力与拉着苹果下落的力是同一性质的力,同样遵从平方反比定律,牛顿进行了著名的“月地检验”。已知月地之间的距离为 60R(R 为地球半径),月球围绕地球公转的周期为 T,引力常量为 G。则下列说法中正确的是( )
A.由题中信息可以计算出地球的密度为
B.由题中信息可以计算出月球绕地球公转的线速度大小为
C.月球绕地球公转的向心加速度是在地面附近重力加速度的
D.物体在月球轨道上受到的地球引力是其在地面附近受到的地球引力的
3.若在某行星和地球上离各自水平地面的相同高度处,同时由静止释放两质量相同的物体,它们在空中运动的时间之比为,已知该行星的半径约为地球半径的2倍,地球的质量为,由此可知,该行星的质量为( )
A. B. C. D.
4.一个半径是地球半径的倍、质量是地球质量10倍的行星,它表面的重力加速度是地面重力加速度的多少倍( )
A.5倍 B.50倍 C.倍 D.倍
5.地球表面的平均重力加速度为g,地球半径为R,万有引力常量为G,用上述物理量计算出来的地球平均密度是( )
A. B. C. D.
6.2020年12月,如图所示的嫦娥五号着陆器平稳落月,其完成的一系列举世瞩目工作,令全国人民为之振奋。已知月球与地球的密度之比ρ月:ρ地=a,月球与地球的半径之比R月:R地=b,则月球表面与地球表面的重力加速度之比g月:g地等于( )
A. B. C. D.
7.太阳围绕银河系中心的运动可视为匀速圆周运动,其运动速度约为地球绕太阳公转速度的7倍,其轨道半径约为地球绕太阳公转轨道半径的2109倍,为了粗略估算银河系中恒星的数目,可认为银河系的所有恒星的质量都集中在银河中心,且银河系中恒星的平均质量约等于太阳的质量,则银河系中恒星的数目约为( )
A.109 B.1011 C.1013 D.1015
8.已知下列哪组数据,能够估算出地球的质量(万有引力常量G已知) ( )
A.地球绕太阳运行的周期T地及地日中心间的距离r日地
B.月球绕地球运行的周期T月及地日中心间的距离r月地
C.人造地球卫星在地面附近绕行时的速度和运行周期T卫
D.若不考虑地球的自转,已知地球的半径R和地球表面的重力加速度g
9.已知下列某组数据和引力常量G,能计算出地球质量的是( )
A.月球绕地球运行的周期及月球与地球之间的距离
B.地球绕太阳运行的周期及地球与太阳之间的距离
C.人造地球卫星距地面的高度及运行周期
D.若不考虑地球自转,已知地球的半径及重力加速度
10.利用下列哪组数据和引力常量G,可以计算出地球质量( )
A.若不考虑地球自转对重力的影响,已知地球半径和地面重力加速度
B.已知卫星绕地球作匀速圆周运动的轨道半径和周期
C.已知月球绕地球作匀速圆周运动的周期和月球质量
D.已知同步卫星离地面高度和地球自转周期
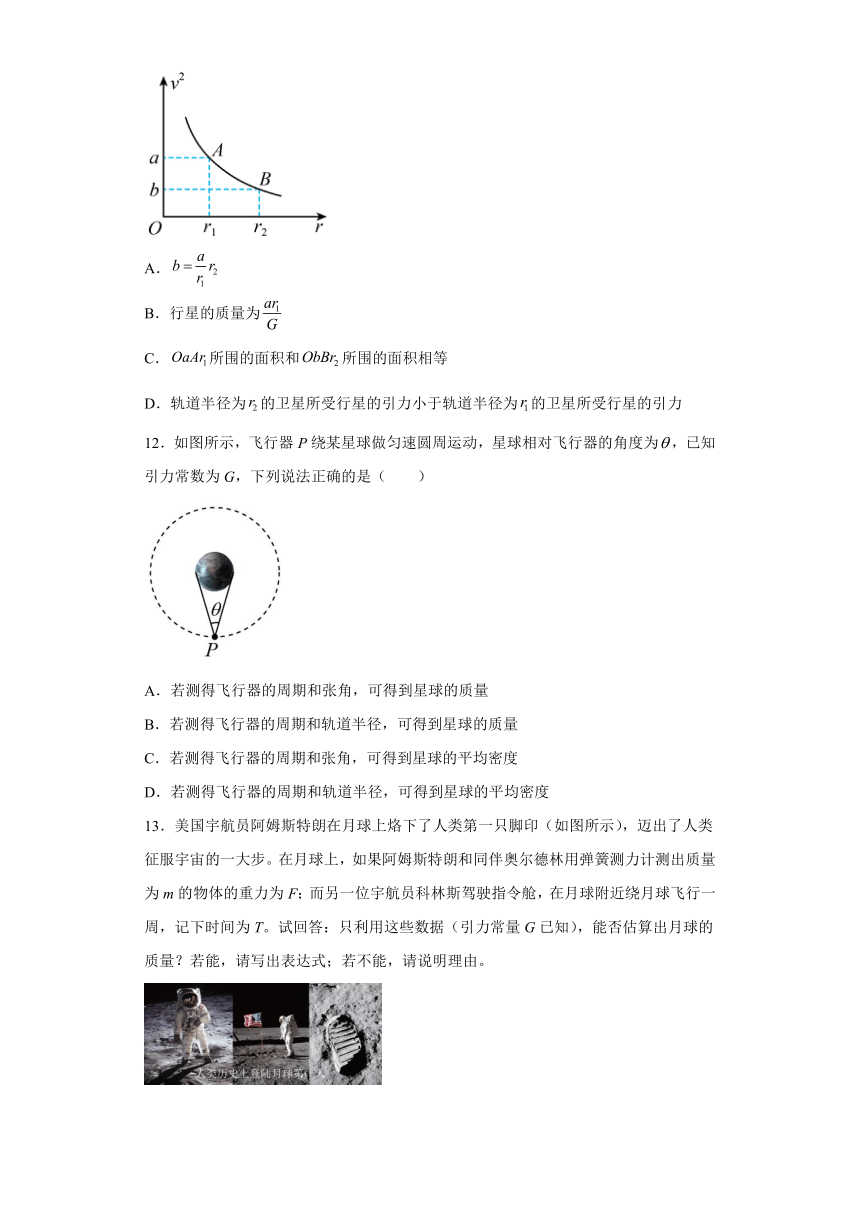
11.某天文爱好者通过测量环绕某行星做匀速圆周运动的若干卫星的线速度v及轨道半径r,得到的图像如图所示,图中a、、已知,b未知.引力常量为G,则下列说法正确的是( )
A.
B.行星的质量为
C.所围的面积和所围的面积相等
D.轨道半径为的卫星所受行星的引力小于轨道半径为的卫星所受行星的引力
12.如图所示,飞行器P绕某星球做匀速圆周运动,星球相对飞行器的角度为,已知引力常数为G,下列说法正确的是( )
A.若测得飞行器的周期和张角,可得到星球的质量
B.若测得飞行器的周期和轨道半径,可得到星球的质量
C.若测得飞行器的周期和张角,可得到星球的平均密度
D.若测得飞行器的周期和轨道半径,可得到星球的平均密度
13.美国宇航员阿姆斯特朗在月球上烙下了人类第一只脚印(如图所示),迈出了人类征服宇宙的一大步。在月球上,如果阿姆斯特朗和同伴奥尔德林用弹簧测力计测出质量为m的物体的重力为F;而另一位宇航员科林斯驾驶指令舱,在月球附近绕月球飞行一周,记下时间为T。试回答:只利用这些数据(引力常量G已知),能否估算出月球的质量?若能,请写出表达式;若不能,请说明理由。
14.如图所示是“月亮女神”、“嫦娥一号”两卫星绕月球做匀速圆周运行时某时刻的图片,用、分别表示“月亮女神”和“嫦娥一号”的周期,用、分别表示月球的半径和“嫦娥一号”的轨道半径。求:
(1)月球的平均密度;
(2)从图示位置开始,经多少时间两卫星第一次相距最远。
15.我国于2018年发射了“嫦娥五号”航天器,航天器在近月轨道上绕月球做匀速圆周运动,经过时间(小于绕行周期),运动的弧长为,航天器与月球中心连线扫过的角度为(弧度),引力常量为,求:
(1)航天器的轨道半径的值;
(2)月球的质量的值。
16.2021年5月15日,我国首次火星探测任务“天问一号”探测器在火星成功着陆,迈出了我国星际探测征程的重要一步。“天问一号”探测器在着陆前,绕火星做匀速圆周运动,其轨道距火星表面的高度为h,周期为T。已知火星半径为R,引力常量为G。求:
(1)火星的质量M;
(2)火星表面的重力加速度g;
参考答案
1.A
【详解】
ABC.对于航天器,由月球对其的万有引力提供航天器做圆周运动的向心力,则
可知,月球的质量为
由于不知道月球的半径,所以月球的质量求不出来。再根据月球的体积为
则月球的平均密度为
所以A正确,BD错误;
C.由题中的已知条件可知,只能求出中心天体的质量,航天器的质量求不出来,所以C错误。
故选A。
2.C
【详解】
A.由引力作为向心力可得
球体的体积公式及密度公式
联立可得地球密度,由题意知,月球的轨道半径r=60R,故A错误;
B.由题中信息可以计算出月球绕地球公转的线速度大小为,B错误;
C.由可知,向心加速度与轨道半径的平方成反比,故满足
C正确;
D.由引力公式可知,物体在月球轨道上受到的地球引力是其在地面附近受到的地球引力的,D错误。
故选C。
3.A
【详解】
根据题意可知,物体在某行星和地球上均做自由落体运动,则有
又因为
所以
则该行星的质量为
BCD错误;A正确。
故选A。
4.A
【详解】
不考虑星球自转,万有引力等于重力
解得
则
故选A。
5.A
【详解】
根据在地球表面万有引力等于重力有
解得
则
故选A。
6.A
【详解】
由公式
且
联立解得
则
g月:g地=
故选A。
7.B
【详解】
地球绕太阳做圆周运动的向心力由太阳对地球的万有引力提供,有
整理得
太阳绕银河系运动也是由万有引力提供向心力,同理可得,银河系的总质量为
由于银河系中恒星的平均质量约等于太阳的质量,则银河系中恒星的数目约为。
故选B。
8.BCD
【详解】
A、根据,知地球的质量在该方程中被约去,不能求出,只能求出太阳的质量.故A错误.
B、根据,知已知月球的周期和月球的轨道半径可以求出地球的质量.故B正确.
C、已知人造地球卫星的周期和线速度,根据v=求出轨道半径,根据,求出地球的质量.故C正确.
D、根据,知地球的质量M=.故D正确.
故选BCD.
9.AD
【详解】
AB.根据
可得
则已知月球绕地球运行的周期及月球与地球之间的距离可求解地球的质量;同理,已知地球绕太阳运行的周期及地球与太阳之间的距离可求解太阳的质量,A正确,B错误;
C.由以上的分析,由可知,已知人造地球卫星距地面的高度及运行周期,因地球的半径未知,则不能求解地球的质量,C错误;
D.若不考虑地球自转,由
可得
则已知地球的半径及重力加速度可求解地球的质量,D正确。
故选AD。
10.AB
【详解】
A.根据
可得
A正确;
B.根据
可得
B正确;
C.根据
可得
由于月球质量两边消去,又无法求出月球绕地球运动的轨道半径,因此无法求出地球质量,C错误;
D.如果只知道同步卫星离地面高度而不知道地球半径,无法求出同步卫星的轨道半径,因此无法求出地球质量,D错误。
故选AB。
11.BC
【详解】
AB.若干卫星绕行星做匀速圆周运动,有
即
对图中A、B两点,有
,
解得
,
故A错误,B正确;
C.所围的面积和所围的面积均为
故C正确;
D.卫星所受行星的引力,由于卫星的质量未知,则引力大小未知,故D错误。
故选BC。
12.BC
【详解】
A.设星球的质量为,半径为,平均密度为,张角为,飞行器的质量为,轨道半径为,周期为,对于飞行器,根据万有引力提供向心力得
由几何关系有
星球的质量
所以测出飞行器的周期和轨道半径,可得到星球的质量,A错误
B.由A选项分析可知测出飞行器的周期和轨道半径,可得到星球的质量,B正确
C.星球的平均密度
所以测得飞行器的周期和张角,可得到星球的平均密度
D.由C选项可知测得飞行器的周期和张角,可得到星球的平均密度,D错误
故选BC。
13.能;
【详解】
设月球的质量为M,半径为R,表面的重力加速度为g,忽略月球自转的影响,根据月球表面物体的重力等于万有引力,有
指令舱在月球附近绕月球的飞行可看作匀速圆周运动,万有引力提供指令舱所需的向心力,有
联立以上两式可得月球的质量为
所以,在已知引力常量G的条件下,能利用题中所给数据估算出月球的质量。
14.(1) ;(2)
【详解】
(1)设月球的质量为, 嫦娥一号的质量为,有
又
联立解得
(2)设经过时间两卫星第一次相距最远,有
解得
15.(1);(2)
【详解】
(1)由几何关系可得
(2)航天器的线速度为
航天器的角速度为
根据万有引力提供向心力有
联立解得
16.(1) ;(2)
【详解】
(1)火星对探测器的万有引力提供向心力,有
可得
(2)由
可得
4.2万有引力定律的应用 达标作业(解析版)
1.我国发射的探月航天器在接近月球表面的轨道上飞行,其运动视为匀速圆周运动。已知航天器运动的周期为T,引力常量为G,不考虑月球自转的影响,根据上述条件可以计算出( )
A.月球的平均密度 B.月球的质量
C.航天器的质量 D.月球半径
2.为了验证拉住月球使它围绕地球运动的力与拉着苹果下落的力是同一性质的力,同样遵从平方反比定律,牛顿进行了著名的“月地检验”。已知月地之间的距离为 60R(R 为地球半径),月球围绕地球公转的周期为 T,引力常量为 G。则下列说法中正确的是( )
A.由题中信息可以计算出地球的密度为
B.由题中信息可以计算出月球绕地球公转的线速度大小为
C.月球绕地球公转的向心加速度是在地面附近重力加速度的
D.物体在月球轨道上受到的地球引力是其在地面附近受到的地球引力的
3.若在某行星和地球上离各自水平地面的相同高度处,同时由静止释放两质量相同的物体,它们在空中运动的时间之比为,已知该行星的半径约为地球半径的2倍,地球的质量为,由此可知,该行星的质量为( )
A. B. C. D.
4.一个半径是地球半径的倍、质量是地球质量10倍的行星,它表面的重力加速度是地面重力加速度的多少倍( )
A.5倍 B.50倍 C.倍 D.倍
5.地球表面的平均重力加速度为g,地球半径为R,万有引力常量为G,用上述物理量计算出来的地球平均密度是( )
A. B. C. D.
6.2020年12月,如图所示的嫦娥五号着陆器平稳落月,其完成的一系列举世瞩目工作,令全国人民为之振奋。已知月球与地球的密度之比ρ月:ρ地=a,月球与地球的半径之比R月:R地=b,则月球表面与地球表面的重力加速度之比g月:g地等于( )
A. B. C. D.
7.太阳围绕银河系中心的运动可视为匀速圆周运动,其运动速度约为地球绕太阳公转速度的7倍,其轨道半径约为地球绕太阳公转轨道半径的2109倍,为了粗略估算银河系中恒星的数目,可认为银河系的所有恒星的质量都集中在银河中心,且银河系中恒星的平均质量约等于太阳的质量,则银河系中恒星的数目约为( )
A.109 B.1011 C.1013 D.1015
8.已知下列哪组数据,能够估算出地球的质量(万有引力常量G已知) ( )
A.地球绕太阳运行的周期T地及地日中心间的距离r日地
B.月球绕地球运行的周期T月及地日中心间的距离r月地
C.人造地球卫星在地面附近绕行时的速度和运行周期T卫
D.若不考虑地球的自转,已知地球的半径R和地球表面的重力加速度g
9.已知下列某组数据和引力常量G,能计算出地球质量的是( )
A.月球绕地球运行的周期及月球与地球之间的距离
B.地球绕太阳运行的周期及地球与太阳之间的距离
C.人造地球卫星距地面的高度及运行周期
D.若不考虑地球自转,已知地球的半径及重力加速度
10.利用下列哪组数据和引力常量G,可以计算出地球质量( )
A.若不考虑地球自转对重力的影响,已知地球半径和地面重力加速度
B.已知卫星绕地球作匀速圆周运动的轨道半径和周期
C.已知月球绕地球作匀速圆周运动的周期和月球质量
D.已知同步卫星离地面高度和地球自转周期
11.某天文爱好者通过测量环绕某行星做匀速圆周运动的若干卫星的线速度v及轨道半径r,得到的图像如图所示,图中a、、已知,b未知.引力常量为G,则下列说法正确的是( )
A.
B.行星的质量为
C.所围的面积和所围的面积相等
D.轨道半径为的卫星所受行星的引力小于轨道半径为的卫星所受行星的引力
12.如图所示,飞行器P绕某星球做匀速圆周运动,星球相对飞行器的角度为,已知引力常数为G,下列说法正确的是( )
A.若测得飞行器的周期和张角,可得到星球的质量
B.若测得飞行器的周期和轨道半径,可得到星球的质量
C.若测得飞行器的周期和张角,可得到星球的平均密度
D.若测得飞行器的周期和轨道半径,可得到星球的平均密度
13.美国宇航员阿姆斯特朗在月球上烙下了人类第一只脚印(如图所示),迈出了人类征服宇宙的一大步。在月球上,如果阿姆斯特朗和同伴奥尔德林用弹簧测力计测出质量为m的物体的重力为F;而另一位宇航员科林斯驾驶指令舱,在月球附近绕月球飞行一周,记下时间为T。试回答:只利用这些数据(引力常量G已知),能否估算出月球的质量?若能,请写出表达式;若不能,请说明理由。
14.如图所示是“月亮女神”、“嫦娥一号”两卫星绕月球做匀速圆周运行时某时刻的图片,用、分别表示“月亮女神”和“嫦娥一号”的周期,用、分别表示月球的半径和“嫦娥一号”的轨道半径。求:
(1)月球的平均密度;
(2)从图示位置开始,经多少时间两卫星第一次相距最远。
15.我国于2018年发射了“嫦娥五号”航天器,航天器在近月轨道上绕月球做匀速圆周运动,经过时间(小于绕行周期),运动的弧长为,航天器与月球中心连线扫过的角度为(弧度),引力常量为,求:
(1)航天器的轨道半径的值;
(2)月球的质量的值。
16.2021年5月15日,我国首次火星探测任务“天问一号”探测器在火星成功着陆,迈出了我国星际探测征程的重要一步。“天问一号”探测器在着陆前,绕火星做匀速圆周运动,其轨道距火星表面的高度为h,周期为T。已知火星半径为R,引力常量为G。求:
(1)火星的质量M;
(2)火星表面的重力加速度g;
参考答案
1.A
【详解】
ABC.对于航天器,由月球对其的万有引力提供航天器做圆周运动的向心力,则
可知,月球的质量为
由于不知道月球的半径,所以月球的质量求不出来。再根据月球的体积为
则月球的平均密度为
所以A正确,BD错误;
C.由题中的已知条件可知,只能求出中心天体的质量,航天器的质量求不出来,所以C错误。
故选A。
2.C
【详解】
A.由引力作为向心力可得
球体的体积公式及密度公式
联立可得地球密度,由题意知,月球的轨道半径r=60R,故A错误;
B.由题中信息可以计算出月球绕地球公转的线速度大小为,B错误;
C.由可知,向心加速度与轨道半径的平方成反比,故满足
C正确;
D.由引力公式可知,物体在月球轨道上受到的地球引力是其在地面附近受到的地球引力的,D错误。
故选C。
3.A
【详解】
根据题意可知,物体在某行星和地球上均做自由落体运动,则有
又因为
所以
则该行星的质量为
BCD错误;A正确。
故选A。
4.A
【详解】
不考虑星球自转,万有引力等于重力
解得
则
故选A。
5.A
【详解】
根据在地球表面万有引力等于重力有
解得
则
故选A。
6.A
【详解】
由公式
且
联立解得
则
g月:g地=
故选A。
7.B
【详解】
地球绕太阳做圆周运动的向心力由太阳对地球的万有引力提供,有
整理得
太阳绕银河系运动也是由万有引力提供向心力,同理可得,银河系的总质量为
由于银河系中恒星的平均质量约等于太阳的质量,则银河系中恒星的数目约为。
故选B。
8.BCD
【详解】
A、根据,知地球的质量在该方程中被约去,不能求出,只能求出太阳的质量.故A错误.
B、根据,知已知月球的周期和月球的轨道半径可以求出地球的质量.故B正确.
C、已知人造地球卫星的周期和线速度,根据v=求出轨道半径,根据,求出地球的质量.故C正确.
D、根据,知地球的质量M=.故D正确.
故选BCD.
9.AD
【详解】
AB.根据
可得
则已知月球绕地球运行的周期及月球与地球之间的距离可求解地球的质量;同理,已知地球绕太阳运行的周期及地球与太阳之间的距离可求解太阳的质量,A正确,B错误;
C.由以上的分析,由可知,已知人造地球卫星距地面的高度及运行周期,因地球的半径未知,则不能求解地球的质量,C错误;
D.若不考虑地球自转,由
可得
则已知地球的半径及重力加速度可求解地球的质量,D正确。
故选AD。
10.AB
【详解】
A.根据
可得
A正确;
B.根据
可得
B正确;
C.根据
可得
由于月球质量两边消去,又无法求出月球绕地球运动的轨道半径,因此无法求出地球质量,C错误;
D.如果只知道同步卫星离地面高度而不知道地球半径,无法求出同步卫星的轨道半径,因此无法求出地球质量,D错误。
故选AB。
11.BC
【详解】
AB.若干卫星绕行星做匀速圆周运动,有
即
对图中A、B两点,有
,
解得
,
故A错误,B正确;
C.所围的面积和所围的面积均为
故C正确;
D.卫星所受行星的引力,由于卫星的质量未知,则引力大小未知,故D错误。
故选BC。
12.BC
【详解】
A.设星球的质量为,半径为,平均密度为,张角为,飞行器的质量为,轨道半径为,周期为,对于飞行器,根据万有引力提供向心力得
由几何关系有
星球的质量
所以测出飞行器的周期和轨道半径,可得到星球的质量,A错误
B.由A选项分析可知测出飞行器的周期和轨道半径,可得到星球的质量,B正确
C.星球的平均密度
所以测得飞行器的周期和张角,可得到星球的平均密度
D.由C选项可知测得飞行器的周期和张角,可得到星球的平均密度,D错误
故选BC。
13.能;
【详解】
设月球的质量为M,半径为R,表面的重力加速度为g,忽略月球自转的影响,根据月球表面物体的重力等于万有引力,有
指令舱在月球附近绕月球的飞行可看作匀速圆周运动,万有引力提供指令舱所需的向心力,有
联立以上两式可得月球的质量为
所以,在已知引力常量G的条件下,能利用题中所给数据估算出月球的质量。
14.(1) ;(2)
【详解】
(1)设月球的质量为, 嫦娥一号的质量为,有
又
联立解得
(2)设经过时间两卫星第一次相距最远,有
解得
15.(1);(2)
【详解】
(1)由几何关系可得
(2)航天器的线速度为
航天器的角速度为
根据万有引力提供向心力有
联立解得
16.(1) ;(2)
【详解】
(1)火星对探测器的万有引力提供向心力,有
可得
(2)由
可得
同课章节目录
- 第1章 功和机械能
- 导入 神奇之能
- 第1节 机械功
- 第2节 功率
- 第3节 动能和动能定理
- 第4节 势能及其改变
- 第5节 科学验证:机械能守恒定律
- 第2章 抛体运动
- 导入 更准、更远
- 第1节 运动的合成与分解
- 第2节 平抛运动
- 第3节 科学探究:平抛运动的特点
- 第4节 生活中的抛体运动
- 第3章 圆周运动
- 导入 生活中的圆周运动
- 第1节 匀速圆周运动快慢的描述
- 第2节 科学探究:向心力
- 第3节 离心现象
- 第4章 万有引力定律及航天
- 导入 从嫦娥奔月到“阿波罗”上天
- 第2节 万有引力定律的应用
- 第3节 人类对太空的不懈探索
- 第5章 科学进步无止境
- 导入 再次跨越时空的对话
- 第1节 初识相对论
- 第2节 相对论中的神奇时空
- 第3节 探索宇宙的奥秘
