第一章 有理数1.1正负数-1.2.4绝对值学案(无答案)
文档属性
| 名称 | 第一章 有理数1.1正负数-1.2.4绝对值学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 508.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-14 16:22:44 | ||
图片预览




文档简介
第一章 有理数
1.1 正数和负数
学习目标:
1.了解负数的来源.
2.理解正数、零、负数表示的意义.
3.会用正、负数表示具有相反意义的量.
知识总结:
1.正数与负数
(1)正数:大于 的数.
(2)负数:在正数前加上符号“”(负)的数.
(3)特例:0既不是_____,也不是_____.
2.用正负数表示相反意义的量
增长和减少、高出和低于、收入和支出、盈利和亏损等都是具有_____意义的量,通常增长、高出、收入、盈利等我们用___数表示,而减少、低于、支出、亏损等我们用___数表示.
考点一 正数与负数
例1 判断下列各数哪些是正数,哪些是负数?
+2013,-3.2, ,10.72,-9,+1,-45.6,0, ,-2.14,
课堂训练
1.在1,-2,-5.5,0,,,3.14中,负数的个数为( )
A.3 B.4 C.5 D.6
【互动探究】上题中,正数有几个?里面有没有既不是正数也不是负数的数?
2.下列结论中,正确的是( )
A.0是正数 B.0是最小的正数
C.0是负数 D.现在学的数可分为正数、负数和0三类
考点二 用正负数表示具有相反意义的量
例1 某日林芳在一条东西方向的公路上跑步,她从A地出发,如果向西跑100m记作-100m,那么她折回来又继续跑了110m是什么意思?这时她停下来休息,此时她在A地的什么方向?距A地多远?林芳共跑了多少米?
例2 某中学对初一新生进行立定跳远测试,规定男生能跳170cm及以上为达标,超过170cm的数用正数表示,不足170cm的数用负数表示,第一组10名男生成绩(单位:cm)如下:
求第一组有百分之几的学生达标?
课堂训练
1.李白出生于公元701年,我们记作+701,那么秦始皇出生于公元前259年,可记作( )
A.259 B.-259 C.-957 D.445
2 .每袋大米以50kg为标准,其中超过标准的千克数记为正数,不足的千克数记为负数,则图中第3袋大米的实际重量是___ kg.
3. 某机器零件的设计图纸上写有“”,根据图纸上的信息,判断该零件长度(L)尺寸合格的是( )
A.9.68mm B.9.97mm C.10.1mm D.10.01mm
4. 某公交车原坐18人,经过3人站点时上下车情况如下(上车为正,下车为负):
(+3, 8),(+5, 7),(+4, 2),则现在车上人数还有___.
5. 刘明上周五在股市以收盘价(收市时的价格)每股25元买进某公司股票2000股,在接下来的一周交易日内,小王记下该股票每日收盘价格相比前一天的涨跌情况:(单位:元)
星期 一 二 三 四 五
每股涨跌 +2 -0.5 +1.5 -1.8 +0.8
根据上表回答问题:
(1)星期二收盘时,该股票每股多少元?
(2)本周内该股票收盘时的最高价,最低价分别是多少?
(3)已知买入股票与卖出股票均需支付成交金额的千分之三的交易费.若小王在本周五以收盘价将全部股票卖出,他的收益情况如何?
6.“十一”黄金周,坚胜家电城大力促销,收银情况一直看好.下表为当天与前一天的营业额的涨跌情况.已知9月30日的营业额为26万元.
10月1日 2日 3日 4日 5日 6日 7日
4 3 2 0
(1)黄金周内收入最低的哪一天?直接回答,不必写过程.
(2)黄金周内平均每天的营业额是多少?
拓展探究
7 .有一列数如下:1,0,1,0,0,1,0,0,0,1,0,0,0,0,1,…,则第9个1在这列数中是第______个数。
8.如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动,它从A处出发去看望B,C,D格点处的其他甲虫,规定:向上向右走均为正,向下向左走均为负,如果从A到B记为A→B{1,4},从B到A记为B→A{ 1, 4},其中第一个数表示左右方向移动,第二个数表示上下方向移动。
(1)图中A→C{___,___},C→D{___,___};
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
第一章 有理数
1.2 有理数
学习目标:
1.理解有理数的含义.
2.能够把给出的有理数正确分类.
3.了解0在有理数分类中的作用.
知识总结:
1.有理数:在数学中,我们将_____和_____统称为有理数.
2.有理数的分类
注:①小学学过的π是正数,但不是有理数;
②"四非":即非负数,非负整数,非正数,非正整数(不要丢掉“0”);
③"0"既不是正数也不是负数;
考点一 有理数的有关概念
1.下列说法正确的是( )
A.整数就是正整数和负整数 B.非负整数就是正整数
C.有理数中不是负数就是正数 D.零是自然数,但不是正整数
2.下列说法错误的是( )
A.负整数和负分数统称为负有理数 B.正整数,0,负整数统称为整数
C.正有理数与负有理数组成全体有理数 D.3.14是小数,也是分数
3.有理数-8,20, ,0,-5,+13, ,-7.2中,非负有理数与分数共有( )
A.4个 B.5个 C.6个 D.7个
考点二 有理数的分类
例1 把下列各数填入相应的大括号里:
-5,10,-4.5, ,-2.15,0.01,+66, ,15%, ,,2014,-16.
正整数集合:{ …};
负整数集合:{ …};
负分数集合:{ …};
正分数集合:{ …};
负有理数集合:{ …};
有理数集合:{ …}.
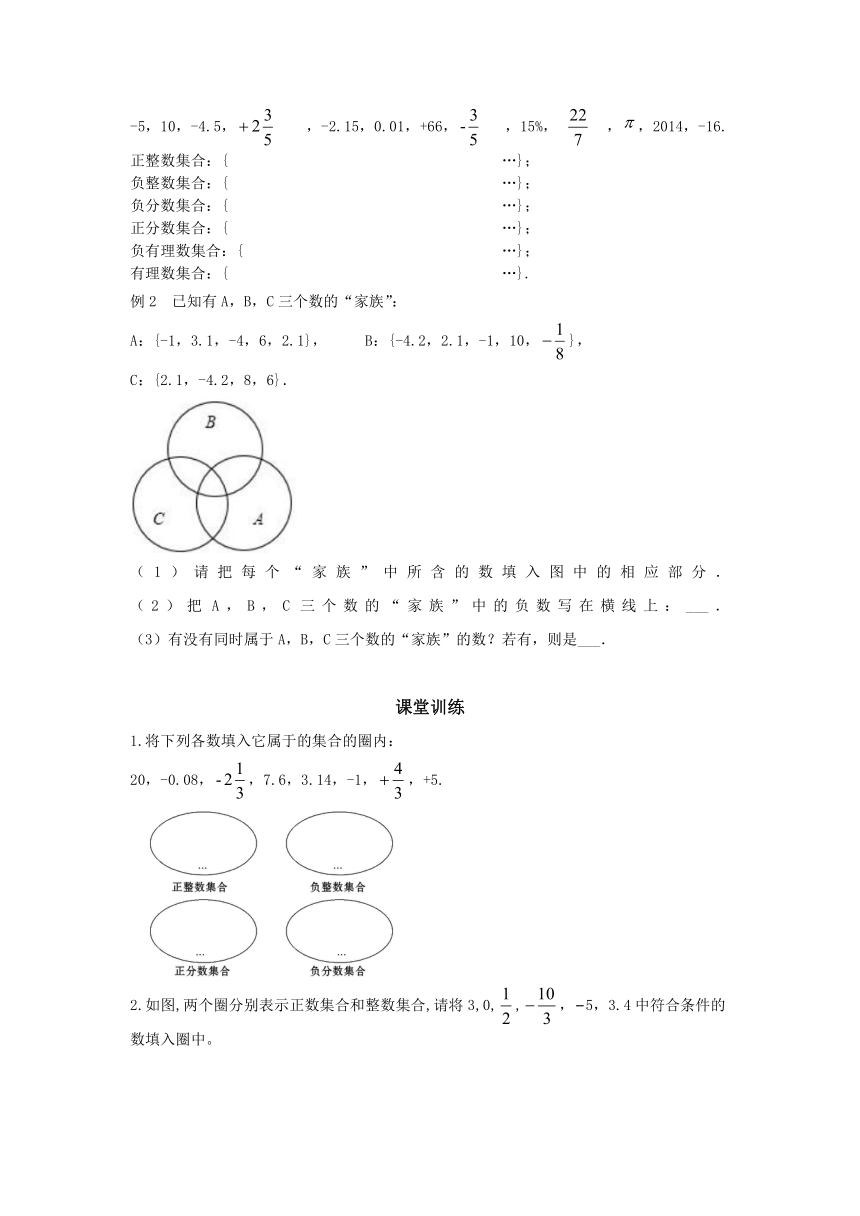
例2 已知有A,B,C三个数的“家族”:
A:{-1,3.1,-4,6,2.1}, B:{-4.2,2.1,-1,10,},
C:{2.1,-4.2,8,6}.
(1)请把每个“家族”中所含的数填入图中的相应部分.
(2)把A,B,C三个数的“家族”中的负数写在横线上:___.
(3)有没有同时属于A,B,C三个数的“家族”的数?若有,则是___.
课堂训练
1.将下列各数填入它属于的集合的圈内:
20,-0.08,,7.6,3.14,-1,,+5.
2.如图,两个圈分别表示正数集合和整数集合,请将3,0,,, 5,3.4中符合条件的数填入圈中。
3.如图所示,今有A,B,C三个数集,每个数集中所包含的数都写在下面的大括号内,请把这些数填入对应的三个圈内.A={3,2,0,4},B={5,6,-5,0,2},C={-5,0,4,-2}.
拓展探究
1.将一串有理数按下列规律排列,回答下列问题.
(1)在A处的数是正数还是负数?
(2)负数排在A,B,C,D中的什么位置?
(3)第2019个数是正数还是负数?排在对应于A,B,C,D中的什么位置?
2.在小学我们学习了偶数0,2,4,6,8,…,以及奇数1,3,5,7,9,…,现在我们学过了负数,也知道了负偶数与负奇数,负偶数 2, 4, 6, 8,…,负奇数 1, 3, 5, 7,…,下面我们将这些负偶数与负奇数排列如图所示:
在上述的这些数中,观察它们的规律,并求 101在哪一列。
第一章 有理数
1.2 数轴
1.定义:规定了原点、正方向和单位长度的直线叫做数轴.
注:①数轴的三要素:原点、正方向、单位长度;
②有理数都能在数轴表示出来,但数轴上的点不都代表有理数,比如π.
例1 四位同学画数轴如下图所示,你认为正确的是( ).
B.
C. D.
例2 点A表示数轴上的一个点,将点A向右移动10个单位,再向左移动6个单位,终点恰好是原点,则点A表示的数是___.
例3 数轴上表示整数的点称为整点,某数轴的单位长度是1厘米,若在这个数轴上随意画出一条长为2020厘米的线段AB,则线段AB盖住的整点个数是()
A.2018或2019 B.2019或2020 C.2020或2021 D.2021或2022
例4 操作探究:已知在纸面上有一数轴(如图所示),
操作一:
(1)折叠纸面,使表示的1点与 1表示的点重合,则 3表示的点与___表示的点重合;
操作二:
(2)折叠纸面,使 1表示的点与3表示的点重合,回答以下问题:
①5表示的点与数___表示的点重合;
②若数轴上A. B两点之间距离为11,(A在B的左侧),且A. B两点经折叠后重合,求A. B两点表示的数是多少。
课堂训练
1.图中所画的数轴,正确的是( )
A. B.
C. D.
2.数轴上点A表示 2,从A出发,沿数轴移动4个单位长度到达点B,则点B表示的数是______.
3.数轴上一点A,一只蚂蚁从A出发爬了4个单位长度到了点3,则点A所表示的数是______.
4.已知点A在数轴上表示的数是-2,点B到原点的距离等于3,则A、B两点间的距离是 。
5.有理数m、n在数轴上的位置如图所示,下列判断正确的是( )
A. m<0 B. m>1 C. n> 1 D. n< 1
6.如图,数轴上有M,N,P,Q四个点,其中点P所表示的数为a,则数 3a所对应的点可能是( )
A. M B. N C. P D. Q
7.如图,在数轴上,点A表示的数为 1,点B表示的数为4,C是点B关于点A的对称点,则点C表示的数为____。
8.已知A,B,C是数轴上的三个点,且C在B的右侧。点A,B表示的数分别是1,3,如图所示。若BC=2AB,则点C表示的数是___.
9.如图,将一刻度尺放在数轴上(数轴的单位长度是1cm),刻度尺上“1cm”和“9cm”分别对应数轴上的 3和x,那么x的值为___.
10.在数轴上,老师不小心把一滴墨水滴在画好的数轴上,如图所示,试根据图中标出的数值判断被墨水盖住的整数有______个.
11.在下面给出的数轴中A表示1,B表示 2.5,回答下面的问题:
(1)A、B之间的距离是___.
(2)观察数轴,与点A的距离为5的点表示的数是:___;
(3)若将数轴折叠,使A点与 2表示的点重合,则B与数___表示的点重合.
(4)若数轴上M、N两点之间的距离为2016(M在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是:M:___,N:___.
12.小敏家、学校、邮局、图书馆坐落在一条东西走向的大街上,依次记为A,B,C,D,学校位于小敏家西150米,邮局位于小敏家东100米,图书馆位于小敏家西400米。
(1)用数轴表示A,B,C,D的位置;
(2)一天小敏从家里先去邮局寄信后,再以每分钟50米的速度往图书馆方向走了约8分钟。试问这时小敏约在什么位置 距图书馆和学校各约多少米
拓展探究
13.如图,圆的周长为4个单位长,数轴每个数字之间的距离为1个单位,在圆的四等分点处分别标上0,1,2,3,先让圆周上表示数字0的点与数轴上表示 1的点重合。再将数轴按逆时针方向环绕在该圆上(如圆周上表示的数字3的点与数轴上表示 2的点重合……),则该数轴上表示 2019的点与圆周上重合的点表示的数字是( )
A. 0 B. 1 C. 2 D. 3
14.等边三角形(三条边都相等的三角形是等边三角形)纸板ABC在数轴上的位置如图所示,点A,B对应的数分别为0和 1,若△ABC绕着顶点顺时针方向在数轴上连续翻转,翻转第1次后,点C所对应的数为1,则翻转2020次后,点C所对应的数是( )
A.2017 B.2018 C.2019 D.2020
第一章 有理数
1.2相反数
1.相反数的定义及其性质
(1)定义:只有符号不同的两个数.特别地,0的相反数是0.一般地,a和-a互为相反数.
(2)求法:在任意一个数的前面添上负号,新的数就表示原数的相反数.
注:①若a与b互为相反数,则a+b=0,反之也成立;
②在数轴上,表示互为相反数的两个点,位于原点的两侧,且到原点的距离相等
2.多重符号的化简
若一个正数前有偶数个负号,结果为正;若一个正数有奇数个负号,结果为负.
例1 下列说法中,正确的是( )
A.因为相反数是成对出现的,所以0没有相反数
B.数轴上原点两旁的两点表示的数是互为相反数
C.符号不同的两个数是互为相反数
D.正数的相反数是负数,负数的相反数是正数
例2 给出下列各组数:①-1与+(-1);②+(+1)与-1;③-(+4)与-(-4);④-(+1.7)与+(-1.7);⑤-[+(-8)]与-[-(+8)]。其中互为相反数的有__________________(填写序号).
例3 若-{-[+(-a)]}与-(+4)互为相反数,则-[+(-a)]=______.
例4 如图,数轴上一动点A向左移动2个单位长度到达点B,再向右移动5个单位长度到达点C.若点C表示的数为1,则与点A表示的数互为相反数的是______.
课堂训练
下列说法中正确的有( )
①π的相反数是-3.14;②符号相反的数互为相反数;③一个数的相反数可能与它相等;④-(-3.8)的相反数是-3.8;⑤正数与负数互为相反数.
2.给出下列各数:+(-10),-(+15),-(-7),-[+(-a)],-[-(-20)].其中相反数一定为负数的有______个.
3.若-a=-(-4),则+[-(-a)]=______.
4.若-[+(-5)]=a,则-a的相反数是______.
5.如果a的相反数是最大的负整数,b的相反数是最小的正整数,则a+b=______.
6.数轴上A和B所表示的点互为相反数,且两个点之间的距离为14,则A和B这两个数分别为______.
7.数轴上点A表示 3,B和C两点所表示的数互为相反数,且点B到点A的距离为3,则点C所表示的数应是______.
8.如图,数轴的单位长度为1,回答下列问题:
(1)如果点A和C表示的数互为相反数,那么点D表示的数是多少
(2)如果点C和E表示的数互为相反数,那么点B和D表示的数是多少
9.已知表示数a的点在数轴上的位置如图所示。
(1)若数a与其相反数相距20个单位长度,则a表示的数是多少
(2)在(1)的条件下,若数b表示的数与数a的相反数表示的点相距5个单位长度,求b表示的数是多少
第一章 有理数
1.2.4绝对值
一.绝对值
(1)定义:数轴上表示数a的点与原点的距离叫做数a的绝对值.
(2)记法:数a的绝对值记作|a|.
(3)代数结论:正数的绝对值是它本身;负数的绝对值是它的相反数;0的绝对值是0.也即
(4)注意:①对任何数a,都有.②若|a|=|b|,则a=b或a=-b.③若|a|+|b|=0,则a=b=0.
二.比较大小
数轴法:数轴上右边的数大于左边的数.
代数法:①正数>0>负数,②两个负数比大小,绝对值大的反而小.
考点一 绝对值
例1 下列说法中正确的个数有( ).
①互为相反数的两个数的绝对值相等;②绝对值等于本身的数只有正数;③不相等的两个数的绝对值不相等;④绝对值相等的两个数一定相等.
A.1个 B.2个 C.3个 D.4个
例2 已知a=-8,|a|=|b|,求b的值.
例3 已知|x 4|+|2y+2|=0,求2x |y|的值。
例4 下列说法正确的是( )
A.如果|a|=|b|,那么a=b B.如果|a|>|b|,那么a>b
C.如果a>|b|,那么a>b D.如果a>b,那么|a|>|b|
例5 阅读下列材料:我们知通|x|的几何意义是数轴上数x的对应点与原点之间的距离,即|x|=|x-0|,也可以说,|x|表示数轴上数x与数0对应点之间的路离。这个结论可以推广为表示数轴上数与数对应点之间的距离.
举例1:已知|x|=2,求x的值.
解:在数轴上与原点距离为2的点表示的数为-2和2,
所以x的值为-2或2.
举例2:已知,求x的值.
解:在数轴上与1对应的点的距离为2的点表示的数为3和-1.
所以x的值为3或-1.
仿照材料中的解法,求下列各式中x的值.
(1)|x|=3; (2)|x+2|=4; (3)|x-3|=|x+1|.
课堂训练
1.下列各组数中,互为相反数的是( )
A. 3与 B.| 3|与3 C.与 D.与
2. 在-2,|-2|,-|-2|,-(-2),-(+2),-|+2|中,负数的个数是_____。
3.若-|-a|=-|-4|,则a= .
4.绝对值大于2且小于5的整数是____.
5.若a,b互为相反数, c,d互为倒数,x的绝对值是1,求的值。
8.下列说法正确的是( )
A. a的绝对值是a B.若|x|= x,则x是负数 C.a的绝对值是a D.若m= n,则|m|=|n|
9.下列判断正确的是( )
A.若|a|=|-b|,则a=b B.若|a|=|b|,则a=-b
C.若a=b,则|a|=|b| D.若a=-b,则|a|=-|b|
10.如图,实数 3,x,3,y在数轴上的对应点分别为M、N、P、Q,这四个数中绝对值最大的数对应的点是( )
A. 点M B. 点N C. 点P D. 点Q
11.如图,四个有理数在数轴上的对应点M,P,N,Q,若点M,P表示的有理数互为相反数,则图中表示绝对值最大的数的点是( )
A.点M B.点N C.点P D.点Q
12.如图,数轴上的A. B. C三点所表示的数分别为a、b、c,其中AB=BC,如果|a|>|b|>|c|,那么该数轴的原点O的位置应该在( )
A.点A的左边 B.点A与点B之间 C.点B与点C之间 D.点C的右边
13.如图,若数轴上a的绝对值是b的绝对值的3倍,则数轴的原点在点______或点______.(填“A”、“B”“C”或“D”)
14.回答下列问题
(1)数轴上表示2和5的两点之间的距离是_____,数轴上表示-2和-5的两点之间的距离是_____,数轴上表示1和-3的两点之间的距离是_____;
(2)数轴上表示x和-1的两点A和B之间的距离|AB|=2,那么x为_____.
考点二 比较大小
例1 在三个有理数a、b、c中,a、b都是负数,c是正数,且|b|>|a|>|c|.
(1)在数轴上表示出a,b,c三个数的大致位置;
(2)比较a,b,c的大小.
课堂训练
1.比较下列各对数的大小:
(1)-(-3)和|-2|; (2) -(-4)和-|-4|;
(3) -|-5|和+(-6); (4) -|+1|和-(+3)
2.若a,b两数在数轴上位置如图所示,将a、b、-a、-b用“<”连接,其中正确的是( )
A.a<-a<b<-b B.-b<a<-a<b C.-a<b<-b<a D.-b<a<b<-a
3.若a,b为有理数,a>0,b<0,且|a|<|b|,则a,b,-a,|b|的大小关系是____
4.己知a>0,b<0,a<|b|,试把-a,-b,a,b用“<”号连接起来
5.若,则的大小关系是( )
A. B. C. D.
6.有两只小蚂蚁在如图所示的数轴上爬行,蚂蚁甲从图中点A的位置沿数轴向右爬了4个单位长度到达点C处,蚂蚁乙从图中点B的位置沿数轴向左爬了8个单位长度到达点D处。
(1)在图中描出点C. D的位置;
(2)点E到点C与点D的距离相等,在数轴上描出点E的位置,并用“<”把点A. B. C. D. E所表示的数连接起来。
7.操作与探究
(1)比较下列各式的大小(用“<”或“>”或“=”连接)
①| 4|+|5|___|( 4)+5|. ②|4|+|5|___|4+5|.
③|-8|+| 2|___|(-8)+( 2)|. ④|0|+| 7|___|0+( 7)|.
(2)通过以上比较,请你分析、归纳出当a、b为有理数时,比较大小|a|+|b|___|a+b|.
(3)根据(2)中得出的结论,当|x|+2017=|x 2017|时,x的取值范围是___.
1.1 正数和负数
学习目标:
1.了解负数的来源.
2.理解正数、零、负数表示的意义.
3.会用正、负数表示具有相反意义的量.
知识总结:
1.正数与负数
(1)正数:大于 的数.
(2)负数:在正数前加上符号“”(负)的数.
(3)特例:0既不是_____,也不是_____.
2.用正负数表示相反意义的量
增长和减少、高出和低于、收入和支出、盈利和亏损等都是具有_____意义的量,通常增长、高出、收入、盈利等我们用___数表示,而减少、低于、支出、亏损等我们用___数表示.
考点一 正数与负数
例1 判断下列各数哪些是正数,哪些是负数?
+2013,-3.2, ,10.72,-9,+1,-45.6,0, ,-2.14,
课堂训练
1.在1,-2,-5.5,0,,,3.14中,负数的个数为( )
A.3 B.4 C.5 D.6
【互动探究】上题中,正数有几个?里面有没有既不是正数也不是负数的数?
2.下列结论中,正确的是( )
A.0是正数 B.0是最小的正数
C.0是负数 D.现在学的数可分为正数、负数和0三类
考点二 用正负数表示具有相反意义的量
例1 某日林芳在一条东西方向的公路上跑步,她从A地出发,如果向西跑100m记作-100m,那么她折回来又继续跑了110m是什么意思?这时她停下来休息,此时她在A地的什么方向?距A地多远?林芳共跑了多少米?
例2 某中学对初一新生进行立定跳远测试,规定男生能跳170cm及以上为达标,超过170cm的数用正数表示,不足170cm的数用负数表示,第一组10名男生成绩(单位:cm)如下:
求第一组有百分之几的学生达标?
课堂训练
1.李白出生于公元701年,我们记作+701,那么秦始皇出生于公元前259年,可记作( )
A.259 B.-259 C.-957 D.445
2 .每袋大米以50kg为标准,其中超过标准的千克数记为正数,不足的千克数记为负数,则图中第3袋大米的实际重量是___ kg.
3. 某机器零件的设计图纸上写有“”,根据图纸上的信息,判断该零件长度(L)尺寸合格的是( )
A.9.68mm B.9.97mm C.10.1mm D.10.01mm
4. 某公交车原坐18人,经过3人站点时上下车情况如下(上车为正,下车为负):
(+3, 8),(+5, 7),(+4, 2),则现在车上人数还有___.
5. 刘明上周五在股市以收盘价(收市时的价格)每股25元买进某公司股票2000股,在接下来的一周交易日内,小王记下该股票每日收盘价格相比前一天的涨跌情况:(单位:元)
星期 一 二 三 四 五
每股涨跌 +2 -0.5 +1.5 -1.8 +0.8
根据上表回答问题:
(1)星期二收盘时,该股票每股多少元?
(2)本周内该股票收盘时的最高价,最低价分别是多少?
(3)已知买入股票与卖出股票均需支付成交金额的千分之三的交易费.若小王在本周五以收盘价将全部股票卖出,他的收益情况如何?
6.“十一”黄金周,坚胜家电城大力促销,收银情况一直看好.下表为当天与前一天的营业额的涨跌情况.已知9月30日的营业额为26万元.
10月1日 2日 3日 4日 5日 6日 7日
4 3 2 0
(1)黄金周内收入最低的哪一天?直接回答,不必写过程.
(2)黄金周内平均每天的营业额是多少?
拓展探究
7 .有一列数如下:1,0,1,0,0,1,0,0,0,1,0,0,0,0,1,…,则第9个1在这列数中是第______个数。
8.如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动,它从A处出发去看望B,C,D格点处的其他甲虫,规定:向上向右走均为正,向下向左走均为负,如果从A到B记为A→B{1,4},从B到A记为B→A{ 1, 4},其中第一个数表示左右方向移动,第二个数表示上下方向移动。
(1)图中A→C{___,___},C→D{___,___};
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
第一章 有理数
1.2 有理数
学习目标:
1.理解有理数的含义.
2.能够把给出的有理数正确分类.
3.了解0在有理数分类中的作用.
知识总结:
1.有理数:在数学中,我们将_____和_____统称为有理数.
2.有理数的分类
注:①小学学过的π是正数,但不是有理数;
②"四非":即非负数,非负整数,非正数,非正整数(不要丢掉“0”);
③"0"既不是正数也不是负数;
考点一 有理数的有关概念
1.下列说法正确的是( )
A.整数就是正整数和负整数 B.非负整数就是正整数
C.有理数中不是负数就是正数 D.零是自然数,但不是正整数
2.下列说法错误的是( )
A.负整数和负分数统称为负有理数 B.正整数,0,负整数统称为整数
C.正有理数与负有理数组成全体有理数 D.3.14是小数,也是分数
3.有理数-8,20, ,0,-5,+13, ,-7.2中,非负有理数与分数共有( )
A.4个 B.5个 C.6个 D.7个
考点二 有理数的分类
例1 把下列各数填入相应的大括号里:
-5,10,-4.5, ,-2.15,0.01,+66, ,15%, ,,2014,-16.
正整数集合:{ …};
负整数集合:{ …};
负分数集合:{ …};
正分数集合:{ …};
负有理数集合:{ …};
有理数集合:{ …}.
例2 已知有A,B,C三个数的“家族”:
A:{-1,3.1,-4,6,2.1}, B:{-4.2,2.1,-1,10,},
C:{2.1,-4.2,8,6}.
(1)请把每个“家族”中所含的数填入图中的相应部分.
(2)把A,B,C三个数的“家族”中的负数写在横线上:___.
(3)有没有同时属于A,B,C三个数的“家族”的数?若有,则是___.
课堂训练
1.将下列各数填入它属于的集合的圈内:
20,-0.08,,7.6,3.14,-1,,+5.
2.如图,两个圈分别表示正数集合和整数集合,请将3,0,,, 5,3.4中符合条件的数填入圈中。
3.如图所示,今有A,B,C三个数集,每个数集中所包含的数都写在下面的大括号内,请把这些数填入对应的三个圈内.A={3,2,0,4},B={5,6,-5,0,2},C={-5,0,4,-2}.
拓展探究
1.将一串有理数按下列规律排列,回答下列问题.
(1)在A处的数是正数还是负数?
(2)负数排在A,B,C,D中的什么位置?
(3)第2019个数是正数还是负数?排在对应于A,B,C,D中的什么位置?
2.在小学我们学习了偶数0,2,4,6,8,…,以及奇数1,3,5,7,9,…,现在我们学过了负数,也知道了负偶数与负奇数,负偶数 2, 4, 6, 8,…,负奇数 1, 3, 5, 7,…,下面我们将这些负偶数与负奇数排列如图所示:
在上述的这些数中,观察它们的规律,并求 101在哪一列。
第一章 有理数
1.2 数轴
1.定义:规定了原点、正方向和单位长度的直线叫做数轴.
注:①数轴的三要素:原点、正方向、单位长度;
②有理数都能在数轴表示出来,但数轴上的点不都代表有理数,比如π.
例1 四位同学画数轴如下图所示,你认为正确的是( ).
B.
C. D.
例2 点A表示数轴上的一个点,将点A向右移动10个单位,再向左移动6个单位,终点恰好是原点,则点A表示的数是___.
例3 数轴上表示整数的点称为整点,某数轴的单位长度是1厘米,若在这个数轴上随意画出一条长为2020厘米的线段AB,则线段AB盖住的整点个数是()
A.2018或2019 B.2019或2020 C.2020或2021 D.2021或2022
例4 操作探究:已知在纸面上有一数轴(如图所示),
操作一:
(1)折叠纸面,使表示的1点与 1表示的点重合,则 3表示的点与___表示的点重合;
操作二:
(2)折叠纸面,使 1表示的点与3表示的点重合,回答以下问题:
①5表示的点与数___表示的点重合;
②若数轴上A. B两点之间距离为11,(A在B的左侧),且A. B两点经折叠后重合,求A. B两点表示的数是多少。
课堂训练
1.图中所画的数轴,正确的是( )
A. B.
C. D.
2.数轴上点A表示 2,从A出发,沿数轴移动4个单位长度到达点B,则点B表示的数是______.
3.数轴上一点A,一只蚂蚁从A出发爬了4个单位长度到了点3,则点A所表示的数是______.
4.已知点A在数轴上表示的数是-2,点B到原点的距离等于3,则A、B两点间的距离是 。
5.有理数m、n在数轴上的位置如图所示,下列判断正确的是( )
A. m<0 B. m>1 C. n> 1 D. n< 1
6.如图,数轴上有M,N,P,Q四个点,其中点P所表示的数为a,则数 3a所对应的点可能是( )
A. M B. N C. P D. Q
7.如图,在数轴上,点A表示的数为 1,点B表示的数为4,C是点B关于点A的对称点,则点C表示的数为____。
8.已知A,B,C是数轴上的三个点,且C在B的右侧。点A,B表示的数分别是1,3,如图所示。若BC=2AB,则点C表示的数是___.
9.如图,将一刻度尺放在数轴上(数轴的单位长度是1cm),刻度尺上“1cm”和“9cm”分别对应数轴上的 3和x,那么x的值为___.
10.在数轴上,老师不小心把一滴墨水滴在画好的数轴上,如图所示,试根据图中标出的数值判断被墨水盖住的整数有______个.
11.在下面给出的数轴中A表示1,B表示 2.5,回答下面的问题:
(1)A、B之间的距离是___.
(2)观察数轴,与点A的距离为5的点表示的数是:___;
(3)若将数轴折叠,使A点与 2表示的点重合,则B与数___表示的点重合.
(4)若数轴上M、N两点之间的距离为2016(M在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是:M:___,N:___.
12.小敏家、学校、邮局、图书馆坐落在一条东西走向的大街上,依次记为A,B,C,D,学校位于小敏家西150米,邮局位于小敏家东100米,图书馆位于小敏家西400米。
(1)用数轴表示A,B,C,D的位置;
(2)一天小敏从家里先去邮局寄信后,再以每分钟50米的速度往图书馆方向走了约8分钟。试问这时小敏约在什么位置 距图书馆和学校各约多少米
拓展探究
13.如图,圆的周长为4个单位长,数轴每个数字之间的距离为1个单位,在圆的四等分点处分别标上0,1,2,3,先让圆周上表示数字0的点与数轴上表示 1的点重合。再将数轴按逆时针方向环绕在该圆上(如圆周上表示的数字3的点与数轴上表示 2的点重合……),则该数轴上表示 2019的点与圆周上重合的点表示的数字是( )
A. 0 B. 1 C. 2 D. 3
14.等边三角形(三条边都相等的三角形是等边三角形)纸板ABC在数轴上的位置如图所示,点A,B对应的数分别为0和 1,若△ABC绕着顶点顺时针方向在数轴上连续翻转,翻转第1次后,点C所对应的数为1,则翻转2020次后,点C所对应的数是( )
A.2017 B.2018 C.2019 D.2020
第一章 有理数
1.2相反数
1.相反数的定义及其性质
(1)定义:只有符号不同的两个数.特别地,0的相反数是0.一般地,a和-a互为相反数.
(2)求法:在任意一个数的前面添上负号,新的数就表示原数的相反数.
注:①若a与b互为相反数,则a+b=0,反之也成立;
②在数轴上,表示互为相反数的两个点,位于原点的两侧,且到原点的距离相等
2.多重符号的化简
若一个正数前有偶数个负号,结果为正;若一个正数有奇数个负号,结果为负.
例1 下列说法中,正确的是( )
A.因为相反数是成对出现的,所以0没有相反数
B.数轴上原点两旁的两点表示的数是互为相反数
C.符号不同的两个数是互为相反数
D.正数的相反数是负数,负数的相反数是正数
例2 给出下列各组数:①-1与+(-1);②+(+1)与-1;③-(+4)与-(-4);④-(+1.7)与+(-1.7);⑤-[+(-8)]与-[-(+8)]。其中互为相反数的有__________________(填写序号).
例3 若-{-[+(-a)]}与-(+4)互为相反数,则-[+(-a)]=______.
例4 如图,数轴上一动点A向左移动2个单位长度到达点B,再向右移动5个单位长度到达点C.若点C表示的数为1,则与点A表示的数互为相反数的是______.
课堂训练
下列说法中正确的有( )
①π的相反数是-3.14;②符号相反的数互为相反数;③一个数的相反数可能与它相等;④-(-3.8)的相反数是-3.8;⑤正数与负数互为相反数.
2.给出下列各数:+(-10),-(+15),-(-7),-[+(-a)],-[-(-20)].其中相反数一定为负数的有______个.
3.若-a=-(-4),则+[-(-a)]=______.
4.若-[+(-5)]=a,则-a的相反数是______.
5.如果a的相反数是最大的负整数,b的相反数是最小的正整数,则a+b=______.
6.数轴上A和B所表示的点互为相反数,且两个点之间的距离为14,则A和B这两个数分别为______.
7.数轴上点A表示 3,B和C两点所表示的数互为相反数,且点B到点A的距离为3,则点C所表示的数应是______.
8.如图,数轴的单位长度为1,回答下列问题:
(1)如果点A和C表示的数互为相反数,那么点D表示的数是多少
(2)如果点C和E表示的数互为相反数,那么点B和D表示的数是多少
9.已知表示数a的点在数轴上的位置如图所示。
(1)若数a与其相反数相距20个单位长度,则a表示的数是多少
(2)在(1)的条件下,若数b表示的数与数a的相反数表示的点相距5个单位长度,求b表示的数是多少
第一章 有理数
1.2.4绝对值
一.绝对值
(1)定义:数轴上表示数a的点与原点的距离叫做数a的绝对值.
(2)记法:数a的绝对值记作|a|.
(3)代数结论:正数的绝对值是它本身;负数的绝对值是它的相反数;0的绝对值是0.也即
(4)注意:①对任何数a,都有.②若|a|=|b|,则a=b或a=-b.③若|a|+|b|=0,则a=b=0.
二.比较大小
数轴法:数轴上右边的数大于左边的数.
代数法:①正数>0>负数,②两个负数比大小,绝对值大的反而小.
考点一 绝对值
例1 下列说法中正确的个数有( ).
①互为相反数的两个数的绝对值相等;②绝对值等于本身的数只有正数;③不相等的两个数的绝对值不相等;④绝对值相等的两个数一定相等.
A.1个 B.2个 C.3个 D.4个
例2 已知a=-8,|a|=|b|,求b的值.
例3 已知|x 4|+|2y+2|=0,求2x |y|的值。
例4 下列说法正确的是( )
A.如果|a|=|b|,那么a=b B.如果|a|>|b|,那么a>b
C.如果a>|b|,那么a>b D.如果a>b,那么|a|>|b|
例5 阅读下列材料:我们知通|x|的几何意义是数轴上数x的对应点与原点之间的距离,即|x|=|x-0|,也可以说,|x|表示数轴上数x与数0对应点之间的路离。这个结论可以推广为表示数轴上数与数对应点之间的距离.
举例1:已知|x|=2,求x的值.
解:在数轴上与原点距离为2的点表示的数为-2和2,
所以x的值为-2或2.
举例2:已知,求x的值.
解:在数轴上与1对应的点的距离为2的点表示的数为3和-1.
所以x的值为3或-1.
仿照材料中的解法,求下列各式中x的值.
(1)|x|=3; (2)|x+2|=4; (3)|x-3|=|x+1|.
课堂训练
1.下列各组数中,互为相反数的是( )
A. 3与 B.| 3|与3 C.与 D.与
2. 在-2,|-2|,-|-2|,-(-2),-(+2),-|+2|中,负数的个数是_____。
3.若-|-a|=-|-4|,则a= .
4.绝对值大于2且小于5的整数是____.
5.若a,b互为相反数, c,d互为倒数,x的绝对值是1,求的值。
8.下列说法正确的是( )
A. a的绝对值是a B.若|x|= x,则x是负数 C.a的绝对值是a D.若m= n,则|m|=|n|
9.下列判断正确的是( )
A.若|a|=|-b|,则a=b B.若|a|=|b|,则a=-b
C.若a=b,则|a|=|b| D.若a=-b,则|a|=-|b|
10.如图,实数 3,x,3,y在数轴上的对应点分别为M、N、P、Q,这四个数中绝对值最大的数对应的点是( )
A. 点M B. 点N C. 点P D. 点Q
11.如图,四个有理数在数轴上的对应点M,P,N,Q,若点M,P表示的有理数互为相反数,则图中表示绝对值最大的数的点是( )
A.点M B.点N C.点P D.点Q
12.如图,数轴上的A. B. C三点所表示的数分别为a、b、c,其中AB=BC,如果|a|>|b|>|c|,那么该数轴的原点O的位置应该在( )
A.点A的左边 B.点A与点B之间 C.点B与点C之间 D.点C的右边
13.如图,若数轴上a的绝对值是b的绝对值的3倍,则数轴的原点在点______或点______.(填“A”、“B”“C”或“D”)
14.回答下列问题
(1)数轴上表示2和5的两点之间的距离是_____,数轴上表示-2和-5的两点之间的距离是_____,数轴上表示1和-3的两点之间的距离是_____;
(2)数轴上表示x和-1的两点A和B之间的距离|AB|=2,那么x为_____.
考点二 比较大小
例1 在三个有理数a、b、c中,a、b都是负数,c是正数,且|b|>|a|>|c|.
(1)在数轴上表示出a,b,c三个数的大致位置;
(2)比较a,b,c的大小.
课堂训练
1.比较下列各对数的大小:
(1)-(-3)和|-2|; (2) -(-4)和-|-4|;
(3) -|-5|和+(-6); (4) -|+1|和-(+3)
2.若a,b两数在数轴上位置如图所示,将a、b、-a、-b用“<”连接,其中正确的是( )
A.a<-a<b<-b B.-b<a<-a<b C.-a<b<-b<a D.-b<a<b<-a
3.若a,b为有理数,a>0,b<0,且|a|<|b|,则a,b,-a,|b|的大小关系是____
4.己知a>0,b<0,a<|b|,试把-a,-b,a,b用“<”号连接起来
5.若,则的大小关系是( )
A. B. C. D.
6.有两只小蚂蚁在如图所示的数轴上爬行,蚂蚁甲从图中点A的位置沿数轴向右爬了4个单位长度到达点C处,蚂蚁乙从图中点B的位置沿数轴向左爬了8个单位长度到达点D处。
(1)在图中描出点C. D的位置;
(2)点E到点C与点D的距离相等,在数轴上描出点E的位置,并用“<”把点A. B. C. D. E所表示的数连接起来。
7.操作与探究
(1)比较下列各式的大小(用“<”或“>”或“=”连接)
①| 4|+|5|___|( 4)+5|. ②|4|+|5|___|4+5|.
③|-8|+| 2|___|(-8)+( 2)|. ④|0|+| 7|___|0+( 7)|.
(2)通过以上比较,请你分析、归纳出当a、b为有理数时,比较大小|a|+|b|___|a+b|.
(3)根据(2)中得出的结论,当|x|+2017=|x 2017|时,x的取值范围是___.
