2.4生活中的抛体运动 课时作业(word解析版)
文档属性
| 名称 | 2.4生活中的抛体运动 课时作业(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 711.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-10-14 06:19:21 | ||
图片预览




文档简介
2021-2022学年鲁科版(2019)必修第二册
2.4生活中的抛体运动 课时作业(解析版)
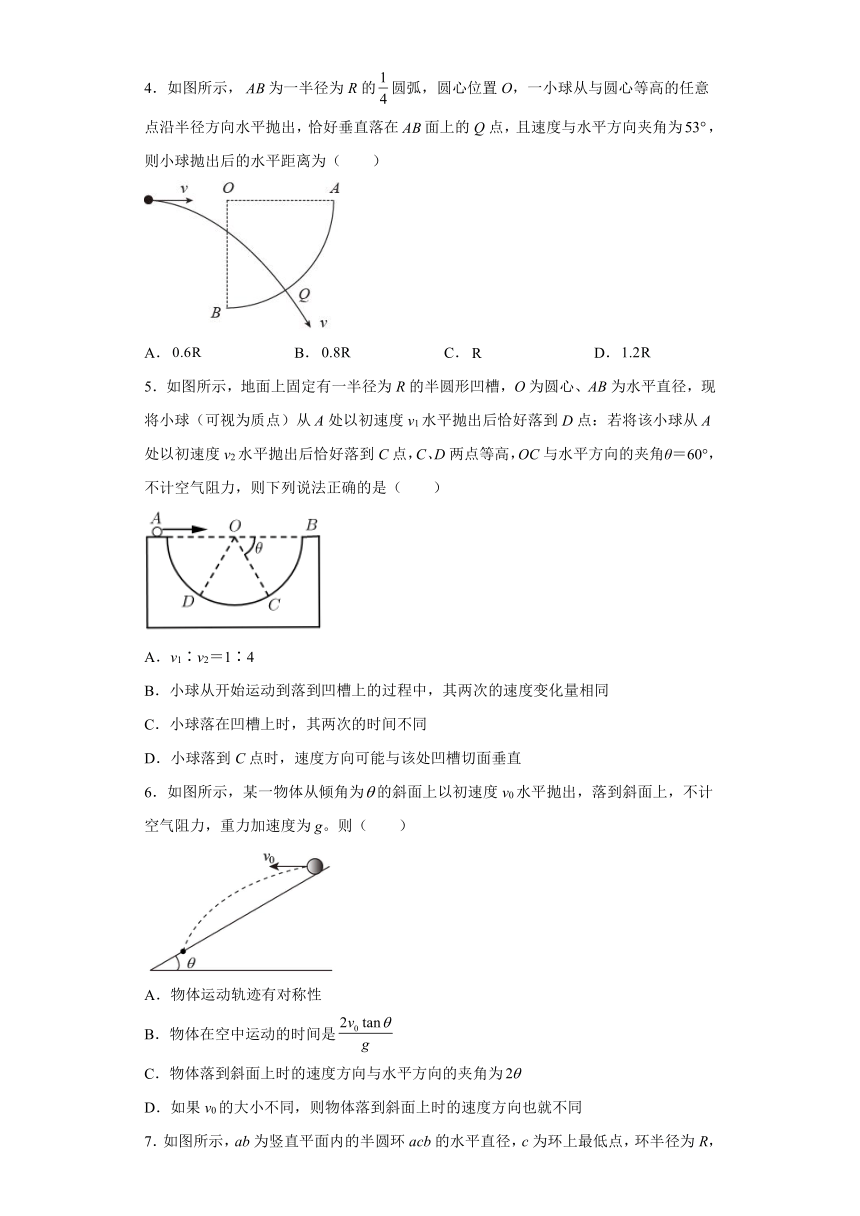
1.如图所示,在同一点抛出四个不同的小球,在空中的运动轨迹如图,不计空气阻力,下面判断正确的是( )
A.球在空中运动时间比球大
B.球在空中的运动时间比球短
C.球与球在空中的运动时间不可能相等
D.球与球在空中的运动时间相等
2.如图所示,将一个小球从M点以初速度vm竖直向上抛出,小球运动过程中还受到恒定的水平作用力,从M点运动到N点时,小球的速度方向恰好改变了90°,则在从M点到N点的运动过程中,小球的速率( )
A.先减小后增大 B.先增大后减小
C.一直增大 D.一直减小
3.如图所示,一斜面固定在高为1.2m的水平桌面上,其下边缘与桌沿对齐。斜面的水平倾角为30°顶端距桌面高度为0.2m。现将一光滑的小球从斜面顶端由静止释放,忽略空气阻力,取重力加速度g=10m/s2,则小球由桌沿到落地的时间为( )
A.0.2s B.0.4s C.0.6s D.0.8s
4.如图所示,为一半径为R的圆弧,圆心位置O,一小球从与圆心等高的任意点沿半径方向水平抛出,恰好垂直落在面上的Q点,且速度与水平方向夹角为,则小球抛出后的水平距离为( )
A. B. C. D.
5.如图所示,地面上固定有一半径为R的半圆形凹槽,O为圆心、AB为水平直径,现将小球(可视为质点)从A处以初速度v1水平抛出后恰好落到D点:若将该小球从A处以初速度v2水平抛出后恰好落到C点,C、D两点等高,OC与水平方向的夹角θ=60°,不计空气阻力,则下列说法正确的是( )
A.v1∶v2=1∶4
B.小球从开始运动到落到凹槽上的过程中,其两次的速度变化量相同
C.小球落在凹槽上时,其两次的时间不同
D.小球落到C点时,速度方向可能与该处凹槽切面垂直
6.如图所示,某一物体从倾角为的斜面上以初速度v0水平抛出,落到斜面上,不计空气阻力,重力加速度为g。则( )
A.物体运动轨迹有对称性
B.物体在空中运动的时间是
C.物体落到斜面上时的速度方向与水平方向的夹角为
D.如果v0的大小不同,则物体落到斜面上时的速度方向也就不同
7.如图所示,ab为竖直平面内的半圆环acb的水平直径,c为环上最低点,环半径为R,将一个小球从a点以初速度沿ab方向抛出,设重力加速度为g,不计空气阻力,则以下说法不正确是( )
A.当小球的初速度时,碰到圆环时的竖直分速度最大
B.当取值不同时,小球落在圆环上的竖直位移可能相同
C.无论取何值,小球都不可能垂直撞击圆环
D.当取值不同时,小球落在圆环上的速度方向和水平方向之间的夹角可以相同
8.关于斜抛运动的说法正确的是( )
A.物体抛出后,速度一直增大 B.是匀变速曲线运动
C.抛出后先做减速运动,在做加速运动 D.斜抛运动的加速度一直减小
9.如图所示,小球甲从点水平抛出,同时将小球乙从点自由释放,两小球先后经过点时的速度大小相等,速度方向夹角为37°。已知、两点的高度差,重力加速度,,。两小球质量相等,不计空气阻力。根据以上条件可知( )
A.小球甲水平抛出的初速度大小为
B.小球甲从点到达点所用的时间为
C.、两点的高度差为
D.两小球在点时重力的瞬时功率相等
10.如图所示,倾角为的固定斜面,其右侧有一竖直墙面,小球滑上斜面,以速度v飞离斜面,恰好垂直撞击到墙面上某位置,重力加速度为g,忽略空气阻力,下列说法中正确的是( )
A.从飞行过程中,小球在水平方向做匀速直线运动,竖直方向做匀减速直线运动
B.竖直墙面与斜面右端的水平距离为
C.竖直墙面与斜面右端的水平距离为
D.从飞离斜面到撞击墙面的过程中,小球竖直上升的高度为
11.如图所示,从倾角为的足够长的斜面顶端P以速度抛出一个小球,落在斜面上某处Q点,小球落在斜面上的速度与斜面的夹角为,若把初速度变为,则以下说法正确的是( )
A.小球在空中的运动时间变为原来的2倍
B.夹角将变大
C.PQ间距一定大于原来间距的4倍
D.夹角与初速度大小有关
12.如图所示,足够长的斜面上有、、、、五个点,,从点水平抛出一个小球,不计空气阻力,当初速度为时,小球落在斜面上的点,落在斜面上时的速度方向与斜面的夹角为;当初速度为时,则( )
A.小球落在斜面上时的速度方向与斜面的夹角大于
B.小球落在斜面上时的速度方向与斜面的夹角也为
C.小球可能落在斜面上的点与点之间
D.小球一定落在斜面上的点
13.在xOy竖直平面内,在空中由A点斜射出一质量为m的粒子,B和C是粒子在空中运动轨迹上的两点,如图所示,其中l0为常数,忽略空气阻力,重力加速度为g,求:
(1)粒子从A到C过程所经历的时间;
(2)粒子经过C点时的速率。
14.一个小球从倾角为θ的斜面上A点以水平速度v0抛出,不计空气阻力,求:
(1) 自抛出至落到斜面需要的时间;
(2) 落到斜面上的B点到抛出点A的距离;
(3) 落到斜面上的B点时的速度.
15.跳台滑雪是滑雪爱好者喜欢的一种运动,某滑雪轨道可以简化成如图所示的示意图.其中助滑雪道CB段与水平方向夹角α=30°,BO段是水平起跳台,OA段是着陆雪道, CB段与BO段用一小段光滑圆弧相连,运动员从助滑雪道CB上的C点在自身重力作用下由静止开始运动,滑到O点水平飞出,不计空气阻力,经2s在水平方向飞行了40m,落在着陆雪道上的A点,已知运动员和装备的总质量为50kg,C点距O点的竖直高度为25m(g取10m/s2)求:
(1)运动员离开O点时的速度大小;
(2)运动员即将落到A点时的速度大小;
(3)运动员经过CO段过程中减少的机械能
16.如图所示,在水平地面上固定一倾角的斜面体ABC, AC长为=3m,A正上方一小物体距离地面高h=2.7m,将物体以水平速度向右抛出,不计空气阻力,已知sin37°=0.6,cos37°=0.8,g=10m/s2
(1)若物体恰好击中斜面AC中点,求大小;
(2)若物体以=4m/s水平抛出,求物体击中斜面体ABC前飞行时间。
参考答案
1.A
【详解】
斜抛运动可看成两个方向相反的平抛运动,由于平抛运动在空中运动的时间取决于高度,则斜抛运动在空中运动时间也取决于高度,由图可知,球的最大高度比球大,则球在空中运动时间比球大,同理可知,球在空中的运动时间比球大,球与球在空中的运动时间相等,球比球在空中的运动时间大。
故选A。
2.A
【详解】
对小球受力分析,可知重力竖直向下,恒力水平向右,即合力方向斜向右下,从图中小球轨迹可知,开始一段时间,速度与合力成钝角,小球速度减小,后来速度与合力夹角为锐角,小球速度增加。
故选A。
3.B
【详解】
小球由斜面顶端到达桌沿的过程由机械能守恒定律
解得
v=2m/s
小球从桌沿飞出时的竖直分速度为
根据
解得
t=0.4s
故选B。
4.D
【详解】
如图所示,小球恰好垂直落在面上的Q点,作速度的反向延长线,交于O点,由平抛运动的推论可知,速度反向延长线交水平位移的中点,故满足
结合圆的几何关系可得
联立可解得,D正确。
故选D。
5.B
【详解】
A.过C与D分别做AB的垂线,交AB分别与M点与N点,如图
则
OM=ON=R·cos60°=0.5R
所以
AM=1.5R,AN=0.5R
由于C与D点的高度是相等的,由h=gt2可知二者运动的时间是相等的。由水平方向的位移为
x=v0t
可得
故A错误;
B.它们速度的变化量
△v=gt
二者运动的时间是相等的,则它们速度的变化量也相等,故B正确;
C.两次的竖直位移分相同,所以前后两次的时间相等,故C错误;
D.球落到C点时,若速度方向与该处凹槽切面垂直则速度方向为OC,O点应为AM的中点,显然不是,故D错误。
故选B。
6.B
【详解】
A.平抛运动轨迹没有对称性,所以A错误;
B.物体落在斜面上时,斜面倾角为位移与水平方向的夹角为
则物体在空中运动的时间是
所以B正确;
CD.物体落到斜面上时的速度方向与水平方向的夹角
即物体落到斜面上时的速度方向与v0大小无关,所以CD错误;
故选B。
7.D
【详解】
A.经分析可知当小球落在c点时间最长,竖直分速度最大。对竖直方向
对水平方向
故A不符合题意;
B.当取不同值时,小球有可能落在圆环上相对于c点对称的两个点,即小球落在圆环上的竖直位移可能相同,故B不符合题意;
C.要使小球垂直撞击半圆环,设小球落点与圆心的连线与水平方向夹角为θ,根据平抛运动规律可知
联立可得
即垂直撞击到b点,这是不可能的,故C不符合题意;
D.取值不同,小球掉到环上时的速度方向和水平方向之间的夹角不相同,故D符合题意。
故选D。
8.BC
【详解】
AC.斜抛运动可以看成竖直和水平两个方向的分运动,竖直方向上是竖直上抛运动,水平方向上是匀速直线运动,所以由矢量的合成可知合速度先减小,后增大,在最高点竖直方向上速度为零,水平方向速度不变,所以合速度为开始运动时的水平分速度;又因为斜抛运动只受重力,所以加速度不变,故A错误,C正确;
BD.物体抛出后,速度沿轨迹的切线方向,因为斜抛运动只受重力,所以加速度为自由落体加速度g,即加速度不变且竖直向下,是匀变速曲线运动,故B正确,D错误。
故选BC。
9.ABC
【详解】
A.小球乙到C的速度为
此时小球甲的速度大小也为,又因为小球甲速度与竖直方向成角,可知水平分速度为
故A正确;
B.根据
计算得小球甲从点到达点所用的时间为,故B正确;
C.、C两点的高度差为
故、两点的高度差为
故C正确;
D.由于两球在竖直方向上的速度不相等,所以两小球在C点时重力的瞬时功率也不相等。故D错。
故选ABC。
10.AC
【详解】
A.小球飞离斜面后做斜上抛运动,只受重力作用,则从飞离斜面到撞击墙面的过程中,小球在水平方向做匀速直线运动,竖直方向做匀减速直线运动,选项A正确;
BCD.小球离开斜面的竖直分速度为vsinα,水平分速度vcosα,则飞行时间
水平距离
小球竖直上升的高度为
故选项C正确,BD错误;
故选AC。
11.AC
【详解】
A.根据
得
初速度变为原来的2倍,则小球在空中的运动时间变为原来的2倍,A正确;
BD.速度与水平方向夹角的正切值
又
故可知速度方向与水平方向夹角正切值是位移与水平方向夹角正切值的2倍。因为位移与水平方向夹角不变,则速度与水平方向夹角不变,所以两个角度之差,即不变,与初速度无关,BD错误;
C.根据
知,初速度变为原来的2倍,则水平位移变为原来的4倍,则PQ间距变为原来的4倍,C正确。
故选AC。
12.BD
【详解】
AB.当小球的初速度变化时,小球落在斜面上的位移方向与水平方向的夹角不变,由平抛运动的推论可知,速度方向与水平方向夹角的正切值为位移方向与水平方向夹角正切值的2倍,即当初速度为时,小球落在斜面上时的速度方向与斜面的夹角也为,A错误,B正确;
CD.设斜面倾角为,则有
解得
则小球在竖直方向上的位移
当初速度变为原来的2倍时,小球在竖直方向上的位移变为原来的4倍,所以小球一定落在斜面上的点,C错误,D正确。
故选BD。
13.(1) (2)
【详解】
(1)设抛物线方程为
y=ax2+c
当y=0时
x=l0
代入上式得
0=al02+c
当x=2l0时
y=-3l0
代入上式得
-3l0=4al02+c
联立可得
c=l0
可得
当x=0时
y=l0
所以最高点离x轴的高度为
h=l0
从最高点到C做平抛运动,则从最高点到B点,根据
可得
从最高点到C点有
解得
故质点从A到C过程所经历的时间
(2)设质点通过最高点的速率为v,则有
从最高点到C点,根据动能定理
解得
14.(1) ;(2) ;(3) ,速度方向与的夹角为,
【详解】
解:(1)水平方向上有:
竖直方向上有:
联立可得自抛出至落到斜面需要时间:
(2)落点到抛出点的距离:
(3)落到斜面上时,竖直分速度:
落到斜面上速度的大小:
设速度方向与的夹角为,则有:
15.(1)20m/s(2)20m/s(3)2500J
【详解】
(1)运动员离开O点时的速度
代入数据解得:
(2)运动员即将着陆时
水平速度
竖直速度
(3)整个过程产生的热能即为CO段损失的机械能
由功能关系得:
带入数据解得=2500J
16.(1)2m/s;(2)s
【详解】
(1)从抛出到C点,由平抛运动的规律得
联立解得
(2)物体以=4m/s水平抛出,设打在斜面上D点,AD长度为,则有
联立解得
2.4生活中的抛体运动 课时作业(解析版)
1.如图所示,在同一点抛出四个不同的小球,在空中的运动轨迹如图,不计空气阻力,下面判断正确的是( )
A.球在空中运动时间比球大
B.球在空中的运动时间比球短
C.球与球在空中的运动时间不可能相等
D.球与球在空中的运动时间相等
2.如图所示,将一个小球从M点以初速度vm竖直向上抛出,小球运动过程中还受到恒定的水平作用力,从M点运动到N点时,小球的速度方向恰好改变了90°,则在从M点到N点的运动过程中,小球的速率( )
A.先减小后增大 B.先增大后减小
C.一直增大 D.一直减小
3.如图所示,一斜面固定在高为1.2m的水平桌面上,其下边缘与桌沿对齐。斜面的水平倾角为30°顶端距桌面高度为0.2m。现将一光滑的小球从斜面顶端由静止释放,忽略空气阻力,取重力加速度g=10m/s2,则小球由桌沿到落地的时间为( )
A.0.2s B.0.4s C.0.6s D.0.8s
4.如图所示,为一半径为R的圆弧,圆心位置O,一小球从与圆心等高的任意点沿半径方向水平抛出,恰好垂直落在面上的Q点,且速度与水平方向夹角为,则小球抛出后的水平距离为( )
A. B. C. D.
5.如图所示,地面上固定有一半径为R的半圆形凹槽,O为圆心、AB为水平直径,现将小球(可视为质点)从A处以初速度v1水平抛出后恰好落到D点:若将该小球从A处以初速度v2水平抛出后恰好落到C点,C、D两点等高,OC与水平方向的夹角θ=60°,不计空气阻力,则下列说法正确的是( )
A.v1∶v2=1∶4
B.小球从开始运动到落到凹槽上的过程中,其两次的速度变化量相同
C.小球落在凹槽上时,其两次的时间不同
D.小球落到C点时,速度方向可能与该处凹槽切面垂直
6.如图所示,某一物体从倾角为的斜面上以初速度v0水平抛出,落到斜面上,不计空气阻力,重力加速度为g。则( )
A.物体运动轨迹有对称性
B.物体在空中运动的时间是
C.物体落到斜面上时的速度方向与水平方向的夹角为
D.如果v0的大小不同,则物体落到斜面上时的速度方向也就不同
7.如图所示,ab为竖直平面内的半圆环acb的水平直径,c为环上最低点,环半径为R,将一个小球从a点以初速度沿ab方向抛出,设重力加速度为g,不计空气阻力,则以下说法不正确是( )
A.当小球的初速度时,碰到圆环时的竖直分速度最大
B.当取值不同时,小球落在圆环上的竖直位移可能相同
C.无论取何值,小球都不可能垂直撞击圆环
D.当取值不同时,小球落在圆环上的速度方向和水平方向之间的夹角可以相同
8.关于斜抛运动的说法正确的是( )
A.物体抛出后,速度一直增大 B.是匀变速曲线运动
C.抛出后先做减速运动,在做加速运动 D.斜抛运动的加速度一直减小
9.如图所示,小球甲从点水平抛出,同时将小球乙从点自由释放,两小球先后经过点时的速度大小相等,速度方向夹角为37°。已知、两点的高度差,重力加速度,,。两小球质量相等,不计空气阻力。根据以上条件可知( )
A.小球甲水平抛出的初速度大小为
B.小球甲从点到达点所用的时间为
C.、两点的高度差为
D.两小球在点时重力的瞬时功率相等
10.如图所示,倾角为的固定斜面,其右侧有一竖直墙面,小球滑上斜面,以速度v飞离斜面,恰好垂直撞击到墙面上某位置,重力加速度为g,忽略空气阻力,下列说法中正确的是( )
A.从飞行过程中,小球在水平方向做匀速直线运动,竖直方向做匀减速直线运动
B.竖直墙面与斜面右端的水平距离为
C.竖直墙面与斜面右端的水平距离为
D.从飞离斜面到撞击墙面的过程中,小球竖直上升的高度为
11.如图所示,从倾角为的足够长的斜面顶端P以速度抛出一个小球,落在斜面上某处Q点,小球落在斜面上的速度与斜面的夹角为,若把初速度变为,则以下说法正确的是( )
A.小球在空中的运动时间变为原来的2倍
B.夹角将变大
C.PQ间距一定大于原来间距的4倍
D.夹角与初速度大小有关
12.如图所示,足够长的斜面上有、、、、五个点,,从点水平抛出一个小球,不计空气阻力,当初速度为时,小球落在斜面上的点,落在斜面上时的速度方向与斜面的夹角为;当初速度为时,则( )
A.小球落在斜面上时的速度方向与斜面的夹角大于
B.小球落在斜面上时的速度方向与斜面的夹角也为
C.小球可能落在斜面上的点与点之间
D.小球一定落在斜面上的点
13.在xOy竖直平面内,在空中由A点斜射出一质量为m的粒子,B和C是粒子在空中运动轨迹上的两点,如图所示,其中l0为常数,忽略空气阻力,重力加速度为g,求:
(1)粒子从A到C过程所经历的时间;
(2)粒子经过C点时的速率。
14.一个小球从倾角为θ的斜面上A点以水平速度v0抛出,不计空气阻力,求:
(1) 自抛出至落到斜面需要的时间;
(2) 落到斜面上的B点到抛出点A的距离;
(3) 落到斜面上的B点时的速度.
15.跳台滑雪是滑雪爱好者喜欢的一种运动,某滑雪轨道可以简化成如图所示的示意图.其中助滑雪道CB段与水平方向夹角α=30°,BO段是水平起跳台,OA段是着陆雪道, CB段与BO段用一小段光滑圆弧相连,运动员从助滑雪道CB上的C点在自身重力作用下由静止开始运动,滑到O点水平飞出,不计空气阻力,经2s在水平方向飞行了40m,落在着陆雪道上的A点,已知运动员和装备的总质量为50kg,C点距O点的竖直高度为25m(g取10m/s2)求:
(1)运动员离开O点时的速度大小;
(2)运动员即将落到A点时的速度大小;
(3)运动员经过CO段过程中减少的机械能
16.如图所示,在水平地面上固定一倾角的斜面体ABC, AC长为=3m,A正上方一小物体距离地面高h=2.7m,将物体以水平速度向右抛出,不计空气阻力,已知sin37°=0.6,cos37°=0.8,g=10m/s2
(1)若物体恰好击中斜面AC中点,求大小;
(2)若物体以=4m/s水平抛出,求物体击中斜面体ABC前飞行时间。
参考答案
1.A
【详解】
斜抛运动可看成两个方向相反的平抛运动,由于平抛运动在空中运动的时间取决于高度,则斜抛运动在空中运动时间也取决于高度,由图可知,球的最大高度比球大,则球在空中运动时间比球大,同理可知,球在空中的运动时间比球大,球与球在空中的运动时间相等,球比球在空中的运动时间大。
故选A。
2.A
【详解】
对小球受力分析,可知重力竖直向下,恒力水平向右,即合力方向斜向右下,从图中小球轨迹可知,开始一段时间,速度与合力成钝角,小球速度减小,后来速度与合力夹角为锐角,小球速度增加。
故选A。
3.B
【详解】
小球由斜面顶端到达桌沿的过程由机械能守恒定律
解得
v=2m/s
小球从桌沿飞出时的竖直分速度为
根据
解得
t=0.4s
故选B。
4.D
【详解】
如图所示,小球恰好垂直落在面上的Q点,作速度的反向延长线,交于O点,由平抛运动的推论可知,速度反向延长线交水平位移的中点,故满足
结合圆的几何关系可得
联立可解得,D正确。
故选D。
5.B
【详解】
A.过C与D分别做AB的垂线,交AB分别与M点与N点,如图
则
OM=ON=R·cos60°=0.5R
所以
AM=1.5R,AN=0.5R
由于C与D点的高度是相等的,由h=gt2可知二者运动的时间是相等的。由水平方向的位移为
x=v0t
可得
故A错误;
B.它们速度的变化量
△v=gt
二者运动的时间是相等的,则它们速度的变化量也相等,故B正确;
C.两次的竖直位移分相同,所以前后两次的时间相等,故C错误;
D.球落到C点时,若速度方向与该处凹槽切面垂直则速度方向为OC,O点应为AM的中点,显然不是,故D错误。
故选B。
6.B
【详解】
A.平抛运动轨迹没有对称性,所以A错误;
B.物体落在斜面上时,斜面倾角为位移与水平方向的夹角为
则物体在空中运动的时间是
所以B正确;
CD.物体落到斜面上时的速度方向与水平方向的夹角
即物体落到斜面上时的速度方向与v0大小无关,所以CD错误;
故选B。
7.D
【详解】
A.经分析可知当小球落在c点时间最长,竖直分速度最大。对竖直方向
对水平方向
故A不符合题意;
B.当取不同值时,小球有可能落在圆环上相对于c点对称的两个点,即小球落在圆环上的竖直位移可能相同,故B不符合题意;
C.要使小球垂直撞击半圆环,设小球落点与圆心的连线与水平方向夹角为θ,根据平抛运动规律可知
联立可得
即垂直撞击到b点,这是不可能的,故C不符合题意;
D.取值不同,小球掉到环上时的速度方向和水平方向之间的夹角不相同,故D符合题意。
故选D。
8.BC
【详解】
AC.斜抛运动可以看成竖直和水平两个方向的分运动,竖直方向上是竖直上抛运动,水平方向上是匀速直线运动,所以由矢量的合成可知合速度先减小,后增大,在最高点竖直方向上速度为零,水平方向速度不变,所以合速度为开始运动时的水平分速度;又因为斜抛运动只受重力,所以加速度不变,故A错误,C正确;
BD.物体抛出后,速度沿轨迹的切线方向,因为斜抛运动只受重力,所以加速度为自由落体加速度g,即加速度不变且竖直向下,是匀变速曲线运动,故B正确,D错误。
故选BC。
9.ABC
【详解】
A.小球乙到C的速度为
此时小球甲的速度大小也为,又因为小球甲速度与竖直方向成角,可知水平分速度为
故A正确;
B.根据
计算得小球甲从点到达点所用的时间为,故B正确;
C.、C两点的高度差为
故、两点的高度差为
故C正确;
D.由于两球在竖直方向上的速度不相等,所以两小球在C点时重力的瞬时功率也不相等。故D错。
故选ABC。
10.AC
【详解】
A.小球飞离斜面后做斜上抛运动,只受重力作用,则从飞离斜面到撞击墙面的过程中,小球在水平方向做匀速直线运动,竖直方向做匀减速直线运动,选项A正确;
BCD.小球离开斜面的竖直分速度为vsinα,水平分速度vcosα,则飞行时间
水平距离
小球竖直上升的高度为
故选项C正确,BD错误;
故选AC。
11.AC
【详解】
A.根据
得
初速度变为原来的2倍,则小球在空中的运动时间变为原来的2倍,A正确;
BD.速度与水平方向夹角的正切值
又
故可知速度方向与水平方向夹角正切值是位移与水平方向夹角正切值的2倍。因为位移与水平方向夹角不变,则速度与水平方向夹角不变,所以两个角度之差,即不变,与初速度无关,BD错误;
C.根据
知,初速度变为原来的2倍,则水平位移变为原来的4倍,则PQ间距变为原来的4倍,C正确。
故选AC。
12.BD
【详解】
AB.当小球的初速度变化时,小球落在斜面上的位移方向与水平方向的夹角不变,由平抛运动的推论可知,速度方向与水平方向夹角的正切值为位移方向与水平方向夹角正切值的2倍,即当初速度为时,小球落在斜面上时的速度方向与斜面的夹角也为,A错误,B正确;
CD.设斜面倾角为,则有
解得
则小球在竖直方向上的位移
当初速度变为原来的2倍时,小球在竖直方向上的位移变为原来的4倍,所以小球一定落在斜面上的点,C错误,D正确。
故选BD。
13.(1) (2)
【详解】
(1)设抛物线方程为
y=ax2+c
当y=0时
x=l0
代入上式得
0=al02+c
当x=2l0时
y=-3l0
代入上式得
-3l0=4al02+c
联立可得
c=l0
可得
当x=0时
y=l0
所以最高点离x轴的高度为
h=l0
从最高点到C做平抛运动,则从最高点到B点,根据
可得
从最高点到C点有
解得
故质点从A到C过程所经历的时间
(2)设质点通过最高点的速率为v,则有
从最高点到C点,根据动能定理
解得
14.(1) ;(2) ;(3) ,速度方向与的夹角为,
【详解】
解:(1)水平方向上有:
竖直方向上有:
联立可得自抛出至落到斜面需要时间:
(2)落点到抛出点的距离:
(3)落到斜面上时,竖直分速度:
落到斜面上速度的大小:
设速度方向与的夹角为,则有:
15.(1)20m/s(2)20m/s(3)2500J
【详解】
(1)运动员离开O点时的速度
代入数据解得:
(2)运动员即将着陆时
水平速度
竖直速度
(3)整个过程产生的热能即为CO段损失的机械能
由功能关系得:
带入数据解得=2500J
16.(1)2m/s;(2)s
【详解】
(1)从抛出到C点,由平抛运动的规律得
联立解得
(2)物体以=4m/s水平抛出,设打在斜面上D点,AD长度为,则有
联立解得
同课章节目录
- 第1章 功和机械能
- 导入 神奇之能
- 第1节 机械功
- 第2节 功率
- 第3节 动能和动能定理
- 第4节 势能及其改变
- 第5节 科学验证:机械能守恒定律
- 第2章 抛体运动
- 导入 更准、更远
- 第1节 运动的合成与分解
- 第2节 平抛运动
- 第3节 科学探究:平抛运动的特点
- 第4节 生活中的抛体运动
- 第3章 圆周运动
- 导入 生活中的圆周运动
- 第1节 匀速圆周运动快慢的描述
- 第2节 科学探究:向心力
- 第3节 离心现象
- 第4章 万有引力定律及航天
- 导入 从嫦娥奔月到“阿波罗”上天
- 第2节 万有引力定律的应用
- 第3节 人类对太空的不懈探索
- 第5章 科学进步无止境
- 导入 再次跨越时空的对话
- 第1节 初识相对论
- 第2节 相对论中的神奇时空
- 第3节 探索宇宙的奥秘
