2021-2022学年湘教版数学八年级下册第3章图形语坐标测试卷(word版、含答案)
文档属性
| 名称 | 2021-2022学年湘教版数学八年级下册第3章图形语坐标测试卷(word版、含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 110.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-14 00:00:00 | ||
图片预览



文档简介
第3章达标测试卷
一、选择题(每题3分,共24分)
1.在平面直角坐标系中,点(-3,-a2-1)一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.在平面直角坐标系中的第三象限内有一点P,点P到x轴的距离为2,到y轴的距离为3,则点P的坐标为( )
A.(2,-3) B.(-3,-2) C.(2,3) D.(3,2)
3.点A(3,5)关于x轴的对称点的坐标为( )
A.(3,-5) B.(-3,-5) C.(-3,5) D.(-5,3)
4.将点A(-3,2)向右平移3个单位得到点A′,则点A′的坐标是( )
A.(-6,2) B.(0,2) C.(3,2) D.(-3,5)
5.在直角坐标系中,坐标是整数的点称作格点,第一象限的格点P(x,y)满足2x+3y=7,则满足条件的点有( )
A.1个 B.2个 C.3个 D.4个
6.若点P(a,1)关于y轴的对称点为Q(2,b),则a+b的值是( )
A.-1 B.0 C.1 D.2
7.为了保障艺术节表演的整体效果,某校在操场中标记了几个关键位置,如图是利用平面直角坐标系画出的关键位置分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,点A的坐标为(1,-1),点B的坐标为(3,2),则表示其他位置的点的坐标正确的是( )
A.C(-1,0) B.D(-3,1)
C.E(-2,-5) D.F(5,2)
8.如图,已知: AOCD有一个顶点为O(0,0),顶点C在x轴的正半轴上.按以下步骤作图:
①以点O为圆心,适当长为半径画弧,分别交OA于点M,交OC于点N.
②分别以点M,N为圆心,大于MN的长为半径画弧,两弧在∠AOC内相交于点E.
③画射线OE,交AD于点F(2,3).则点A的坐标为( )
A. B.(3-,3) C. D.(2-,3)
INCLUDEPICTURE"image206.tif" INCLUDEPICTURE "E:\\22春\\8数XJ\\image206.tif" \* MERGEFORMATINET INCLUDEPICTURE "E:\\22春\\8数XJ\\image206.tif" \* MERGEFORMATINET
二、填空题(每题4分,共32分)
9.已知点P的坐标为(1,-2),则点P到x轴的距离是________.
10.在平面直角坐标系中,点A,B的坐标分别为(4,0),(0,3),则线段AB长为________.
11.如图,线段OB,OC,OA的长度分别是1,2,3,且OC平分∠AOB,若将A点表示为(3,30°),B点表示为(1,120°),则C点可表示为________.
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-21.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-21.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-21.tif" \* MERGEFORMATINET
12.已知点P(a+3,2a+4)在y轴上,则点P的坐标为________.
13.在平面直角坐标系中,点A在第一象限,点B在x轴的正半轴上,∠AOB=60°,OA=8.点A的坐标是________.
14.在平面直角坐标系中,对于平面内任意一点(x,y),若规定以下两种变换:
①f(x,y)=(x+2,y);②g(x,y)=(-x,-y).
例如按照以上变换有f(1,1)=(3,1);g(f(1,1))=g(3,1)=(-3,-1).
则f(g(2,5))=________.
15.一只小虫在小方格组成的网格线上爬行,它的起始位置是点A(2,2),先爬到点B(2,4),再爬到点C(5,4),最后爬到点D(5,6),则小虫共爬了________个单位.
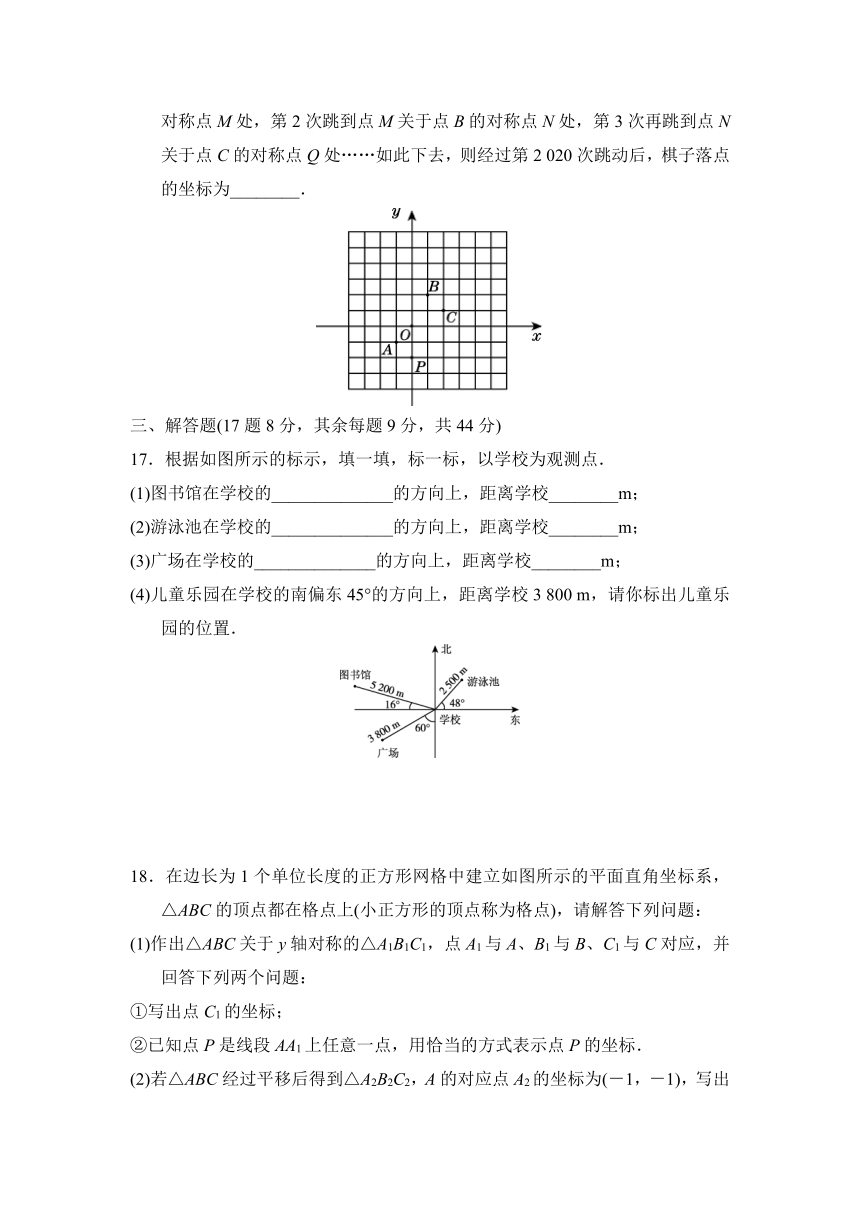
16.如图,在平面直角坐标系中,一颗棋子从点P(0,-2)处开始依次关于点A(-1,-1),B(1,2),C(2,1)作循环对称跳动,即第1次跳到点P关于点A的对称点M处,第2次跳到点M关于点B的对称点N处,第3次再跳到点N关于点C的对称点Q处……如此下去,则经过第2 020次跳动后,棋子落点的坐标为________.
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\DDXX240.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\DDXX240.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\DDXX240.tif" \* MERGEFORMATINET
三、解答题(17题8分,其余每题9分,共44分)
17.根据如图所示的标示,填一填,标一标,以学校为观测点.
(1)图书馆在学校的______________的方向上,距离学校________m;
(2)游泳池在学校的______________的方向上,距离学校________m;
(3)广场在学校的______________的方向上,距离学校________m;
(4)儿童乐园在学校的南偏东45°的方向上,距离学校3 800 m,请你标出儿童乐园的位置.
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\DDXX241.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\DDXX241.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\DDXX241.tif" \* MERGEFORMATINET
18.在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上(小正方形的顶点称为格点),请解答下列问题:
(1)作出△ABC关于y轴对称的△A1B1C1,点A1与A、B1与B、C1与C对应,并回答下列两个问题:
①写出点C1的坐标;
②已知点P是线段AA1上任意一点,用恰当的方式表示点P的坐标.
(2)若△ABC经过平移后得到△A2B2C2,A的对应点A2的坐标为(-1,-1),写出点B的对应点B2的坐标.
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ443.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ443.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ443.tif" \* MERGEFORMATINET
19.若点M(3a-9,1-a)是平面直角坐标系中第三象限的整数点(横、纵坐标都为整数).
(1)求a的值;
(2)求点M向右平移3个单位得到的点M1的坐标.
20.在平面直角坐标系中,点A关于x轴对称的点的坐标为(x+2y-3,y-x+2),点A关于y轴对称的点的坐标为(2y+2x+1,2x-y+2),求x,y的值.
21.在如图所示的平面直角坐标系中,已知A(0,a),B(b,0),C(3,c)三点,若a,b,c满足关系式:|a-2|+(b-3)2+=0.
(1)求a,b,c的值;
(2)求四边形AOBC的面积;
(3)是否存在点P,使△AOP的面积为四边形AOBC的面积的2倍?若存在,求出点P的坐标,若不存在,请说明理由.
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-22.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-22.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-22.tif" \* MERGEFORMATINET
答案
一、1.C 2.B 3.A 4.B 5.A
6.A 点拨:∵点P(a,1)关于y轴的对称点为Q(2,b),∴a=-2,b=1,则a+b=-2+1=-1.
7.B
8.A
二、9.2 点拨:∵点(a,b)到x轴的距离为|b|,∴点P(1,-2)到x轴的距离为2.
10.5 点拨:∵点A,B的坐标分别为(4,0),(0,3),
∴BO=3,AO=4,∴AB==5.
11.(2,75°)
12.(0,-2) 点拨:∵点P(a+3,2a+4)在y轴上,
∴a+3=0,解得a=-3,∴2a+4=-2,则点P的坐标为(0,-2).
13.(4,4 )
14.(0,-5) 点拨: f(g(2,5))=f(-2,-5)=(-2+2,-5)=(0,-5).
15.7 点拨:从点A(2,2)爬到点B(2,4),爬了4-2=2(个)单位,再爬到点C(5,4),爬了5-2=3(个)单位,最后爬到点D(5,6),爬了6-4=2(个)单位,所以小虫一共爬了2+3+2=7(个)单位.
16.(-2,0) 点拨:连接PA并延长到M,使AM=PA,所以M的坐标是(-2,0);连接MB并延长到N,使BN=MB,所以N的坐标是(4,4);连接NC并延长到Q,使CQ=NC,发现Q与P点重合,即棋子跳动3次后又回到点P处.因为2 020÷3=673……1,所以经过第2 020次跳动后,棋子落在点M处,故答案为(-2,0).
三、17.解:(1)北偏西74°;5 200
(2)北偏东42°;2 500
(3)南偏西60°;3 800
(4)儿童乐园的位置如图所示.
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\DDXX325.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\DDXX325.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\DDXX325.tif" \* MERGEFORMATINET
18.解:(1)如图所示.
①点C1的坐标为(-3,2);
②点P的坐标为(x,4)(-2≤x≤2).
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ643.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ643.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ643.tif" \* MERGEFORMATINET
(2)点B2的坐标为(-2,-4).
19.解:(1)∵点M(3a-9,1-a)是第三象限的整数点,
∴3a-9<0,1-a<0,∴1<a<3.
∵点M的横、纵坐标都为整数,∴a=2.
(2)当a=2时,3a-9=-3,1-a=-1,
∴点M的坐标是(-3,-1).
则点M向右平移3个单位得到的点M1的坐标为(0,-1).
20.解:∵点A关于x轴对称的点的坐标为(x+2y-3,y-x+2),
∴A点坐标为(x+2y-3,-y+x-2).
∵点A关于y轴对称的点的坐标为(2y+2x+1,2x-y+2),
∴A点坐标为(-2y-2x-1,2x-y+2),
∴解得
21.解:(1)∵|a-2|+(b-3)2+=0,
∴a-2=0,b-3=0,c-4=0,
∴a=2,b=3,c=4.
(2)由(1)知A(0,2),O(0,0),B(3,0),C(3,4),
∴四边形AOBC为直角梯形,且OA=2,BC=4,OB=3,
∴四边形AOBC的面积=×(OA+BC)·OB=×(2+4)×3=9.
(3)存在.∵△AOP的面积为四边形AOBC的面积的2倍,
∴△AOP的面积=×2×|x|=2×9,
∴|x|=18,∴x=±18.
∴点P的坐标为(18,-9)或(-18,9).
一、选择题(每题3分,共24分)
1.在平面直角坐标系中,点(-3,-a2-1)一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.在平面直角坐标系中的第三象限内有一点P,点P到x轴的距离为2,到y轴的距离为3,则点P的坐标为( )
A.(2,-3) B.(-3,-2) C.(2,3) D.(3,2)
3.点A(3,5)关于x轴的对称点的坐标为( )
A.(3,-5) B.(-3,-5) C.(-3,5) D.(-5,3)
4.将点A(-3,2)向右平移3个单位得到点A′,则点A′的坐标是( )
A.(-6,2) B.(0,2) C.(3,2) D.(-3,5)
5.在直角坐标系中,坐标是整数的点称作格点,第一象限的格点P(x,y)满足2x+3y=7,则满足条件的点有( )
A.1个 B.2个 C.3个 D.4个
6.若点P(a,1)关于y轴的对称点为Q(2,b),则a+b的值是( )
A.-1 B.0 C.1 D.2
7.为了保障艺术节表演的整体效果,某校在操场中标记了几个关键位置,如图是利用平面直角坐标系画出的关键位置分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,点A的坐标为(1,-1),点B的坐标为(3,2),则表示其他位置的点的坐标正确的是( )
A.C(-1,0) B.D(-3,1)
C.E(-2,-5) D.F(5,2)
8.如图,已知: AOCD有一个顶点为O(0,0),顶点C在x轴的正半轴上.按以下步骤作图:
①以点O为圆心,适当长为半径画弧,分别交OA于点M,交OC于点N.
②分别以点M,N为圆心,大于MN的长为半径画弧,两弧在∠AOC内相交于点E.
③画射线OE,交AD于点F(2,3).则点A的坐标为( )
A. B.(3-,3) C. D.(2-,3)
INCLUDEPICTURE"image206.tif" INCLUDEPICTURE "E:\\22春\\8数XJ\\image206.tif" \* MERGEFORMATINET INCLUDEPICTURE "E:\\22春\\8数XJ\\image206.tif" \* MERGEFORMATINET
二、填空题(每题4分,共32分)
9.已知点P的坐标为(1,-2),则点P到x轴的距离是________.
10.在平面直角坐标系中,点A,B的坐标分别为(4,0),(0,3),则线段AB长为________.
11.如图,线段OB,OC,OA的长度分别是1,2,3,且OC平分∠AOB,若将A点表示为(3,30°),B点表示为(1,120°),则C点可表示为________.
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-21.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-21.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-21.tif" \* MERGEFORMATINET
12.已知点P(a+3,2a+4)在y轴上,则点P的坐标为________.
13.在平面直角坐标系中,点A在第一象限,点B在x轴的正半轴上,∠AOB=60°,OA=8.点A的坐标是________.
14.在平面直角坐标系中,对于平面内任意一点(x,y),若规定以下两种变换:
①f(x,y)=(x+2,y);②g(x,y)=(-x,-y).
例如按照以上变换有f(1,1)=(3,1);g(f(1,1))=g(3,1)=(-3,-1).
则f(g(2,5))=________.
15.一只小虫在小方格组成的网格线上爬行,它的起始位置是点A(2,2),先爬到点B(2,4),再爬到点C(5,4),最后爬到点D(5,6),则小虫共爬了________个单位.
16.如图,在平面直角坐标系中,一颗棋子从点P(0,-2)处开始依次关于点A(-1,-1),B(1,2),C(2,1)作循环对称跳动,即第1次跳到点P关于点A的对称点M处,第2次跳到点M关于点B的对称点N处,第3次再跳到点N关于点C的对称点Q处……如此下去,则经过第2 020次跳动后,棋子落点的坐标为________.
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\DDXX240.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\DDXX240.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\DDXX240.tif" \* MERGEFORMATINET
三、解答题(17题8分,其余每题9分,共44分)
17.根据如图所示的标示,填一填,标一标,以学校为观测点.
(1)图书馆在学校的______________的方向上,距离学校________m;
(2)游泳池在学校的______________的方向上,距离学校________m;
(3)广场在学校的______________的方向上,距离学校________m;
(4)儿童乐园在学校的南偏东45°的方向上,距离学校3 800 m,请你标出儿童乐园的位置.
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\DDXX241.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\DDXX241.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\DDXX241.tif" \* MERGEFORMATINET
18.在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上(小正方形的顶点称为格点),请解答下列问题:
(1)作出△ABC关于y轴对称的△A1B1C1,点A1与A、B1与B、C1与C对应,并回答下列两个问题:
①写出点C1的坐标;
②已知点P是线段AA1上任意一点,用恰当的方式表示点P的坐标.
(2)若△ABC经过平移后得到△A2B2C2,A的对应点A2的坐标为(-1,-1),写出点B的对应点B2的坐标.
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ443.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ443.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ443.tif" \* MERGEFORMATINET
19.若点M(3a-9,1-a)是平面直角坐标系中第三象限的整数点(横、纵坐标都为整数).
(1)求a的值;
(2)求点M向右平移3个单位得到的点M1的坐标.
20.在平面直角坐标系中,点A关于x轴对称的点的坐标为(x+2y-3,y-x+2),点A关于y轴对称的点的坐标为(2y+2x+1,2x-y+2),求x,y的值.
21.在如图所示的平面直角坐标系中,已知A(0,a),B(b,0),C(3,c)三点,若a,b,c满足关系式:|a-2|+(b-3)2+=0.
(1)求a,b,c的值;
(2)求四边形AOBC的面积;
(3)是否存在点P,使△AOP的面积为四边形AOBC的面积的2倍?若存在,求出点P的坐标,若不存在,请说明理由.
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-22.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-22.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-22.tif" \* MERGEFORMATINET
答案
一、1.C 2.B 3.A 4.B 5.A
6.A 点拨:∵点P(a,1)关于y轴的对称点为Q(2,b),∴a=-2,b=1,则a+b=-2+1=-1.
7.B
8.A
二、9.2 点拨:∵点(a,b)到x轴的距离为|b|,∴点P(1,-2)到x轴的距离为2.
10.5 点拨:∵点A,B的坐标分别为(4,0),(0,3),
∴BO=3,AO=4,∴AB==5.
11.(2,75°)
12.(0,-2) 点拨:∵点P(a+3,2a+4)在y轴上,
∴a+3=0,解得a=-3,∴2a+4=-2,则点P的坐标为(0,-2).
13.(4,4 )
14.(0,-5) 点拨: f(g(2,5))=f(-2,-5)=(-2+2,-5)=(0,-5).
15.7 点拨:从点A(2,2)爬到点B(2,4),爬了4-2=2(个)单位,再爬到点C(5,4),爬了5-2=3(个)单位,最后爬到点D(5,6),爬了6-4=2(个)单位,所以小虫一共爬了2+3+2=7(个)单位.
16.(-2,0) 点拨:连接PA并延长到M,使AM=PA,所以M的坐标是(-2,0);连接MB并延长到N,使BN=MB,所以N的坐标是(4,4);连接NC并延长到Q,使CQ=NC,发现Q与P点重合,即棋子跳动3次后又回到点P处.因为2 020÷3=673……1,所以经过第2 020次跳动后,棋子落在点M处,故答案为(-2,0).
三、17.解:(1)北偏西74°;5 200
(2)北偏东42°;2 500
(3)南偏西60°;3 800
(4)儿童乐园的位置如图所示.
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\DDXX325.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\DDXX325.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\DDXX325.tif" \* MERGEFORMATINET
18.解:(1)如图所示.
①点C1的坐标为(-3,2);
②点P的坐标为(x,4)(-2≤x≤2).
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ643.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ643.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ643.tif" \* MERGEFORMATINET
(2)点B2的坐标为(-2,-4).
19.解:(1)∵点M(3a-9,1-a)是第三象限的整数点,
∴3a-9<0,1-a<0,∴1<a<3.
∵点M的横、纵坐标都为整数,∴a=2.
(2)当a=2时,3a-9=-3,1-a=-1,
∴点M的坐标是(-3,-1).
则点M向右平移3个单位得到的点M1的坐标为(0,-1).
20.解:∵点A关于x轴对称的点的坐标为(x+2y-3,y-x+2),
∴A点坐标为(x+2y-3,-y+x-2).
∵点A关于y轴对称的点的坐标为(2y+2x+1,2x-y+2),
∴A点坐标为(-2y-2x-1,2x-y+2),
∴解得
21.解:(1)∵|a-2|+(b-3)2+=0,
∴a-2=0,b-3=0,c-4=0,
∴a=2,b=3,c=4.
(2)由(1)知A(0,2),O(0,0),B(3,0),C(3,4),
∴四边形AOBC为直角梯形,且OA=2,BC=4,OB=3,
∴四边形AOBC的面积=×(OA+BC)·OB=×(2+4)×3=9.
(3)存在.∵△AOP的面积为四边形AOBC的面积的2倍,
∴△AOP的面积=×2×|x|=2×9,
∴|x|=18,∴x=±18.
∴点P的坐标为(18,-9)或(-18,9).
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
