2021-2022学年湘教版数学八年级下册期末测模拟试卷(word版、含解析)
文档属性
| 名称 | 2021-2022学年湘教版数学八年级下册期末测模拟试卷(word版、含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 202.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-14 00:00:00 | ||
图片预览

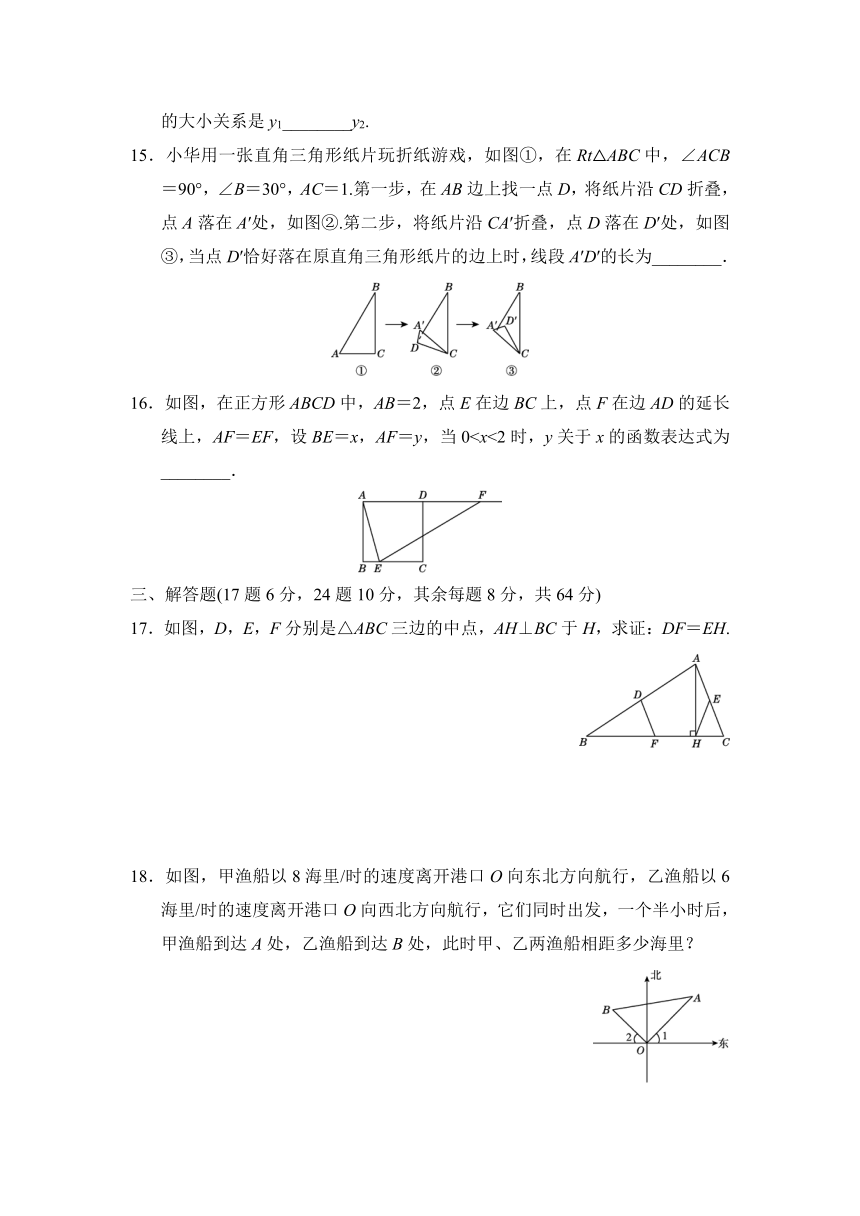

文档简介
第二学期期末测试卷
一、选择题(每题3分,共24分)
1.下列四个图案既是轴对称图形又是中心对称图形的是( )
INCLUDEPICTURE"19X8XJ455.tif" INCLUDEPICTURE "E:\\22春\\8数XJ\\19X8XJ455.tif" \* MERGEFORMATINET INCLUDEPICTURE "E:\\22春\\8数XJ\\19X8XJ455.tif" \* MERGEFORMATINET
2.函数y=的自变量x的取值范围是( )
A.x>2 B.x<2 C.x≥2 D.x≤2
3.某校有500名学生参加外语口语考试,考试成绩在70~85分之间的有120人,则这个分数段的频率是( )
A.0.2 B.0.12 C.0.24 D.0.25
4.如图,PD⊥AB,PE⊥AC,垂足分别为D,E,且PD=PE,则△APD与△APE全等的直接理由是( )
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-33.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-33.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-33.tif" \* MERGEFORMATINET
A.SAS B.AAS C.SSS D.HL
5.如图是一次函数y=kx+b的图象,则k,b的取值范围是( )
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ456.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ456.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ456.tif" \* MERGEFORMATINET
A.k>0,b<0 B.k<0,b>0 C.k<0,b<0 D.k>0,b>0
6.在平面直角坐标系中,已知平行四边形ABCD的三个顶点坐标分别是A(m,n),B(2,-1),C(-m,-n),则关于点D的说法正确的是( )
甲:点D在第一象限;乙:点D与点A关于原点对称;
丙:点D 的坐标是(-2,1);丁:点D与原点的距离是.
A.甲、乙 B.乙、丙 C.甲、丁 D.丙、丁
7.已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当∠A=60°时,它是菱形
B.当AC⊥BD时,它是菱形
C.当AC=BD时,它是矩形
D.当AB=BC,AC=BD时,它是正方形
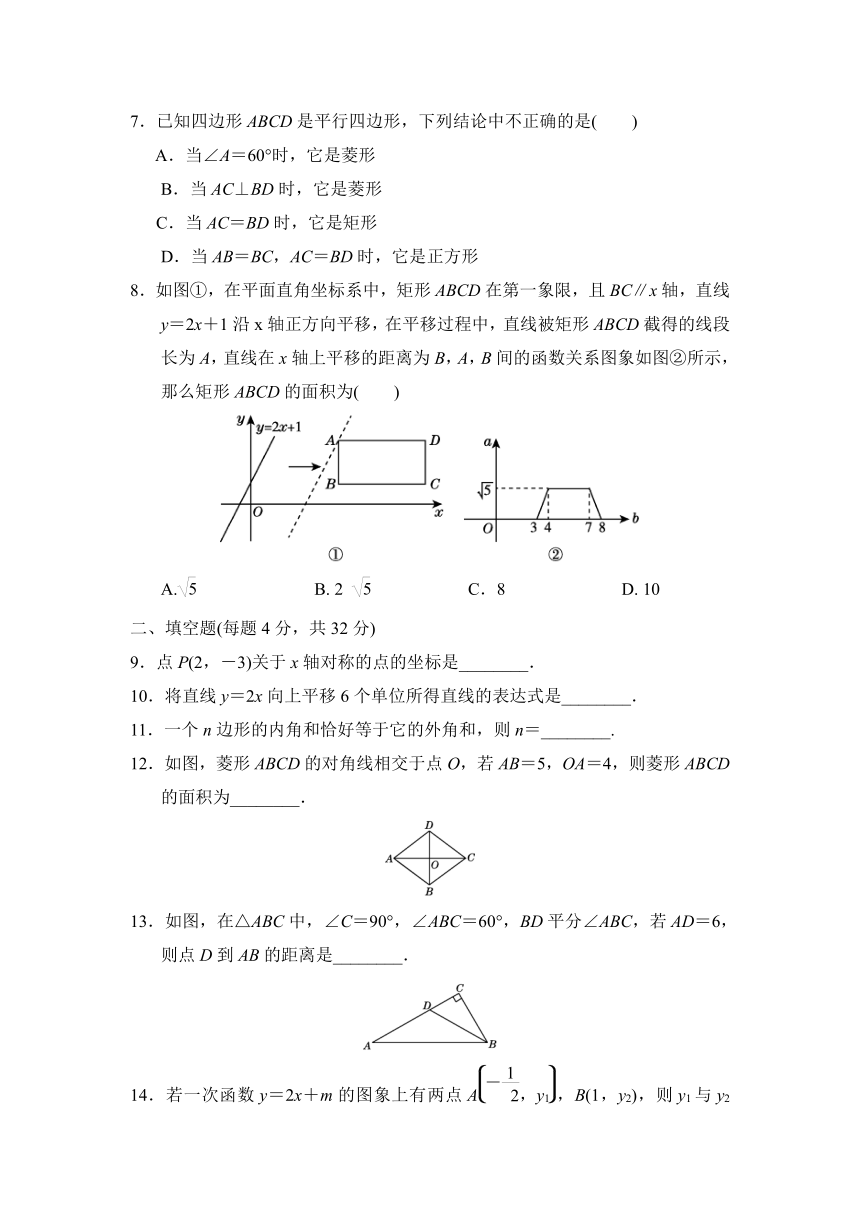
8.如图①,在平面直角坐标系中,矩形ABCD在第一象限,且BC∥x轴,直线y=2x+1沿x轴正方向平移,在平移过程中,直线被矩形ABCD截得的线段长为A,直线在x轴上平移的距离为B,A,B间的函数关系图象如图②所示,那么矩形ABCD的面积为( )
INCLUDEPICTURE"image211.tif" INCLUDEPICTURE "E:\\22春\\8数XJ\\image211.tif" \* MERGEFORMATINET INCLUDEPICTURE "E:\\22春\\8数XJ\\image211.tif" \* MERGEFORMATINET
A. B. 2 C.8 D. 10
二、填空题(每题4分,共32分)
9.点P(2,-3)关于x轴对称的点的坐标是________.
10.将直线y=2x向上平移6个单位所得直线的表达式是________.
11.一个n边形的内角和恰好等于它的外角和,则n=________.
12.如图,菱形ABCD的对角线相交于点O,若AB=5,OA=4,则菱形ABCD的面积为________.
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-35.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-35.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-35.tif" \* MERGEFORMATINET
13.如图,在△ABC中,∠C=90°,∠ABC=60°,BD平分∠ABC,若AD=6,则点D到AB的距离是________.
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-36.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-36.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-36.tif" \* MERGEFORMATINET
14.若一次函数y=2x+m的图象上有两点A,B(1,y2),则y1与y2的大小关系是y1________y2.
15.小华用一张直角三角形纸片玩折纸游戏,如图①,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=1.第一步,在AB边上找一点D,将纸片沿CD折叠,点A落在A′处,如图②.第二步,将纸片沿CA′折叠,点D落在D′处,如图③,当点D′恰好落在原直角三角形纸片的边上时,线段A′D′的长为________.
INCLUDEPICTURE"image212.tif" INCLUDEPICTURE "E:\\22春\\8数XJ\\image212.tif" \* MERGEFORMATINET INCLUDEPICTURE "E:\\22春\\8数XJ\\image212.tif" \* MERGEFORMATINET
16.如图,在正方形ABCD中,AB=2,点E在边BC上,点F在边AD的延长线上,AF=EF,设BE=x,AF=y,当0INCLUDEPICTURE"image213.tif" INCLUDEPICTURE "E:\\22春\\8数XJ\\image213.tif" \* MERGEFORMATINET INCLUDEPICTURE "E:\\22春\\8数XJ\\image213.tif" \* MERGEFORMATINET
三、解答题(17题6分,24题10分,其余每题8分,共64分)
17.如图,D,E,F分别是△ABC三边的中点,AH⊥BC于H,求证:DF=EH.
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-38.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-38.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-38.tif" \* MERGEFORMATINET
18.如图,甲渔船以8海里/时的速度离开港口O向东北方向航行,乙渔船以6海里/时的速度离开港口O向西北方向航行,它们同时出发,一个半小时后,甲渔船到达A处,乙渔船到达B处,此时甲、乙两渔船相距多少海里?
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ463.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ463.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ463.tif" \* MERGEFORMATINET
19.如图,E,F分别是平行四边形ABCD的对角线BD上的点,且BE=DF.
求证:∠DAF=∠BCE.
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ464.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ464.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ464.tif" \* MERGEFORMATINET
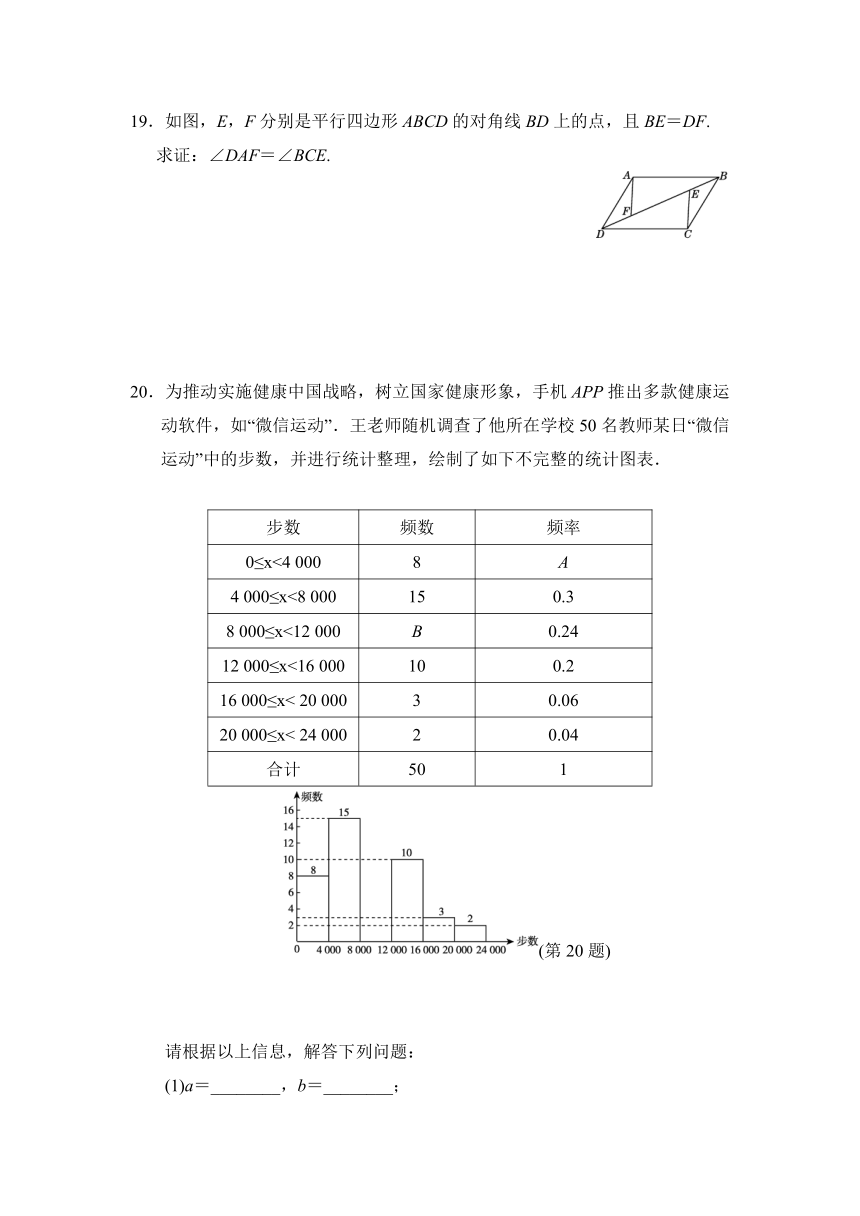
20.为推动实施健康中国战略,树立国家健康形象,手机APP推出多款健康运动软件,如“微信运动”.王老师随机调查了他所在学校50名教师某日“微信运动”中的步数,并进行统计整理,绘制了如下不完整的统计图表.
步数 频数 频率
0≤x<4 000 8 A
4 000≤x<8 000 15 0.3
8 000≤x<12 000 B 0.24
12 000≤x<16 000 10 0.2
16 000≤x< 20 000 3 0.06
20 000≤x< 24 000 2 0.04
合计 50 1
INCLUDEPICTURE"image214.tif" INCLUDEPICTURE "E:\\22春\\8数XJ\\image214.tif" \* MERGEFORMATINET INCLUDEPICTURE "E:\\22春\\8数XJ\\image214.tif" \* MERGEFORMATINET (第20题)
请根据以上信息,解答下列问题:
(1)a=________,b=________;
(2)补全频数分布直方图.
21.已知A(8,0)及在第一象限内的动点P(x,y),且x+y=10,设△OPA的面积为S.
(1)求S关于x的函数表达式;
(2)求x的取值范围;
(3)求S=12时,P点的坐标;
(4)画出函数S的图象.
22.为更新果树品种,某果园计划新购进A,B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种果树苗的单价为7元/棵,购买B种果树苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ467.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ467.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ467.tif" \* MERGEFORMATINET
(1)求y与x的函数关系式;
(2)若在购买计划中,B种果树苗的数量不超过35棵,但不少于A种果树苗的数量,请设计购买方案,使总费用最低,并求出最低总费用.
23.如图,矩形ABCD中,AB=2,BC=5,E,P分别在AD,BC上,且DE=BP=1.
(1)判断△BEC的形状,并说明理由;
(2)判断四边形EFPH是什么特殊四边形,并证明你的判断.
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-39.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-39.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-39.tif" \* MERGEFORMATINET
24.如图,直线l1的表达式为y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.
(1)求点D的坐标;
(2)求直线l2的表达式;
(3)求△ADC的面积;
(4)在直线l2上存在一点P,使得△ADP的面积是△ADC面积的2倍,请求出点P的坐标.
INCLUDEPICTURE"J1-40.tif" INCLUDEPICTURE "E:\\22春\\8数XJ\\J1-40.tif" \* MERGEFORMATINET INCLUDEPICTURE "E:\\22春\\8数XJ\\J1-40.tif" \* MERGEFORMATINET
答案
一、1.B 点拨:A只是中心对称图形;B既是轴对称图形又是中心对称图形;C只是轴对称图形;D既不是中心对称图形也不是轴对称图形.
2.C 点拨:依题意被开方数为非负数,即x-2≥0,∴x≥2.
3.C 4.D
5.D 点拨:∵一次函数y=kx+b的图象过第一、二、三象限,∴k>0.∵图象与y轴的交点在y轴的正半轴上,∴b>0.
6.D 点拨:由平行四边形的中心对称性知点D与点B关于原点对称,且点D在第二象限,坐标为(-2,1),由勾股定理知点D到原点的距离为.故丙、丁正确.
7.A 点拨:对角线互相垂直的平行四边形是菱形,故选项B正确;对角线相等的平行四边形是矩形,故选项C正确;一组邻边相等的平行四边形是菱形,对角线相等的菱形是正方形,故选项D正确,因而选A.
8.C 点拨:如图,过点B,D分别作直线y=2x+1的平行线,交AD,BC于点E,F.根据题图②平移的距离b在4至7时线段a的长度不变,可知BF=7-4=3,
根据题图②易知AE=CF=1,∴BC=BF+FC=3+1=4.
由题图②知线段a的最大值为,即BE=,
在Rt△ABE中,根据勾股定理得AB===2,∴矩形ABCD的面积为AB×BC=2×4=8.
INCLUDEPICTURE"答案+38.tif" INCLUDEPICTURE "E:\\22春\\8数XJ\\答案+38.tif" \* MERGEFORMATINET INCLUDEPICTURE "E:\\22春\\8数XJ\\答案+38.tif" \* MERGEFORMATINET
二、9.(2,3)
10.y=2x+6
11.4
12.24
13.3 点拨:过点D作DE⊥AB于E.∵∠C=90°,∠ABC=60°,BD平分∠ABC,∴∠CBD=∠DBA=∠A=30°,∴AD=BD=6,∴DE=3.
14.< 点拨:∵一次函数y=2x+m中k=2>0,∴y随x的增大而增大.又-<1,∴y1<y2.
15. 或2- 点拨:当D′落在AB边上时,如图①.
设DD′交A′C于点E,由折叠知∠EA′D=∠A=60°,AD=A′D=A′D′,DD′⊥A′E,A′C=AC.
∵∠ACB=90°,∠B=30°,AC=1,∴AB=2,BC=.
设AD=x,则在Rt△A′ED中,易得A′E=x.
在Rt△ECB中,EC=BC=.
∵A′C=AC,∴x+=1,解得x=2-,∴A′D′=2-.
INCLUDEPICTURE"答案+39.tif" INCLUDEPICTURE "E:\\22春\\8数XJ\\答案+39.tif" \* MERGEFORMATINET INCLUDEPICTURE "E:\\22春\\8数XJ\\答案+39.tif" \* MERGEFORMATINET
16.y= 点拨:过点E作EH⊥AF于点H,如图所示.
INCLUDEPICTURE"答案+41.tif" INCLUDEPICTURE "E:\\22春\\8数XJ\\答案+41.tif" \* MERGEFORMATINET INCLUDEPICTURE "E:\\22春\\8数XJ\\答案+41.tif" \* MERGEFORMATINET (第16题)
∵四边形ABCD是正方形,
∴∠BAD=∠B=90°,
∴四边形ABEH是矩形.
∵AB=2,BE=x,
∴EH=AB=2,AH=BE=x.
∵AF=EF,AF=y,
∴HF=y-x,EF=y.
在Rt△EHF中,由勾股定理可得(y-x)2+4=y2,
化简得y=,
∴当0三、17.证明:∵D,E,F分别是△ABC三边的中点,AH⊥BC,
∴DF是△ABC的中位线,HE是Rt△AHC斜边上的中线,
∴DF=AC,HE=AC,∴DF=EH.
18.解:由题意可得:BO=1.5×6=9(海里),AO=1.5×8=12(海里),
∵∠1=∠2=45°,∴∠AOB=90°.
在Rt△AOB中,AB==15海里.
答:此时甲、乙两渔船相距15海里.
19.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,∴∠ADB=∠CBD.
又DF=BE,∴△ADF≌△CBE,∴∠DAF=∠BCE.
20.解:(1)0.16;12
(2)如图所示.
INCLUDEPICTURE"答案+42.tif" INCLUDEPICTURE "E:\\22春\\8数XJ\\答案+42.tif" \* MERGEFORMATINET INCLUDEPICTURE "E:\\22春\\8数XJ\\答案+42.tif" \* MERGEFORMATINET
21.解:(1)∵x+y=10,∴y=10-x,∴S=8(10-x)÷2=40-4x.
(2)0<x<10.
(3)令S=12,则12=40-4x,解得x=7,∴y=10-7=3,
∴当S=12时,P点的坐标为(7,3).
(4)函数S的图象如图所示.
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\D1-6.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\D1-6.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\D1-6.tif" \* MERGEFORMATINET
22.解:(1)当0≤x≤20时,设y与x的函数关系式为y=kx+b,把(0,0),(20,160)代入y=kx+b中,得解得此时y与x的函数关系式为y=8x;
当x>20时,设y与x的函数关系式为y=k′x+b′,把(20,160),(40,288)代入y=k′x+b′中,得解得此时y与x的函数关系式为y=6.4x+32.
综上可知,y与x的函数关系式为y=
(2)∵B种果树苗的数量不超过35棵,但不少于A种果树苗的数量,
∴
∴22.5≤x≤35.
设总费用为W元,则W=6.4x+32+7(45-x)=-0.6x+347.
∵-0.6<0,∴W随x的增大而减小,
∴当x=35,即购买A种果树苗10棵,B种果树苗35棵时,总费用最低,最低总费用为-0.6×35+347=326(元).
23.解:(1)△BEC是直角三角形.理由如下:
∵四边形ABCD是矩形,
∴∠ADC=∠BAD=90°,AD=BC=5,AB=CD=2.
∵DE=1,∴AE=4.
由勾股定理得CE===,
BE===2 ,
∴CE2+BE2=5+20=25,
∵BC2=52=25,∴BE2+CE2=BC2,∴△BEC是直角三角形.
(2)四边形EFPH为矩形,证明如下:
∵四边形ABCD是矩形,∴AD=BC,AD∥BC.
∵DE=BP,∴四边形DEBP是平行四边形,∴BE∥DP.
∵AD=BC,AD∥BC,DE=BP,∴AE=CP,
∴四边形AECP是平行四边形,∴AP∥CE,
∴四边形EFPH是平行四边形.
又由(1)知,∠BEC=90°,∴平行四边形EFPH是矩形.
24.解:(1)由y=-3x+3,令y=0,得-3x+3=0,∴x=1,∴D(1,0).
(2)设直线l2的表达式为y=kx+b,由图象知A(4,0),B,
将(4,0),代入表达式y=kx+b,得∴
∴直线l2的表达式为y=x-6.
(3)由解得
∴C(2,-3).易知AD=3,∴S△ADC=×3×|-3|=.
(4)∵△ADP的面积是△ADC面积的2倍,
即AD·|yP|=AD·|yC|×2,
∴yP=±6.
当yP=6时,令x-6=6,解得x=8,
∴P1(8,6).
当yP=-6时,令x-6=-6,解得x=0,
∴P2(0,-6).
综上所述,点P的坐标为(8,6)或(0,-6).
一、选择题(每题3分,共24分)
1.下列四个图案既是轴对称图形又是中心对称图形的是( )
INCLUDEPICTURE"19X8XJ455.tif" INCLUDEPICTURE "E:\\22春\\8数XJ\\19X8XJ455.tif" \* MERGEFORMATINET INCLUDEPICTURE "E:\\22春\\8数XJ\\19X8XJ455.tif" \* MERGEFORMATINET
2.函数y=的自变量x的取值范围是( )
A.x>2 B.x<2 C.x≥2 D.x≤2
3.某校有500名学生参加外语口语考试,考试成绩在70~85分之间的有120人,则这个分数段的频率是( )
A.0.2 B.0.12 C.0.24 D.0.25
4.如图,PD⊥AB,PE⊥AC,垂足分别为D,E,且PD=PE,则△APD与△APE全等的直接理由是( )
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-33.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-33.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-33.tif" \* MERGEFORMATINET
A.SAS B.AAS C.SSS D.HL
5.如图是一次函数y=kx+b的图象,则k,b的取值范围是( )
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ456.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ456.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ456.tif" \* MERGEFORMATINET
A.k>0,b<0 B.k<0,b>0 C.k<0,b<0 D.k>0,b>0
6.在平面直角坐标系中,已知平行四边形ABCD的三个顶点坐标分别是A(m,n),B(2,-1),C(-m,-n),则关于点D的说法正确的是( )
甲:点D在第一象限;乙:点D与点A关于原点对称;
丙:点D 的坐标是(-2,1);丁:点D与原点的距离是.
A.甲、乙 B.乙、丙 C.甲、丁 D.丙、丁
7.已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当∠A=60°时,它是菱形
B.当AC⊥BD时,它是菱形
C.当AC=BD时,它是矩形
D.当AB=BC,AC=BD时,它是正方形
8.如图①,在平面直角坐标系中,矩形ABCD在第一象限,且BC∥x轴,直线y=2x+1沿x轴正方向平移,在平移过程中,直线被矩形ABCD截得的线段长为A,直线在x轴上平移的距离为B,A,B间的函数关系图象如图②所示,那么矩形ABCD的面积为( )
INCLUDEPICTURE"image211.tif" INCLUDEPICTURE "E:\\22春\\8数XJ\\image211.tif" \* MERGEFORMATINET INCLUDEPICTURE "E:\\22春\\8数XJ\\image211.tif" \* MERGEFORMATINET
A. B. 2 C.8 D. 10
二、填空题(每题4分,共32分)
9.点P(2,-3)关于x轴对称的点的坐标是________.
10.将直线y=2x向上平移6个单位所得直线的表达式是________.
11.一个n边形的内角和恰好等于它的外角和,则n=________.
12.如图,菱形ABCD的对角线相交于点O,若AB=5,OA=4,则菱形ABCD的面积为________.
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-35.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-35.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-35.tif" \* MERGEFORMATINET
13.如图,在△ABC中,∠C=90°,∠ABC=60°,BD平分∠ABC,若AD=6,则点D到AB的距离是________.
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-36.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-36.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-36.tif" \* MERGEFORMATINET
14.若一次函数y=2x+m的图象上有两点A,B(1,y2),则y1与y2的大小关系是y1________y2.
15.小华用一张直角三角形纸片玩折纸游戏,如图①,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=1.第一步,在AB边上找一点D,将纸片沿CD折叠,点A落在A′处,如图②.第二步,将纸片沿CA′折叠,点D落在D′处,如图③,当点D′恰好落在原直角三角形纸片的边上时,线段A′D′的长为________.
INCLUDEPICTURE"image212.tif" INCLUDEPICTURE "E:\\22春\\8数XJ\\image212.tif" \* MERGEFORMATINET INCLUDEPICTURE "E:\\22春\\8数XJ\\image212.tif" \* MERGEFORMATINET
16.如图,在正方形ABCD中,AB=2,点E在边BC上,点F在边AD的延长线上,AF=EF,设BE=x,AF=y,当0
三、解答题(17题6分,24题10分,其余每题8分,共64分)
17.如图,D,E,F分别是△ABC三边的中点,AH⊥BC于H,求证:DF=EH.
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-38.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-38.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-38.tif" \* MERGEFORMATINET
18.如图,甲渔船以8海里/时的速度离开港口O向东北方向航行,乙渔船以6海里/时的速度离开港口O向西北方向航行,它们同时出发,一个半小时后,甲渔船到达A处,乙渔船到达B处,此时甲、乙两渔船相距多少海里?
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ463.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ463.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ463.tif" \* MERGEFORMATINET
19.如图,E,F分别是平行四边形ABCD的对角线BD上的点,且BE=DF.
求证:∠DAF=∠BCE.
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ464.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ464.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ464.tif" \* MERGEFORMATINET
20.为推动实施健康中国战略,树立国家健康形象,手机APP推出多款健康运动软件,如“微信运动”.王老师随机调查了他所在学校50名教师某日“微信运动”中的步数,并进行统计整理,绘制了如下不完整的统计图表.
步数 频数 频率
0≤x<4 000 8 A
4 000≤x<8 000 15 0.3
8 000≤x<12 000 B 0.24
12 000≤x<16 000 10 0.2
16 000≤x< 20 000 3 0.06
20 000≤x< 24 000 2 0.04
合计 50 1
INCLUDEPICTURE"image214.tif" INCLUDEPICTURE "E:\\22春\\8数XJ\\image214.tif" \* MERGEFORMATINET INCLUDEPICTURE "E:\\22春\\8数XJ\\image214.tif" \* MERGEFORMATINET (第20题)
请根据以上信息,解答下列问题:
(1)a=________,b=________;
(2)补全频数分布直方图.
21.已知A(8,0)及在第一象限内的动点P(x,y),且x+y=10,设△OPA的面积为S.
(1)求S关于x的函数表达式;
(2)求x的取值范围;
(3)求S=12时,P点的坐标;
(4)画出函数S的图象.
22.为更新果树品种,某果园计划新购进A,B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种果树苗的单价为7元/棵,购买B种果树苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ467.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ467.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\19X8XJ467.tif" \* MERGEFORMATINET
(1)求y与x的函数关系式;
(2)若在购买计划中,B种果树苗的数量不超过35棵,但不少于A种果树苗的数量,请设计购买方案,使总费用最低,并求出最低总费用.
23.如图,矩形ABCD中,AB=2,BC=5,E,P分别在AD,BC上,且DE=BP=1.
(1)判断△BEC的形状,并说明理由;
(2)判断四边形EFPH是什么特殊四边形,并证明你的判断.
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-39.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-39.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\J1-39.tif" \* MERGEFORMATINET
24.如图,直线l1的表达式为y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.
(1)求点D的坐标;
(2)求直线l2的表达式;
(3)求△ADC的面积;
(4)在直线l2上存在一点P,使得△ADP的面积是△ADC面积的2倍,请求出点P的坐标.
INCLUDEPICTURE"J1-40.tif" INCLUDEPICTURE "E:\\22春\\8数XJ\\J1-40.tif" \* MERGEFORMATINET INCLUDEPICTURE "E:\\22春\\8数XJ\\J1-40.tif" \* MERGEFORMATINET
答案
一、1.B 点拨:A只是中心对称图形;B既是轴对称图形又是中心对称图形;C只是轴对称图形;D既不是中心对称图形也不是轴对称图形.
2.C 点拨:依题意被开方数为非负数,即x-2≥0,∴x≥2.
3.C 4.D
5.D 点拨:∵一次函数y=kx+b的图象过第一、二、三象限,∴k>0.∵图象与y轴的交点在y轴的正半轴上,∴b>0.
6.D 点拨:由平行四边形的中心对称性知点D与点B关于原点对称,且点D在第二象限,坐标为(-2,1),由勾股定理知点D到原点的距离为.故丙、丁正确.
7.A 点拨:对角线互相垂直的平行四边形是菱形,故选项B正确;对角线相等的平行四边形是矩形,故选项C正确;一组邻边相等的平行四边形是菱形,对角线相等的菱形是正方形,故选项D正确,因而选A.
8.C 点拨:如图,过点B,D分别作直线y=2x+1的平行线,交AD,BC于点E,F.根据题图②平移的距离b在4至7时线段a的长度不变,可知BF=7-4=3,
根据题图②易知AE=CF=1,∴BC=BF+FC=3+1=4.
由题图②知线段a的最大值为,即BE=,
在Rt△ABE中,根据勾股定理得AB===2,∴矩形ABCD的面积为AB×BC=2×4=8.
INCLUDEPICTURE"答案+38.tif" INCLUDEPICTURE "E:\\22春\\8数XJ\\答案+38.tif" \* MERGEFORMATINET INCLUDEPICTURE "E:\\22春\\8数XJ\\答案+38.tif" \* MERGEFORMATINET
二、9.(2,3)
10.y=2x+6
11.4
12.24
13.3 点拨:过点D作DE⊥AB于E.∵∠C=90°,∠ABC=60°,BD平分∠ABC,∴∠CBD=∠DBA=∠A=30°,∴AD=BD=6,∴DE=3.
14.< 点拨:∵一次函数y=2x+m中k=2>0,∴y随x的增大而增大.又-<1,∴y1<y2.
15. 或2- 点拨:当D′落在AB边上时,如图①.
设DD′交A′C于点E,由折叠知∠EA′D=∠A=60°,AD=A′D=A′D′,DD′⊥A′E,A′C=AC.
∵∠ACB=90°,∠B=30°,AC=1,∴AB=2,BC=.
设AD=x,则在Rt△A′ED中,易得A′E=x.
在Rt△ECB中,EC=BC=.
∵A′C=AC,∴x+=1,解得x=2-,∴A′D′=2-.
INCLUDEPICTURE"答案+39.tif" INCLUDEPICTURE "E:\\22春\\8数XJ\\答案+39.tif" \* MERGEFORMATINET INCLUDEPICTURE "E:\\22春\\8数XJ\\答案+39.tif" \* MERGEFORMATINET
16.y= 点拨:过点E作EH⊥AF于点H,如图所示.
INCLUDEPICTURE"答案+41.tif" INCLUDEPICTURE "E:\\22春\\8数XJ\\答案+41.tif" \* MERGEFORMATINET INCLUDEPICTURE "E:\\22春\\8数XJ\\答案+41.tif" \* MERGEFORMATINET (第16题)
∵四边形ABCD是正方形,
∴∠BAD=∠B=90°,
∴四边形ABEH是矩形.
∵AB=2,BE=x,
∴EH=AB=2,AH=BE=x.
∵AF=EF,AF=y,
∴HF=y-x,EF=y.
在Rt△EHF中,由勾股定理可得(y-x)2+4=y2,
化简得y=,
∴当0
∴DF是△ABC的中位线,HE是Rt△AHC斜边上的中线,
∴DF=AC,HE=AC,∴DF=EH.
18.解:由题意可得:BO=1.5×6=9(海里),AO=1.5×8=12(海里),
∵∠1=∠2=45°,∴∠AOB=90°.
在Rt△AOB中,AB==15海里.
答:此时甲、乙两渔船相距15海里.
19.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,∴∠ADB=∠CBD.
又DF=BE,∴△ADF≌△CBE,∴∠DAF=∠BCE.
20.解:(1)0.16;12
(2)如图所示.
INCLUDEPICTURE"答案+42.tif" INCLUDEPICTURE "E:\\22春\\8数XJ\\答案+42.tif" \* MERGEFORMATINET INCLUDEPICTURE "E:\\22春\\8数XJ\\答案+42.tif" \* MERGEFORMATINET
21.解:(1)∵x+y=10,∴y=10-x,∴S=8(10-x)÷2=40-4x.
(2)0<x<10.
(3)令S=12,则12=40-4x,解得x=7,∴y=10-7=3,
∴当S=12时,P点的坐标为(7,3).
(4)函数S的图象如图所示.
INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\D1-6.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\D1-6.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\21春初中\\数学\\8XJ\\word\\D1-6.tif" \* MERGEFORMATINET
22.解:(1)当0≤x≤20时,设y与x的函数关系式为y=kx+b,把(0,0),(20,160)代入y=kx+b中,得解得此时y与x的函数关系式为y=8x;
当x>20时,设y与x的函数关系式为y=k′x+b′,把(20,160),(40,288)代入y=k′x+b′中,得解得此时y与x的函数关系式为y=6.4x+32.
综上可知,y与x的函数关系式为y=
(2)∵B种果树苗的数量不超过35棵,但不少于A种果树苗的数量,
∴
∴22.5≤x≤35.
设总费用为W元,则W=6.4x+32+7(45-x)=-0.6x+347.
∵-0.6<0,∴W随x的增大而减小,
∴当x=35,即购买A种果树苗10棵,B种果树苗35棵时,总费用最低,最低总费用为-0.6×35+347=326(元).
23.解:(1)△BEC是直角三角形.理由如下:
∵四边形ABCD是矩形,
∴∠ADC=∠BAD=90°,AD=BC=5,AB=CD=2.
∵DE=1,∴AE=4.
由勾股定理得CE===,
BE===2 ,
∴CE2+BE2=5+20=25,
∵BC2=52=25,∴BE2+CE2=BC2,∴△BEC是直角三角形.
(2)四边形EFPH为矩形,证明如下:
∵四边形ABCD是矩形,∴AD=BC,AD∥BC.
∵DE=BP,∴四边形DEBP是平行四边形,∴BE∥DP.
∵AD=BC,AD∥BC,DE=BP,∴AE=CP,
∴四边形AECP是平行四边形,∴AP∥CE,
∴四边形EFPH是平行四边形.
又由(1)知,∠BEC=90°,∴平行四边形EFPH是矩形.
24.解:(1)由y=-3x+3,令y=0,得-3x+3=0,∴x=1,∴D(1,0).
(2)设直线l2的表达式为y=kx+b,由图象知A(4,0),B,
将(4,0),代入表达式y=kx+b,得∴
∴直线l2的表达式为y=x-6.
(3)由解得
∴C(2,-3).易知AD=3,∴S△ADC=×3×|-3|=.
(4)∵△ADP的面积是△ADC面积的2倍,
即AD·|yP|=AD·|yC|×2,
∴yP=±6.
当yP=6时,令x-6=6,解得x=8,
∴P1(8,6).
当yP=-6时,令x-6=-6,解得x=0,
∴P2(0,-6).
综上所述,点P的坐标为(8,6)或(0,-6).
同课章节目录
