2021-2022学年人教A版(2019)数学选择性必修第一册1.1.1空间向量及其线性运算 课件(共22张PPT)
文档属性
| 名称 | 2021-2022学年人教A版(2019)数学选择性必修第一册1.1.1空间向量及其线性运算 课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-14 20:03:23 | ||
图片预览






文档简介
(共22张PPT)
1.1.1空间向量及其线性运算
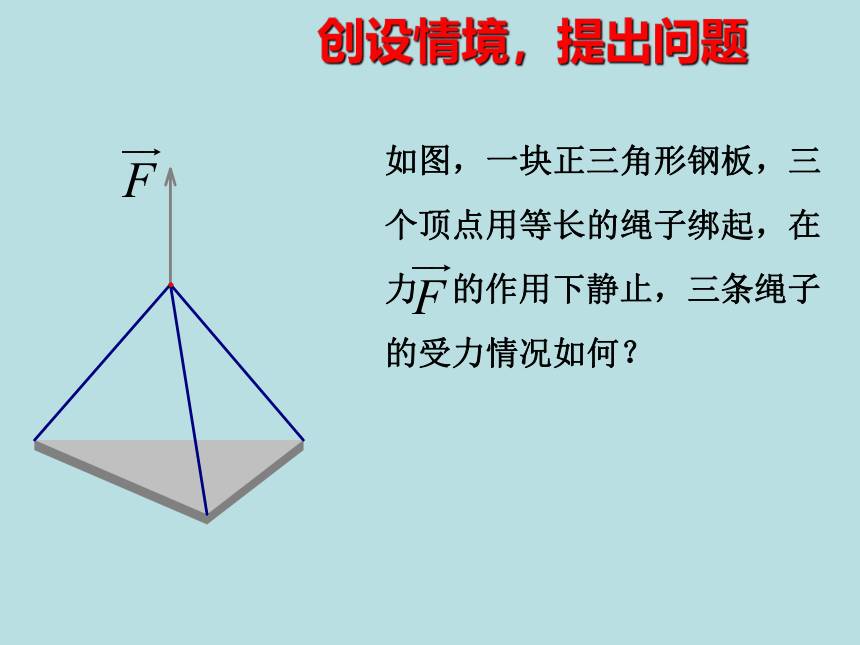
创设情境,提出问题
如图,一块正三角形钢板,三个顶点用等长的绳子绑起,在力 的作用下静止,三条绳子的受力情况如何?
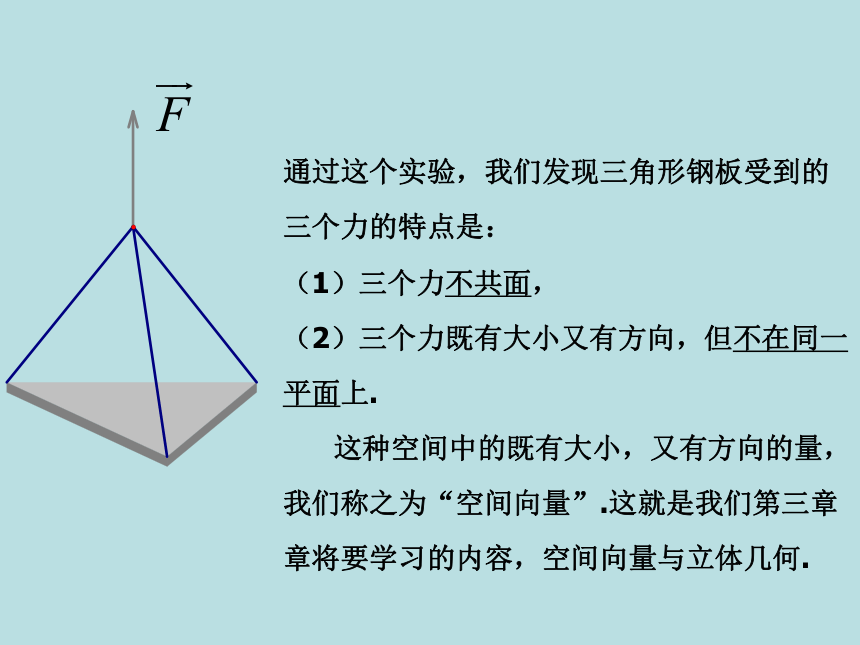
通过这个实验,我们发现三角形钢板受到的三个力的特点是:
(1)三个力不共面,
(2)三个力既有大小又有方向,但不在同一平面上.
这种空间中的既有大小,又有方向的量,我们称之为“空间向量”.这就是我们第三章章将要学习的内容,空间向量与立体几何.
我们先看到第三章简介
类比平面向量,空间向量有关概念
平面向量和空间向量没有本质的区别,因此我们可以通过类比平面向量的有关概念,加减运算等知识来学习空间向量。
内容 平面向量 空间向量
概念
画法及其表示
零向量
单位向量
相等向量
相反向量
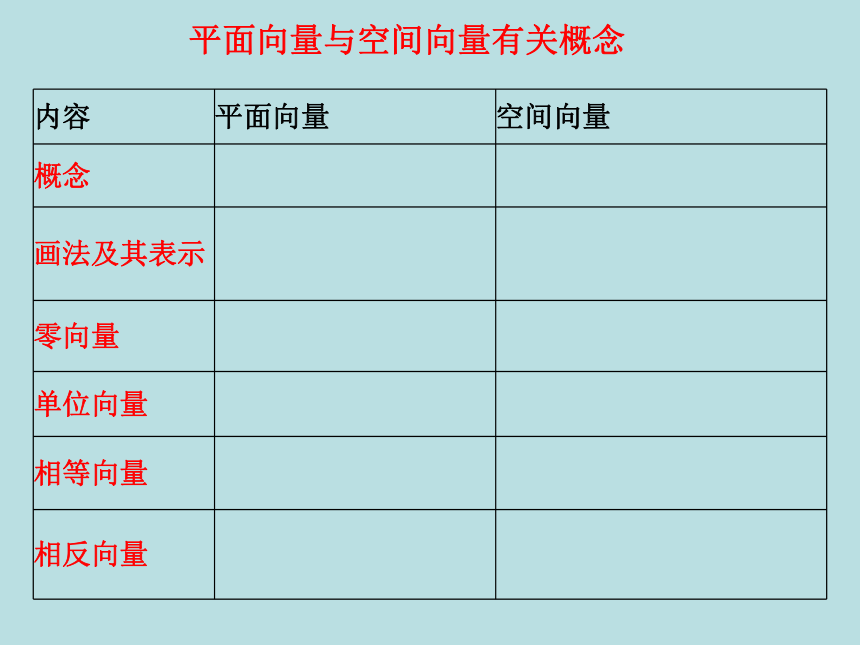
平面向量与空间向量有关概念
内容 平面向量 空间向量
概念
画法及其表示
零向量
单位向量
相等向量
用有向线段画出来,记作:
或
在平面上,既有大小又有方向的量,其大小叫做向量的模
在空间,具有大小和方向的量,其大小叫做向量的模
用有向线段画出来,记作:
或
长度为零的向量叫做零向量,零向量的方向是任意的
长度为零的向量叫做零向量,零向量的方向是任意的
平面中模为1的向量
空间中模为1的向量
平面中方向相同且模相等的两个向量
空间中方向相同且模相等的两个向量
平面向量与空间向量有关概念
相反向量
平面中长度相等而方向相反的向量
空间中长度相等而方向相反的向量
平面向量与空间向量有关概念
② ③ ④
复习平面向量加减运算
1.加法运算
(1)平行四边形法则:
(2)三角形法则:
2.减法运算:
类比的结果是否正确?如何证明?这就是我们这节课的第二个问题:空间向量的加减运算
问题:在平行四边形中 中,由平行四边形法则可知, ,类比平行四边形中的结论,那么在平行六面体 中, 如何表示?
空间向量的加减运算
a
b
a
b
O
A
B
b
结论:空间任意两个向量都可以平移到同一个平面内,所以它们 可用同一平面内的两条有向线段表示.
因此凡是涉及空间任意两个向量的问题,平面向量
中有关结论仍适用于它们.
思考:空间中任意两个向量是否一定能够平移到同一个平面内?
空间向量的加减运算
在空间中,任意两个向量都可以平移到同一个平面内,所以空间向量的加法和减法运算与平面向量相同.
(1)空间向量加法运算:
平行四边形法则:
三角形法则:
注:首尾顺次相接,起点指向终点
三角形法则推广
首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.
空间向量的加减运算
在空间中,任意两个向量都可以平移到同一个平面内,所以空间向量的加法和减法运算与平面向量相同.
(2)空间向量的减法运算:
注:起点相同,差向量为减向量终点指向被减向量的终点
空间向量加法运算律
⑴加法交换律:
⑵加法结合律:
问题:平面向量的加法运算符合交换律和结合律,空间向量是否也符合?
问题:能否借助空间图形说明加法结合律的合理性?
加法结合律
这个过程同时也说明了前面类比结果是正确的
类比的结果是否正确?如何证明?这就是我们这节课的第二个问题:空间向量的加减运算
问题:在平行四边形中 中,由平行四边形法则可知, ,类比平行四边形中的结论,那么在平行六面体 中, 如何表示?
空间向量的加减运算
例2
变式
规律总结:
掌握好向量加减法的三角形法则是解决这类问题的关键,灵活应用相反向量、相等向量及两向量和、差,可使这类题迅速获解.
当堂检测
A
D
C
相等
相反
课堂小结
1.这节课你收获了哪些知识?
2.你是如何获得的?
3.你在获得知识的过程中用到了哪些数学思想方法?
4.你还有哪些疑惑
作业:P86第3题P97第1题(1)(2)
1.1.1空间向量及其线性运算
创设情境,提出问题
如图,一块正三角形钢板,三个顶点用等长的绳子绑起,在力 的作用下静止,三条绳子的受力情况如何?
通过这个实验,我们发现三角形钢板受到的三个力的特点是:
(1)三个力不共面,
(2)三个力既有大小又有方向,但不在同一平面上.
这种空间中的既有大小,又有方向的量,我们称之为“空间向量”.这就是我们第三章章将要学习的内容,空间向量与立体几何.
我们先看到第三章简介
类比平面向量,空间向量有关概念
平面向量和空间向量没有本质的区别,因此我们可以通过类比平面向量的有关概念,加减运算等知识来学习空间向量。
内容 平面向量 空间向量
概念
画法及其表示
零向量
单位向量
相等向量
相反向量
平面向量与空间向量有关概念
内容 平面向量 空间向量
概念
画法及其表示
零向量
单位向量
相等向量
用有向线段画出来,记作:
或
在平面上,既有大小又有方向的量,其大小叫做向量的模
在空间,具有大小和方向的量,其大小叫做向量的模
用有向线段画出来,记作:
或
长度为零的向量叫做零向量,零向量的方向是任意的
长度为零的向量叫做零向量,零向量的方向是任意的
平面中模为1的向量
空间中模为1的向量
平面中方向相同且模相等的两个向量
空间中方向相同且模相等的两个向量
平面向量与空间向量有关概念
相反向量
平面中长度相等而方向相反的向量
空间中长度相等而方向相反的向量
平面向量与空间向量有关概念
② ③ ④
复习平面向量加减运算
1.加法运算
(1)平行四边形法则:
(2)三角形法则:
2.减法运算:
类比的结果是否正确?如何证明?这就是我们这节课的第二个问题:空间向量的加减运算
问题:在平行四边形中 中,由平行四边形法则可知, ,类比平行四边形中的结论,那么在平行六面体 中, 如何表示?
空间向量的加减运算
a
b
a
b
O
A
B
b
结论:空间任意两个向量都可以平移到同一个平面内,所以它们 可用同一平面内的两条有向线段表示.
因此凡是涉及空间任意两个向量的问题,平面向量
中有关结论仍适用于它们.
思考:空间中任意两个向量是否一定能够平移到同一个平面内?
空间向量的加减运算
在空间中,任意两个向量都可以平移到同一个平面内,所以空间向量的加法和减法运算与平面向量相同.
(1)空间向量加法运算:
平行四边形法则:
三角形法则:
注:首尾顺次相接,起点指向终点
三角形法则推广
首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.
空间向量的加减运算
在空间中,任意两个向量都可以平移到同一个平面内,所以空间向量的加法和减法运算与平面向量相同.
(2)空间向量的减法运算:
注:起点相同,差向量为减向量终点指向被减向量的终点
空间向量加法运算律
⑴加法交换律:
⑵加法结合律:
问题:平面向量的加法运算符合交换律和结合律,空间向量是否也符合?
问题:能否借助空间图形说明加法结合律的合理性?
加法结合律
这个过程同时也说明了前面类比结果是正确的
类比的结果是否正确?如何证明?这就是我们这节课的第二个问题:空间向量的加减运算
问题:在平行四边形中 中,由平行四边形法则可知, ,类比平行四边形中的结论,那么在平行六面体 中, 如何表示?
空间向量的加减运算
例2
变式
规律总结:
掌握好向量加减法的三角形法则是解决这类问题的关键,灵活应用相反向量、相等向量及两向量和、差,可使这类题迅速获解.
当堂检测
A
D
C
相等
相反
课堂小结
1.这节课你收获了哪些知识?
2.你是如何获得的?
3.你在获得知识的过程中用到了哪些数学思想方法?
4.你还有哪些疑惑
作业:P86第3题P97第1题(1)(2)
