2021—2022学年人教版数学七年级上册2.1整式多项式 课件(第二课时 35张)
文档属性
| 名称 | 2021—2022学年人教版数学七年级上册2.1整式多项式 课件(第二课时 35张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-14 18:14:46 | ||
图片预览



文档简介
(共35张PPT)
2.1 整式
第2课时 多项式及整式
青藏铁路线上,在格尔木到拉萨之间有一段很长的冻土地段.列车在冻土地段、非冻土地段的行驶速度分别是100 km/h和120 km/h.列车在冻土地段行驶了m小时,在非冻土地段行驶了n小时。请列式表示列车总的行驶了多少千米?
【问题1】
例1.用含字母的式子表示下列数量关系
(1)一条河的水流速度是2.5 km/h,船在静水中的速度是 v km/h,用式子表示船在这条河中顺水行驶和逆水行驶时的速度;
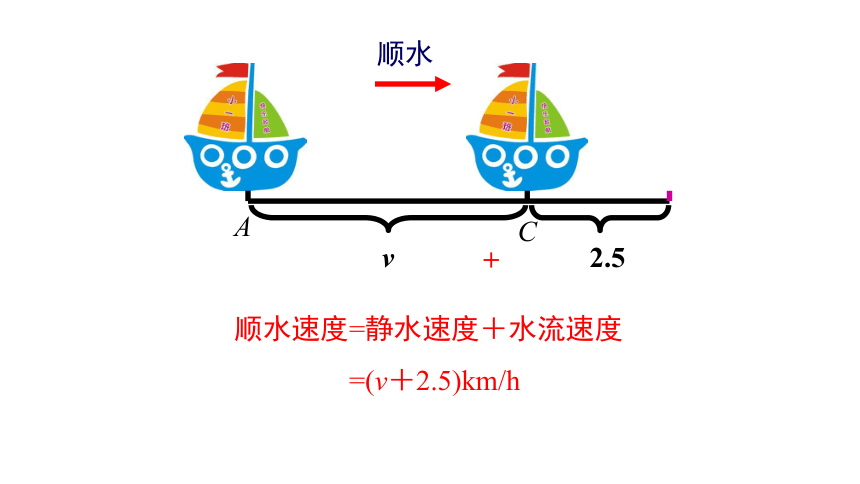
顺水
A
C
v
2.5
+
顺水速度=静水速度+水流速度
=(v+2.5)km/h
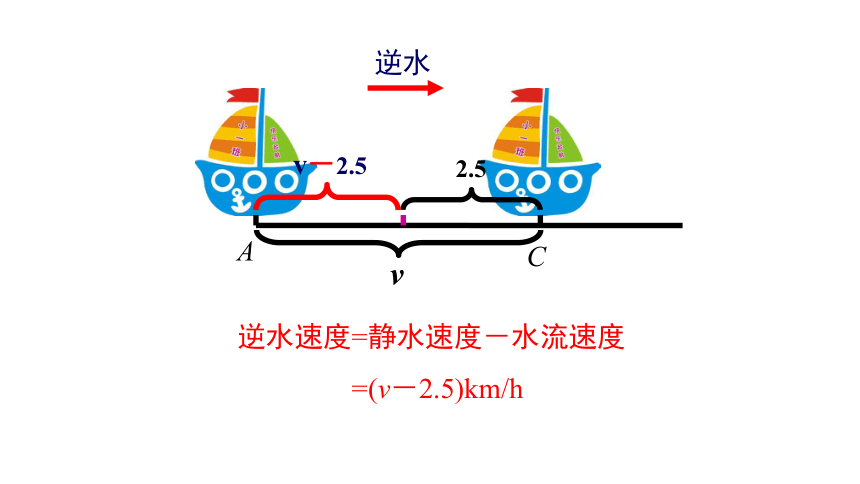
逆水
A
C
v
2.5
v-2.5
逆水速度=静水速度-水流速度
=(v-2.5)km/h
(2)买一个篮球需要x元,买一个排球需要y元,买一个足球需要 z 元,用式子表示买 3个篮球、5个排球、2个足球共需要的钱数;
解:买3个篮球、5个排球、2个足球共需要
元.
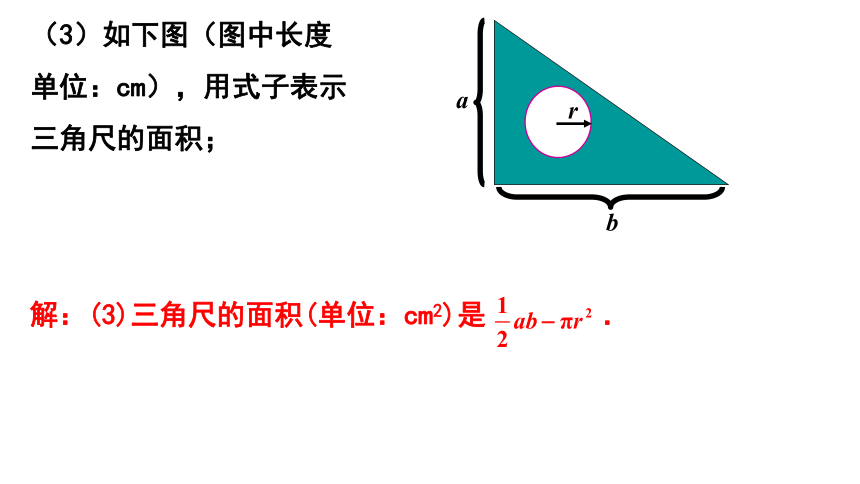
(3)如下图(图中长度单位:cm),用式子表示三角尺的面积;
解:(3)三角尺的面积(单位:cm2)是 .
a
b
r
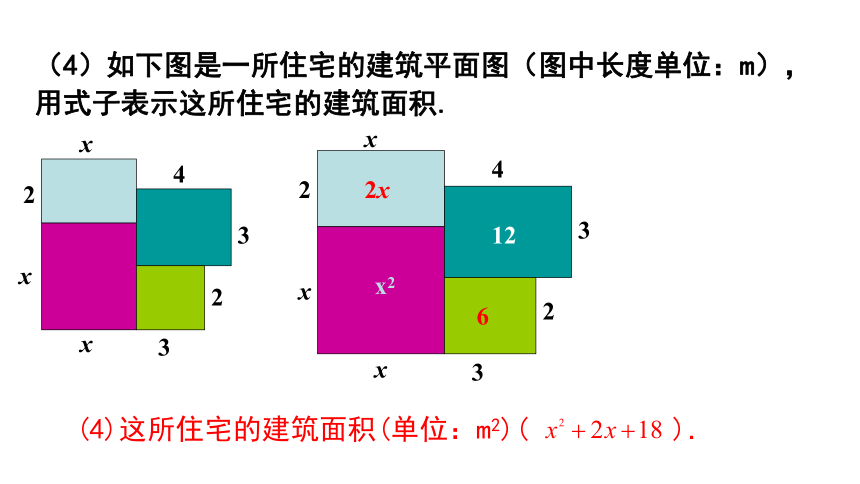
(4)这所住宅的建筑面积(单位:m2)( ).
(4)如下图是一所住宅的建筑平面图(图中长度单位:m),用式子表示这所住宅的建筑面积.
2
x
2x
x
x
x2
3
4
2
3
12
6
3
2
x
x
4
2
3
x
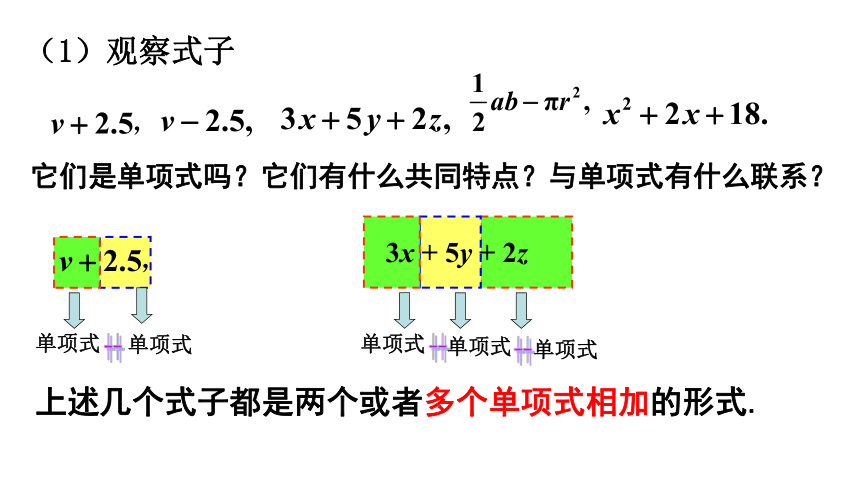
(1)观察式子
它们是单项式吗?它们有什么共同特点?与单项式有什么联系?
上述几个式子都是两个或者多个单项式相加的形式.
单项式
单项式
3x + 5y + 2z
+
单项式
单项式
+
单项式
+
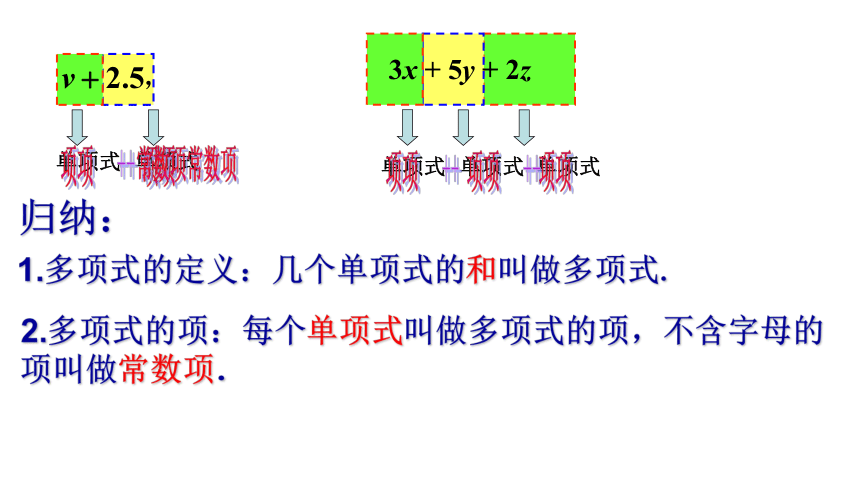
归纳:
1.多项式的定义:几个单项式的和叫做多项式.
2.多项式的项:每个单项式叫做多项式的项,不含字母的项叫做常数项.
单项式
单项式
3x + 5y + 2z
+
项
项
常数项
单项式
单项式
+
项
项
单项式
+
项
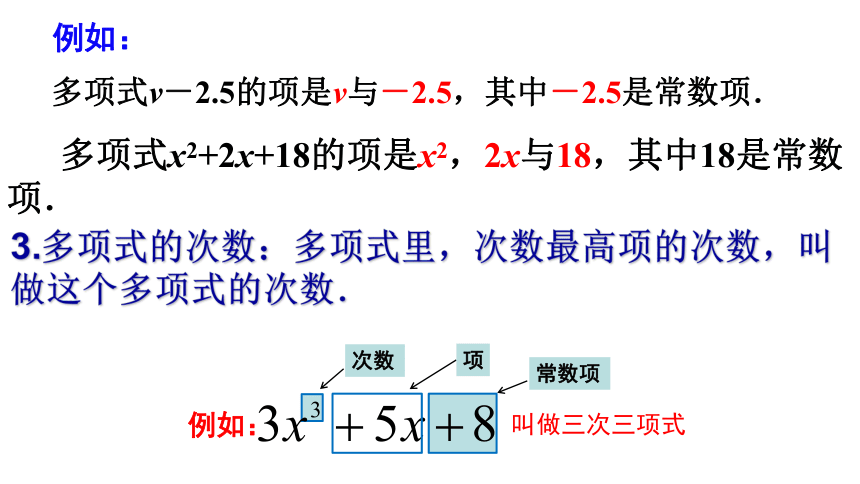
多项式x2+2x+18的项是x2,2x与18,其中18是常数项.
多项式v-2.5的项是v与-2.5,其中-2.5是常数项.
3.多项式的次数:多项式里,次数最高项的次数,叫做这个多项式的次数.
例如:
例如:
常数项
次数
项
叫做三次三项式
,
,
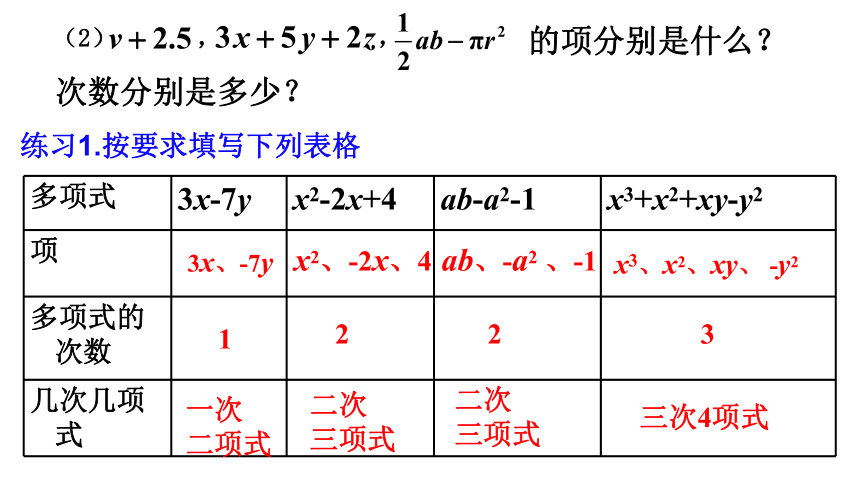
(2)
的项分别是什么?
次数分别是多少?
多项式 3x-7y x2-2x+4 ab-a2-1 x3+x2+xy-y2
项
多项式的次数
几次几项式
练习1.按要求填写下列表格
3x、-7y
x2、-2x、4
ab、-a2 、-1
x3、x2、xy、 -y2
1
2
2
3
一次
二项式
二次
三项式
二次
三项式
三次4项式
5.整式的定义:单项式与多项式统称整式.
例1.下列整式中哪些是单项式?哪些是多项式?是单项式的指出系数和次数,是多项式的指出项和次数:
x
32t3
1
32
1
3
0
6
3
解:是单项式的如下表
1
4
2
是多项式的如下表:
(1)多项式的各项应包括它前面的符号;
(3)要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的;
(4)一个多项式的最高次项可以不唯一。
(2)多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号;
温馨提示:
例2.已知-5xm+104xm+1-4xmy2是关于x、y的六次多项式,求m的值,并写出该多项式.
解:由题意得m+2=6,所以m=4.
归纳总结:解题的关键是弄清多项式次数是多项式中次数最高的项的次数.然后根据题意,列出方程,求出m的值.
分析:该多项式最高次项为-4xmy2,其次数为m+2,故m+2=6.
所以该多项式为-5x4+104x5-4x4y2.
练习2.若关于x的多项式-5x3-mx2+(n-1)x-1不含二次项和一次项,求m、n的值.
分析:多项式不含哪一项,则哪一项的系数为0.
解:由题意得m=0,n-1=0,所以n=1.
m,n当作已知常数看待,属于系数部分
例3 .如图,用式子表示圆环的面积.当 cm, cm 时,求圆环的面积( 取 ).
解:外圆的面积减去内圆的面积就是圆环的面积,所以圆环的面积是 .
当 cm , cm 时,
圆环的面积(单位:cm2)是
1. 多项式 的项有___________,常数项是_______,一次项系数是____________,属于_____次_____项式.
2. 用整式填空,指出单项式的系数、次数以及多项式的项和次数.
(1)某种苹果的售价是每千克x元,用面值是50元的人民币购买6千克,花费_____元,应找回_______元.
(2)图中的阴影部分的面积为____________.
课堂 检测
2r
a
(3)某种商品原价每件b元,第一次降价打八折,第二次降价每件又减10元,第一次降价后的售价是________元,第二次降价后的售价是_________元.
3.三个植树队,第一队植树x棵,第二队植的树比第一队的2倍少25棵,第三队植的树比第一队植树的一半多42棵,则第二队、第三队各植树多少棵?当 x=100时,三队共植树多少棵?
(1)一个旅游团有成人x人、学生y人,那么该旅游团应付多少门票费?
(2)如果该旅游团有37个成人、15个学生,那么他们应付多少门票费?
4.某公园的门票价格是:成人10元/张;学生5元/张.
(1)本节课学了哪些主要内容?
(2)请你举例说明多项式的概念、多项式的项和次数的概念.
(3)请你举例说明整式的概念.
【归纳小结】
归纳:列式就是把实际问题中与数量有关的语句,用含有数、字母和运算符号的式子表示出来,也就是把文字语言转化为符号语言.
①要抓住关键词语,明确它们的意义以及它们之间的关系,如和、差、积、商及大、小、多、少、倍、分、倒数、相反数等;
②理清语句层次明确运算顺序;
③牢记一些概念和公式.
【课堂小结】
(1)本节课学了哪些主要内容?
(2)用字母表示数有什么意义?用含有字母的式子表示数量关系有什么意义
(3)用含有字母的式子表示数量关系时要注意什么?
2.1 整式
第2课时 多项式及整式
青藏铁路线上,在格尔木到拉萨之间有一段很长的冻土地段.列车在冻土地段、非冻土地段的行驶速度分别是100 km/h和120 km/h.列车在冻土地段行驶了m小时,在非冻土地段行驶了n小时。请列式表示列车总的行驶了多少千米?
【问题1】
例1.用含字母的式子表示下列数量关系
(1)一条河的水流速度是2.5 km/h,船在静水中的速度是 v km/h,用式子表示船在这条河中顺水行驶和逆水行驶时的速度;
顺水
A
C
v
2.5
+
顺水速度=静水速度+水流速度
=(v+2.5)km/h
逆水
A
C
v
2.5
v-2.5
逆水速度=静水速度-水流速度
=(v-2.5)km/h
(2)买一个篮球需要x元,买一个排球需要y元,买一个足球需要 z 元,用式子表示买 3个篮球、5个排球、2个足球共需要的钱数;
解:买3个篮球、5个排球、2个足球共需要
元.
(3)如下图(图中长度单位:cm),用式子表示三角尺的面积;
解:(3)三角尺的面积(单位:cm2)是 .
a
b
r
(4)这所住宅的建筑面积(单位:m2)( ).
(4)如下图是一所住宅的建筑平面图(图中长度单位:m),用式子表示这所住宅的建筑面积.
2
x
2x
x
x
x2
3
4
2
3
12
6
3
2
x
x
4
2
3
x
(1)观察式子
它们是单项式吗?它们有什么共同特点?与单项式有什么联系?
上述几个式子都是两个或者多个单项式相加的形式.
单项式
单项式
3x + 5y + 2z
+
单项式
单项式
+
单项式
+
归纳:
1.多项式的定义:几个单项式的和叫做多项式.
2.多项式的项:每个单项式叫做多项式的项,不含字母的项叫做常数项.
单项式
单项式
3x + 5y + 2z
+
项
项
常数项
单项式
单项式
+
项
项
单项式
+
项
多项式x2+2x+18的项是x2,2x与18,其中18是常数项.
多项式v-2.5的项是v与-2.5,其中-2.5是常数项.
3.多项式的次数:多项式里,次数最高项的次数,叫做这个多项式的次数.
例如:
例如:
常数项
次数
项
叫做三次三项式
,
,
(2)
的项分别是什么?
次数分别是多少?
多项式 3x-7y x2-2x+4 ab-a2-1 x3+x2+xy-y2
项
多项式的次数
几次几项式
练习1.按要求填写下列表格
3x、-7y
x2、-2x、4
ab、-a2 、-1
x3、x2、xy、 -y2
1
2
2
3
一次
二项式
二次
三项式
二次
三项式
三次4项式
5.整式的定义:单项式与多项式统称整式.
例1.下列整式中哪些是单项式?哪些是多项式?是单项式的指出系数和次数,是多项式的指出项和次数:
x
32t3
1
32
1
3
0
6
3
解:是单项式的如下表
1
4
2
是多项式的如下表:
(1)多项式的各项应包括它前面的符号;
(3)要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的;
(4)一个多项式的最高次项可以不唯一。
(2)多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号;
温馨提示:
例2.已知-5xm+104xm+1-4xmy2是关于x、y的六次多项式,求m的值,并写出该多项式.
解:由题意得m+2=6,所以m=4.
归纳总结:解题的关键是弄清多项式次数是多项式中次数最高的项的次数.然后根据题意,列出方程,求出m的值.
分析:该多项式最高次项为-4xmy2,其次数为m+2,故m+2=6.
所以该多项式为-5x4+104x5-4x4y2.
练习2.若关于x的多项式-5x3-mx2+(n-1)x-1不含二次项和一次项,求m、n的值.
分析:多项式不含哪一项,则哪一项的系数为0.
解:由题意得m=0,n-1=0,所以n=1.
m,n当作已知常数看待,属于系数部分
例3 .如图,用式子表示圆环的面积.当 cm, cm 时,求圆环的面积( 取 ).
解:外圆的面积减去内圆的面积就是圆环的面积,所以圆环的面积是 .
当 cm , cm 时,
圆环的面积(单位:cm2)是
1. 多项式 的项有___________,常数项是_______,一次项系数是____________,属于_____次_____项式.
2. 用整式填空,指出单项式的系数、次数以及多项式的项和次数.
(1)某种苹果的售价是每千克x元,用面值是50元的人民币购买6千克,花费_____元,应找回_______元.
(2)图中的阴影部分的面积为____________.
课堂 检测
2r
a
(3)某种商品原价每件b元,第一次降价打八折,第二次降价每件又减10元,第一次降价后的售价是________元,第二次降价后的售价是_________元.
3.三个植树队,第一队植树x棵,第二队植的树比第一队的2倍少25棵,第三队植的树比第一队植树的一半多42棵,则第二队、第三队各植树多少棵?当 x=100时,三队共植树多少棵?
(1)一个旅游团有成人x人、学生y人,那么该旅游团应付多少门票费?
(2)如果该旅游团有37个成人、15个学生,那么他们应付多少门票费?
4.某公园的门票价格是:成人10元/张;学生5元/张.
(1)本节课学了哪些主要内容?
(2)请你举例说明多项式的概念、多项式的项和次数的概念.
(3)请你举例说明整式的概念.
【归纳小结】
归纳:列式就是把实际问题中与数量有关的语句,用含有数、字母和运算符号的式子表示出来,也就是把文字语言转化为符号语言.
①要抓住关键词语,明确它们的意义以及它们之间的关系,如和、差、积、商及大、小、多、少、倍、分、倒数、相反数等;
②理清语句层次明确运算顺序;
③牢记一些概念和公式.
【课堂小结】
(1)本节课学了哪些主要内容?
(2)用字母表示数有什么意义?用含有字母的式子表示数量关系有什么意义
(3)用含有字母的式子表示数量关系时要注意什么?
