2021春北师大版九下数学2.5二次函数与一元二次方程导学案(含答案)
文档属性
| 名称 | 2021春北师大版九下数学2.5二次函数与一元二次方程导学案(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 123.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-15 07:19:16 | ||
图片预览



文档简介
2021春北师版九下数学2.5二次函数与一元二次方程导学案
学习目标
1、体会二次函数与一元二次方程之间的联系。
2、理解二次函数图像与x轴交点的个数与一元二次方程的根的个数之间的关系,学会利用二次函数图像求一元二次方程的近似根。
学习策略
结合所学过的二次函数和一元二次方程的知识,理解它们之间的联系;
能利用二次函数图像求一元二次方程的近似根.
学习过程
复习回顾:
1、已知二次函数的图象与x轴的交点坐标是(-1,0),(5,0),且函数的最值是-3.则该抛物线是( ).
A.y=13x2-43x+53 B.y=13x2-43x-53 C.y=-13x2+43x+53 D.y=-13x2-43x+53
2、一元二次方程ax2+bx+c=0,当Δ 时,方程有两个不相等的实数根;当Δ_____时,方程有两个相等的实数根;当Δ 时,方程没有实数根
二.新课学习:
1.自学教材P51-55,回答以下问题
二次函数y=ax2+bx+c的图像与x轴的交点有三种情况: 、 、 。与此对应,一元二次方程ax2+bx+c=0的根也有三种情况: 、 、 。
二次函数y=ax2+bx+c的图像与x轴的交点的 就是一元二次方程ax2+bx+c=0的 。
2、自学课本P51-55思考下列问题:
(1)二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根的关系是什么?
(2)利用二次函数y=ax2+bx+c的图象求一元二次方程ax2+bx+c=0的近似根的一般步骤是什么?
三.尝试应用:
1.当a < 0 时,方程ax2+bx+c=0无实数根,则二次函数y=ax2+bx+c的图像一定在 ( )
A、x轴上方 B、x轴下方 C、y轴右侧 D、y轴左侧
2.关于x的一元二次方程x2+bx+c=0的两根为x1=1,x2=2,那么抛物线y=x2+bx+c的顶点坐标为__________.
3.已知二次函数y=x2+4x+k-1.
(1)若抛物线与x轴有两个不同的交点,求k的取值范围;
(2)若抛物线的顶点在x轴上,求k的值.
自主总结:
(1)二次函数y=ax2+bx+c的图象与x轴的交点的 就是一元二次方程ax2+bx+c=0的根.
(2)二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根的关系:a.与x轴有 个交点,有两个相异的实数根,根的判别式Δ=b2-4ac>0;b.与x轴有1个交点,有 的实数根,根的判别式 ;c.与x轴没有交点,没有实数根,根的判别式 .(3)利用二次函数y=ax2+bx+c的图象求一元二次方程ax2+bx+c=0的近似根的一般步骤:①用 作二次函数y=ax2+bx+c的图象;②观察估计二次函数的图象与x轴的 的横坐标;③确定一元二次方程ax2+bx+c=0的 。
五.达标测试
一、选择题
1.如图所示的抛物线是二次函数y=ax2+bx+c(a≠0)的图象,则下列结论:①abc>0;②b+2a=0;③抛物线与x轴的另一个交点为(4,0);④a+c>b,其中正确的结论有( ).
A.1个 B.2个 C.3个 D.4个
2.抛物线与x轴的交点个数是( )
A.0 B.1 C.2 D.3
3.若二次函数y=ax2﹣2ax+c的图象经过点(﹣1,0),则方程ax2﹣2ax+c=0的解为( )
A.x1=﹣3,x2=﹣1 B.x1=1,x2=3
C.x1=﹣1,x2=3 D.x1=﹣3,x2=1
二、填空题
4.抛物线y=x2-2x+k与x轴没有交点,则k的取值范围是_____.
5.如图,是二次函数y=ax2+bx-c的部分图象,由图象可知关于x的一元二次方程ax2+bx=c的两个根可能是________.(精确到0.1)
6.抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3, 0)和(-2 ,0)之间,其部分图象如图,则以下结论:①b2-4ac<0 ;②a+b+c<0;③c-a=2;④方程ax2+bx+c+2=0有两个相等的实数根,其中正确结论的个数为______个.
三、解答题
7. 已知抛物线.
(1)若抛物线与y轴交点的坐标为(0,1),求抛物线与x轴交点的坐标;
(2)证明:无论p为何值,抛物线与x轴必有交点.
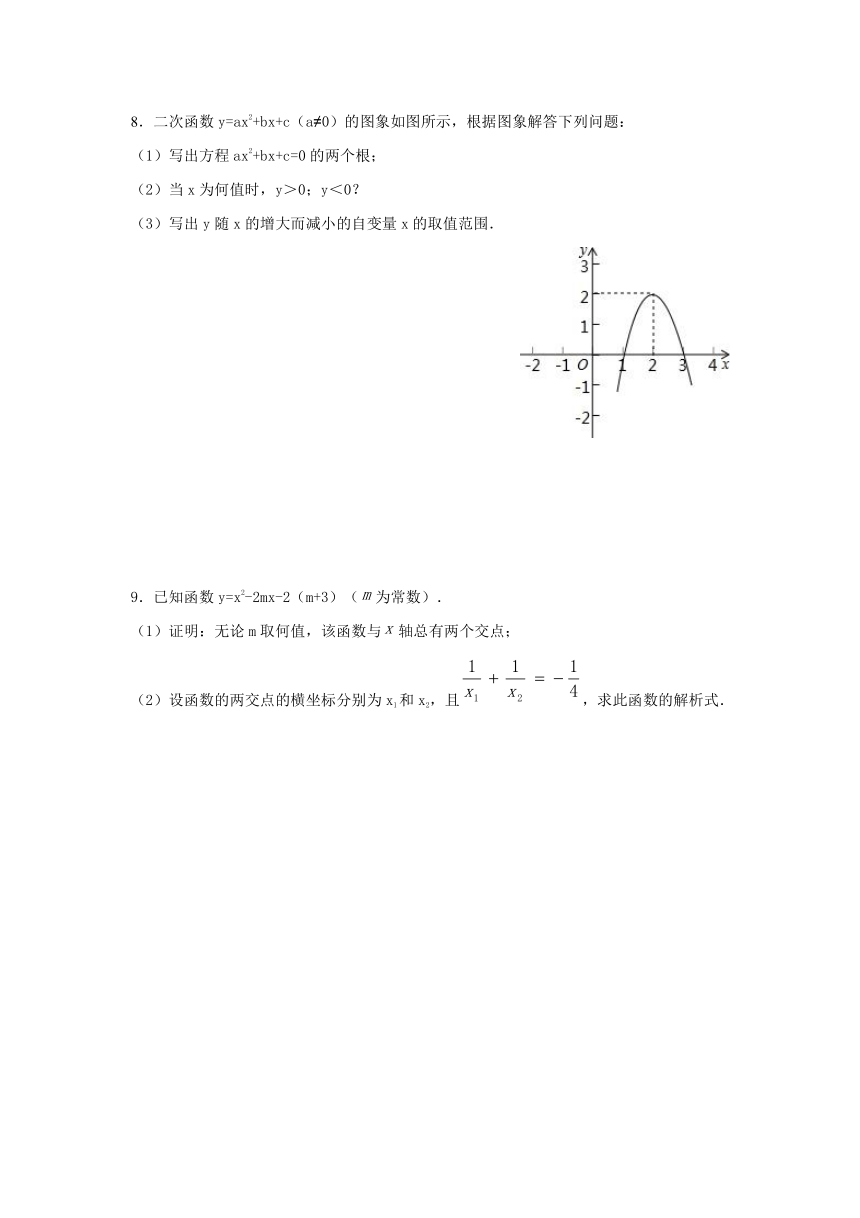
8.二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
(1)写出方程ax2+bx+c=0的两个根;
(2)当x为何值时,y>0;y<0?
(3)写出y随x的增大而减小的自变量x的取值范围.
9.已知函数y=x2-2mx-2(m+3)(为常数).
(1)证明:无论m取何值,该函数与轴总有两个交点;
(2)设函数的两交点的横坐标分别为x1和x2,且,求此函数的解析式.
10.如图,二次函数y1=ax2+bx+3的图象与x轴相交于点A(﹣3,0)、B(1,0),交y轴于点C,C、D是二次函数图象上的一对对称点,一次函数y2=mx+n的图象经过B、D两点.
(1)求二次函数的解析式及点D的坐标;
(2)根据图象写出y2>y1时,x的取值范围.
达标测试答案
一、选择题
1.【解析】试题分析:∵抛物线开口向上,∴a>0,∵抛物线的对称轴为直线x==1,∴b=﹣2a<0,所以②正确;∵抛物线与y轴的交点在x轴下方,∴c<0,∴abc>0,所以①正确;∵点(﹣2,0)关于直线x=1的对称点的坐标为(4,0),∴抛物线与x轴的另一个交点坐标为(4,0),所以③正确;∵x=﹣1时,y<0,
即a﹣b+c<0,∴a+c<b,所以④错误.
故选:C.
考点:抛物线与x轴的交点;二次函数图象与系数的关系.
2.【解析】试题分析:根据题意得△=,所以抛物线与x轴只有一个交点.故选B.
考点:抛物线与x轴的交点.
3.【解析】试题分析:根据题意可得:二次函数的对称轴为直线x=1,则函数与x轴的交点坐标为(-1,0)和(3,0),则方程的解为x=-1或x=3.
考点:二次函数的性质
二、填空题
4.【解析】由题意得
,
考点:二次函数的性质
5.【解析】试题解析:依题意得二次函数y=ax2+bx+c的部分图象的对称轴为x=2,
而对称轴左侧图象与x轴交点与原点的距离,约为0.8,
∴x1=0.8;
又∵对称轴为x=2,
则,
∴x2=2×2-0.8=3.2.
考点:二次函数的性质
6.【解析】试题解析:∵抛物线与x轴有两个交点,
∴b2-4ac>0,所以①错误;
∵顶点为D(-1,2),
∴抛物线的对称轴为直线x=-1,
∵抛物线与x轴的一个交点A在点(-3,0)和(-2,0)之间,
∴抛物线与x轴的另一个交点在点(0,0)和(1,0)之间,
∴当x=1时,y<0,
∴a+b+c<0,所以②正确;
∵抛物线的顶点为D(-1,2),
∴a-b+c=2,
∵抛物线的对称轴为直线x=-=-1,
∴b=2a,
∴a-2a+c=2,即c-a=2,所以③正确;
∵当x=-1时,二次函数有最大值为2,
即只有x=-1时,ax2+bx+c=2,
∴方程ax2+bx+c -2=0有两个相等的实数根,所以④正确.
故正确结论的个数有3个.
考点:二次函数的图象与系数的关系
三、解答题
7.【解析】试题分析:(1)、将x=0,y=1代入函数解析式求出p的值,然后令y=0得出方程的解,从而求出抛物线与x轴的交点坐标;(2)、利用一元二次方程根的判别式得出答案.
试题解析:(1)、对于抛物线 将x=0,y=1代入得:,即,
所以抛物线解析式为 令y=0,得到, 解得:,
则抛物线与x轴交点的坐标为(,0)与(2,0)
(2)、对于一元二次方程
∵△=p2﹣4(﹣)=p2﹣2p+1=(p﹣1)2≥0, ∴无论p为何值,抛物线与x轴必有交点
考点:二次函数的性质
8.【解析】试题分析:(1)、方程的解就是函数图象与x轴的交点;(2)、根据图形可以进行判定;(3)、在对称轴的右边,y随x的增大而减小.
试题解析:(1)、由图形可得:x1=1,x2=3;
(2)、结合图形可得:1<x<3时y>0;x<1或x>3时y<0;
(3)、根据图形可得当x≥2时,y随x的增大而减小.
考点:二次函数图象的性质.
9.【解析】试题分析:(1)证明△=b2-4ac>0即可;(2)利用根与系数的关系得到x1+x2=2m,x1x2=-2(m+3)代入,解方程得出m=1即可.
试题解析:(1)令y=0,得△=(-2m)2-4[-2(m+3)]=4(m+1)2+20>0
∴无论m取何值,方程x2-2mx-2(m+3)=0总有两个不相等的实数根.
即无论m取何值,该函数与轴总有两个交点.
(2)依题意有x1+x2=2m,x1x2=-2(m+3)
由,解得m=1.∴函数的解析式为y=x2-2x-8.
考点:二次函数与一元二次方程.
10.【解析】试题分析:(1)将A、B的坐标代入抛物线的解析式中即可求得待定系数的值,进而可根据抛物线的对称轴求出D点的坐标;
(2)联立两函数的解析式,即可求得B、D的坐标,进而可判断出y2>y1时x的取值范围.
试题解析:(1)二次函数y1=ax2+bx+3的图象经过点A(﹣3,0),B(1,0);
∴,解得;
∴二次函数图象的解析式为y1=﹣x2﹣2x+3;
∴点D的坐标为(﹣2,3);
(2)y2>y1时,x的取值范围是x<﹣2或x>1.
考点:二次函数综合题;待定系数法求二次函数解析式.
学习目标
1、体会二次函数与一元二次方程之间的联系。
2、理解二次函数图像与x轴交点的个数与一元二次方程的根的个数之间的关系,学会利用二次函数图像求一元二次方程的近似根。
学习策略
结合所学过的二次函数和一元二次方程的知识,理解它们之间的联系;
能利用二次函数图像求一元二次方程的近似根.
学习过程
复习回顾:
1、已知二次函数的图象与x轴的交点坐标是(-1,0),(5,0),且函数的最值是-3.则该抛物线是( ).
A.y=13x2-43x+53 B.y=13x2-43x-53 C.y=-13x2+43x+53 D.y=-13x2-43x+53
2、一元二次方程ax2+bx+c=0,当Δ 时,方程有两个不相等的实数根;当Δ_____时,方程有两个相等的实数根;当Δ 时,方程没有实数根
二.新课学习:
1.自学教材P51-55,回答以下问题
二次函数y=ax2+bx+c的图像与x轴的交点有三种情况: 、 、 。与此对应,一元二次方程ax2+bx+c=0的根也有三种情况: 、 、 。
二次函数y=ax2+bx+c的图像与x轴的交点的 就是一元二次方程ax2+bx+c=0的 。
2、自学课本P51-55思考下列问题:
(1)二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根的关系是什么?
(2)利用二次函数y=ax2+bx+c的图象求一元二次方程ax2+bx+c=0的近似根的一般步骤是什么?
三.尝试应用:
1.当a < 0 时,方程ax2+bx+c=0无实数根,则二次函数y=ax2+bx+c的图像一定在 ( )
A、x轴上方 B、x轴下方 C、y轴右侧 D、y轴左侧
2.关于x的一元二次方程x2+bx+c=0的两根为x1=1,x2=2,那么抛物线y=x2+bx+c的顶点坐标为__________.
3.已知二次函数y=x2+4x+k-1.
(1)若抛物线与x轴有两个不同的交点,求k的取值范围;
(2)若抛物线的顶点在x轴上,求k的值.
自主总结:
(1)二次函数y=ax2+bx+c的图象与x轴的交点的 就是一元二次方程ax2+bx+c=0的根.
(2)二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根的关系:a.与x轴有 个交点,有两个相异的实数根,根的判别式Δ=b2-4ac>0;b.与x轴有1个交点,有 的实数根,根的判别式 ;c.与x轴没有交点,没有实数根,根的判别式 .(3)利用二次函数y=ax2+bx+c的图象求一元二次方程ax2+bx+c=0的近似根的一般步骤:①用 作二次函数y=ax2+bx+c的图象;②观察估计二次函数的图象与x轴的 的横坐标;③确定一元二次方程ax2+bx+c=0的 。
五.达标测试
一、选择题
1.如图所示的抛物线是二次函数y=ax2+bx+c(a≠0)的图象,则下列结论:①abc>0;②b+2a=0;③抛物线与x轴的另一个交点为(4,0);④a+c>b,其中正确的结论有( ).
A.1个 B.2个 C.3个 D.4个
2.抛物线与x轴的交点个数是( )
A.0 B.1 C.2 D.3
3.若二次函数y=ax2﹣2ax+c的图象经过点(﹣1,0),则方程ax2﹣2ax+c=0的解为( )
A.x1=﹣3,x2=﹣1 B.x1=1,x2=3
C.x1=﹣1,x2=3 D.x1=﹣3,x2=1
二、填空题
4.抛物线y=x2-2x+k与x轴没有交点,则k的取值范围是_____.
5.如图,是二次函数y=ax2+bx-c的部分图象,由图象可知关于x的一元二次方程ax2+bx=c的两个根可能是________.(精确到0.1)
6.抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3, 0)和(-2 ,0)之间,其部分图象如图,则以下结论:①b2-4ac<0 ;②a+b+c<0;③c-a=2;④方程ax2+bx+c+2=0有两个相等的实数根,其中正确结论的个数为______个.
三、解答题
7. 已知抛物线.
(1)若抛物线与y轴交点的坐标为(0,1),求抛物线与x轴交点的坐标;
(2)证明:无论p为何值,抛物线与x轴必有交点.
8.二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
(1)写出方程ax2+bx+c=0的两个根;
(2)当x为何值时,y>0;y<0?
(3)写出y随x的增大而减小的自变量x的取值范围.
9.已知函数y=x2-2mx-2(m+3)(为常数).
(1)证明:无论m取何值,该函数与轴总有两个交点;
(2)设函数的两交点的横坐标分别为x1和x2,且,求此函数的解析式.
10.如图,二次函数y1=ax2+bx+3的图象与x轴相交于点A(﹣3,0)、B(1,0),交y轴于点C,C、D是二次函数图象上的一对对称点,一次函数y2=mx+n的图象经过B、D两点.
(1)求二次函数的解析式及点D的坐标;
(2)根据图象写出y2>y1时,x的取值范围.
达标测试答案
一、选择题
1.【解析】试题分析:∵抛物线开口向上,∴a>0,∵抛物线的对称轴为直线x==1,∴b=﹣2a<0,所以②正确;∵抛物线与y轴的交点在x轴下方,∴c<0,∴abc>0,所以①正确;∵点(﹣2,0)关于直线x=1的对称点的坐标为(4,0),∴抛物线与x轴的另一个交点坐标为(4,0),所以③正确;∵x=﹣1时,y<0,
即a﹣b+c<0,∴a+c<b,所以④错误.
故选:C.
考点:抛物线与x轴的交点;二次函数图象与系数的关系.
2.【解析】试题分析:根据题意得△=,所以抛物线与x轴只有一个交点.故选B.
考点:抛物线与x轴的交点.
3.【解析】试题分析:根据题意可得:二次函数的对称轴为直线x=1,则函数与x轴的交点坐标为(-1,0)和(3,0),则方程的解为x=-1或x=3.
考点:二次函数的性质
二、填空题
4.【解析】由题意得
,
考点:二次函数的性质
5.【解析】试题解析:依题意得二次函数y=ax2+bx+c的部分图象的对称轴为x=2,
而对称轴左侧图象与x轴交点与原点的距离,约为0.8,
∴x1=0.8;
又∵对称轴为x=2,
则,
∴x2=2×2-0.8=3.2.
考点:二次函数的性质
6.【解析】试题解析:∵抛物线与x轴有两个交点,
∴b2-4ac>0,所以①错误;
∵顶点为D(-1,2),
∴抛物线的对称轴为直线x=-1,
∵抛物线与x轴的一个交点A在点(-3,0)和(-2,0)之间,
∴抛物线与x轴的另一个交点在点(0,0)和(1,0)之间,
∴当x=1时,y<0,
∴a+b+c<0,所以②正确;
∵抛物线的顶点为D(-1,2),
∴a-b+c=2,
∵抛物线的对称轴为直线x=-=-1,
∴b=2a,
∴a-2a+c=2,即c-a=2,所以③正确;
∵当x=-1时,二次函数有最大值为2,
即只有x=-1时,ax2+bx+c=2,
∴方程ax2+bx+c -2=0有两个相等的实数根,所以④正确.
故正确结论的个数有3个.
考点:二次函数的图象与系数的关系
三、解答题
7.【解析】试题分析:(1)、将x=0,y=1代入函数解析式求出p的值,然后令y=0得出方程的解,从而求出抛物线与x轴的交点坐标;(2)、利用一元二次方程根的判别式得出答案.
试题解析:(1)、对于抛物线 将x=0,y=1代入得:,即,
所以抛物线解析式为 令y=0,得到, 解得:,
则抛物线与x轴交点的坐标为(,0)与(2,0)
(2)、对于一元二次方程
∵△=p2﹣4(﹣)=p2﹣2p+1=(p﹣1)2≥0, ∴无论p为何值,抛物线与x轴必有交点
考点:二次函数的性质
8.【解析】试题分析:(1)、方程的解就是函数图象与x轴的交点;(2)、根据图形可以进行判定;(3)、在对称轴的右边,y随x的增大而减小.
试题解析:(1)、由图形可得:x1=1,x2=3;
(2)、结合图形可得:1<x<3时y>0;x<1或x>3时y<0;
(3)、根据图形可得当x≥2时,y随x的增大而减小.
考点:二次函数图象的性质.
9.【解析】试题分析:(1)证明△=b2-4ac>0即可;(2)利用根与系数的关系得到x1+x2=2m,x1x2=-2(m+3)代入,解方程得出m=1即可.
试题解析:(1)令y=0,得△=(-2m)2-4[-2(m+3)]=4(m+1)2+20>0
∴无论m取何值,方程x2-2mx-2(m+3)=0总有两个不相等的实数根.
即无论m取何值,该函数与轴总有两个交点.
(2)依题意有x1+x2=2m,x1x2=-2(m+3)
由,解得m=1.∴函数的解析式为y=x2-2x-8.
考点:二次函数与一元二次方程.
10.【解析】试题分析:(1)将A、B的坐标代入抛物线的解析式中即可求得待定系数的值,进而可根据抛物线的对称轴求出D点的坐标;
(2)联立两函数的解析式,即可求得B、D的坐标,进而可判断出y2>y1时x的取值范围.
试题解析:(1)二次函数y1=ax2+bx+3的图象经过点A(﹣3,0),B(1,0);
∴,解得;
∴二次函数图象的解析式为y1=﹣x2﹣2x+3;
∴点D的坐标为(﹣2,3);
(2)y2>y1时,x的取值范围是x<﹣2或x>1.
考点:二次函数综合题;待定系数法求二次函数解析式.
