2021春北师版九下数学3.4.2圆周角和圆心角的关系导学案(有答案)
文档属性
| 名称 | 2021春北师版九下数学3.4.2圆周角和圆心角的关系导学案(有答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 374.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-15 07:31:05 | ||
图片预览


文档简介
2021春北师版九下数学3.4.2圆周角和圆心角的关系导学案
学习目标
1.掌握圆周角定理的2个推论的内容.
2.会熟练运用推论解决问题.
学习重点:圆周角定理的几个推论的应用.
学习难点:理解几个推论的“题设”和“结论”
学法指导:在30分钟内独立完成预习学案,相信自己,锻炼自己!通过预习,把自己的疑惑记录下来,向小组同学请教,如果还是存在疑惑,课堂上认真听同学或老师讲解,把不懂的问题及时解决。
一、预习案
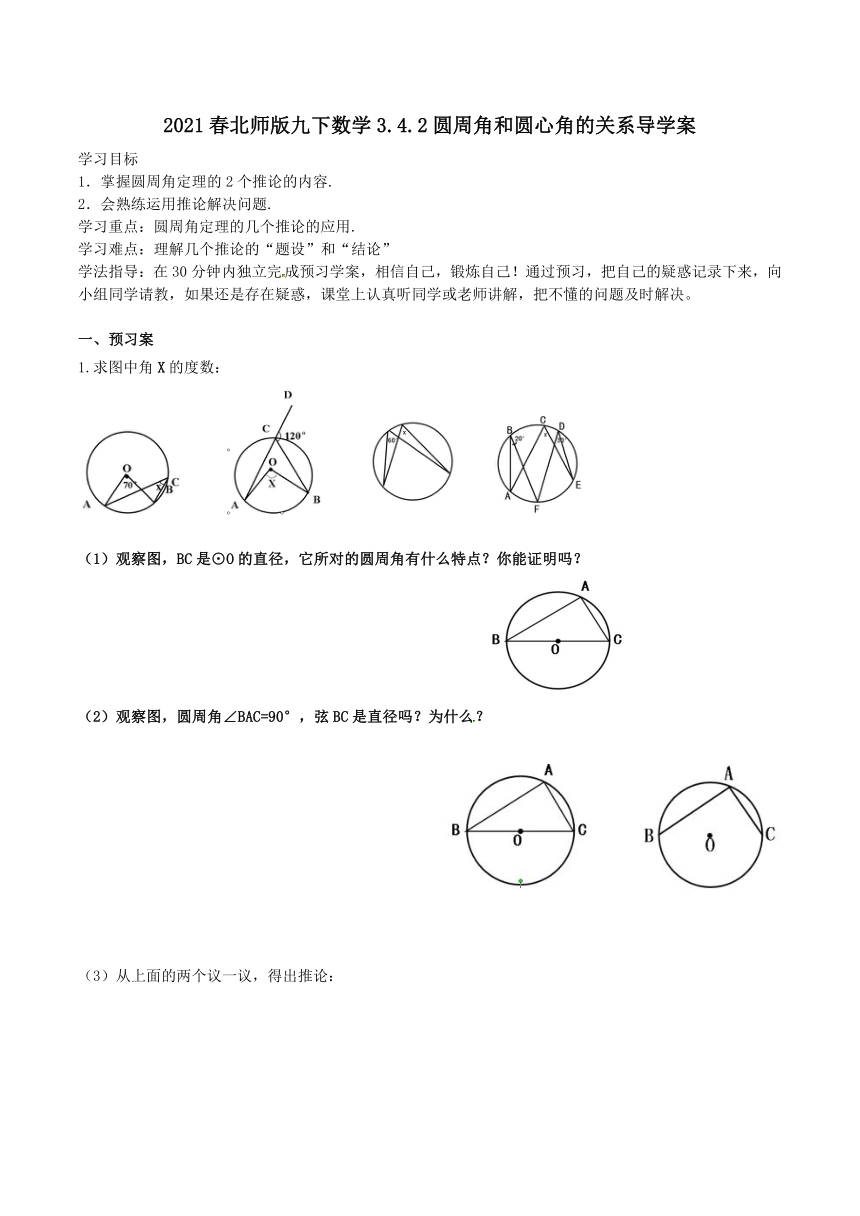
1.求图中角X的度数:
(1)观察图,BC是⊙O的直径,它所对的圆周角有什么特点?你能证明吗?
(2)观察图,圆周角∠BAC=90°,弦BC是直径吗?为什么?
(3)从上面的两个议一议,得出推论:
二、探究案
活动内容:
(1)小明想用直角尺检查某些工件是否恰好为半圆形.下面所示的四种圆弧形,你能判断哪个是半圆形?为什么?
(2)如图,⊙O的直径AB=10cm,C为⊙O上的一点,∠B=30°,求AC的长.
(一)如图,A,B,C,D是⊙O上的四点,AC为⊙O的直径,请问∠BAD与∠BCD之间有什么关系?为什么?
(二)如图,C点的位置发生了变化,∠BAD与∠BCD之间有的关系还成立吗?为什么?
(三)圆内接四边形概念与性质探索
如图,两个四边形ABCD有什么共同的特点?
得出定义:四边形ABCD的的四个顶点都在⊙O上,这样的四边形叫做圆内接四边形;
这个圆叫做四边形的外接圆.
推论:
三.达标测试
1.已知如图所示,是的直径,,,则___________.
2.如图,在中,的平分线交于,交的外接圆于.连接、.
(1)图中相等的圆周角有:_____________________;
(2)相等的线段有:__________________________.
3.如图,在足球比赛场上,甲、乙两名队员互相配合向对方球门进攻,当甲带球冲到点时,乙已跟随冲到点.从数学角度看,此时甲是自己射门好,还是将球传给乙,让乙射门好:__________,说明你的理由:_______________________.
4.如图,点、、在上,,则的度数是____________.
5.如图,每张方格纸上都画有一个圆,只用不带刻度的直尺就能确定圆心位置的是( ).
6.如图,已知中,为直径,,弦,的平分线交于,求、和的长.
7.如图,是的半径,以为直径的与的弦相交于点,则与有什么关系?为什么?
8.如图,点、、、在上,点在的内部,四边形为平行四边形,则与的和是多少?
达标测试答案
1.
2.(1),,.
(2).
3.乙射门好,乙射门的角度大.
4. 5.B
6.,.
观察与思考
7.解:.
理由:连接. 是的直径,,
,.
拓展与延伸
8.
学习目标
1.掌握圆周角定理的2个推论的内容.
2.会熟练运用推论解决问题.
学习重点:圆周角定理的几个推论的应用.
学习难点:理解几个推论的“题设”和“结论”
学法指导:在30分钟内独立完成预习学案,相信自己,锻炼自己!通过预习,把自己的疑惑记录下来,向小组同学请教,如果还是存在疑惑,课堂上认真听同学或老师讲解,把不懂的问题及时解决。
一、预习案
1.求图中角X的度数:
(1)观察图,BC是⊙O的直径,它所对的圆周角有什么特点?你能证明吗?
(2)观察图,圆周角∠BAC=90°,弦BC是直径吗?为什么?
(3)从上面的两个议一议,得出推论:
二、探究案
活动内容:
(1)小明想用直角尺检查某些工件是否恰好为半圆形.下面所示的四种圆弧形,你能判断哪个是半圆形?为什么?
(2)如图,⊙O的直径AB=10cm,C为⊙O上的一点,∠B=30°,求AC的长.
(一)如图,A,B,C,D是⊙O上的四点,AC为⊙O的直径,请问∠BAD与∠BCD之间有什么关系?为什么?
(二)如图,C点的位置发生了变化,∠BAD与∠BCD之间有的关系还成立吗?为什么?
(三)圆内接四边形概念与性质探索
如图,两个四边形ABCD有什么共同的特点?
得出定义:四边形ABCD的的四个顶点都在⊙O上,这样的四边形叫做圆内接四边形;
这个圆叫做四边形的外接圆.
推论:
三.达标测试
1.已知如图所示,是的直径,,,则___________.
2.如图,在中,的平分线交于,交的外接圆于.连接、.
(1)图中相等的圆周角有:_____________________;
(2)相等的线段有:__________________________.
3.如图,在足球比赛场上,甲、乙两名队员互相配合向对方球门进攻,当甲带球冲到点时,乙已跟随冲到点.从数学角度看,此时甲是自己射门好,还是将球传给乙,让乙射门好:__________,说明你的理由:_______________________.
4.如图,点、、在上,,则的度数是____________.
5.如图,每张方格纸上都画有一个圆,只用不带刻度的直尺就能确定圆心位置的是( ).
6.如图,已知中,为直径,,弦,的平分线交于,求、和的长.
7.如图,是的半径,以为直径的与的弦相交于点,则与有什么关系?为什么?
8.如图,点、、、在上,点在的内部,四边形为平行四边形,则与的和是多少?
达标测试答案
1.
2.(1),,.
(2).
3.乙射门好,乙射门的角度大.
4. 5.B
6.,.
观察与思考
7.解:.
理由:连接. 是的直径,,
,.
拓展与延伸
8.
