苏科版八年级数学上册 1.3 探索三角形全等的条件(共14张PPT)
文档属性
| 名称 | 苏科版八年级数学上册 1.3 探索三角形全等的条件(共14张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-15 09:05:56 | ||
图片预览





文档简介
(共14张PPT)
苏科版八年级(上册)
(一)创设情景,激发求知欲望
港下中学为了提高学校硬件环境,到力达公司定做了一批三角形架用于教室摆放电视机,要求是所有的三角形必须全等。后勤部门为了使产品顺利过关,提出了明确的要求:要逐一检查三角形的三条边、三个角是不是都相等。部门职员小李提出了质疑:分别检查三条边、三个角这6个数据固然可以,但为了提高效率,是不是可以找到一个更好的方法,只量一个数据可以吗?两个呢?……
(二)引导活动,揭示知识产生过程 (活动一)
问题2当两个三角形只有2组边或角相等时,它们
全等吗?
问题3当两个三角形有3组边或角相等时,它们全
等吗?
问题1当两个三角形只有一组边或角相等时,它们
全等吗?
(二)引导活动,揭示知识产生过程(活动二)
各小组每人用一张长方形纸剪一个直角三角形(只用直尺和剪刀),怎样才能使各小组内部剪下的直角三角形都全等呢?
(二)引导活动,揭示知识产生过程(活动三)
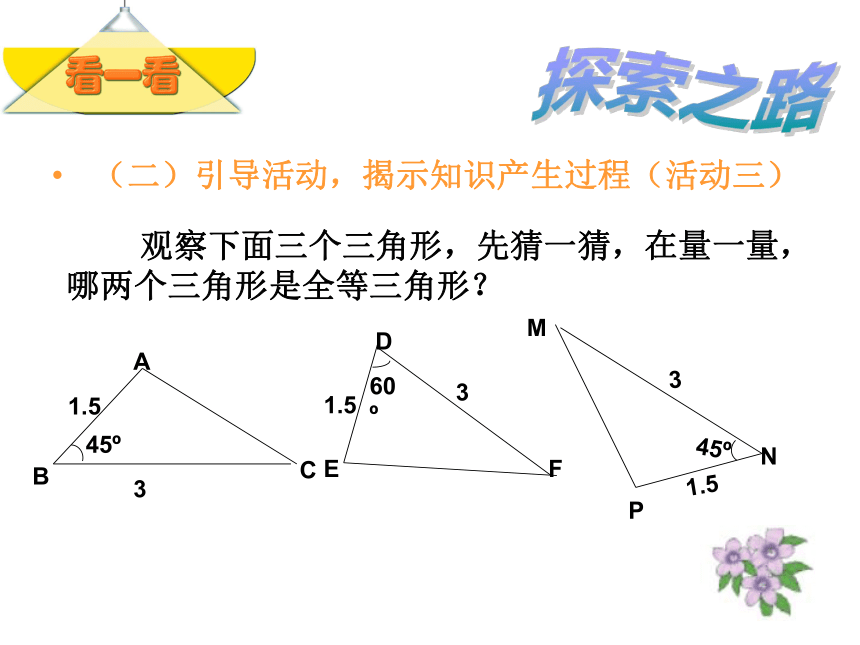
观察下面三个三角形,先猜一猜,在量一量,哪两个三角形是全等三角形?
A
B
C
1.5
3
45
D
E
F
1.5
3
60
1.5
3
45
M
N
P
(二)引导活动,揭示知识产生过程(活动四)
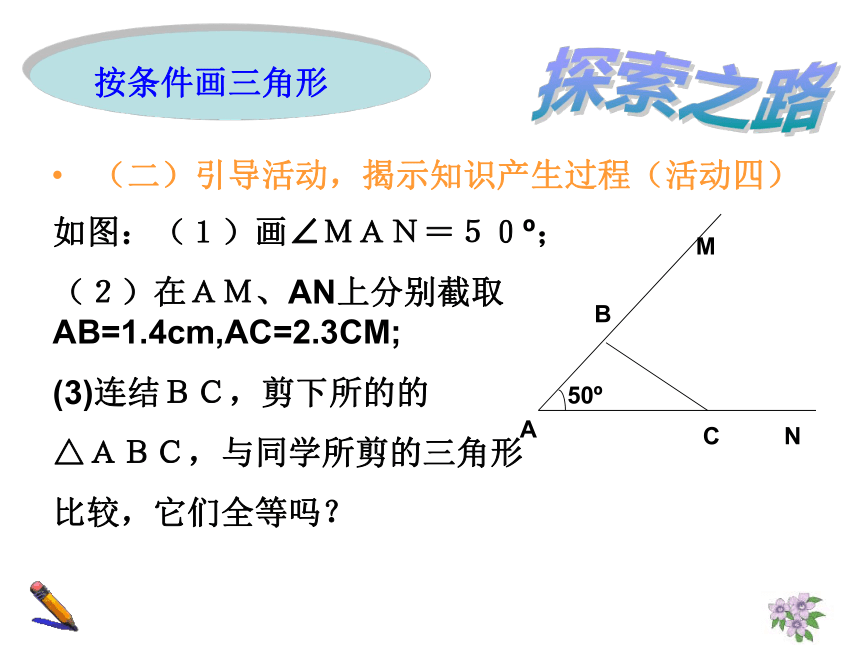
按条件画三角形
如图:(1)画∠MAN=50 ;
(2)在AM、AN上分别截取 AB=1.4cm,AC=2.3CM;
(3)连结BC,剪下所的的
△ABC,与同学所剪的三角形
比较,它们全等吗?
A
B
C
M
N
50
(二)引导活动,揭示揭示规律
两边和它们的夹角对应相等的两个三角形全等.简写成“边角边”或“SAS”
(三)例题教学,发挥示范功能
例题1:
如图,AB=AD,
∠BAC=∠DAC,请问:
△ABC和 △ADC是否
全等?为什么?
问题1: 请说说本例已知了哪些条件,还差一个什么条件,怎么办?
问题2: 你能用“因为……根据……所以……”的表达形式说说本题
的说理过程吗?
问题3: △ADC可以看成是由△ABC经过怎样的图形变换得到的?
变式与引伸
如图,AB=AD,∠BAC=∠DAC,请问:
△ABC和 △ADC是否全等?为什么?
问题1:△ABC与△ADC全等了,你又能得到哪些结论?
问题2:连接BD交AC于O,你能说明△BOC与△DOC
全等吗?若全等,你又能得到哪些结论?
O
练习巩固
AB DC
≌
练习巩固
讨论 :将“两边和它们的夹角对应相等”
改为“两边和其中一边的对角相等”这样的两个三角形还全等吗?
生活中的数学
春节期间,几名学生在钵池山公园,测量一池塘两端A,B的距离,设计了如下方案:如图,先在平地上取了一个可直接到达A,B的点C,再连接AC,BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测DE的长即为AB的距离,你认为这种方案可行吗 并加以说明.
A
E
B
C
D
练习巩固
(四)课堂小结,建立知识体系。
1、经历了剪纸、测量、画图等方法探索三角形
全等条件的活动过程、积累数学活动经验。
2、归纳得出了两个三角形全等的条件——SAS,
知到了有两边和其中一边的对角对应相等的两个
三角形不一定全等,初步发展了推理能力。
苏科版八年级(上册)
(一)创设情景,激发求知欲望
港下中学为了提高学校硬件环境,到力达公司定做了一批三角形架用于教室摆放电视机,要求是所有的三角形必须全等。后勤部门为了使产品顺利过关,提出了明确的要求:要逐一检查三角形的三条边、三个角是不是都相等。部门职员小李提出了质疑:分别检查三条边、三个角这6个数据固然可以,但为了提高效率,是不是可以找到一个更好的方法,只量一个数据可以吗?两个呢?……
(二)引导活动,揭示知识产生过程 (活动一)
问题2当两个三角形只有2组边或角相等时,它们
全等吗?
问题3当两个三角形有3组边或角相等时,它们全
等吗?
问题1当两个三角形只有一组边或角相等时,它们
全等吗?
(二)引导活动,揭示知识产生过程(活动二)
各小组每人用一张长方形纸剪一个直角三角形(只用直尺和剪刀),怎样才能使各小组内部剪下的直角三角形都全等呢?
(二)引导活动,揭示知识产生过程(活动三)
观察下面三个三角形,先猜一猜,在量一量,哪两个三角形是全等三角形?
A
B
C
1.5
3
45
D
E
F
1.5
3
60
1.5
3
45
M
N
P
(二)引导活动,揭示知识产生过程(活动四)
按条件画三角形
如图:(1)画∠MAN=50 ;
(2)在AM、AN上分别截取 AB=1.4cm,AC=2.3CM;
(3)连结BC,剪下所的的
△ABC,与同学所剪的三角形
比较,它们全等吗?
A
B
C
M
N
50
(二)引导活动,揭示揭示规律
两边和它们的夹角对应相等的两个三角形全等.简写成“边角边”或“SAS”
(三)例题教学,发挥示范功能
例题1:
如图,AB=AD,
∠BAC=∠DAC,请问:
△ABC和 △ADC是否
全等?为什么?
问题1: 请说说本例已知了哪些条件,还差一个什么条件,怎么办?
问题2: 你能用“因为……根据……所以……”的表达形式说说本题
的说理过程吗?
问题3: △ADC可以看成是由△ABC经过怎样的图形变换得到的?
变式与引伸
如图,AB=AD,∠BAC=∠DAC,请问:
△ABC和 △ADC是否全等?为什么?
问题1:△ABC与△ADC全等了,你又能得到哪些结论?
问题2:连接BD交AC于O,你能说明△BOC与△DOC
全等吗?若全等,你又能得到哪些结论?
O
练习巩固
AB DC
≌
练习巩固
讨论 :将“两边和它们的夹角对应相等”
改为“两边和其中一边的对角相等”这样的两个三角形还全等吗?
生活中的数学
春节期间,几名学生在钵池山公园,测量一池塘两端A,B的距离,设计了如下方案:如图,先在平地上取了一个可直接到达A,B的点C,再连接AC,BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测DE的长即为AB的距离,你认为这种方案可行吗 并加以说明.
A
E
B
C
D
练习巩固
(四)课堂小结,建立知识体系。
1、经历了剪纸、测量、画图等方法探索三角形
全等条件的活动过程、积累数学活动经验。
2、归纳得出了两个三角形全等的条件——SAS,
知到了有两边和其中一边的对角对应相等的两个
三角形不一定全等,初步发展了推理能力。
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
