苏科版八年级数学上册 4.3 实数(共17张PPT)
文档属性
| 名称 | 苏科版八年级数学上册 4.3 实数(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 755.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-15 00:00:00 | ||
图片预览



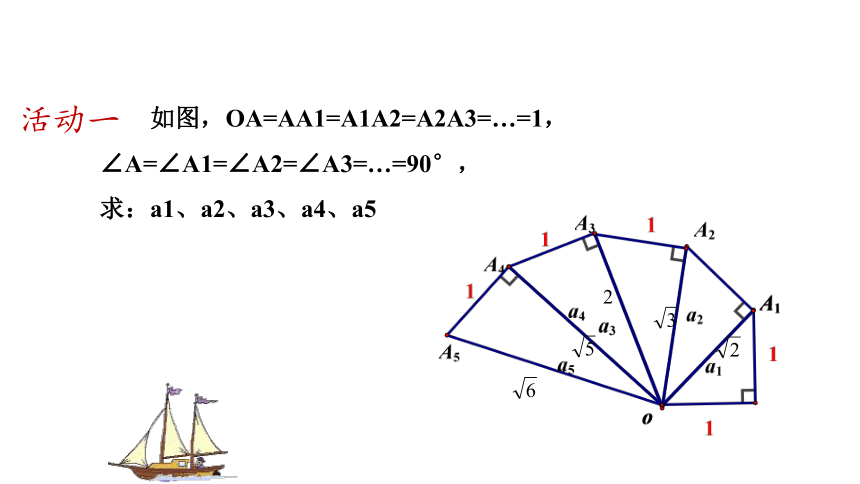

文档简介
(共17张PPT)
4.3 实 数 (1)
一、学习目标:
1、了解无理数和实数的概念,会判断一个数是有理数还是无理数;
2、知道实数和数轴上的点一一对应,并能在数轴上表示一个实数。
有效学习——知识的生成。
一、自学内容及时间:
内容:课本P101 时间:6min
二、自学任务:
1、完成课本尝试中第1题;
2、仿照课本,画出线段长为 的线段(铅笔、三角板和刻度尺作图),
说说你的方法;
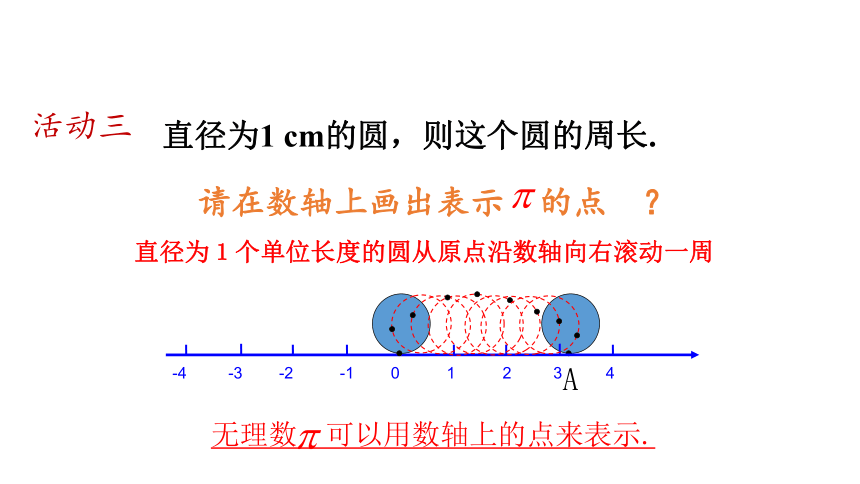
3、直径为1 cm的圆的周长__________、面积____________ .
4、请举出几个无理数的例子:_______________。
如图,OA=AA1=A1A2=A2A3=…=1,∠A=∠A1=∠A2=∠A3=…=90°,
求:a1、a2、a3、a4、a5
活动一
你能画出长度分是分别为 cm, cm,
cm,……的线段吗?
活动二
活动三
请在数轴上画出表示 的点 ?
直径为1个单位长度的圆从原点沿数轴向右滚动一周
-4
-2
0
1
2
3
4
-1
-3
无理数 可以用数轴上的点来表示.
A
直径为1 cm的圆,则这个圆的周长.
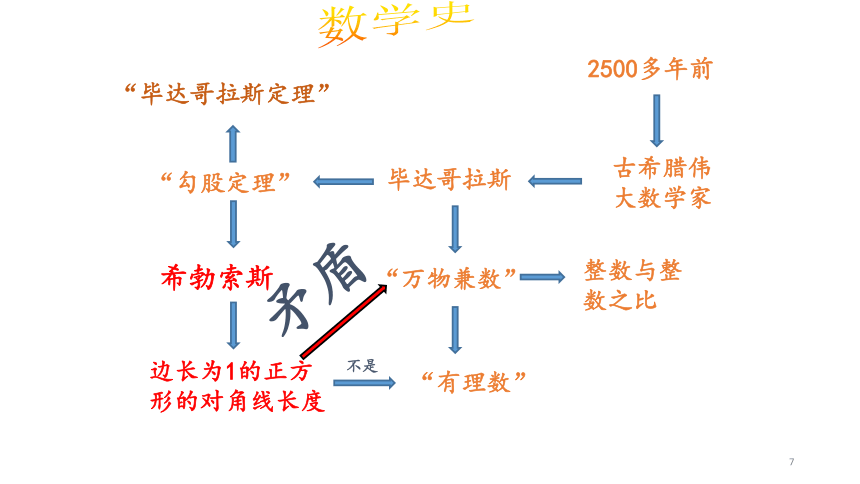
2500多年前
古希腊伟
大数学家
毕达哥拉斯
“勾股定理”
“毕达哥拉斯定理”
“万物兼数”
整数与整数之比
“有理数”
希勃索斯
边长为1的正方形的对角线长度
不是
矛盾
7
有效学习——知识的生成。
1、下列数中,无理数有哪些?
2、判断正误,若不对,请说明理由,并加以改正.
(1)无理数都是无限小数. (2)带根号的数不一定是无理数.
(3)无限小数都是无理数. (4)不带根号的数一定是有理数.
√
√
√
√
√
√
×
×
思考:无理数有哪些常见的形式?
①带根号且开方开不尽的结果
0.1010010 001…
②π;以及一些含有π 的数
③构造的有规律且无限不循环小数(注意加省略号)
2π
一、自学内容及时间:
内容:课本P102 时间:5min
二、自学任务
1、 统称为实数。
2、请将实数进行分类,完成在学案上。
3、在数轴上画出表示 的点,尝试一下!
4、_______与数轴上的点一一对应
有效学习——知识的生成。
有理数和无理数
实数
10
正有理数
负有理数
零
负无理数
正无理数
实 数
无限不循环小数
有限小数或
无限循环小数
1.实数的分类:
有理数
无理数
按定义分类:
正有理数
负有理数
零
负无理数
正无理数
正实数
负实数
实 数
2.实数还有别的分类方式吗?
按正负性分类:
12
把下列各数填入相应的集合内:
(1)有理数集合:
(2)无理数集合:
(3)整数集合:
(4)负数集合:
(5)分数集合:
(6)实数集合:
13
有效学习——知识的生成。
1、在数轴上画出表示的 点.
2 3
<
>
>
1、
拓展:
2、
当堂检测
1、把下列各数填入相应的括号内:
(1)有理数:{ … }
(2)无理数:{ … }
(3)正实数:{ …}
(4)负实数:{ … }
0.121121112…
0.121121112…
0.121121112…
0
2
3
1
-1
2、在数轴上画出表示 的点
4
归纳小结
(1)实数
___________
_______________________________________
1、有理数和无理数统称为
2、实数的分类
______数
________数
________数
0
______数 _________数
________数
(2)实数
_____实数
_____
_____实数
有理
无理
正有理
负有理
有限小数或无限循环小数
___________________________________________
正无理
负无理
无限不循环小数
正
0
负
实数
3、实数与数轴上的点是 ___ 的.
一一对应
4.3 实 数 (1)
一、学习目标:
1、了解无理数和实数的概念,会判断一个数是有理数还是无理数;
2、知道实数和数轴上的点一一对应,并能在数轴上表示一个实数。
有效学习——知识的生成。
一、自学内容及时间:
内容:课本P101 时间:6min
二、自学任务:
1、完成课本尝试中第1题;
2、仿照课本,画出线段长为 的线段(铅笔、三角板和刻度尺作图),
说说你的方法;
3、直径为1 cm的圆的周长__________、面积____________ .
4、请举出几个无理数的例子:_______________。
如图,OA=AA1=A1A2=A2A3=…=1,∠A=∠A1=∠A2=∠A3=…=90°,
求:a1、a2、a3、a4、a5
活动一
你能画出长度分是分别为 cm, cm,
cm,……的线段吗?
活动二
活动三
请在数轴上画出表示 的点 ?
直径为1个单位长度的圆从原点沿数轴向右滚动一周
-4
-2
0
1
2
3
4
-1
-3
无理数 可以用数轴上的点来表示.
A
直径为1 cm的圆,则这个圆的周长.
2500多年前
古希腊伟
大数学家
毕达哥拉斯
“勾股定理”
“毕达哥拉斯定理”
“万物兼数”
整数与整数之比
“有理数”
希勃索斯
边长为1的正方形的对角线长度
不是
矛盾
7
有效学习——知识的生成。
1、下列数中,无理数有哪些?
2、判断正误,若不对,请说明理由,并加以改正.
(1)无理数都是无限小数. (2)带根号的数不一定是无理数.
(3)无限小数都是无理数. (4)不带根号的数一定是有理数.
√
√
√
√
√
√
×
×
思考:无理数有哪些常见的形式?
①带根号且开方开不尽的结果
0.1010010 001…
②π;以及一些含有π 的数
③构造的有规律且无限不循环小数(注意加省略号)
2π
一、自学内容及时间:
内容:课本P102 时间:5min
二、自学任务
1、 统称为实数。
2、请将实数进行分类,完成在学案上。
3、在数轴上画出表示 的点,尝试一下!
4、_______与数轴上的点一一对应
有效学习——知识的生成。
有理数和无理数
实数
10
正有理数
负有理数
零
负无理数
正无理数
实 数
无限不循环小数
有限小数或
无限循环小数
1.实数的分类:
有理数
无理数
按定义分类:
正有理数
负有理数
零
负无理数
正无理数
正实数
负实数
实 数
2.实数还有别的分类方式吗?
按正负性分类:
12
把下列各数填入相应的集合内:
(1)有理数集合:
(2)无理数集合:
(3)整数集合:
(4)负数集合:
(5)分数集合:
(6)实数集合:
13
有效学习——知识的生成。
1、在数轴上画出表示的 点.
2 3
<
>
>
1、
拓展:
2、
当堂检测
1、把下列各数填入相应的括号内:
(1)有理数:{ … }
(2)无理数:{ … }
(3)正实数:{ …}
(4)负实数:{ … }
0.121121112…
0.121121112…
0.121121112…
0
2
3
1
-1
2、在数轴上画出表示 的点
4
归纳小结
(1)实数
___________
_______________________________________
1、有理数和无理数统称为
2、实数的分类
______数
________数
________数
0
______数 _________数
________数
(2)实数
_____实数
_____
_____实数
有理
无理
正有理
负有理
有限小数或无限循环小数
___________________________________________
正无理
负无理
无限不循环小数
正
0
负
实数
3、实数与数轴上的点是 ___ 的.
一一对应
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
