苏科版八年级数学上册 3.1 勾股定理(共20张PPT)
文档属性
| 名称 | 苏科版八年级数学上册 3.1 勾股定理(共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-15 09:25:36 | ||
图片预览







文档简介
(共20张PPT)
勾股定理
南京玄武湖东西隧道与中央路北段及龙蟠路大致成直角三角形,从A处到C处,如果直接走湖底隧道AC,比绕道AB(5km)和BC (3km)减少多少行程
A
B
C
A
B
C
毕达哥拉斯
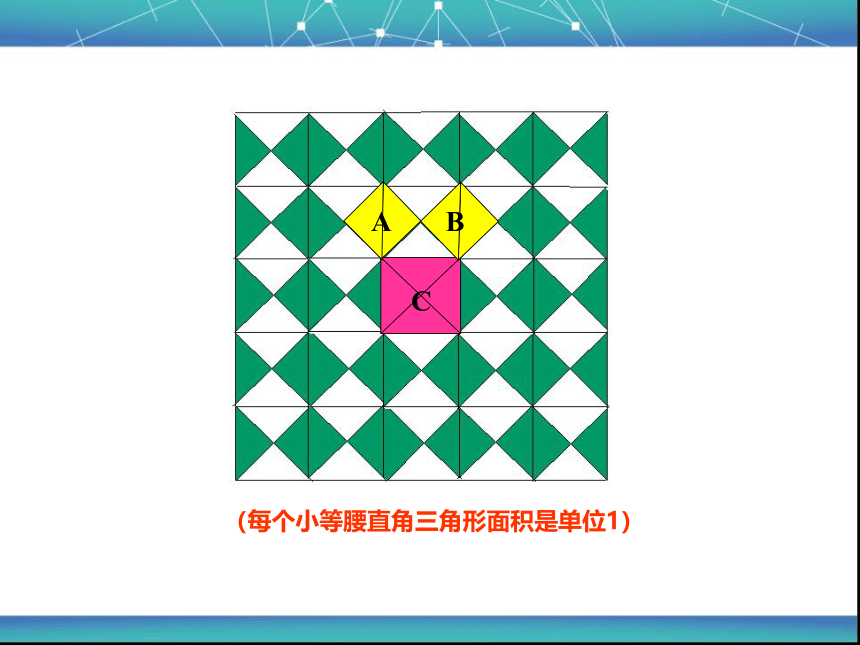
相传2500年前,毕达哥拉斯有一次在朋友家里做客时,偶然发现朋友家用砖铺成的地面有一些特殊的基本图形,继而研究发现了直角三角形三边的某种数量关系。
A
B
C
(每个小等腰直角三角形面积是单位1)
A
B
C
正方形A,B,C的面积有什么关系?
以a,b为直角边,c为斜边的直角三角形的三边关系是?
B
A
C
结论:
A的面积是 个单位面积.
B的面积是 个单位面积.
C的面积是 个单位面积.
25
9
16
(图中每个小方格是1个单位面积)
其它网格直角三角形是否也存在这种关系?
即:
a
c
b
在学习单网格中任意画一个格点直角三角形,以三角形三边a,b,c(a结论:
即:
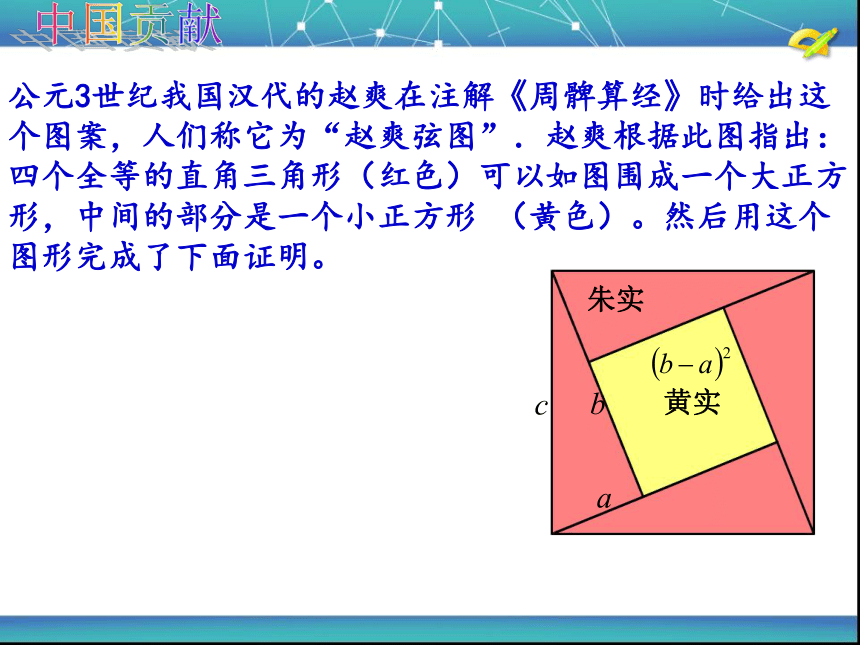
公元3世纪我国汉代的赵爽在注解《周髀算经》时给出这个图案,人们称它为“赵爽弦图”.赵爽根据此图指出:四个全等的直角三角形(红色)可以如图围成一个大正方形,中间的部分是一个小正方形 (黄色)。然后用这个图形完成了下面证明。
c
b
a
黄实
朱实
观察最大的正方形?你有几种方法表示它的面积?
∵
2002年在北京召开的国际数学家大会(ICM2002)就利用了赵爽弦图作为大会会标,远看像旋转的纸风车,非常简洁优美。
勾股定理
直角三角形两条直角边a、b的平方和等于斜边c的平方.
勾
股
弦
勾股史话
我国是最早了解勾股定理的国家之一.
早在三千多年前,周朝的数学家商高就提出,
将一根直尺折成一个直角,如果勾等于三,
股等于四,那么弦就等于五,即“勾三、股四、
弦五”.它被记载于我国古代著名的数学著作
《周髀算经》中.在这本书中的另一处,还记载了勾股定理的一般形式.这一发现,至少早于古希腊人500多年.作为一名中国人,我们应为我国古人的博学和多思而感到自豪!
勾股定理是人类文明的成果,几乎所有拥有古代文化的民族和国家都对勾股定理有所研究.在地球以外是否存在生命这个问题上,我国数学家华罗庚曾认为,如果外星人也拥有文明的话,我们可以用“勾股定理”的图形,作为人类探寻“外星人”并与“外星人”联系的“语言”.
例1:如图,在Rt△ABC和Rt△ABD中,∠C=∠ABD=90°,AC=4,BC=3,AD=13, 求BD
1.直接说出直角三角形未知边的长:
5
12
x
17
8
X=13
①
②
x
X=15
2、下图中的三角形是直角三角形,其余是正方形,说出下列图中字母所表示的正方形面积.
=625
225
400
A
225
81
B
=144
如图,所有的三角形都是直角三角形,四边形都是正方形,已知正方形A,B,C,D 的边长分别是12,16,9,12.最大正方形E 的面积是 。
A
B
C
D
E
625
南京玄武湖东西隧道与中央路北段及龙蟠路大致成直角三角形,从A处到C处,如果直接走湖底隧道AC,比绕道AB(5km)和BC (3km)减少多少行程
A
B
C
如图, 和 都不是直角三角形,分别以
和 的各边为一边向三角形外部作正方形,其中两个小正方形的面积和等于大正方形的面积么?
想一想
01
勾股定理有关知识
03
从特殊到一般,割补法
02
数形结合
思想
谢谢大家光临指导
谢谢大家光临指导!
勾股定理
南京玄武湖东西隧道与中央路北段及龙蟠路大致成直角三角形,从A处到C处,如果直接走湖底隧道AC,比绕道AB(5km)和BC (3km)减少多少行程
A
B
C
A
B
C
毕达哥拉斯
相传2500年前,毕达哥拉斯有一次在朋友家里做客时,偶然发现朋友家用砖铺成的地面有一些特殊的基本图形,继而研究发现了直角三角形三边的某种数量关系。
A
B
C
(每个小等腰直角三角形面积是单位1)
A
B
C
正方形A,B,C的面积有什么关系?
以a,b为直角边,c为斜边的直角三角形的三边关系是?
B
A
C
结论:
A的面积是 个单位面积.
B的面积是 个单位面积.
C的面积是 个单位面积.
25
9
16
(图中每个小方格是1个单位面积)
其它网格直角三角形是否也存在这种关系?
即:
a
c
b
在学习单网格中任意画一个格点直角三角形,以三角形三边a,b,c(a
即:
公元3世纪我国汉代的赵爽在注解《周髀算经》时给出这个图案,人们称它为“赵爽弦图”.赵爽根据此图指出:四个全等的直角三角形(红色)可以如图围成一个大正方形,中间的部分是一个小正方形 (黄色)。然后用这个图形完成了下面证明。
c
b
a
黄实
朱实
观察最大的正方形?你有几种方法表示它的面积?
∵
2002年在北京召开的国际数学家大会(ICM2002)就利用了赵爽弦图作为大会会标,远看像旋转的纸风车,非常简洁优美。
勾股定理
直角三角形两条直角边a、b的平方和等于斜边c的平方.
勾
股
弦
勾股史话
我国是最早了解勾股定理的国家之一.
早在三千多年前,周朝的数学家商高就提出,
将一根直尺折成一个直角,如果勾等于三,
股等于四,那么弦就等于五,即“勾三、股四、
弦五”.它被记载于我国古代著名的数学著作
《周髀算经》中.在这本书中的另一处,还记载了勾股定理的一般形式.这一发现,至少早于古希腊人500多年.作为一名中国人,我们应为我国古人的博学和多思而感到自豪!
勾股定理是人类文明的成果,几乎所有拥有古代文化的民族和国家都对勾股定理有所研究.在地球以外是否存在生命这个问题上,我国数学家华罗庚曾认为,如果外星人也拥有文明的话,我们可以用“勾股定理”的图形,作为人类探寻“外星人”并与“外星人”联系的“语言”.
例1:如图,在Rt△ABC和Rt△ABD中,∠C=∠ABD=90°,AC=4,BC=3,AD=13, 求BD
1.直接说出直角三角形未知边的长:
5
12
x
17
8
X=13
①
②
x
X=15
2、下图中的三角形是直角三角形,其余是正方形,说出下列图中字母所表示的正方形面积.
=625
225
400
A
225
81
B
=144
如图,所有的三角形都是直角三角形,四边形都是正方形,已知正方形A,B,C,D 的边长分别是12,16,9,12.最大正方形E 的面积是 。
A
B
C
D
E
625
南京玄武湖东西隧道与中央路北段及龙蟠路大致成直角三角形,从A处到C处,如果直接走湖底隧道AC,比绕道AB(5km)和BC (3km)减少多少行程
A
B
C
如图, 和 都不是直角三角形,分别以
和 的各边为一边向三角形外部作正方形,其中两个小正方形的面积和等于大正方形的面积么?
想一想
01
勾股定理有关知识
03
从特殊到一般,割补法
02
数形结合
思想
谢谢大家光临指导
谢谢大家光临指导!
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
