苏科版九年级数学上册 1.1 一元二次方程(共16张PPT)
文档属性
| 名称 | 苏科版九年级数学上册 1.1 一元二次方程(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-15 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
1.1一元二次方程
问题情境
问题1.小陈老师坐车从靖江到无锡去参加优课比赛,经测量两地相距70km,全程平均车速为60km/h,设驾车时间为t h,可得方程____________。
速度×时间=路程
→
→
问题情境
问题2.到达比赛地点学校后,老师了解到,校园
布局可近似看做长方形,经测量,其长比宽多100米。
(1)设学校长为a米,宽为b米,可得方程_________;
(2)学校占地约120000平方米,设学校的宽为x米,长为(x+100)米,可得方程 ___________________。
(2)学校计划明年将绿化面积从去年的2万平方米增加到2.88万平方米,设绿化面积平均每年增长的百分率是x,可得方程______________ 。
问题情境
问题3.进入校园后,老师发现校园绿化非常好,一打听,本校老师介绍:
(1)去年时校园绿化面积约2万平方米,今年增加到
2.4万平方米,设绿化面积平均每年增长的百分率是x,
可得方程_______________;
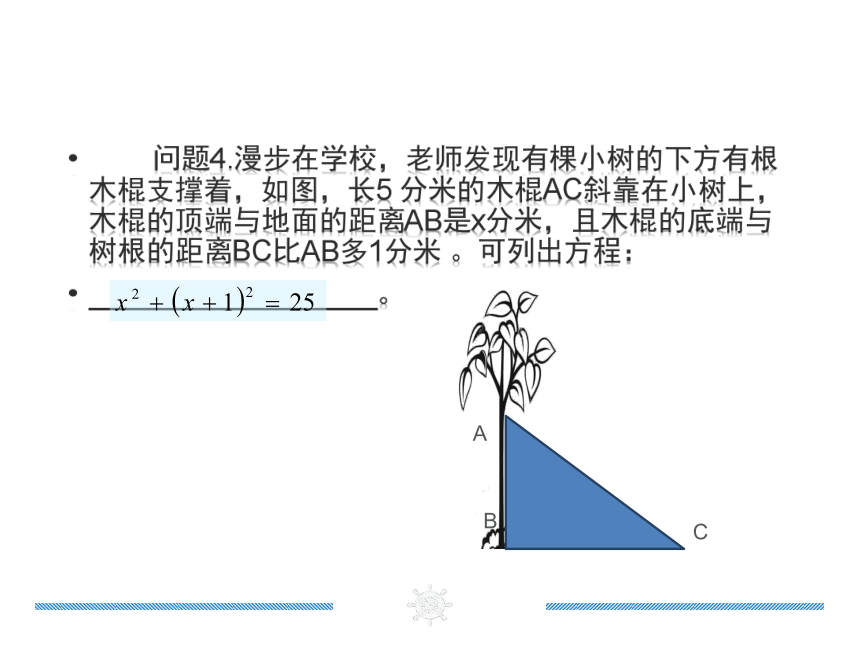
问题4.漫步在学校,老师发现有棵小树的下方有根木棍支撑着,如图,长5 分米的木棍AC斜靠在小树上,木棍的顶端与地面的距离AB是x分米,且木棍的底端与树根的距离BC比AB多1分米 。可列出方程:
__________________。
问题情境
A
B
C
探究新知
分式方程
二元一次方程
一元一次方程
①
②
③
④
⑦
⑤
⑥
1.只含有一个未知数
2.未知数的最高次数是2
3.整式方程
特点:
这样的方程叫
一元二次方程
探索新知
类比
明辨是非
例1.下列方程中是一元二次方程的有______(填序号),是一元二次方程的请说明判断依据,不是一元二次方程的请说明理由。
×
√
√
×
×
1.先判定是否为整式方程
2.化简
3.是否只含有一个未知数
4.未知数的最高次数是否为2
探索
一元二次方程都可以化简为右边为0的形式。
注:方程左边按未知数次数递减的顺序排列。
一元二次方程的一般形式
b x 叫一次项
a x 2 叫二次项
c 叫常数项
一次项系数
二次项系数
a x2 + b x + c = 0
(a、b、c为常数 )
且a ≠ 0
学以致用
例2.将下列方程化成一元二次方程的一般形式,并写出它的二次项系数a、一次项系数b和常数项c。
(1)
(2)
(3)
(m,n为常数,且m≠0).
方法总结:先化简,再整理成一元二次方程的一般形式,注意项的系数要连同前面的符号。
挑战自我
1.某校图书馆的藏书在两年内从5万册增加到9.8万册,求该图书馆藏书平均每年增长的百分率.
解:设这两年的年平均增长率为x。
根据题意,可得方程:_____________________;
一般式:_____________________;
a=____;b=____;c=____。
用方程描述下列问题中数量之间的相等关系
挑战自我
2.如图,矩形花圃一面靠墙(墙足够长),另外三面所围的栅栏的总长度是19m,花圃的面积为24m2,试求花圃的长和宽。
解:设_____________________;
根据题意,得方程_____________________;
一般式:_____________________;
a=____;b=____;c=____。
挑战自我
3.正方形桌面的面积是2平方米,你能求出它的边长吗?
设正方形桌面边长是 x 米;
根据题意,可得方程:_________。
2
x
你知道这个方程的解吗?
解:设正方形桌面边长是 x米。
根据题意,可得方程:
解方程得:
因为正方形的边长为正数;
所以
答:正方形的边长为 米。
长方形面积问题:
增长率问题:
直角三角形三边关系问题:
互作评价问题:
欲知后事如何,且听下回分解。
课堂小结:
这节课你有哪些收获?
1.从具体问题抽象出一元二次方程;
3.一元二次方程的一般形式,会将方程化为一般式,并指出各项系数。
2.一元二次方程的概念,会判断一元二次方程;
1.1一元二次方程
问题情境
问题1.小陈老师坐车从靖江到无锡去参加优课比赛,经测量两地相距70km,全程平均车速为60km/h,设驾车时间为t h,可得方程____________。
速度×时间=路程
→
→
问题情境
问题2.到达比赛地点学校后,老师了解到,校园
布局可近似看做长方形,经测量,其长比宽多100米。
(1)设学校长为a米,宽为b米,可得方程_________;
(2)学校占地约120000平方米,设学校的宽为x米,长为(x+100)米,可得方程 ___________________。
(2)学校计划明年将绿化面积从去年的2万平方米增加到2.88万平方米,设绿化面积平均每年增长的百分率是x,可得方程______________ 。
问题情境
问题3.进入校园后,老师发现校园绿化非常好,一打听,本校老师介绍:
(1)去年时校园绿化面积约2万平方米,今年增加到
2.4万平方米,设绿化面积平均每年增长的百分率是x,
可得方程_______________;
问题4.漫步在学校,老师发现有棵小树的下方有根木棍支撑着,如图,长5 分米的木棍AC斜靠在小树上,木棍的顶端与地面的距离AB是x分米,且木棍的底端与树根的距离BC比AB多1分米 。可列出方程:
__________________。
问题情境
A
B
C
探究新知
分式方程
二元一次方程
一元一次方程
①
②
③
④
⑦
⑤
⑥
1.只含有一个未知数
2.未知数的最高次数是2
3.整式方程
特点:
这样的方程叫
一元二次方程
探索新知
类比
明辨是非
例1.下列方程中是一元二次方程的有______(填序号),是一元二次方程的请说明判断依据,不是一元二次方程的请说明理由。
×
√
√
×
×
1.先判定是否为整式方程
2.化简
3.是否只含有一个未知数
4.未知数的最高次数是否为2
探索
一元二次方程都可以化简为右边为0的形式。
注:方程左边按未知数次数递减的顺序排列。
一元二次方程的一般形式
b x 叫一次项
a x 2 叫二次项
c 叫常数项
一次项系数
二次项系数
a x2 + b x + c = 0
(a、b、c为常数 )
且a ≠ 0
学以致用
例2.将下列方程化成一元二次方程的一般形式,并写出它的二次项系数a、一次项系数b和常数项c。
(1)
(2)
(3)
(m,n为常数,且m≠0).
方法总结:先化简,再整理成一元二次方程的一般形式,注意项的系数要连同前面的符号。
挑战自我
1.某校图书馆的藏书在两年内从5万册增加到9.8万册,求该图书馆藏书平均每年增长的百分率.
解:设这两年的年平均增长率为x。
根据题意,可得方程:_____________________;
一般式:_____________________;
a=____;b=____;c=____。
用方程描述下列问题中数量之间的相等关系
挑战自我
2.如图,矩形花圃一面靠墙(墙足够长),另外三面所围的栅栏的总长度是19m,花圃的面积为24m2,试求花圃的长和宽。
解:设_____________________;
根据题意,得方程_____________________;
一般式:_____________________;
a=____;b=____;c=____。
挑战自我
3.正方形桌面的面积是2平方米,你能求出它的边长吗?
设正方形桌面边长是 x 米;
根据题意,可得方程:_________。
2
x
你知道这个方程的解吗?
解:设正方形桌面边长是 x米。
根据题意,可得方程:
解方程得:
因为正方形的边长为正数;
所以
答:正方形的边长为 米。
长方形面积问题:
增长率问题:
直角三角形三边关系问题:
互作评价问题:
欲知后事如何,且听下回分解。
课堂小结:
这节课你有哪些收获?
1.从具体问题抽象出一元二次方程;
3.一元二次方程的一般形式,会将方程化为一般式,并指出各项系数。
2.一元二次方程的概念,会判断一元二次方程;
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
