苏科版九年级数学上册 2.7 弧长及扇形的面积课件(22张)
文档属性
| 名称 | 苏科版九年级数学上册 2.7 弧长及扇形的面积课件(22张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 7.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-15 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
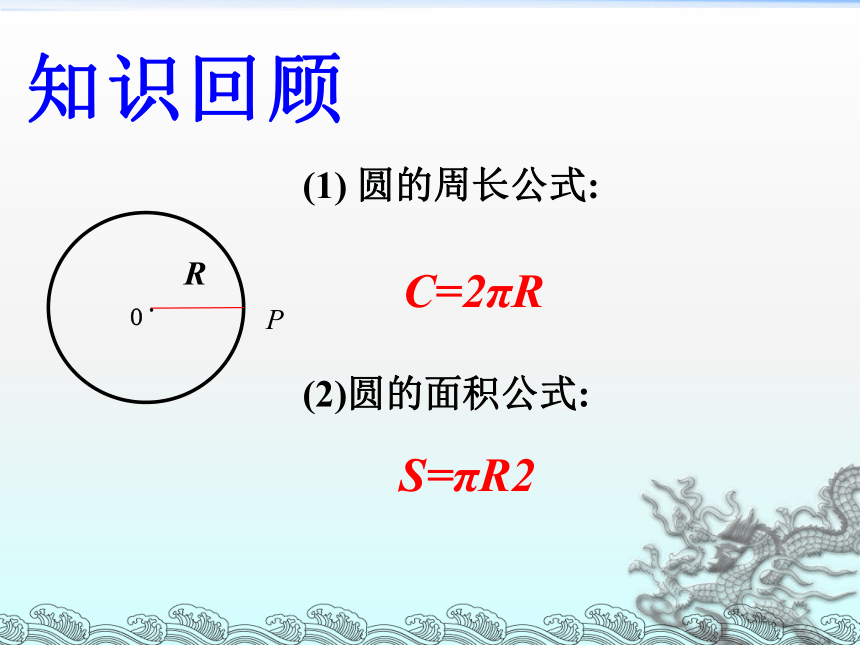
P
(1) 圆的周长公式:
(2)圆的面积公式:
C=2πR
S=πR2
R
.O
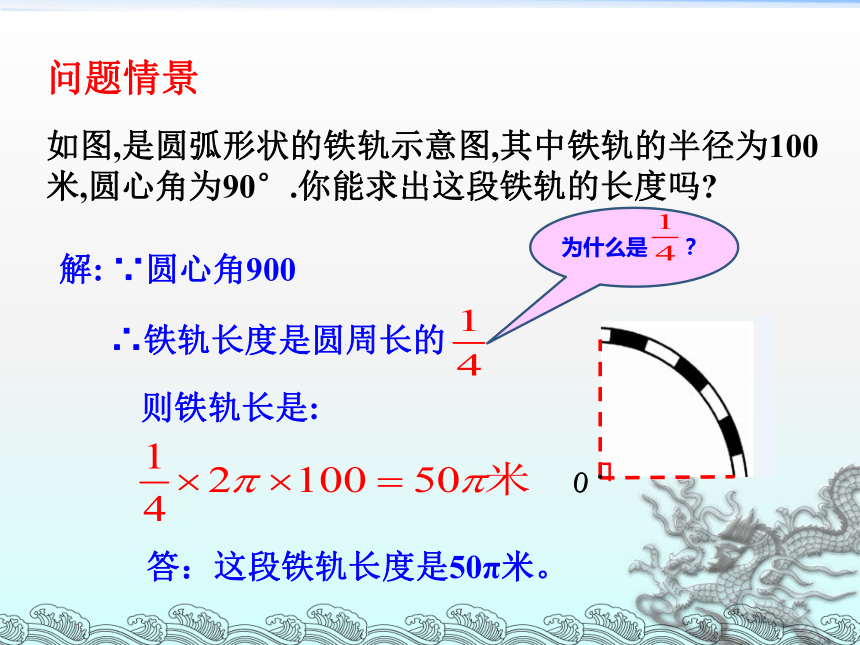
解: ∵圆心角900
∴铁轨长度是圆周长的
则铁轨长是:
如图,是圆弧形状的铁轨示意图,其中铁轨的半径为100米,圆心角为90°.你能求出这段铁轨的长度吗
问题情景
为什么是 ?
┐
.O
答:这段铁轨长度是50π米。
圆心角占整个周角的
所对弧长
思考1:请同学们计算半径为 R,圆心角分别为1800、 900、 10、n0 所对的弧长.
圆心角
1800
900
n0
圆的周长: C=2πR ; 圆心角 3600
R
·
1°
O
10
R
·
n°
O
R
·
180°
O
R
·
90°
O
┐
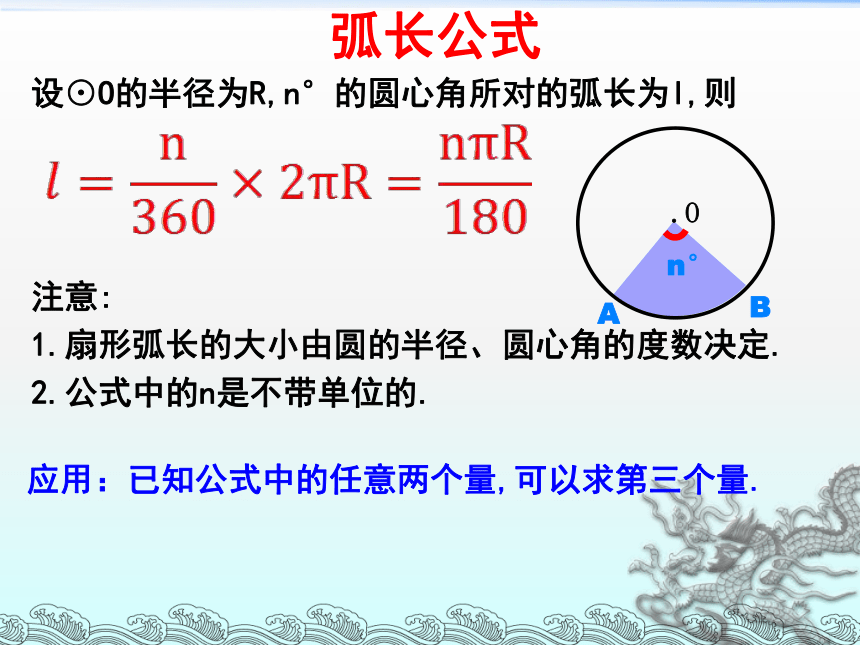
弧长公式
设⊙O的半径为R,n°的圆心角所对的弧长为l,则
A
B
n°
注意:
1.扇形弧长的大小由圆的半径、圆心角的度数决定.
2.公式中的n是不带单位的.
应用:已知公式中的任意两个量,可以求第三个量.
.O
1.已知扇形的圆心角为120°,半径为6,则扇形的弧长是( )
A. B. C. D.
解析:根据弧长公式 ,
可得扇形的弧长为 ,故选B
B
练一练
2.已知一条弧的半径为9,弧长为8π,那么这条弧所对的圆心角是为( )
A.200° B.160° C.120° D.80°
B
解析:∵弧长的公式 ,
∴弧长的公式 ,
解得 n=160 ,故选B.
3.已知扇形的圆心角为30°,弧长长为 ,则扇形的半径是( )
A.3cm B.4cm C.5cm D.6cm
D
解析:∵弧长的公式 ,
∴弧长的公式 ,
解得 R=6 ,故选D.
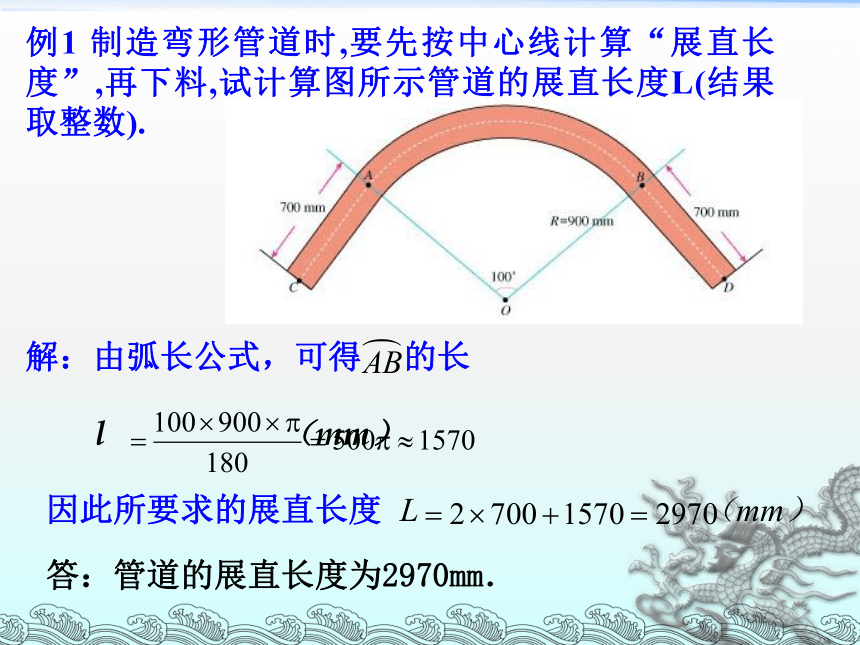
例1 制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(结果取整数).
解:由弧长公式,可得 的长
l (mm)
因此所要求的展直长度
L (mm)
答:管道的展直长度为2970mm.
由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形.
A
B
扇形
A
B
圆心角
半径
半径
弧
扇形的周长:两条半径和弧长.
.O
.O
小试牛刀
下列图形是扇形吗?
.O
.O
.O
.O
.O
.O
弓形
弓形
圆心角占整个周角的
所对扇形面积
思考2:请同学们计算半径为 R,圆心角分别为1800、 900、 10、n0 所对的扇形面积.
圆心角
1800
900
n0
R
·
1°
O
10
R
·
n°
O
R
·
180°
O
R
·
90°
O
圆的面积: S=πR2;圆心角 3600
┐
扇形面积公式
设⊙O半径为R,圆心角为n°的扇形的面积S扇形,则
A
B
n°
注意:
1.扇形面积的大小由圆的半径、圆心角的度数决定.
2.公式中的n是不带单位的.
应用:已知公式中的任意两个量,可以求第三个量.
.O
思考3:扇形的面积公式与弧长公式有联系吗?
如果扇形的半径为R的圆中,圆心角为no ,那么扇形面积的计算公式为:
扇形的弧长与扇形面积的关系为:
应用:已知公式中的任意两个量,可以求第三个量.
1、已知扇形的圆心角为120°,半径为2,则这个
扇形的面积S扇形=____.
2、已知扇形面积为 ,圆心角为60°,则这个
扇形的半径R=____.
3、已知半径为2cm的扇形,其弧长为 cm ,则这
个扇形的面积是_________.
做一做
例2 如图,水平放置的圆柱形排水管道的截面半径是0.6m,其中水面高0.3m,求截面上有水部分的面积S(结果保留小数点后两位).
0
B
A
C
D
S弓形= S扇形OAB-S△OAB
解:连接OA、OB,过圆心O作弦AB的垂直平分线,垂足为D,交 于点C.
∵OC=0.6,DC=0.3
∴OD=OC-DC=0.3
在Rt△OAD中,OA=0.6,OD=0.3
∴∠ OAD=30°, , AB=2AD=0.6
∴∠A OD=60°, ∠ AOB=120°
0
B
A
C
D
有水部分的面积:
答:截面上有水部分的面积为
如图,水平放置的圆柱形排水管道的截面半径是2,其中水面高3,求截面上有水部分的面积.
0
A
B
D
C
E
变式
S弓形= S扇形+S△
注意:
①当弓形面积小于半圆时
S弓形= S扇形-S△
②当弓形面积大于半圆时
S弓形= S扇形+S△
(07年山东)如图,⊙A、⊙B、⊙C、⊙D两两不相交,且半径都是2,求图中阴影部分的面积.
练习
答:图中阴影部分的面积为12π
拓展:如图,在△AOC中,∠AOC=900,∠C=150,以O为圆心,AO为半径的圆交AC与B点,若OA=6,求 的长.
A
C
B
O
解:连接OB
在Rt△AOC中,∠C=150,
∴∠OAB=900-∠C=750
由弧长公式,可得 的长
A
C
B
A′
C′
拓展:如图,把Rt△ABC的斜边放在直线 上,按顺时针方向转动一次,使它转到 的位置.若BC=1,∠A=300.求点A运动到A′位置时,求:(1)点A经过的路线长; (2)边AB扫过的面积;(3)Rt△ABC扫过的面积.
1.弧长和扇形面积公式:
2.扇形定义:由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.
3.弧长和扇形面积的应用:已知公式中的任意两个量,可以求第三个量.
课堂小结
P
(1) 圆的周长公式:
(2)圆的面积公式:
C=2πR
S=πR2
R
.O
解: ∵圆心角900
∴铁轨长度是圆周长的
则铁轨长是:
如图,是圆弧形状的铁轨示意图,其中铁轨的半径为100米,圆心角为90°.你能求出这段铁轨的长度吗
问题情景
为什么是 ?
┐
.O
答:这段铁轨长度是50π米。
圆心角占整个周角的
所对弧长
思考1:请同学们计算半径为 R,圆心角分别为1800、 900、 10、n0 所对的弧长.
圆心角
1800
900
n0
圆的周长: C=2πR ; 圆心角 3600
R
·
1°
O
10
R
·
n°
O
R
·
180°
O
R
·
90°
O
┐
弧长公式
设⊙O的半径为R,n°的圆心角所对的弧长为l,则
A
B
n°
注意:
1.扇形弧长的大小由圆的半径、圆心角的度数决定.
2.公式中的n是不带单位的.
应用:已知公式中的任意两个量,可以求第三个量.
.O
1.已知扇形的圆心角为120°,半径为6,则扇形的弧长是( )
A. B. C. D.
解析:根据弧长公式 ,
可得扇形的弧长为 ,故选B
B
练一练
2.已知一条弧的半径为9,弧长为8π,那么这条弧所对的圆心角是为( )
A.200° B.160° C.120° D.80°
B
解析:∵弧长的公式 ,
∴弧长的公式 ,
解得 n=160 ,故选B.
3.已知扇形的圆心角为30°,弧长长为 ,则扇形的半径是( )
A.3cm B.4cm C.5cm D.6cm
D
解析:∵弧长的公式 ,
∴弧长的公式 ,
解得 R=6 ,故选D.
例1 制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(结果取整数).
解:由弧长公式,可得 的长
l (mm)
因此所要求的展直长度
L (mm)
答:管道的展直长度为2970mm.
由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形.
A
B
扇形
A
B
圆心角
半径
半径
弧
扇形的周长:两条半径和弧长.
.O
.O
小试牛刀
下列图形是扇形吗?
.O
.O
.O
.O
.O
.O
弓形
弓形
圆心角占整个周角的
所对扇形面积
思考2:请同学们计算半径为 R,圆心角分别为1800、 900、 10、n0 所对的扇形面积.
圆心角
1800
900
n0
R
·
1°
O
10
R
·
n°
O
R
·
180°
O
R
·
90°
O
圆的面积: S=πR2;圆心角 3600
┐
扇形面积公式
设⊙O半径为R,圆心角为n°的扇形的面积S扇形,则
A
B
n°
注意:
1.扇形面积的大小由圆的半径、圆心角的度数决定.
2.公式中的n是不带单位的.
应用:已知公式中的任意两个量,可以求第三个量.
.O
思考3:扇形的面积公式与弧长公式有联系吗?
如果扇形的半径为R的圆中,圆心角为no ,那么扇形面积的计算公式为:
扇形的弧长与扇形面积的关系为:
应用:已知公式中的任意两个量,可以求第三个量.
1、已知扇形的圆心角为120°,半径为2,则这个
扇形的面积S扇形=____.
2、已知扇形面积为 ,圆心角为60°,则这个
扇形的半径R=____.
3、已知半径为2cm的扇形,其弧长为 cm ,则这
个扇形的面积是_________.
做一做
例2 如图,水平放置的圆柱形排水管道的截面半径是0.6m,其中水面高0.3m,求截面上有水部分的面积S(结果保留小数点后两位).
0
B
A
C
D
S弓形= S扇形OAB-S△OAB
解:连接OA、OB,过圆心O作弦AB的垂直平分线,垂足为D,交 于点C.
∵OC=0.6,DC=0.3
∴OD=OC-DC=0.3
在Rt△OAD中,OA=0.6,OD=0.3
∴∠ OAD=30°, , AB=2AD=0.6
∴∠A OD=60°, ∠ AOB=120°
0
B
A
C
D
有水部分的面积:
答:截面上有水部分的面积为
如图,水平放置的圆柱形排水管道的截面半径是2,其中水面高3,求截面上有水部分的面积.
0
A
B
D
C
E
变式
S弓形= S扇形+S△
注意:
①当弓形面积小于半圆时
S弓形= S扇形-S△
②当弓形面积大于半圆时
S弓形= S扇形+S△
(07年山东)如图,⊙A、⊙B、⊙C、⊙D两两不相交,且半径都是2,求图中阴影部分的面积.
练习
答:图中阴影部分的面积为12π
拓展:如图,在△AOC中,∠AOC=900,∠C=150,以O为圆心,AO为半径的圆交AC与B点,若OA=6,求 的长.
A
C
B
O
解:连接OB
在Rt△AOC中,∠C=150,
∴∠OAB=900-∠C=750
由弧长公式,可得 的长
A
C
B
A′
C′
拓展:如图,把Rt△ABC的斜边放在直线 上,按顺时针方向转动一次,使它转到 的位置.若BC=1,∠A=300.求点A运动到A′位置时,求:(1)点A经过的路线长; (2)边AB扫过的面积;(3)Rt△ABC扫过的面积.
1.弧长和扇形面积公式:
2.扇形定义:由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.
3.弧长和扇形面积的应用:已知公式中的任意两个量,可以求第三个量.
课堂小结
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
