2021秋苏科版八年级数学上册第2章轴对称图形达标检测卷(word版含答案)
文档属性
| 名称 | 2021秋苏科版八年级数学上册第2章轴对称图形达标检测卷(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 401.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-15 09:55:28 | ||
图片预览



文档简介
第2章达标检测卷
一、选择题(每题3分,共24分)
1.下列四个图形中,是轴对称图形的是( )
2.下列图形对称轴最多的是( )
A.正方形 B.等边三角形 C.等腰三角形 D.圆
3.已知一个等腰三角形的一个内角为70°,则另外两个内角的度数是( )
A.55°,55° B.70°,40°
C.55°,55°或70°,40° D.以上都不对
4.如图,B、D、E、C四点共线,且△ABD≌△ACE,若∠AEC=105°,则∠DAE的度数为( )
A.30° B.40° C.50° D.65°
5.在△ABC中,∠A:∠B:∠C=1:2:3,若BC=6,则AB等于( )
A.2 B.3 C.9 D.12
6.如图,在正三角形网格中,已有两个小正三角形被涂灰,再将图中其余小正三角形涂灰一个,使整个被涂灰的图案构成一个轴对称图形的方法有( )
A.1种 B.2种 C.3种 D.6种
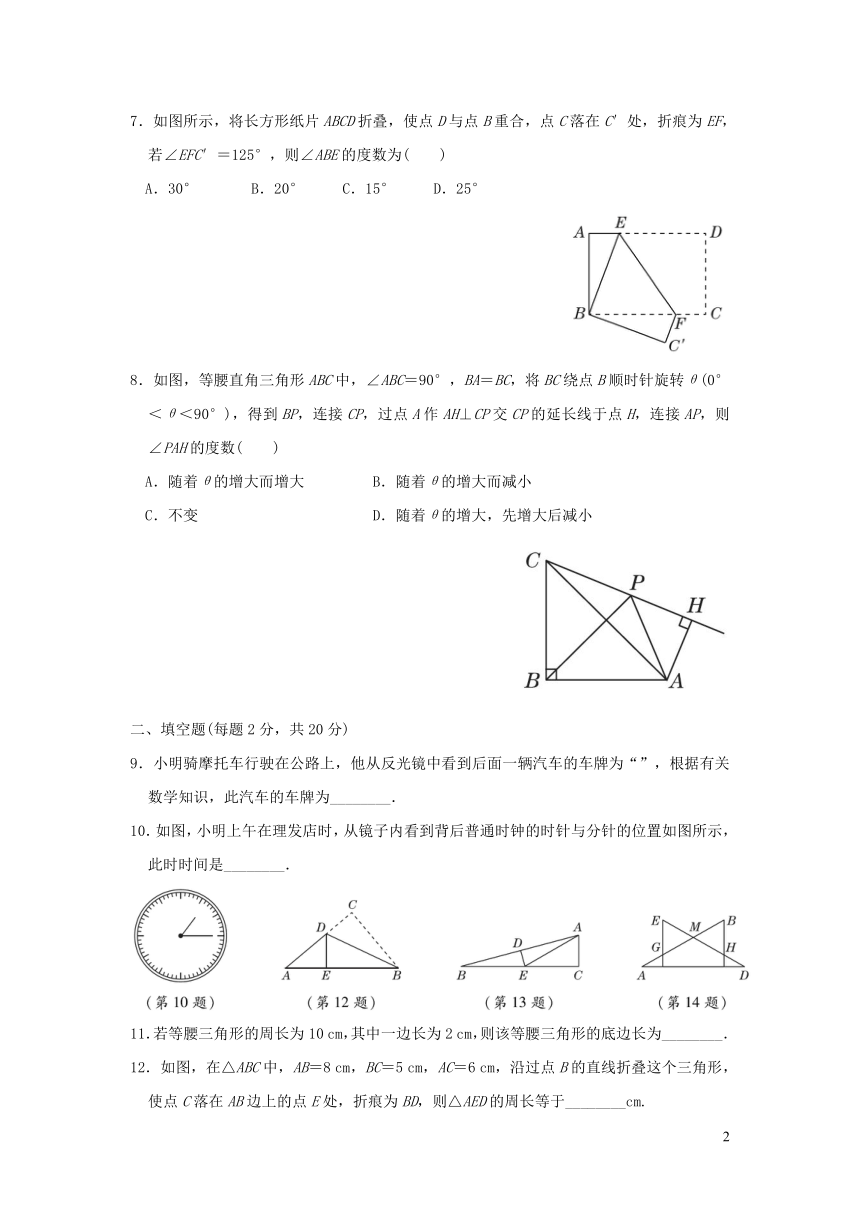
7.如图所示,将长方形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若∠EFC′=125°,则∠ABE的度数为( )
A.30° B.20° C.15° D.25°
8.如图,等腰直角三角形ABC中,∠ABC=90°,BA=BC,将BC绕点B顺时针旋转θ(0°<θ<90°),得到BP,连接CP,过点A作AH⊥CP交CP的延长线于点H,连接AP,则∠PAH的度数( )
A.随着θ的增大而增大 B.随着θ的增大而减小
C.不变 D.随着θ的增大,先增大后减小
二、填空题(每题2分,共20分)
9.小明骑摩托车行驶在公路上,他从反光镜中看到后面一辆汽车的车牌为“”,根据有关数学知识,此汽车的车牌为________.
10.如图,小明上午在理发店时,从镜子内看到背后普通时钟的时针与分针的位置如图所示,此时时间是________.
11.若等腰三角形的周长为10 cm,其中一边长为2 cm,则该等腰三角形的底边长为________.
12.如图,在△ABC中,AB=8 cm,BC=5 cm,AC=6 cm,沿过点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD,则△AED的周长等于________cm.
13.如图,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,BE=4,则AC=________.
14.小明将两个全等且有一个角为60°的直角三角形拼成如图所示的图形,其中两条较长直角边在同一直线上,则图中等腰三角形的个数是________个.
15.如图,在四边形ABCD中,AB=BC=CD=AD,点D到AB的距离为3,∠BAD=60°,点F为AB的中点,点E为AC上的任意一点,则EF+EB的最小值为________.
16.如图,∠ABC,∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于点D,交AC于点E,那么下列结论:①△BDF,△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长为AB+AC;④BD=CE.其中正确的是________.
17.已知C,D两点在线段AB的垂直平分线上,且∠ACB=40°,∠ADB=68°,则∠CAD=________.
18.如图,已知△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=90°,BD,CE交于点F,连接AF.下列结论:①BD=CE;②BF⊥CF;③AF平分∠CAD;④∠AFE=45°.其中正确结论的个数有________个.
三、解答题(19~21题每题6分,22~23题每题7分,24~26题每题8分,共56分)
19.已知a、b、c为△ABC的三边长.b,c满足(b-2)2+|c-3|=0,且a为方程|x-4|=2的解,判断△ABC的形状.
20.两个城镇A,B与两条公路l1,l2的位置如图所示,电信部门需在C处修建一座信号发射塔,要求发射塔到A,B两个城镇的距离必须相等,到l1,l2两条公路的距离也必须相等,那么点C应选在何处?请在图中用尺规作图找出点C.(不写已知、求作、作法,只保留作图痕迹)
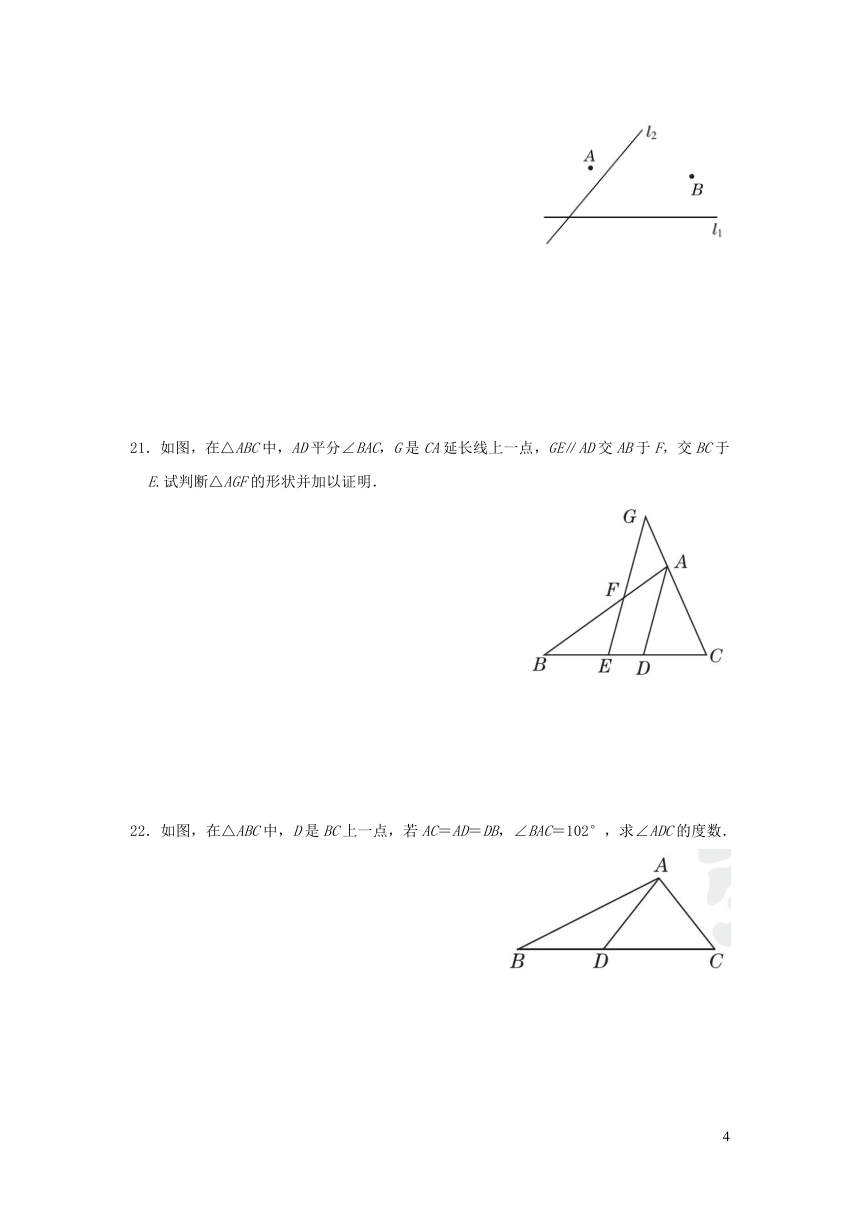
21.如图,在△ABC中,AD平分∠BAC,G是CA延长线上一点,GE∥AD交AB于F,交BC于E.试判断△AGF的形状并加以证明.
22.如图,在△ABC中,D是BC上一点,若AC=AD=DB,∠BAC=102°,求∠ADC的度数.
23.如图,在△ABC中,∠A=40°,∠B=90°,AC的垂直平分线MN分别与AB、AC交于点D、E,求∠BCD的度数.
24.如图,在△ABC中,∠ACB=90°,以AC为边在△ABC外作等边三角形ACD,过点D作AC的垂线,垂足为F,延长DF交AB于点E,连接CE.
(1)求证:AE=CE=BE;
(2)若AB=15 cm,P是直线DE上的一点,则当P在何处时,PB+PC的值最小?求出此时PB+PC的值.
25.如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形,BE交AC于点F,AD交CE于点H,连接FH.
(1)求证:△BCE≌△ACD;
(2)求证:CF=CH;
(3)判断△CFH的形状并说明理由.
26.已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于CE,交CE于点F,交CD于点G(如图①),求证:AE=CG;
(2)直线AH垂直于CE,交CE的延长线于点H,交CD的延长线于点M(如图②),找出图中与BE相等的线段,并说明理由.
答案
一、1.D 2.D 3.C 4.A 5.D
6.C 【点拨】如图,任选标注数字1,2,3的小正三角形涂灰一个,都可以使整个被涂灰的图案构成一个轴对称图形,故选C.
7.B
8.C 【点拨】由旋转得BC=BP=BA,
∴△BCP和△ABP均是等腰三角形.在△BCP中,∠CBP=θ,BC=BP,∴∠BPC=90°-θ.在△ABP中,∠ABP=90°-θ,同理得∠APB=45°+θ,∴∠APC=∠BPC +∠APB =135°,∴∠APH=45°,又∵∠AHC=90°,∴∠PAH=45°,即其度数是个定值,不变.
二、9.浙B63859 10.10:45
11.2 cm 12.9 13.2 14.3
15.3 【点拨】如图,连接BD.∵AB=BC=CD=AD,∴易得AC垂直平分BD,∴点B关于直线AC的对称点为点D.连接DF,则DF的长即为EF+EB的最小值.在△ABD中,由∠BAD=60°,AD=AB,可得△ABD为等边三角形.∵点F为AB的中点,∴DF⊥AB.∴DF=3.故EF+EB的最小值为3.
16.①②③
17.126°或14°
18.3 【点拨】易知△ABC和△ADE都是等腰直角三角形,∴AB=AC,AD=AE.
∵∠BAD=90°+∠CAD,∠CAE=90°+∠CAD,∴∠BAD=∠CAE.
在△AEC与△ADB中,
∴△AEC≌△ADB(SAS),
∴BD=CE,
∠ADB=∠AEC.
∵∠DEF+∠AEC+∠EDA=90°,
∴∠DEF+∠ADB+∠EDA=90°.
∴∠DEF+∠EDF=90°,
∴BD⊥CE,即BF⊥CF.
作AN⊥CE,AM⊥BD.
易得AM=AN,
∴FA平分∠BFE,
∴∠AFE=45°.
若③成立,则∠EAF=∠BAF,
∵∠AFE=∠AFB,
∴∠AEF=∠ABD=∠ADB,
∴AB=AD,由题知,AB不一定等于AD.
综上①②④正确,③错误.
三、19.解:∵(b-2)2+|c-3|=0,
∴b-2=0,c-3=0,
解得b=2,c=3.
∵a为方程|x-4|=2的解,
∴a-4=±2,
解得a=6或2.
∵a、b、c为△ABC的三边长,b+c<6,
∴a=6不合题意,舍去,
∴a=2,
∴a=b=2,
∴△ABC是等腰三角形.
20.解:点C的位置如图所示.
21.解:△AGF是等腰三角形.
证明:∵AD平分∠BAC,
∴∠BAD=∠DAC.
∵GE∥AD,
∴∠G=∠DAC,∠GFA=∠FAD.∴∠G=∠GFA.
∴AF=GA.
∴△AGF是等腰三角形.
22.解:∵AC=AD=DB,
∴∠B=∠BAD,∠ADC=∠C.
设∠B=∠BAD=x°,
则∠ADC=2x°,∴∠C=2x°,
∴∠B+∠C=3x°.
∵∠BAC=102°,
∴∠B+∠C=78°,
∴3x=78,解得x=26.
∴∠ADC=52°.
23.解:∵∠B=90°,∠A=40°,∴∠ACB=50°.
∵MN是线段AC的垂直平分线.
∴AE=CE.
在△ADE和△CDE中,
∴△ADE≌△CDE(SAS),
∴∠DCA=∠A=40°.
∴∠BCD=∠ACB-∠DCA=50°-40°=10°.
24.(1)证明:∵△ACD为等边三角形,DE⊥AC,
∴DE垂直平分AC,∴AE=CE.
∴∠AEF=∠FEC.
∵∠ACB=∠AFE=90°,
∴DE∥BC.
∴∠AEF=∠EBC,∠FEC=∠ECB.
∴∠ECB=∠EBC.
∴CE=BE.∴AE=CE=BE.
(2)解:连接PA,PC.∵DE垂直平分AC,P在DE 上,∴PC=PA.∵两点之间线段最短,∴当P与E重合时,PB+PC=PA+PB=AB,此时PB+PC最小,为15 cm.
25.(1)证明:∵△ABC和△CDE都是等边三角形,∴BC=AC,CE=CD,
∠ACB=∠ECD=60°,
∴∠BCE=60°+∠ACE=∠ACD,
∴△BCE≌△ACD(SAS).
(2)证明:∵△BCE≌△ACD,∴∠FBC=∠HAC.∵∠ACB=∠ECD=60°,∴∠FCH=180°-∠ACB-∠ECD=60°,∴∠BCF=∠ACH.又∵BC=AC,
∴△BCF≌△ACH(ASA),∴CF=CH.
(3)解:△CFH是等边三角形.
理由:∵CF=CH,∠FCH=60°,
∴△CFH是等边三角形.
26.(1)证明:∵点D是AB的中点,AC=BC,∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,∠CAD=∠CBD=45°,
∴∠CAE=∠BCG.又∵BF⊥CE,
∴∠CBG+∠BCF=90°.
又∵∠ACE+∠BCF=90°,
∴∠ACE=∠CBG,
∴△AEC≌△CGB(ASA),
∴AE=CG.
(2)解:BE=CM.
理由:∵CH⊥HM,CD⊥ED,
∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,
∴∠CMA=∠BEC.
又∵CA=BC,∠ACM=∠CBE=45°,
∴△BCE≌△CAM,∴BE=CM.
1
一、选择题(每题3分,共24分)
1.下列四个图形中,是轴对称图形的是( )
2.下列图形对称轴最多的是( )
A.正方形 B.等边三角形 C.等腰三角形 D.圆
3.已知一个等腰三角形的一个内角为70°,则另外两个内角的度数是( )
A.55°,55° B.70°,40°
C.55°,55°或70°,40° D.以上都不对
4.如图,B、D、E、C四点共线,且△ABD≌△ACE,若∠AEC=105°,则∠DAE的度数为( )
A.30° B.40° C.50° D.65°
5.在△ABC中,∠A:∠B:∠C=1:2:3,若BC=6,则AB等于( )
A.2 B.3 C.9 D.12
6.如图,在正三角形网格中,已有两个小正三角形被涂灰,再将图中其余小正三角形涂灰一个,使整个被涂灰的图案构成一个轴对称图形的方法有( )
A.1种 B.2种 C.3种 D.6种
7.如图所示,将长方形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若∠EFC′=125°,则∠ABE的度数为( )
A.30° B.20° C.15° D.25°
8.如图,等腰直角三角形ABC中,∠ABC=90°,BA=BC,将BC绕点B顺时针旋转θ(0°<θ<90°),得到BP,连接CP,过点A作AH⊥CP交CP的延长线于点H,连接AP,则∠PAH的度数( )
A.随着θ的增大而增大 B.随着θ的增大而减小
C.不变 D.随着θ的增大,先增大后减小
二、填空题(每题2分,共20分)
9.小明骑摩托车行驶在公路上,他从反光镜中看到后面一辆汽车的车牌为“”,根据有关数学知识,此汽车的车牌为________.
10.如图,小明上午在理发店时,从镜子内看到背后普通时钟的时针与分针的位置如图所示,此时时间是________.
11.若等腰三角形的周长为10 cm,其中一边长为2 cm,则该等腰三角形的底边长为________.
12.如图,在△ABC中,AB=8 cm,BC=5 cm,AC=6 cm,沿过点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD,则△AED的周长等于________cm.
13.如图,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,BE=4,则AC=________.
14.小明将两个全等且有一个角为60°的直角三角形拼成如图所示的图形,其中两条较长直角边在同一直线上,则图中等腰三角形的个数是________个.
15.如图,在四边形ABCD中,AB=BC=CD=AD,点D到AB的距离为3,∠BAD=60°,点F为AB的中点,点E为AC上的任意一点,则EF+EB的最小值为________.
16.如图,∠ABC,∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于点D,交AC于点E,那么下列结论:①△BDF,△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长为AB+AC;④BD=CE.其中正确的是________.
17.已知C,D两点在线段AB的垂直平分线上,且∠ACB=40°,∠ADB=68°,则∠CAD=________.
18.如图,已知△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=90°,BD,CE交于点F,连接AF.下列结论:①BD=CE;②BF⊥CF;③AF平分∠CAD;④∠AFE=45°.其中正确结论的个数有________个.
三、解答题(19~21题每题6分,22~23题每题7分,24~26题每题8分,共56分)
19.已知a、b、c为△ABC的三边长.b,c满足(b-2)2+|c-3|=0,且a为方程|x-4|=2的解,判断△ABC的形状.
20.两个城镇A,B与两条公路l1,l2的位置如图所示,电信部门需在C处修建一座信号发射塔,要求发射塔到A,B两个城镇的距离必须相等,到l1,l2两条公路的距离也必须相等,那么点C应选在何处?请在图中用尺规作图找出点C.(不写已知、求作、作法,只保留作图痕迹)
21.如图,在△ABC中,AD平分∠BAC,G是CA延长线上一点,GE∥AD交AB于F,交BC于E.试判断△AGF的形状并加以证明.
22.如图,在△ABC中,D是BC上一点,若AC=AD=DB,∠BAC=102°,求∠ADC的度数.
23.如图,在△ABC中,∠A=40°,∠B=90°,AC的垂直平分线MN分别与AB、AC交于点D、E,求∠BCD的度数.
24.如图,在△ABC中,∠ACB=90°,以AC为边在△ABC外作等边三角形ACD,过点D作AC的垂线,垂足为F,延长DF交AB于点E,连接CE.
(1)求证:AE=CE=BE;
(2)若AB=15 cm,P是直线DE上的一点,则当P在何处时,PB+PC的值最小?求出此时PB+PC的值.
25.如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形,BE交AC于点F,AD交CE于点H,连接FH.
(1)求证:△BCE≌△ACD;
(2)求证:CF=CH;
(3)判断△CFH的形状并说明理由.
26.已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于CE,交CE于点F,交CD于点G(如图①),求证:AE=CG;
(2)直线AH垂直于CE,交CE的延长线于点H,交CD的延长线于点M(如图②),找出图中与BE相等的线段,并说明理由.
答案
一、1.D 2.D 3.C 4.A 5.D
6.C 【点拨】如图,任选标注数字1,2,3的小正三角形涂灰一个,都可以使整个被涂灰的图案构成一个轴对称图形,故选C.
7.B
8.C 【点拨】由旋转得BC=BP=BA,
∴△BCP和△ABP均是等腰三角形.在△BCP中,∠CBP=θ,BC=BP,∴∠BPC=90°-θ.在△ABP中,∠ABP=90°-θ,同理得∠APB=45°+θ,∴∠APC=∠BPC +∠APB =135°,∴∠APH=45°,又∵∠AHC=90°,∴∠PAH=45°,即其度数是个定值,不变.
二、9.浙B63859 10.10:45
11.2 cm 12.9 13.2 14.3
15.3 【点拨】如图,连接BD.∵AB=BC=CD=AD,∴易得AC垂直平分BD,∴点B关于直线AC的对称点为点D.连接DF,则DF的长即为EF+EB的最小值.在△ABD中,由∠BAD=60°,AD=AB,可得△ABD为等边三角形.∵点F为AB的中点,∴DF⊥AB.∴DF=3.故EF+EB的最小值为3.
16.①②③
17.126°或14°
18.3 【点拨】易知△ABC和△ADE都是等腰直角三角形,∴AB=AC,AD=AE.
∵∠BAD=90°+∠CAD,∠CAE=90°+∠CAD,∴∠BAD=∠CAE.
在△AEC与△ADB中,
∴△AEC≌△ADB(SAS),
∴BD=CE,
∠ADB=∠AEC.
∵∠DEF+∠AEC+∠EDA=90°,
∴∠DEF+∠ADB+∠EDA=90°.
∴∠DEF+∠EDF=90°,
∴BD⊥CE,即BF⊥CF.
作AN⊥CE,AM⊥BD.
易得AM=AN,
∴FA平分∠BFE,
∴∠AFE=45°.
若③成立,则∠EAF=∠BAF,
∵∠AFE=∠AFB,
∴∠AEF=∠ABD=∠ADB,
∴AB=AD,由题知,AB不一定等于AD.
综上①②④正确,③错误.
三、19.解:∵(b-2)2+|c-3|=0,
∴b-2=0,c-3=0,
解得b=2,c=3.
∵a为方程|x-4|=2的解,
∴a-4=±2,
解得a=6或2.
∵a、b、c为△ABC的三边长,b+c<6,
∴a=6不合题意,舍去,
∴a=2,
∴a=b=2,
∴△ABC是等腰三角形.
20.解:点C的位置如图所示.
21.解:△AGF是等腰三角形.
证明:∵AD平分∠BAC,
∴∠BAD=∠DAC.
∵GE∥AD,
∴∠G=∠DAC,∠GFA=∠FAD.∴∠G=∠GFA.
∴AF=GA.
∴△AGF是等腰三角形.
22.解:∵AC=AD=DB,
∴∠B=∠BAD,∠ADC=∠C.
设∠B=∠BAD=x°,
则∠ADC=2x°,∴∠C=2x°,
∴∠B+∠C=3x°.
∵∠BAC=102°,
∴∠B+∠C=78°,
∴3x=78,解得x=26.
∴∠ADC=52°.
23.解:∵∠B=90°,∠A=40°,∴∠ACB=50°.
∵MN是线段AC的垂直平分线.
∴AE=CE.
在△ADE和△CDE中,
∴△ADE≌△CDE(SAS),
∴∠DCA=∠A=40°.
∴∠BCD=∠ACB-∠DCA=50°-40°=10°.
24.(1)证明:∵△ACD为等边三角形,DE⊥AC,
∴DE垂直平分AC,∴AE=CE.
∴∠AEF=∠FEC.
∵∠ACB=∠AFE=90°,
∴DE∥BC.
∴∠AEF=∠EBC,∠FEC=∠ECB.
∴∠ECB=∠EBC.
∴CE=BE.∴AE=CE=BE.
(2)解:连接PA,PC.∵DE垂直平分AC,P在DE 上,∴PC=PA.∵两点之间线段最短,∴当P与E重合时,PB+PC=PA+PB=AB,此时PB+PC最小,为15 cm.
25.(1)证明:∵△ABC和△CDE都是等边三角形,∴BC=AC,CE=CD,
∠ACB=∠ECD=60°,
∴∠BCE=60°+∠ACE=∠ACD,
∴△BCE≌△ACD(SAS).
(2)证明:∵△BCE≌△ACD,∴∠FBC=∠HAC.∵∠ACB=∠ECD=60°,∴∠FCH=180°-∠ACB-∠ECD=60°,∴∠BCF=∠ACH.又∵BC=AC,
∴△BCF≌△ACH(ASA),∴CF=CH.
(3)解:△CFH是等边三角形.
理由:∵CF=CH,∠FCH=60°,
∴△CFH是等边三角形.
26.(1)证明:∵点D是AB的中点,AC=BC,∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,∠CAD=∠CBD=45°,
∴∠CAE=∠BCG.又∵BF⊥CE,
∴∠CBG+∠BCF=90°.
又∵∠ACE+∠BCF=90°,
∴∠ACE=∠CBG,
∴△AEC≌△CGB(ASA),
∴AE=CG.
(2)解:BE=CM.
理由:∵CH⊥HM,CD⊥ED,
∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,
∴∠CMA=∠BEC.
又∵CA=BC,∠ACM=∠CBE=45°,
∴△BCE≌△CAM,∴BE=CM.
1
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
