第二章 一元二次方程单元检测卷(含解析)
文档属性
| 名称 | 第二章 一元二次方程单元检测卷(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-14 20:20:38 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第二章《一元二次方程》检测卷
第I卷(选择题)
一、选择题(每小题3分,共30分)
1.下列方程中一元二次方程的个数为( )
①;②;③;④.
A.1个 B.2个 C.3个 D.4个
2.用配方法解一元二次方程,下列变形正确的的是( )
A. B.
C. D.
3.已知关于x的一元二次方程有两个不相等的实数根,则m的取值范围是 ( )
A.m≥2 B.m<2 C.m≥0 D.m<0
4.如图,一农户要建一个矩形花圃,花圃的一边利用长为12m的住房墙,另外三边用25m长的篱笆围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门,花圃面积为80m2,设与墙垂直的一边长为xm(已标注在图中),则可以列出关于x的方程是( )
A.x(26﹣2x)=80 B.x(24﹣2x)=80
C.(x﹣1)(26﹣2x)=80 D.x(25﹣2x)=80
5.观察下列表格,可以作为一元二次方程的一个近似解的为( )
A. B. C. D.
6.已知:毕业典礼后,小芳学习小组内部的名同学,每两个同学都互相交换了礼物,她们一共买了份礼物.根据以上条件可以列出以下哪个方程( )
A. B.
C. D.
7.设a,b是方程的两个实数根,则的值为( )
A.2018 B.2020 C.2021 D.2024
8.定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.如图,在平面直角坐标系xOy中,矩形OABC的边OA=3,OC=4,点M(2,0),在边AB存在点P,使得△CMP为“智慧三角形”,则点P的坐标为( )
A.(3,1)或(3,3) B.(3,)或(3,3)
C.(3,)或(3,1) D.(3,)或(3,1)或(3,3)
9.若一元二次方程无实数根,则一次函数的图像经过第( )
A.二、三、四象限 B.一、三、四象限 C.一、二、四象限 D.一、二、三象限
10.对于一元二次方程,下列说法:
①若,则;
②若方程有两个不相等的实根,则方程必有两个不相等的实根;
③若是方程的一个根,则一定有成立;
④若是一元二次方程的根,则.
其中正确的有( )
A.个 B.个 C.个 D.个
第II卷(非选择题)
二、填空题(每小题4分,共28分)
11.方程的解是______.
12.已知、是一元二次方程的两个实数根,则的值是_____.
13.已知两直角边的长度恰好是一元二次方程的两个实数根,那么的面积是______.
14.关于x的方程是,那么当m___________时,方程为一元二次方程.
15.一元二次方程有一根为,则另一个根为__________.
16.若,则的值为__________.
17.有一张长40cm,宽30cm的长方形硬纸片(如图1),截去四个全等的小正方形之后,折成无盖的纸盒(如图2).若纸盒的底面积为600cm2,则纸盒的高为__________.
三、解答题(一)(每小题6分,共18分)
18.解一元二次方程:
(1)
(2)
19.求证:不论k取何实数,方程都没有实根.
20.某地区2019年投入教育经费2000万元,2021年投入教育经费2880万元.
(1)求2019年至2021年该地区投入教育经费的年平均增长率;
(2)根据(1)所得的年平均增长率,预计2022年该地区将投入教育经费多少万元.
四、解答题(二)(每小题8分,共24分)
21.已知关于x的一元二次方程有两个不相等的实数根.
(1)求实数k的取值范围;
(2)设方程两个实数根分别为,,且满足,求k的值.
22.如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.若P,Q两点同时出发,当点Q运动到点C时,P,Q两点同时停止运动.求:
(1)几秒后,PQ的长度等于2cm?
(2)△PBQ的面积能否等于7cm2?说明理由.
23.端年节吃粽子是中国古老的传统习俗,某粽子批发店卖出每个粽子的利润为2元,根据员工情况,每天最多能做1100个,由市场调查得知,若每个粽子的单价降低x元,则粽子每天的销售量y(个)关于x(元)的函数关系式为y=800x+400.
(1)若每个粽子降价0.2元,则该店每天的销售量为 个,每天的总利润为 元.
(2)当每个粽子的单价降低多少元时,该店每天的总利润刚好是1200元?
五、解答题(三)(每小题10分,共20分)
24.先阅读理解下面的例题,再按要求解答下列问题:
例题:求代数式的最小值.
解:
,
∵,
∴,
∴的最小值是4.
(1)代数式的最小值为___________;
(2)求代数式的最小值.
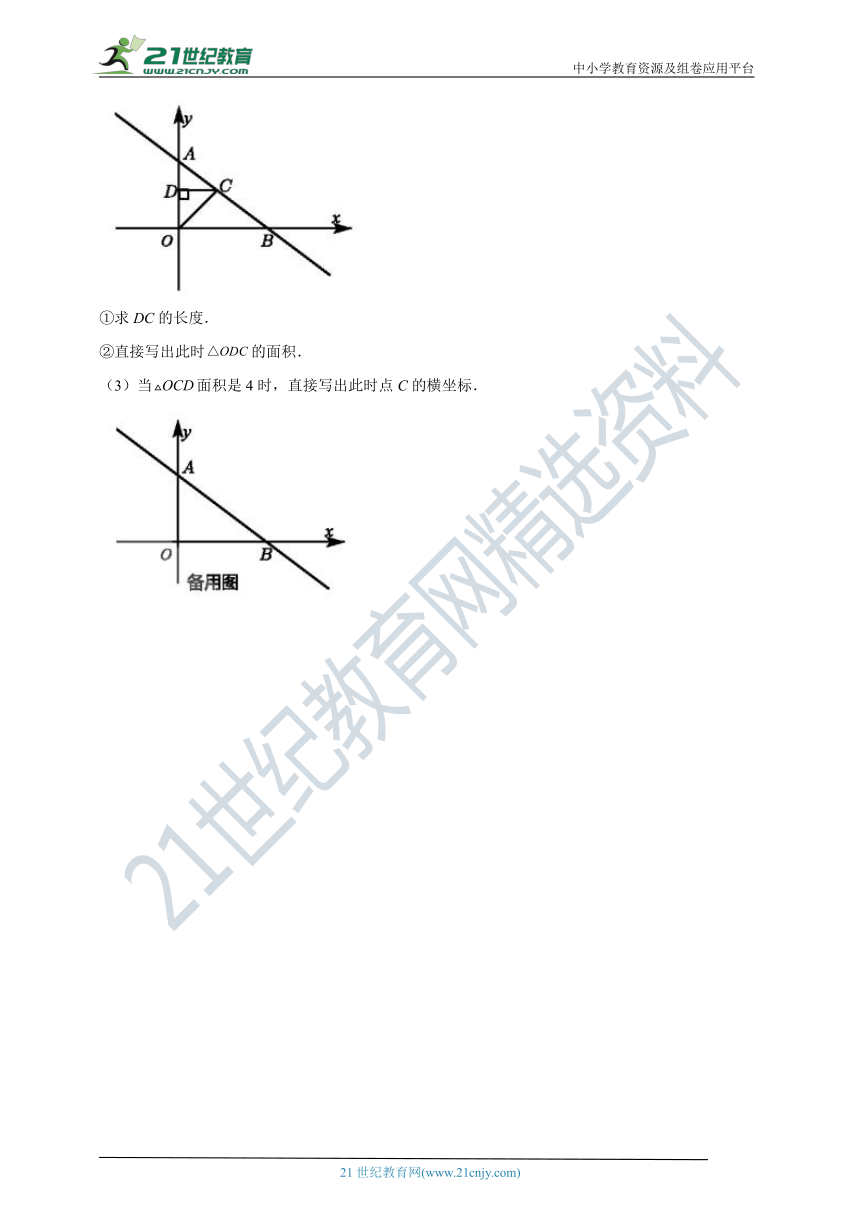
25.在平面直角坐标系中,点O为坐标原点,直线AB与y轴、x轴分别相交于点A,点B,A点坐标为,B点坐标为,点C在直线AB上,过点C作轴,垂足为点D,连接OC,
(1)求直线AB的解析式.
(2)如图,点C在线段AB上,当时.
①求DC的长度.
②直接写出此时的面积.
(3)当面积是4时,直接写出此时点C的横坐标.
第二章《一元二次方程》检测卷
第I卷(选择题)
一、选择题(每小题3分,共30分)
1.下列方程中一元二次方程的个数为( )
①;②;③;④.
A.1个 B.2个 C.3个 D.4个
【答案】A
【分析】
根据一元二次方程的定义直接判断即可.
【详解】
解:是一元二次方程;
含有两个未知数,不是一元二次方程;
未知数在根号内,不是一元二次方程;
未知数在分母中,不是一元二次方程;
故选:A.
【点睛】
本题考查了一元二次方程的定义,明确只含有一个未知数,未知数的最高次为2次的整式方程是一元二次方程是解题关键.
2.用配方法解一元二次方程,下列变形正确的的是( )
A. B.
C. D.
【答案】D
【分析】
根据完全平方式的特点,先移项,再两边加一次项系数一半的平方.
【详解】
解:,
∴,
∴.
故选:D.
【点睛】
本题考查了解一元二次方程-配方法:将一元二次方程配成(x+m)2=n的形式,再利用直接开平方法求解,这种解一元二次方程的方法叫配方法.
3.已知关于x的一元二次方程有两个不相等的实数根,则m的取值范围是 ( )
A.m≥2 B.m<2 C.m≥0 D.m<0
【答案】B
【分析】
根据根的判别式,可知Δ>0,据此即可求出m的取值范围.
【详解】
解:∵关于x的一元二次方程有两个不相等的实数根,
∴
Δ=,
解得:m<2,
故选:B
【点睛】
此题考查了根的判别式,解题时要注意一元二次方程成立的条件:二次项系数不为0
4.如图,一农户要建一个矩形花圃,花圃的一边利用长为12m的住房墙,另外三边用25m长的篱笆围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门,花圃面积为80m2,设与墙垂直的一边长为xm(已标注在图中),则可以列出关于x的方程是( )
A.x(26﹣2x)=80 B.x(24﹣2x)=80
C.(x﹣1)(26﹣2x)=80 D.x(25﹣2x)=80
【答案】A
【分析】
设与墙垂直的一边长为xm,则与墙平行的一边长为(26﹣2x)m,根据花圃面积为80m2即可列出关于x的一元二次方程,此题得解.
【详解】
解:设与墙垂直的一边长为xm,则与墙平行的一边长为(26﹣2x)m,
根据题意得:x(26﹣2x)=80.
故选:A.
【点睛】
本题主要考查了一元二次方程的应用,明确题意,准确找到等量关系是解题的关键.
5.观察下列表格,可以作为一元二次方程的一个近似解的为( )
A. B. C. D.
【答案】B
【分析】
根据表格中的数据,可判断代数式的值为4.61和4.56时,对应的值为-1.12和-1.11,观察原方程可理解为求代数式的值为4.6时,对应的的值范围,由此判断即可.
【详解】
解:∵时,;时,;
∴时,对应应满足,
∵-1.123<-1.12<-1.117<-1.11<-1.089<-1.073
∴原方程的近似解为:-1.117,
故选:B.
【点睛】
本题考查一元二次方程的近似解,理解表格中的数据,掌握求近似解的方法先求x的范围,再比较大小选取是解题关键.
6.已知:毕业典礼后,小芳学习小组内部的名同学,每两个同学都互相交换了礼物,她们一共买了份礼物.根据以上条件可以列出以下哪个方程( )
A. B.
C. D.
【答案】C
【分析】
根据每两名同学之间交换礼物一个,则m人共赠贺卡m(m-1)张,列方程即可.
【详解】
解:根据题意,得
m(m-1)=20,
故选C.
【点睛】
此题主要考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.
7.设a,b是方程的两个实数根,则的值为( )
A.2018 B.2020 C.2021 D.2024
【答案】A
【分析】
根据根与系数的关系和一元二次方程的解得出,,将变形后代入,即可求出答案.
【详解】
解:∵a,b是方程的两个实数根,
∴,
∴.
故选:A.
【点睛】
本题考查了根与系数的关系和一元二次方程的解,能求出和是解此题的关键.
8.定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.如图,在平面直角坐标系xOy中,矩形OABC的边OA=3,OC=4,点M(2,0),在边AB存在点P,使得△CMP为“智慧三角形”,则点P的坐标为( )
A.(3,1)或(3,3) B.(3,)或(3,3)
C.(3,)或(3,1) D.(3,)或(3,1)或(3,3)
【答案】D
【分析】
由题意可知,“智慧三角形”是直角三角形,∠CPM=90°或∠CMP=90°,设P(3,a),则AP=a,BP=4 a;分两种情况:①若∠CPM=90°,②若∠CMP=90°,根据勾股定理分别求出CP2、MP2、CM2,并根据图形列出关于a的方程,解得a的值,则可得答案.
【详解】
解:由题意可知,“智慧三角形”是直角三角形,∠CPM=90°或∠CMP=90°,
∴设P(3,a),则AP=a,BP=4 a;
①若∠CPM=90°,在Rt△BCP中,由勾股定理得:
CP2=BP2+BC2=(4 a)2+9,
在Rt△MPA中,由勾股定理得:
MP2=MA2+AP2=1+a2,
在Rt△MPC中,由勾股定理得:
CM2=MP2+CP2=1+a2+(4 a)2+9=2a2 8a+26,
又∵CM2=OM2+OC2=4+16=20,
∴2a2 8a+26=20,
∴(a 3)(a 1)=0,
解得:a=3或a=1,
∴P(3,3)或(3,1);
②若∠CMP=90°,在Rt△BCP中,由勾股定理得:
CP2=BP2+BC2=(4 a)2+9,
在Rt△MPA中,由勾股定理得:
MP2=MA2+AP2=1+a2,
∵CM2=OM2+OC2=20,
在Rt△MCP中,由勾股定理得:
CM2+MP2=CP2,
∴20+1+a2=(4 a)2+9,
解得:a=.
∴P(3,).
综上,P(3,)或(3,1)或(3,3).
故选:D.
【点睛】
本题考查了矩形的性质及勾股定理在几何图形坐标计算中的应用,数形结合、分类讨论并根据题意正确地列式是解题的关键.
9.若一元二次方程无实数根,则一次函数的图像经过第( )
A.二、三、四象限 B.一、三、四象限 C.一、二、四象限 D.一、二、三象限
【答案】A
【分析】
先根据一元二次方程无实数根,利用判别式求出m的取值范围,然后判断一次函数经过的象限即可.
【详解】
解:由已知得:,
解得,
∵一次函数中,,
∴该一次函数图像在第二、三、四象限,
故选A.
【点睛】
本题主要考查了一元二次方程根的判别式,根据函数解析式判断函数经过的象限,解题的关键在于能够熟练掌握一元二次方程根的判别式.
10.对于一元二次方程,下列说法:
①若,则;
②若方程有两个不相等的实根,则方程必有两个不相等的实根;
③若是方程的一个根,则一定有成立;
④若是一元二次方程的根,则.
其中正确的有( )
A.个 B.个 C.个 D.个
【答案】C
【分析】
按照方程的解的含义、一元二次方程的实数根与判别式的关系、等式的性质、一元二次方程的求根公式等对各选项分别讨论,可得答案.
【详解】
解:①若a+b+c=0,则x=1是方程ax2+bx+c=0的解,
由一元二次方程的实数根与判别式的关系可知:Δ=b2-4ac≥0,故①正确;
②方程ax2+c=0有两个不相等的实根,
∴Δ=0-4ac>0,
∴-4ac>0
则方程ax2+bx+c=0的判别式Δ=b2-4ac>0,
∴方程ax2+bx+c=0必有两个不相等的实根,故②正确;
③∵c是方程ax2+bx+c=0的一个根,
则ac2+bc+c=0,
∴c(ac+b+1)=0,
若c=0,等式仍然成立,
但ac+b+1=0不一定成立,故③不正确;
④若x0是一元二次方程ax2+bx+c=0的根,
则由求根公式可得:x0=,
∴2ax0+b=±,
∴b2-4ac=(2ax0+b)2,故④正确.
故正确的有①②④,
故选:C.
【点睛】
本题考查一元二次方程根的判断,根据方程形式,判断根的情况是求解本题的关键.
第II卷(非选择题)
二、填空题(每小题4分,共28分)
11.方程的解是______.
【答案】,
【分析】
先移项,使方程右边为0,再提公因式,然后根据“两式相乘值为0,这两式中至少有一式值为0”进行求解.
【详解】
解:原方程可化为:,
因式分解得:,
所以或,
解得:,,
故答案为:,.
【点睛】
本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.本题运用的是因式分解法.
12.已知、是一元二次方程的两个实数根,则的值是_____.
【答案】
【分析】
根据一元二次方程的根与系数的关系计算.
【详解】
解:由题意可得:,
∴=,
故答案为:.
【点睛】
此题考查一元二次方程的根与系数的关系,熟记根与系数的关系是解题的关键.
13.已知两直角边的长度恰好是一元二次方程的两个实数根,那么的面积是______.
【答案】6
【分析】
设两直角边的长度分别为,n,则,n是方程的两个实数根,再利用一元二次方程的根与系数的关系即可求得答案.
【详解】
解:设两直角边的长度分别为,n,
由题意可得:,n是方程的两个实数根,
∴,
∴,
故答案为:6.
【点睛】
本题考查了一元二次方程的根与系数的关系,若,是一元二次方程的两根时,则,,熟练掌握根与系数的关系是解决本题的关键.
14.关于x的方程是,那么当m___________时,方程为一元二次方程.
【答案】≠±1
【分析】
由一元二次方程的二次项系数不能是0,可以确定m的取值
【详解】
解:若方程是一元二次方程,则:m2 1≠0,
∴m≠±1,
故答案是:≠±1.
【点睛】
本题考查的是一元二次方程的定义:含有一个未知数,并且未知数的最高次数是2的整式方程是一元二次方程,掌握一元二次方程的定义是解题的关键.
15.一元二次方程有一根为,则另一个根为__________.
【答案】
【分析】
根据一元二次方程的根与系数的关系来求方程的另一个根.
【详解】
解:设是关于x的一元二次方程的两个根.
由韦达定理,得,即,
解得,,
即方程的另一个根为1.
故答案为:1.
【点睛】
本题考查了根与系数的关系,在利用根与系数的关系时,要注意等式中的a、b、c所表示的含义.
16.若,则的值为__________.
【答案】-4或2
【分析】
先用换元法把方程转化为一元二次方程,再利用十字相乘法因式分解的形式,即可求解.
【详解】
解:2x+3y=t,原方程可变形为:t2+2t-8=0,
∴(t+4)(t-2)=0,
解得,t=-4或2;
∴2x+3y的值为-4或2.
故答案为:-4或2.
【点睛】
本题考查了一元二次方程的解法和换元法的运用,解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.
17.有一张长40cm,宽30cm的长方形硬纸片(如图1),截去四个全等的小正方形之后,折成无盖的纸盒(如图2).若纸盒的底面积为600cm2,则纸盒的高为__________.
【答案】5cm
【分析】
设纸盒的高是,根据题意,其底面的长宽分别为(40-2x)cm和(30-2x)cm,根据长方形面积公式列方程求解即可.
【详解】
解:设纸盒的高是.
依题意,得.
整理得.
解得,(不合题意,舍去).
答:纸盒的高为.
【点睛】
本题考查一元二次方程的应用,根据题意用含x的式子表示底面的长和宽,正确列方程,解方程是本题的解题关键.
三、解答题(一)(每小题6分,共18分)
18.解一元二次方程:
(1)
(2)
【答案】(1),;(2),
【分析】
(1)根据一元二次方程的求根公式即可求解;
(2)利用因式分解法求解一元二次方程即可.
【详解】
(1).
解:,,,
,
.
,.
(2)解:
或
,.
【点睛】
此题主要考查一元二次方程的求解,解题的关键是熟知公式法及因式分解法的运用.
19.求证:不论k取何实数,方程都没有实根.
【答案】见解析
【分析】
先根据得到即可得到方程是一元二次方程,然后利用一元二次方程根的判别式进行求解即可.
【详解】
解:∵,
∴,
∴方程是一元二次方程,
∴
,
∵,
∴,
∴,即恒成立,
∴方程都没有实根.
【点睛】
本题主要考查了一元二次方程根的判别式,完全平方公式,解题的关键在于能够熟练掌握相关知识进行求解.
20.某地区2019年投入教育经费2000万元,2021年投入教育经费2880万元.
(1)求2019年至2021年该地区投入教育经费的年平均增长率;
(2)根据(1)所得的年平均增长率,预计2022年该地区将投入教育经费多少万元.
【答案】(1)2019年至2021年该地区投入教育经费的年平均增长率为20%,(2) 2022年该地区将投入教育经费3456万元.
【分析】
(1)设年平均增长率为x,一般用增长后的量=增长前的量×(1+增长率),2019年投入教育经费是2000万元,2020年在2019年的基础上增长x,就是2019年的教育经费数额的倍,2021年在2020年的基础上再增长x,2020年的教育经费数额为2000,即可列出方程求解;
(2)利用(1)中求得的增长率来求2022年该地区将投入教育经费.
【详解】
解:(1)设年平均增长率为x,由题意得:
2000×(1+x)2=2880,
解得:x1=0.2, x2=-2.2(舍去),
答2019年至2021年该地区投入教育经费的年平均增长率为20%;
(2) 2880×(1+20%)=3456(万元),
答:2022年该地区将投入教育经费3456万元.
【点睛】
本题考查了一元二次方程中增长率的知识.掌握增长前的量×(1+年平均增长率) =增长后的量是本题的关键.
四、解答题(二)(每小题8分,共24分)
21.已知关于x的一元二次方程有两个不相等的实数根.
(1)求实数k的取值范围;
(2)设方程两个实数根分别为,,且满足,求k的值.
【答案】(1)且;(2).
【分析】
(1)根据一元二次方程根的判别式和一元二次方程的定义求解即可;
(2)根据一元二次方程根与系数的关系求解即可.
【详解】
解:(1)∵方程有两个不相等的实数根,
∴且,即且,
解得且;
(2)由根与系数的关系可得,,
由题意可得,即,
∴
解得或,
经检验可知:,都是原分式方程的解.
由(1)可知且
∴.
【点睛】
本题主要考查了解分式方程,解一元二次方程,一元二次方程的定义,一元二次方程根与系数的关系,解题的关键在于能够熟练掌握相关知识进行求解.
22.如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.若P,Q两点同时出发,当点Q运动到点C时,P,Q两点同时停止运动.求:
(1)几秒后,PQ的长度等于2cm?
(2)△PBQ的面积能否等于7cm2?说明理由.
【答案】(1)3;(2)不能,理由见解析
【分析】
(1)根据题意,设运动时间为秒,进而分别写出的长,进而根据勾股定理列出方程即可;
(2)根据题意列出方程,根据根的判别式进行判断即可
【详解】
(1)设经过秒后,PQ的长度等于2cm,依题意得,
BC=7cm,点Q从点B开始沿BC边向点C以2cm/s的速度移动,
,
则,则,
∠B=90°,
中,
,
即,
整理得
解得(舍去)
3秒后,PQ的长度等于2cm;
(2)△PBQ的面积不能等于7cm2,理由如下,
设经过秒后,△PBQ的面积能否等于7cm2,
,
,
,
,
原方程无解,
即△PBQ的面积不能等于7cm2
【点睛】
本题考查了一元二次方程的应用,动点问题,一元二次方程根的判别式,根据题意列出方程是解题的关键.
23.端年节吃粽子是中国古老的传统习俗,某粽子批发店卖出每个粽子的利润为2元,根据员工情况,每天最多能做1100个,由市场调查得知,若每个粽子的单价降低x元,则粽子每天的销售量y(个)关于x(元)的函数关系式为y=800x+400.
(1)若每个粽子降价0.2元,则该店每天的销售量为 个,每天的总利润为 元.
(2)当每个粽子的单价降低多少元时,该店每天的总利润刚好是1200元?
【答案】(1)560个,1008元;(2)0.5元
【分析】
(1)把x=0.2代入已知函数关系式,求得相应的y值;然后由利润=每一个粽子的利润×数量求得总利润;
(2)根据利润=每一个粽子的利润×数量列出关于x的方程,通过解方程求得答案.
【详解】
解:(1)由题意可得:若每个粽子降价0.2元,则该店每天的销售量为800×0.2+400=560(个),
每天的总利润为:560×(2﹣0.2)=1008(元).
故答案是:560;1008;
(2)由题意,得(2﹣x)(800x+400)=1200,
解得:x=0.5或x=1.
当x=1时,y=800+400=1200>1100,超过每天可以制作的最大量,故不符合题意.
所以,当每个粽子的单价降低0.5元时,该店每天的总利润刚好是1200元.
【点睛】
本题主要考查了一元二次方程的应用,判断所求的解是否符合题意,舍去不合题意的解.找到关键描述语,找到等量关系准确的列出方程是解决问题的关键.
五、解答题(三)(每小题10分,共20分)
24.先阅读理解下面的例题,再按要求解答下列问题:
例题:求代数式的最小值.
解:
,
∵,
∴,
∴的最小值是4.
(1)代数式的最小值为___________;
(2)求代数式的最小值.
【答案】(1)5;(2)3
【分析】
(1)根据非负数的性质进行解答;
(2)把原式根据配方法化成:m2+2m+4=(m+1)2+3即可得出最小值.
【详解】
解:(1)∵,
∴,
∴的最小值是5,
故答案为:5;
(2),
∵,
∴,
∴的最小值是3.
【点睛】
本题考查了配方法的应用,难度不大,解题时要注意配方法的步骤.注意在变形的过程中不要改变式子的值.
25.在平面直角坐标系中,点O为坐标原点,直线AB与y轴、x轴分别相交于点A,点B,A点坐标为,B点坐标为,点C在直线AB上,过点C作轴,垂足为点D,连接OC,
(1)求直线AB的解析式.
(2)如图,点C在线段AB上,当时.
①求DC的长度.
②直接写出此时的面积.
(3)当面积是4时,直接写出此时点C的横坐标.
【答案】(1);(2)①;②(3)或
【分析】
(1)直接运用待定系数法求解即可;
(2)①,即为等腰直角三角形,点C在直线AB上,得出点C的横纵坐标相等,求解即可;
②直接运用三角形面积公式计算即可;
(3)设点C的坐标为:
【详解】
解:(1)设直线AB的解析式为:,
则,解得:,
∴一次函数的解析式为:;
(2)①设点C的坐标为:,
∵,
∴,
解得:,
∴;
②;
(3)设点C的坐标为:,
当点C在第一象限时:,
此方程无解,所以第一象限不存在点C;
当点C在第二象限时:,
解得:(舍),,
∴点C的横坐标为:;
当点C在第四象限时:,
解得:,(舍),
∴点C的横坐标为:,
综上:当面积是4时,直接写出此时点C的横坐标为:或.
【点睛】
本题考查了一次函数的综合问题,待定系数法求一次函数解析式,一次函数上点的坐标特征,根据题意设出点的坐标,列出方程是解本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第二章《一元二次方程》检测卷
第I卷(选择题)
一、选择题(每小题3分,共30分)
1.下列方程中一元二次方程的个数为( )
①;②;③;④.
A.1个 B.2个 C.3个 D.4个
2.用配方法解一元二次方程,下列变形正确的的是( )
A. B.
C. D.
3.已知关于x的一元二次方程有两个不相等的实数根,则m的取值范围是 ( )
A.m≥2 B.m<2 C.m≥0 D.m<0
4.如图,一农户要建一个矩形花圃,花圃的一边利用长为12m的住房墙,另外三边用25m长的篱笆围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门,花圃面积为80m2,设与墙垂直的一边长为xm(已标注在图中),则可以列出关于x的方程是( )
A.x(26﹣2x)=80 B.x(24﹣2x)=80
C.(x﹣1)(26﹣2x)=80 D.x(25﹣2x)=80
5.观察下列表格,可以作为一元二次方程的一个近似解的为( )
A. B. C. D.
6.已知:毕业典礼后,小芳学习小组内部的名同学,每两个同学都互相交换了礼物,她们一共买了份礼物.根据以上条件可以列出以下哪个方程( )
A. B.
C. D.
7.设a,b是方程的两个实数根,则的值为( )
A.2018 B.2020 C.2021 D.2024
8.定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.如图,在平面直角坐标系xOy中,矩形OABC的边OA=3,OC=4,点M(2,0),在边AB存在点P,使得△CMP为“智慧三角形”,则点P的坐标为( )
A.(3,1)或(3,3) B.(3,)或(3,3)
C.(3,)或(3,1) D.(3,)或(3,1)或(3,3)
9.若一元二次方程无实数根,则一次函数的图像经过第( )
A.二、三、四象限 B.一、三、四象限 C.一、二、四象限 D.一、二、三象限
10.对于一元二次方程,下列说法:
①若,则;
②若方程有两个不相等的实根,则方程必有两个不相等的实根;
③若是方程的一个根,则一定有成立;
④若是一元二次方程的根,则.
其中正确的有( )
A.个 B.个 C.个 D.个
第II卷(非选择题)
二、填空题(每小题4分,共28分)
11.方程的解是______.
12.已知、是一元二次方程的两个实数根,则的值是_____.
13.已知两直角边的长度恰好是一元二次方程的两个实数根,那么的面积是______.
14.关于x的方程是,那么当m___________时,方程为一元二次方程.
15.一元二次方程有一根为,则另一个根为__________.
16.若,则的值为__________.
17.有一张长40cm,宽30cm的长方形硬纸片(如图1),截去四个全等的小正方形之后,折成无盖的纸盒(如图2).若纸盒的底面积为600cm2,则纸盒的高为__________.
三、解答题(一)(每小题6分,共18分)
18.解一元二次方程:
(1)
(2)
19.求证:不论k取何实数,方程都没有实根.
20.某地区2019年投入教育经费2000万元,2021年投入教育经费2880万元.
(1)求2019年至2021年该地区投入教育经费的年平均增长率;
(2)根据(1)所得的年平均增长率,预计2022年该地区将投入教育经费多少万元.
四、解答题(二)(每小题8分,共24分)
21.已知关于x的一元二次方程有两个不相等的实数根.
(1)求实数k的取值范围;
(2)设方程两个实数根分别为,,且满足,求k的值.
22.如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.若P,Q两点同时出发,当点Q运动到点C时,P,Q两点同时停止运动.求:
(1)几秒后,PQ的长度等于2cm?
(2)△PBQ的面积能否等于7cm2?说明理由.
23.端年节吃粽子是中国古老的传统习俗,某粽子批发店卖出每个粽子的利润为2元,根据员工情况,每天最多能做1100个,由市场调查得知,若每个粽子的单价降低x元,则粽子每天的销售量y(个)关于x(元)的函数关系式为y=800x+400.
(1)若每个粽子降价0.2元,则该店每天的销售量为 个,每天的总利润为 元.
(2)当每个粽子的单价降低多少元时,该店每天的总利润刚好是1200元?
五、解答题(三)(每小题10分,共20分)
24.先阅读理解下面的例题,再按要求解答下列问题:
例题:求代数式的最小值.
解:
,
∵,
∴,
∴的最小值是4.
(1)代数式的最小值为___________;
(2)求代数式的最小值.
25.在平面直角坐标系中,点O为坐标原点,直线AB与y轴、x轴分别相交于点A,点B,A点坐标为,B点坐标为,点C在直线AB上,过点C作轴,垂足为点D,连接OC,
(1)求直线AB的解析式.
(2)如图,点C在线段AB上,当时.
①求DC的长度.
②直接写出此时的面积.
(3)当面积是4时,直接写出此时点C的横坐标.
第二章《一元二次方程》检测卷
第I卷(选择题)
一、选择题(每小题3分,共30分)
1.下列方程中一元二次方程的个数为( )
①;②;③;④.
A.1个 B.2个 C.3个 D.4个
【答案】A
【分析】
根据一元二次方程的定义直接判断即可.
【详解】
解:是一元二次方程;
含有两个未知数,不是一元二次方程;
未知数在根号内,不是一元二次方程;
未知数在分母中,不是一元二次方程;
故选:A.
【点睛】
本题考查了一元二次方程的定义,明确只含有一个未知数,未知数的最高次为2次的整式方程是一元二次方程是解题关键.
2.用配方法解一元二次方程,下列变形正确的的是( )
A. B.
C. D.
【答案】D
【分析】
根据完全平方式的特点,先移项,再两边加一次项系数一半的平方.
【详解】
解:,
∴,
∴.
故选:D.
【点睛】
本题考查了解一元二次方程-配方法:将一元二次方程配成(x+m)2=n的形式,再利用直接开平方法求解,这种解一元二次方程的方法叫配方法.
3.已知关于x的一元二次方程有两个不相等的实数根,则m的取值范围是 ( )
A.m≥2 B.m<2 C.m≥0 D.m<0
【答案】B
【分析】
根据根的判别式,可知Δ>0,据此即可求出m的取值范围.
【详解】
解:∵关于x的一元二次方程有两个不相等的实数根,
∴
Δ=,
解得:m<2,
故选:B
【点睛】
此题考查了根的判别式,解题时要注意一元二次方程成立的条件:二次项系数不为0
4.如图,一农户要建一个矩形花圃,花圃的一边利用长为12m的住房墙,另外三边用25m长的篱笆围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门,花圃面积为80m2,设与墙垂直的一边长为xm(已标注在图中),则可以列出关于x的方程是( )
A.x(26﹣2x)=80 B.x(24﹣2x)=80
C.(x﹣1)(26﹣2x)=80 D.x(25﹣2x)=80
【答案】A
【分析】
设与墙垂直的一边长为xm,则与墙平行的一边长为(26﹣2x)m,根据花圃面积为80m2即可列出关于x的一元二次方程,此题得解.
【详解】
解:设与墙垂直的一边长为xm,则与墙平行的一边长为(26﹣2x)m,
根据题意得:x(26﹣2x)=80.
故选:A.
【点睛】
本题主要考查了一元二次方程的应用,明确题意,准确找到等量关系是解题的关键.
5.观察下列表格,可以作为一元二次方程的一个近似解的为( )
A. B. C. D.
【答案】B
【分析】
根据表格中的数据,可判断代数式的值为4.61和4.56时,对应的值为-1.12和-1.11,观察原方程可理解为求代数式的值为4.6时,对应的的值范围,由此判断即可.
【详解】
解:∵时,;时,;
∴时,对应应满足,
∵-1.123<-1.12<-1.117<-1.11<-1.089<-1.073
∴原方程的近似解为:-1.117,
故选:B.
【点睛】
本题考查一元二次方程的近似解,理解表格中的数据,掌握求近似解的方法先求x的范围,再比较大小选取是解题关键.
6.已知:毕业典礼后,小芳学习小组内部的名同学,每两个同学都互相交换了礼物,她们一共买了份礼物.根据以上条件可以列出以下哪个方程( )
A. B.
C. D.
【答案】C
【分析】
根据每两名同学之间交换礼物一个,则m人共赠贺卡m(m-1)张,列方程即可.
【详解】
解:根据题意,得
m(m-1)=20,
故选C.
【点睛】
此题主要考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.
7.设a,b是方程的两个实数根,则的值为( )
A.2018 B.2020 C.2021 D.2024
【答案】A
【分析】
根据根与系数的关系和一元二次方程的解得出,,将变形后代入,即可求出答案.
【详解】
解:∵a,b是方程的两个实数根,
∴,
∴.
故选:A.
【点睛】
本题考查了根与系数的关系和一元二次方程的解,能求出和是解此题的关键.
8.定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.如图,在平面直角坐标系xOy中,矩形OABC的边OA=3,OC=4,点M(2,0),在边AB存在点P,使得△CMP为“智慧三角形”,则点P的坐标为( )
A.(3,1)或(3,3) B.(3,)或(3,3)
C.(3,)或(3,1) D.(3,)或(3,1)或(3,3)
【答案】D
【分析】
由题意可知,“智慧三角形”是直角三角形,∠CPM=90°或∠CMP=90°,设P(3,a),则AP=a,BP=4 a;分两种情况:①若∠CPM=90°,②若∠CMP=90°,根据勾股定理分别求出CP2、MP2、CM2,并根据图形列出关于a的方程,解得a的值,则可得答案.
【详解】
解:由题意可知,“智慧三角形”是直角三角形,∠CPM=90°或∠CMP=90°,
∴设P(3,a),则AP=a,BP=4 a;
①若∠CPM=90°,在Rt△BCP中,由勾股定理得:
CP2=BP2+BC2=(4 a)2+9,
在Rt△MPA中,由勾股定理得:
MP2=MA2+AP2=1+a2,
在Rt△MPC中,由勾股定理得:
CM2=MP2+CP2=1+a2+(4 a)2+9=2a2 8a+26,
又∵CM2=OM2+OC2=4+16=20,
∴2a2 8a+26=20,
∴(a 3)(a 1)=0,
解得:a=3或a=1,
∴P(3,3)或(3,1);
②若∠CMP=90°,在Rt△BCP中,由勾股定理得:
CP2=BP2+BC2=(4 a)2+9,
在Rt△MPA中,由勾股定理得:
MP2=MA2+AP2=1+a2,
∵CM2=OM2+OC2=20,
在Rt△MCP中,由勾股定理得:
CM2+MP2=CP2,
∴20+1+a2=(4 a)2+9,
解得:a=.
∴P(3,).
综上,P(3,)或(3,1)或(3,3).
故选:D.
【点睛】
本题考查了矩形的性质及勾股定理在几何图形坐标计算中的应用,数形结合、分类讨论并根据题意正确地列式是解题的关键.
9.若一元二次方程无实数根,则一次函数的图像经过第( )
A.二、三、四象限 B.一、三、四象限 C.一、二、四象限 D.一、二、三象限
【答案】A
【分析】
先根据一元二次方程无实数根,利用判别式求出m的取值范围,然后判断一次函数经过的象限即可.
【详解】
解:由已知得:,
解得,
∵一次函数中,,
∴该一次函数图像在第二、三、四象限,
故选A.
【点睛】
本题主要考查了一元二次方程根的判别式,根据函数解析式判断函数经过的象限,解题的关键在于能够熟练掌握一元二次方程根的判别式.
10.对于一元二次方程,下列说法:
①若,则;
②若方程有两个不相等的实根,则方程必有两个不相等的实根;
③若是方程的一个根,则一定有成立;
④若是一元二次方程的根,则.
其中正确的有( )
A.个 B.个 C.个 D.个
【答案】C
【分析】
按照方程的解的含义、一元二次方程的实数根与判别式的关系、等式的性质、一元二次方程的求根公式等对各选项分别讨论,可得答案.
【详解】
解:①若a+b+c=0,则x=1是方程ax2+bx+c=0的解,
由一元二次方程的实数根与判别式的关系可知:Δ=b2-4ac≥0,故①正确;
②方程ax2+c=0有两个不相等的实根,
∴Δ=0-4ac>0,
∴-4ac>0
则方程ax2+bx+c=0的判别式Δ=b2-4ac>0,
∴方程ax2+bx+c=0必有两个不相等的实根,故②正确;
③∵c是方程ax2+bx+c=0的一个根,
则ac2+bc+c=0,
∴c(ac+b+1)=0,
若c=0,等式仍然成立,
但ac+b+1=0不一定成立,故③不正确;
④若x0是一元二次方程ax2+bx+c=0的根,
则由求根公式可得:x0=,
∴2ax0+b=±,
∴b2-4ac=(2ax0+b)2,故④正确.
故正确的有①②④,
故选:C.
【点睛】
本题考查一元二次方程根的判断,根据方程形式,判断根的情况是求解本题的关键.
第II卷(非选择题)
二、填空题(每小题4分,共28分)
11.方程的解是______.
【答案】,
【分析】
先移项,使方程右边为0,再提公因式,然后根据“两式相乘值为0,这两式中至少有一式值为0”进行求解.
【详解】
解:原方程可化为:,
因式分解得:,
所以或,
解得:,,
故答案为:,.
【点睛】
本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.本题运用的是因式分解法.
12.已知、是一元二次方程的两个实数根,则的值是_____.
【答案】
【分析】
根据一元二次方程的根与系数的关系计算.
【详解】
解:由题意可得:,
∴=,
故答案为:.
【点睛】
此题考查一元二次方程的根与系数的关系,熟记根与系数的关系是解题的关键.
13.已知两直角边的长度恰好是一元二次方程的两个实数根,那么的面积是______.
【答案】6
【分析】
设两直角边的长度分别为,n,则,n是方程的两个实数根,再利用一元二次方程的根与系数的关系即可求得答案.
【详解】
解:设两直角边的长度分别为,n,
由题意可得:,n是方程的两个实数根,
∴,
∴,
故答案为:6.
【点睛】
本题考查了一元二次方程的根与系数的关系,若,是一元二次方程的两根时,则,,熟练掌握根与系数的关系是解决本题的关键.
14.关于x的方程是,那么当m___________时,方程为一元二次方程.
【答案】≠±1
【分析】
由一元二次方程的二次项系数不能是0,可以确定m的取值
【详解】
解:若方程是一元二次方程,则:m2 1≠0,
∴m≠±1,
故答案是:≠±1.
【点睛】
本题考查的是一元二次方程的定义:含有一个未知数,并且未知数的最高次数是2的整式方程是一元二次方程,掌握一元二次方程的定义是解题的关键.
15.一元二次方程有一根为,则另一个根为__________.
【答案】
【分析】
根据一元二次方程的根与系数的关系来求方程的另一个根.
【详解】
解:设是关于x的一元二次方程的两个根.
由韦达定理,得,即,
解得,,
即方程的另一个根为1.
故答案为:1.
【点睛】
本题考查了根与系数的关系,在利用根与系数的关系时,要注意等式中的a、b、c所表示的含义.
16.若,则的值为__________.
【答案】-4或2
【分析】
先用换元法把方程转化为一元二次方程,再利用十字相乘法因式分解的形式,即可求解.
【详解】
解:2x+3y=t,原方程可变形为:t2+2t-8=0,
∴(t+4)(t-2)=0,
解得,t=-4或2;
∴2x+3y的值为-4或2.
故答案为:-4或2.
【点睛】
本题考查了一元二次方程的解法和换元法的运用,解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.
17.有一张长40cm,宽30cm的长方形硬纸片(如图1),截去四个全等的小正方形之后,折成无盖的纸盒(如图2).若纸盒的底面积为600cm2,则纸盒的高为__________.
【答案】5cm
【分析】
设纸盒的高是,根据题意,其底面的长宽分别为(40-2x)cm和(30-2x)cm,根据长方形面积公式列方程求解即可.
【详解】
解:设纸盒的高是.
依题意,得.
整理得.
解得,(不合题意,舍去).
答:纸盒的高为.
【点睛】
本题考查一元二次方程的应用,根据题意用含x的式子表示底面的长和宽,正确列方程,解方程是本题的解题关键.
三、解答题(一)(每小题6分,共18分)
18.解一元二次方程:
(1)
(2)
【答案】(1),;(2),
【分析】
(1)根据一元二次方程的求根公式即可求解;
(2)利用因式分解法求解一元二次方程即可.
【详解】
(1).
解:,,,
,
.
,.
(2)解:
或
,.
【点睛】
此题主要考查一元二次方程的求解,解题的关键是熟知公式法及因式分解法的运用.
19.求证:不论k取何实数,方程都没有实根.
【答案】见解析
【分析】
先根据得到即可得到方程是一元二次方程,然后利用一元二次方程根的判别式进行求解即可.
【详解】
解:∵,
∴,
∴方程是一元二次方程,
∴
,
∵,
∴,
∴,即恒成立,
∴方程都没有实根.
【点睛】
本题主要考查了一元二次方程根的判别式,完全平方公式,解题的关键在于能够熟练掌握相关知识进行求解.
20.某地区2019年投入教育经费2000万元,2021年投入教育经费2880万元.
(1)求2019年至2021年该地区投入教育经费的年平均增长率;
(2)根据(1)所得的年平均增长率,预计2022年该地区将投入教育经费多少万元.
【答案】(1)2019年至2021年该地区投入教育经费的年平均增长率为20%,(2) 2022年该地区将投入教育经费3456万元.
【分析】
(1)设年平均增长率为x,一般用增长后的量=增长前的量×(1+增长率),2019年投入教育经费是2000万元,2020年在2019年的基础上增长x,就是2019年的教育经费数额的倍,2021年在2020年的基础上再增长x,2020年的教育经费数额为2000,即可列出方程求解;
(2)利用(1)中求得的增长率来求2022年该地区将投入教育经费.
【详解】
解:(1)设年平均增长率为x,由题意得:
2000×(1+x)2=2880,
解得:x1=0.2, x2=-2.2(舍去),
答2019年至2021年该地区投入教育经费的年平均增长率为20%;
(2) 2880×(1+20%)=3456(万元),
答:2022年该地区将投入教育经费3456万元.
【点睛】
本题考查了一元二次方程中增长率的知识.掌握增长前的量×(1+年平均增长率) =增长后的量是本题的关键.
四、解答题(二)(每小题8分,共24分)
21.已知关于x的一元二次方程有两个不相等的实数根.
(1)求实数k的取值范围;
(2)设方程两个实数根分别为,,且满足,求k的值.
【答案】(1)且;(2).
【分析】
(1)根据一元二次方程根的判别式和一元二次方程的定义求解即可;
(2)根据一元二次方程根与系数的关系求解即可.
【详解】
解:(1)∵方程有两个不相等的实数根,
∴且,即且,
解得且;
(2)由根与系数的关系可得,,
由题意可得,即,
∴
解得或,
经检验可知:,都是原分式方程的解.
由(1)可知且
∴.
【点睛】
本题主要考查了解分式方程,解一元二次方程,一元二次方程的定义,一元二次方程根与系数的关系,解题的关键在于能够熟练掌握相关知识进行求解.
22.如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.若P,Q两点同时出发,当点Q运动到点C时,P,Q两点同时停止运动.求:
(1)几秒后,PQ的长度等于2cm?
(2)△PBQ的面积能否等于7cm2?说明理由.
【答案】(1)3;(2)不能,理由见解析
【分析】
(1)根据题意,设运动时间为秒,进而分别写出的长,进而根据勾股定理列出方程即可;
(2)根据题意列出方程,根据根的判别式进行判断即可
【详解】
(1)设经过秒后,PQ的长度等于2cm,依题意得,
BC=7cm,点Q从点B开始沿BC边向点C以2cm/s的速度移动,
,
则,则,
∠B=90°,
中,
,
即,
整理得
解得(舍去)
3秒后,PQ的长度等于2cm;
(2)△PBQ的面积不能等于7cm2,理由如下,
设经过秒后,△PBQ的面积能否等于7cm2,
,
,
,
,
原方程无解,
即△PBQ的面积不能等于7cm2
【点睛】
本题考查了一元二次方程的应用,动点问题,一元二次方程根的判别式,根据题意列出方程是解题的关键.
23.端年节吃粽子是中国古老的传统习俗,某粽子批发店卖出每个粽子的利润为2元,根据员工情况,每天最多能做1100个,由市场调查得知,若每个粽子的单价降低x元,则粽子每天的销售量y(个)关于x(元)的函数关系式为y=800x+400.
(1)若每个粽子降价0.2元,则该店每天的销售量为 个,每天的总利润为 元.
(2)当每个粽子的单价降低多少元时,该店每天的总利润刚好是1200元?
【答案】(1)560个,1008元;(2)0.5元
【分析】
(1)把x=0.2代入已知函数关系式,求得相应的y值;然后由利润=每一个粽子的利润×数量求得总利润;
(2)根据利润=每一个粽子的利润×数量列出关于x的方程,通过解方程求得答案.
【详解】
解:(1)由题意可得:若每个粽子降价0.2元,则该店每天的销售量为800×0.2+400=560(个),
每天的总利润为:560×(2﹣0.2)=1008(元).
故答案是:560;1008;
(2)由题意,得(2﹣x)(800x+400)=1200,
解得:x=0.5或x=1.
当x=1时,y=800+400=1200>1100,超过每天可以制作的最大量,故不符合题意.
所以,当每个粽子的单价降低0.5元时,该店每天的总利润刚好是1200元.
【点睛】
本题主要考查了一元二次方程的应用,判断所求的解是否符合题意,舍去不合题意的解.找到关键描述语,找到等量关系准确的列出方程是解决问题的关键.
五、解答题(三)(每小题10分,共20分)
24.先阅读理解下面的例题,再按要求解答下列问题:
例题:求代数式的最小值.
解:
,
∵,
∴,
∴的最小值是4.
(1)代数式的最小值为___________;
(2)求代数式的最小值.
【答案】(1)5;(2)3
【分析】
(1)根据非负数的性质进行解答;
(2)把原式根据配方法化成:m2+2m+4=(m+1)2+3即可得出最小值.
【详解】
解:(1)∵,
∴,
∴的最小值是5,
故答案为:5;
(2),
∵,
∴,
∴的最小值是3.
【点睛】
本题考查了配方法的应用,难度不大,解题时要注意配方法的步骤.注意在变形的过程中不要改变式子的值.
25.在平面直角坐标系中,点O为坐标原点,直线AB与y轴、x轴分别相交于点A,点B,A点坐标为,B点坐标为,点C在直线AB上,过点C作轴,垂足为点D,连接OC,
(1)求直线AB的解析式.
(2)如图,点C在线段AB上,当时.
①求DC的长度.
②直接写出此时的面积.
(3)当面积是4时,直接写出此时点C的横坐标.
【答案】(1);(2)①;②(3)或
【分析】
(1)直接运用待定系数法求解即可;
(2)①,即为等腰直角三角形,点C在直线AB上,得出点C的横纵坐标相等,求解即可;
②直接运用三角形面积公式计算即可;
(3)设点C的坐标为:
【详解】
解:(1)设直线AB的解析式为:,
则,解得:,
∴一次函数的解析式为:;
(2)①设点C的坐标为:,
∵,
∴,
解得:,
∴;
②;
(3)设点C的坐标为:,
当点C在第一象限时:,
此方程无解,所以第一象限不存在点C;
当点C在第二象限时:,
解得:(舍),,
∴点C的横坐标为:;
当点C在第四象限时:,
解得:,(舍),
∴点C的横坐标为:,
综上:当面积是4时,直接写出此时点C的横坐标为:或.
【点睛】
本题考查了一次函数的综合问题,待定系数法求一次函数解析式,一次函数上点的坐标特征,根据题意设出点的坐标,列出方程是解本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
