数学九年级北师大版何时获得最大利润
图片预览




文档简介
(共14张PPT)
2.6 何时获得最大利润
前段时间以2.5元进的T恤衫销售怎么样?
还不错,若以单价13.5元销售,十天可以销售500件,若单价每降低一元,就可多售出200件。
那你得赶快制订一个销售方案,单价到底定为多少时这批货所获利润最多?
到底单价多少,利润最多呢?
?
设销售价为x元(x≤13.5元),那么
某商店经营T恤衫,已知成批购进时单价是2.5元.根据市场调查,销售量与单价满足如下关系:在一时间内,单价是13.5元时,销售量是500件,而单价每降低1元,就可以多售出200件.
驶向胜利的彼岸
销售量可表示为 : 件;
销售额可表示为: 元;
所获利润可表示为: 元;
当销售单价为 元时,可以获得最大利润,最大利润是 元.
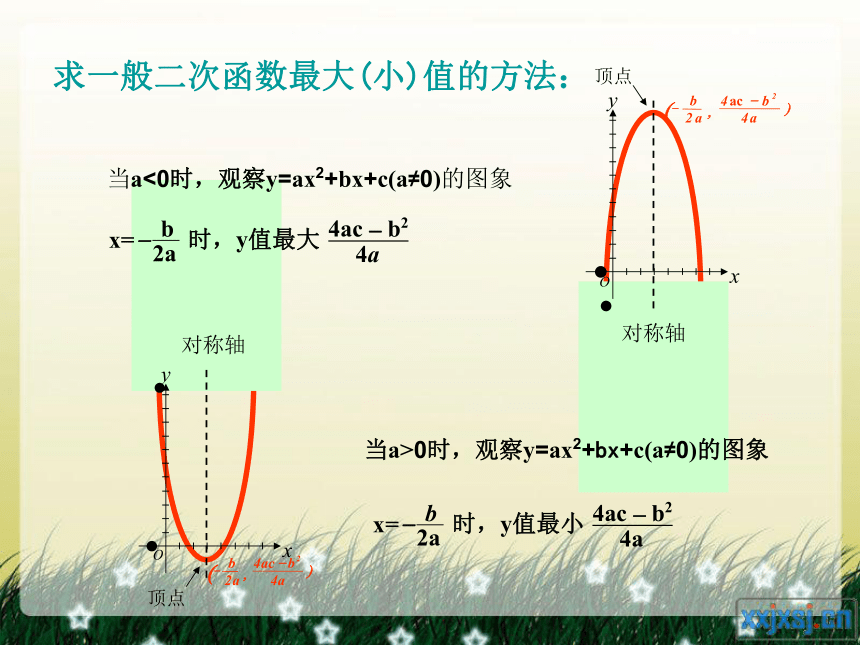
当a<0时,观察y=ax2+bx+c(a≠0)的图象
顶点
对称轴
顶点
y
x
O
y
x
O
时,y值最大
4ac - b2
4a
2a
b
x=
-
2
a
b
-
(
a
b
ac
4
4
2
-
,
)
2
a
b
-
(
a
b
ac
4
4
2
-
,
)
对称轴
当a>0时,观察y=ax2+bx+c(a≠0)的图象
时,y值最小
4ac - b2
4a
2a
b
x=
-
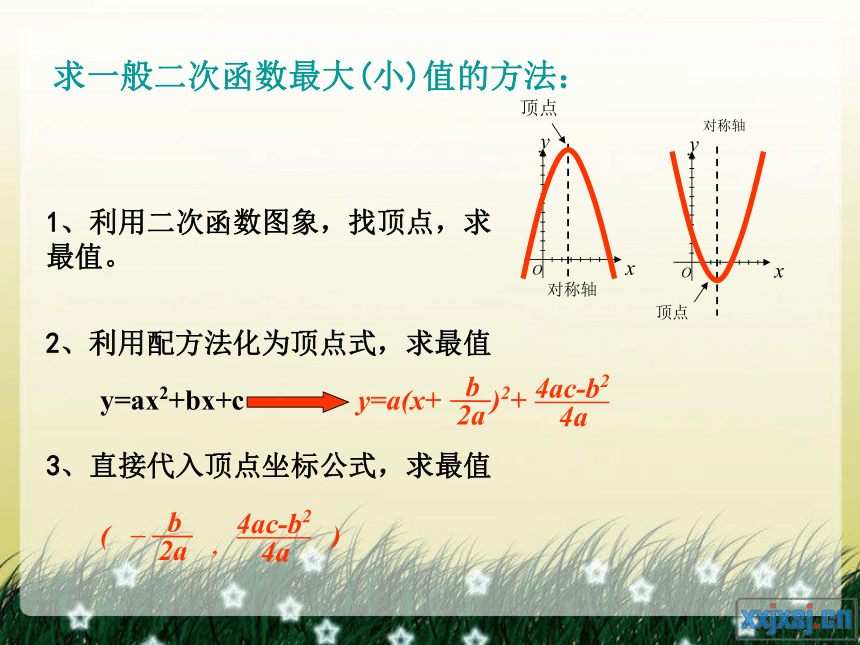
求一般二次函数最大(小)值的方法:
求一般二次函数最大(小)值的方法:
1、利用二次函数图象,找顶点,求 最值。
2、利用配方法化为顶点式,求最值
3、直接代入顶点坐标公式,求最值
对称轴
顶点
y
x
O
顶点
y
x
O
对称轴
y=ax2+bx+c
y=a(x+ )2+
b
2a
4ac-b2
4a
( )
b
2a
4ac-b2
4a
-
,
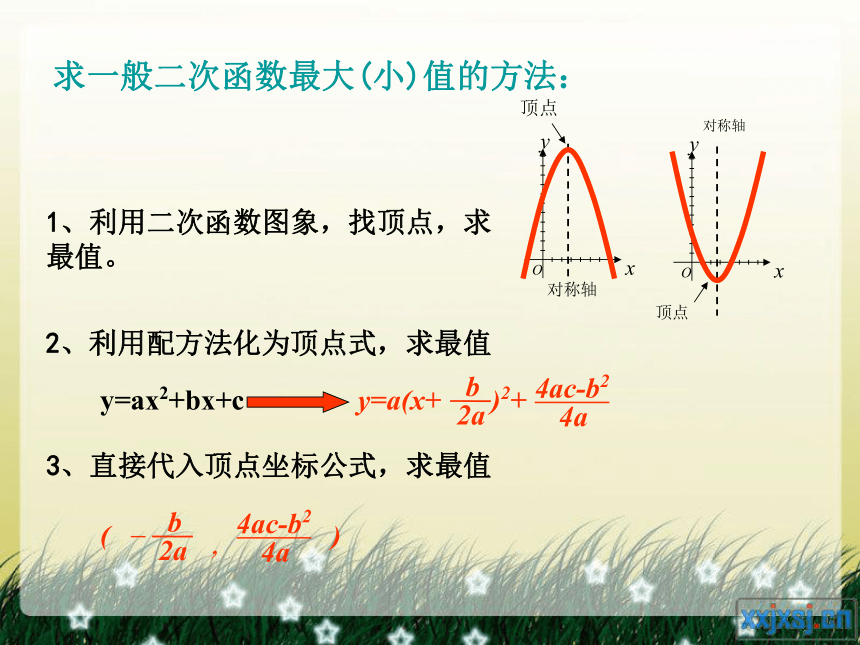
求一般二次函数最大(小)值的方法:
1、利用二次函数图象,找顶点,求 最值。
2、利用配方法化为顶点式,求最值
3、直接代入顶点坐标公式,求最值
对称轴
顶点
y
x
O
顶点
y
x
O
对称轴
y=ax2+bx+c
y=a(x+ )2+
b
2a
4ac-b2
4a
( )
b
2a
4ac-b2
4a
-
,
何时橙子总产量最大
还记得本章一开始涉及的“种多少棵橙子树”的问题吗?
第二章 二次函数
九年级 数学
1、 在本章第一节“种多少棵橙子树”的问题中,我们得到表示增种橙子树的数量x(棵)与橙子总产量y(个)的二次函数表达式:
60000
100
5
2
+
+
-
=
x
x
y
我们也曾利用列表的方法得到一个猜想:当x=10时,橙子的总产量最多,现在请你验证一下你的猜想是否正确。你是怎样做的?与同伴交流。
可以利用配方化为顶点式、顶点坐标公式图象法求该二次函数的最大值。
做一做
当x=10时,y=60500.
O
5
10
15
20
60000
6020060100
60300
60400
60500
60600
x/棵
y/个
2、(1)利用函数图象描述橙子的总产量
与增种橙子树的棵数之间的关系。
(2)增种多少棵橙子树,可以使橙子
的总产量在60400个以上?
答案:(1)当x<10时,橙子的总产量随增种橙子树的增加而增加;
当x>10时,橙子的总产量随增种橙子树的增加而减少。
(2)6、7、8、9、10、11、12、13、14棵
议一议
日用品何时获得最大利润
3.某商店购进一批单价为20元的日用品,如果以单价30元销售,那么半个月内可以售出400件.根据销售经验,提高单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件.如何提高售价,才能在半个月内获得最大利润
随堂练习P60
4
驶向胜利的彼岸
设销售价为x元(x≥30元), 利润为y元,则
活学活用
观察图象,下列的二次函数有最大值、最小值吗?如果有,分别是多少?
0
1
2
3
-1
-3
-2
-4
-8
-6
-10
-11
X
y
y=x2+2x-10(-3 x 2.5)
0
1
2
3
4
5
6
7
1
2
3
4
5
6
7
8
y=4x-0.5x2(0 x 7 )
X
y
2、利用二次函数知识解决实际问题中最值的步骤:
1、求二次函数最值的方法:
(1)利用图象,找顶点,求最值;
(2)利用配方化为顶点式,求最值;
(3)利用顶点坐标公式,求最值。
实际问题
提出最值问题
建立二次函数关系式
求出最值
实际问题
结论
判断是否
符合实际背景
符合
检验
转化
分析
计算
解决
谈谈你的收获和体会!
解决实际问题时一定要注意二次函数自变量的取值范围。
教材65页
随堂练习 1题
习题2.7 1题、2题。
课后作业
结束寄语
生活是数学的源泉。
下课了!
2.6 何时获得最大利润
前段时间以2.5元进的T恤衫销售怎么样?
还不错,若以单价13.5元销售,十天可以销售500件,若单价每降低一元,就可多售出200件。
那你得赶快制订一个销售方案,单价到底定为多少时这批货所获利润最多?
到底单价多少,利润最多呢?
?
设销售价为x元(x≤13.5元),那么
某商店经营T恤衫,已知成批购进时单价是2.5元.根据市场调查,销售量与单价满足如下关系:在一时间内,单价是13.5元时,销售量是500件,而单价每降低1元,就可以多售出200件.
驶向胜利的彼岸
销售量可表示为 : 件;
销售额可表示为: 元;
所获利润可表示为: 元;
当销售单价为 元时,可以获得最大利润,最大利润是 元.
当a<0时,观察y=ax2+bx+c(a≠0)的图象
顶点
对称轴
顶点
y
x
O
y
x
O
时,y值最大
4ac - b2
4a
2a
b
x=
-
2
a
b
-
(
a
b
ac
4
4
2
-
,
)
2
a
b
-
(
a
b
ac
4
4
2
-
,
)
对称轴
当a>0时,观察y=ax2+bx+c(a≠0)的图象
时,y值最小
4ac - b2
4a
2a
b
x=
-
求一般二次函数最大(小)值的方法:
求一般二次函数最大(小)值的方法:
1、利用二次函数图象,找顶点,求 最值。
2、利用配方法化为顶点式,求最值
3、直接代入顶点坐标公式,求最值
对称轴
顶点
y
x
O
顶点
y
x
O
对称轴
y=ax2+bx+c
y=a(x+ )2+
b
2a
4ac-b2
4a
( )
b
2a
4ac-b2
4a
-
,
求一般二次函数最大(小)值的方法:
1、利用二次函数图象,找顶点,求 最值。
2、利用配方法化为顶点式,求最值
3、直接代入顶点坐标公式,求最值
对称轴
顶点
y
x
O
顶点
y
x
O
对称轴
y=ax2+bx+c
y=a(x+ )2+
b
2a
4ac-b2
4a
( )
b
2a
4ac-b2
4a
-
,
何时橙子总产量最大
还记得本章一开始涉及的“种多少棵橙子树”的问题吗?
第二章 二次函数
九年级 数学
1、 在本章第一节“种多少棵橙子树”的问题中,我们得到表示增种橙子树的数量x(棵)与橙子总产量y(个)的二次函数表达式:
60000
100
5
2
+
+
-
=
x
x
y
我们也曾利用列表的方法得到一个猜想:当x=10时,橙子的总产量最多,现在请你验证一下你的猜想是否正确。你是怎样做的?与同伴交流。
可以利用配方化为顶点式、顶点坐标公式图象法求该二次函数的最大值。
做一做
当x=10时,y=60500.
O
5
10
15
20
60000
6020060100
60300
60400
60500
60600
x/棵
y/个
2、(1)利用函数图象描述橙子的总产量
与增种橙子树的棵数之间的关系。
(2)增种多少棵橙子树,可以使橙子
的总产量在60400个以上?
答案:(1)当x<10时,橙子的总产量随增种橙子树的增加而增加;
当x>10时,橙子的总产量随增种橙子树的增加而减少。
(2)6、7、8、9、10、11、12、13、14棵
议一议
日用品何时获得最大利润
3.某商店购进一批单价为20元的日用品,如果以单价30元销售,那么半个月内可以售出400件.根据销售经验,提高单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件.如何提高售价,才能在半个月内获得最大利润
随堂练习P60
4
驶向胜利的彼岸
设销售价为x元(x≥30元), 利润为y元,则
活学活用
观察图象,下列的二次函数有最大值、最小值吗?如果有,分别是多少?
0
1
2
3
-1
-3
-2
-4
-8
-6
-10
-11
X
y
y=x2+2x-10(-3 x 2.5)
0
1
2
3
4
5
6
7
1
2
3
4
5
6
7
8
y=4x-0.5x2(0 x 7 )
X
y
2、利用二次函数知识解决实际问题中最值的步骤:
1、求二次函数最值的方法:
(1)利用图象,找顶点,求最值;
(2)利用配方化为顶点式,求最值;
(3)利用顶点坐标公式,求最值。
实际问题
提出最值问题
建立二次函数关系式
求出最值
实际问题
结论
判断是否
符合实际背景
符合
检验
转化
分析
计算
解决
谈谈你的收获和体会!
解决实际问题时一定要注意二次函数自变量的取值范围。
教材65页
随堂练习 1题
习题2.7 1题、2题。
课后作业
结束寄语
生活是数学的源泉。
下课了!
