13.3.1等腰三角形 同步练习2020-2021学年人教版数学八年级上册(Word版含答案)
文档属性
| 名称 | 13.3.1等腰三角形 同步练习2020-2021学年人教版数学八年级上册(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 557.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-15 11:53:17 | ||
图片预览




文档简介
等腰三角形
一、单选题
1.已知等腰三角形两边的长分别为3和7,则此等腰三角形的周长为( )
A.13 B.17 C.13或17 D.13或10
2.已知在△ABC中,AB=AC,且∠B=α,则α的取值范围是( )
A.a≤45° B.0° < α < 90° C.α=90° D.90° < α < 180°
3.如图,点是内一点,,,则以下结论:①②③平分④与的位置关系是互相垂直.其中正确的有( )个
A.0 B.1 C.2 D.3
4.在等腰三角形中,AB的长是BC的2倍,周长为40,则AB的长为( )
A.20 B.16 C.16或20 D.以上都不对
5.已知:如图,经过线段一端点A有一直线l,直线上l存在点C,使为等腰三角形,这样的点C有( )个.
A.2 B.3 C.4 D.5
6.如图,在等腰△ABC中,AB=AC,点D、E、F分别是边AB、BC、CA上的点,DE与BF相交于点G,BD=BC,BE=CF,若∠A=40°,则∠DGF的度数为( )
A.40° B.60° C.70° D.110°
7.如图,在中,,,则( )
A. B.
C. D.
8.如图,在中,,,观察图中尺规作图的痕迹,可知的度数为( )
A.40° B.50° C.55° D.60°
9.如图,等腰底边的长为,面积是,为边上的中点,腰的垂直平分线交于,交于点,则的值为( )
A. B. C. D.
10.如图,为了让电线杆垂直于地面,工程人员的操作方法是:从电线杆DE上一点A往地面拉两条长度相等的固定绳AB与AC,当固定点B,C到杆脚E的距离相等,且B,EC在同一直线上时,电线杆DE就垂直于BC工程人员这种操作方法的依据是( )
A.等边对等角 B.等角对等边
C.垂线段最短 D.等腰三角形“三线合一”
11.如图,D是AB边上的中点,将ABC沿过D点的直线折叠,使点A落在BC上F处,若∠B=50°,则∠BDF的大小为( )
A.50° B.80° C.90° D.100°
12.如图,点B、C、E、在同一直线上,△ABC与△CDE为等腰三角形,CA=CB,CD=CE,∠ACB=∠DCE,∠BGC=∠AFC,则下列结论:①DG=EF;②CG=CF;③AE=BD;④AC+CD=AE.正确的有( )
A.3个 B.2个 C.1个 D.0个
二、填空题
13.如图,△ABC的面积为4cm2,BP平分∠ABC,且AP⊥BP于点P,则△PBC的面积为______cm2
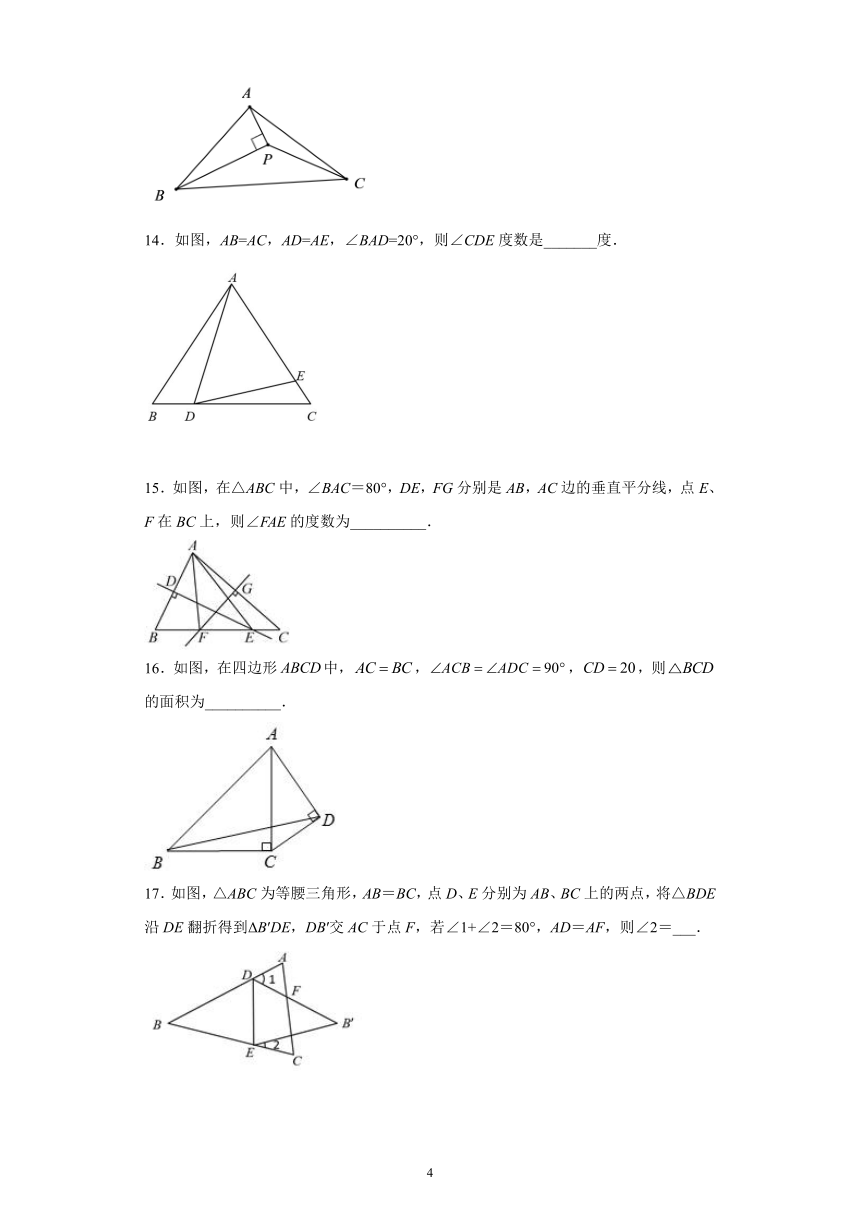
14.如图,AB=AC,AD=AE,∠BAD=20°,则∠CDE度数是_______度.
15.如图,在△ABC中,∠BAC=80°,DE,FG分别是AB,AC边的垂直平分线,点E、F在BC上,则∠FAE的度数为__________.
16.如图,在四边形中,,,,则的面积为__________.
17.如图,△ABC为等腰三角形,AB=BC,点D、E分别为AB、BC上的两点,将△BDE沿DE翻折得到ΔB′DE,DB′交AC于点F,若∠1+∠2=80°,AD=AF,则∠2=___.
三、解答题
18.如图,中,是的角平分线,,求证:.
19.如图,已知点、在△ABC的边上,,.
(1)求证:;
(2)若,求的度数.
20.如图,在中,的垂直平分线交于点,交于点,且,的周长等于26cm.
(1)求的长.
(2)若,且,求证:.
21.如图,已知四边形,连接,其中,,,延长到点,得,点为上一点,连接、,交于点.
(1)求证:;
(2)若,,试探究、的数量关系,并说明理由;
(3)如图2,连接,若,求的度数.
参考答案
1.B
解:①当腰是3,底边是7时,3+3<7不满足三角形的三边关系,因此舍去.
②当底边是3,腰长是7时,7+7>3能构成三角形,则其周长=3+7+7=17.
故选:B.
2.B
解:∵在△ABC中,AB=AC,∠B=α,
∴∠B=∠C=α,
∵三角形内角和∠A+∠B+∠C=180°,
∴∠B+∠C<180°,
即:2α<180°,
∴α<90°,
又由题意可知,α>0° ,
∴0°<α<90°,
故选:B.
3.D
解:∵AD=CD,
∴∠DAC=∠DCA,
∵∠BAD=∠BCD,
∴∠BAD+∠DAC=∠BCD+∠DCA,
即∠BAC=∠BCA,
∴AB=BC,故①错误;
∵AD=CD,
∴∠DAC=∠DCA,
故②正确;
∵AB=BC,AD=DC,
∴BD垂直平分AC,故④正确;
∴BD平分∠ABC,故③正确;
故其中正确的有②③④,
故选:D.
4.B
解:①若AB为等腰三角形的腰,则BC即为底边,
由题意:AB=2BC,
∴2AB+BC=40,即:5BC=40,
解得:BC=8,
∴AB=16,
此时,等腰三角形三边为:16、16、8,满足三角形的三边关系,符合题意;
②若AB为等腰三角形的底边,则BC即为腰,
由题意:AB=2BC,
∴2BC+AB=40,即:2AB=40,
解得:AB=20,
∴BC=10,
此时,等腰三角形三边为:10、10、20,
但是10+10=20,不满足三角形的三边关系,不符合题意,舍去;
∴AB的长为16,
故选:B.
5.C
解:如图所示,以B为圆心,以AB的长为半径画弧与直线l交于点D,此时AB=BD,同理以A为圆心以AB的长为半径与直线l交于E、C,此时AC=AB,AE=AB,再作AB的垂直平分线与直线l交于点F,此时AF=BF,
∴一共有4个点满足题意,
故选C.
6.C
解:∵AB=AC,∠A=40°,
∴∠DBE=∠C=(180°﹣40°)=70°,
在△DBE和△BCF中,
,
∴△DBE≌△BCF(SAS),
∴∠BDE=∠CBF,
∴∠DGF=∠DBG+∠BDE=∠DBG+∠CBF=∠DBE=70°,
故选:C.
7.A
解:,
,
.
故选A.
8.B
解:∵AC=BC
∴∠B=∠A=40゜
∴∠ACB=180゜-2∠A=100゜
由尺规作图知,CF是∠ACB的平分线
∴∠BCG=
故选:B.
9.C
解:∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=BC AD=×4×AD=12,
解得:AD=6(cm),
∵EF是线段AB的垂直平分线,
∴AM=BM,
∴BM+MD=AM+DM=AD=6(cm),
故选:C.
10.D
解:∵AB=AC,BE=CE,
∴AE⊥BC,
故工程人员这种操作方法的依据是等腰三角形“三线合一”,
故选:D.
11.B
解:∵折叠,
∴AD=DF,
∵D是AB边上的中点,
∴AD=BD,
∴BD=DF,
∵∠B=50°,
∴∠DFB=∠B=50°,
∴∠BDF=180°﹣∠B﹣∠DFB=80°.
故选:B.
12.A
解:∵∠ACB=∠DCE,
∴∠ACB+∠ACD=∠DCE+∠ACD,
∴∠BCD=∠ACE,
又∵CA=CB,CD=CE,
∴△BCD≌△ACE(SAS),
∴∠GBC=∠FAC,AE=BD,
故③正确,
又∵∠BGC=∠AFC,CA=CB,
∴△BCG≌△ACF(AAS)
∴CG=CF,AF=BG,
故②正确,
∴BD-BG=AE-AF,
即DG=EF,
故①正确,
∵AC=BC,CD=CE,
AC+CD=BC+CE=BE,
∵BE不一定等于AE
故④错误,
综上所述,①②③正确,
故选:A.
13.2
解:如下图:
延长交于,
∵平分,,
∴,
∴,,
∴.
故答案:2
14.10
解:∵AB=AC,AD=AE,
∴∠B=∠C,∠ADE=∠AED,
∵∠EDC+∠C=∠AED,
∴∠C+∠EDC=∠ADE,
又∵∠B+∠BAD=∠ADC,
∴∠B+20°=∠C+∠EDC+∠EDC,
∵∠B=∠C.
∴2∠EDC=20°,
∴∠EDC=10°.
故答案为:10.
15.20°
解:∵∠BAC=80°,
∴∠B+∠C=180°-∠BAC=100°,
∵DE、GF分别是AB、AC边的垂直平分线,
∴BE=AE,AF=CF,
∴∠B=∠BAE,∠C=∠FAC,
∴∠BAE+∠FAC=100°,
∵∠BAC=80°,
∴∠FAE=∠BAE+∠FAC-∠BAC=100°-80°=20°,
故答案为:20°.
16.200
解:过点B作BE⊥DC交DC的延长线于点E,
∵BE⊥CE,
∴∠BEC=∠CDA=90°,
∴∠CBE+∠BCE=90°,
又∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
∴∠CBE=∠ACD,
在 ACD与 CBE中,
∵,
∴ ACD CBE(AAS),
∴BE=CD=20,
∴的面积=CD BE=×20×20=200,
故答案是200.
17.25°
解:如图,连接,
∠1是△的外角,
∠1 = ∠ +∠,
∠2是△的外角,
∠2 =∠ +∠,
∠1 +∠2 =∠DBE+∠,
将△BDE沿DE翻折得到△,
∠DBE=∠,
∠1 +∠2 = 2∠DBE = 80°,
∠DBE = 40°,
BA= BC,
∠BAC= ∠ACB = 70°,
AD = AF,
∠1 = ∠AFD= 55°,
∠2= 80°-∠1 = 80°- 55°= 25°,
故答案为:25°.
18.证明见解析
解:CDAB,
∠BDC= 90°,
∠BCD+∠CBD= 90°,
∠A +∠CBD = 90°,
∠BCD =∠A,
CE是∠ACD的角平分线,
∠ACE=∠DCE,
∠BEC=∠ACE +∠A =∠DCE +∠BCD,
∠BEC =∠BCE,
BC = BE,
,
EF= CF.
19.(1)见解析;(2)
解:(1)过点作于点,
即
(2)设
,,
∴AE=CE,
又
20.(1)15cm;(2)见解析
解:(1)∵MN是线段AB的垂直平分线,
∴DA=DB,
∵△BCD的周长等于26cm,
∴BC+CD+BD=26(cm),
∴BC+CD+DA=BC+AC=26(cm),
∵BC=11cm,
∴AC=15(cm),
(2)∵DA=DB,,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∴
21.(1)见详解;(2),理由见详解;(3)
解:(1)∵,,
∴,
∵,
∴,
∴,
∴,
∵,,
∴;
(2)解:,理由如下:
由(1)可得,
∴,
∵,,
∴,
∵,
∴,
∴;
(3)解:过点F作FM⊥FA交AC于点M,如图2所示:
∵,
∴△AFM是等腰直角三角形,
∴,
∴,
∴,
∵,
∴,
∴,
∴△ADF≌△MCF(ASA),
∴,
∴是等腰直角三角形,
∴.
一、单选题
1.已知等腰三角形两边的长分别为3和7,则此等腰三角形的周长为( )
A.13 B.17 C.13或17 D.13或10
2.已知在△ABC中,AB=AC,且∠B=α,则α的取值范围是( )
A.a≤45° B.0° < α < 90° C.α=90° D.90° < α < 180°
3.如图,点是内一点,,,则以下结论:①②③平分④与的位置关系是互相垂直.其中正确的有( )个
A.0 B.1 C.2 D.3
4.在等腰三角形中,AB的长是BC的2倍,周长为40,则AB的长为( )
A.20 B.16 C.16或20 D.以上都不对
5.已知:如图,经过线段一端点A有一直线l,直线上l存在点C,使为等腰三角形,这样的点C有( )个.
A.2 B.3 C.4 D.5
6.如图,在等腰△ABC中,AB=AC,点D、E、F分别是边AB、BC、CA上的点,DE与BF相交于点G,BD=BC,BE=CF,若∠A=40°,则∠DGF的度数为( )
A.40° B.60° C.70° D.110°
7.如图,在中,,,则( )
A. B.
C. D.
8.如图,在中,,,观察图中尺规作图的痕迹,可知的度数为( )
A.40° B.50° C.55° D.60°
9.如图,等腰底边的长为,面积是,为边上的中点,腰的垂直平分线交于,交于点,则的值为( )
A. B. C. D.
10.如图,为了让电线杆垂直于地面,工程人员的操作方法是:从电线杆DE上一点A往地面拉两条长度相等的固定绳AB与AC,当固定点B,C到杆脚E的距离相等,且B,EC在同一直线上时,电线杆DE就垂直于BC工程人员这种操作方法的依据是( )
A.等边对等角 B.等角对等边
C.垂线段最短 D.等腰三角形“三线合一”
11.如图,D是AB边上的中点,将ABC沿过D点的直线折叠,使点A落在BC上F处,若∠B=50°,则∠BDF的大小为( )
A.50° B.80° C.90° D.100°
12.如图,点B、C、E、在同一直线上,△ABC与△CDE为等腰三角形,CA=CB,CD=CE,∠ACB=∠DCE,∠BGC=∠AFC,则下列结论:①DG=EF;②CG=CF;③AE=BD;④AC+CD=AE.正确的有( )
A.3个 B.2个 C.1个 D.0个
二、填空题
13.如图,△ABC的面积为4cm2,BP平分∠ABC,且AP⊥BP于点P,则△PBC的面积为______cm2
14.如图,AB=AC,AD=AE,∠BAD=20°,则∠CDE度数是_______度.
15.如图,在△ABC中,∠BAC=80°,DE,FG分别是AB,AC边的垂直平分线,点E、F在BC上,则∠FAE的度数为__________.
16.如图,在四边形中,,,,则的面积为__________.
17.如图,△ABC为等腰三角形,AB=BC,点D、E分别为AB、BC上的两点,将△BDE沿DE翻折得到ΔB′DE,DB′交AC于点F,若∠1+∠2=80°,AD=AF,则∠2=___.
三、解答题
18.如图,中,是的角平分线,,求证:.
19.如图,已知点、在△ABC的边上,,.
(1)求证:;
(2)若,求的度数.
20.如图,在中,的垂直平分线交于点,交于点,且,的周长等于26cm.
(1)求的长.
(2)若,且,求证:.
21.如图,已知四边形,连接,其中,,,延长到点,得,点为上一点,连接、,交于点.
(1)求证:;
(2)若,,试探究、的数量关系,并说明理由;
(3)如图2,连接,若,求的度数.
参考答案
1.B
解:①当腰是3,底边是7时,3+3<7不满足三角形的三边关系,因此舍去.
②当底边是3,腰长是7时,7+7>3能构成三角形,则其周长=3+7+7=17.
故选:B.
2.B
解:∵在△ABC中,AB=AC,∠B=α,
∴∠B=∠C=α,
∵三角形内角和∠A+∠B+∠C=180°,
∴∠B+∠C<180°,
即:2α<180°,
∴α<90°,
又由题意可知,α>0° ,
∴0°<α<90°,
故选:B.
3.D
解:∵AD=CD,
∴∠DAC=∠DCA,
∵∠BAD=∠BCD,
∴∠BAD+∠DAC=∠BCD+∠DCA,
即∠BAC=∠BCA,
∴AB=BC,故①错误;
∵AD=CD,
∴∠DAC=∠DCA,
故②正确;
∵AB=BC,AD=DC,
∴BD垂直平分AC,故④正确;
∴BD平分∠ABC,故③正确;
故其中正确的有②③④,
故选:D.
4.B
解:①若AB为等腰三角形的腰,则BC即为底边,
由题意:AB=2BC,
∴2AB+BC=40,即:5BC=40,
解得:BC=8,
∴AB=16,
此时,等腰三角形三边为:16、16、8,满足三角形的三边关系,符合题意;
②若AB为等腰三角形的底边,则BC即为腰,
由题意:AB=2BC,
∴2BC+AB=40,即:2AB=40,
解得:AB=20,
∴BC=10,
此时,等腰三角形三边为:10、10、20,
但是10+10=20,不满足三角形的三边关系,不符合题意,舍去;
∴AB的长为16,
故选:B.
5.C
解:如图所示,以B为圆心,以AB的长为半径画弧与直线l交于点D,此时AB=BD,同理以A为圆心以AB的长为半径与直线l交于E、C,此时AC=AB,AE=AB,再作AB的垂直平分线与直线l交于点F,此时AF=BF,
∴一共有4个点满足题意,
故选C.
6.C
解:∵AB=AC,∠A=40°,
∴∠DBE=∠C=(180°﹣40°)=70°,
在△DBE和△BCF中,
,
∴△DBE≌△BCF(SAS),
∴∠BDE=∠CBF,
∴∠DGF=∠DBG+∠BDE=∠DBG+∠CBF=∠DBE=70°,
故选:C.
7.A
解:,
,
.
故选A.
8.B
解:∵AC=BC
∴∠B=∠A=40゜
∴∠ACB=180゜-2∠A=100゜
由尺规作图知,CF是∠ACB的平分线
∴∠BCG=
故选:B.
9.C
解:∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=BC AD=×4×AD=12,
解得:AD=6(cm),
∵EF是线段AB的垂直平分线,
∴AM=BM,
∴BM+MD=AM+DM=AD=6(cm),
故选:C.
10.D
解:∵AB=AC,BE=CE,
∴AE⊥BC,
故工程人员这种操作方法的依据是等腰三角形“三线合一”,
故选:D.
11.B
解:∵折叠,
∴AD=DF,
∵D是AB边上的中点,
∴AD=BD,
∴BD=DF,
∵∠B=50°,
∴∠DFB=∠B=50°,
∴∠BDF=180°﹣∠B﹣∠DFB=80°.
故选:B.
12.A
解:∵∠ACB=∠DCE,
∴∠ACB+∠ACD=∠DCE+∠ACD,
∴∠BCD=∠ACE,
又∵CA=CB,CD=CE,
∴△BCD≌△ACE(SAS),
∴∠GBC=∠FAC,AE=BD,
故③正确,
又∵∠BGC=∠AFC,CA=CB,
∴△BCG≌△ACF(AAS)
∴CG=CF,AF=BG,
故②正确,
∴BD-BG=AE-AF,
即DG=EF,
故①正确,
∵AC=BC,CD=CE,
AC+CD=BC+CE=BE,
∵BE不一定等于AE
故④错误,
综上所述,①②③正确,
故选:A.
13.2
解:如下图:
延长交于,
∵平分,,
∴,
∴,,
∴.
故答案:2
14.10
解:∵AB=AC,AD=AE,
∴∠B=∠C,∠ADE=∠AED,
∵∠EDC+∠C=∠AED,
∴∠C+∠EDC=∠ADE,
又∵∠B+∠BAD=∠ADC,
∴∠B+20°=∠C+∠EDC+∠EDC,
∵∠B=∠C.
∴2∠EDC=20°,
∴∠EDC=10°.
故答案为:10.
15.20°
解:∵∠BAC=80°,
∴∠B+∠C=180°-∠BAC=100°,
∵DE、GF分别是AB、AC边的垂直平分线,
∴BE=AE,AF=CF,
∴∠B=∠BAE,∠C=∠FAC,
∴∠BAE+∠FAC=100°,
∵∠BAC=80°,
∴∠FAE=∠BAE+∠FAC-∠BAC=100°-80°=20°,
故答案为:20°.
16.200
解:过点B作BE⊥DC交DC的延长线于点E,
∵BE⊥CE,
∴∠BEC=∠CDA=90°,
∴∠CBE+∠BCE=90°,
又∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
∴∠CBE=∠ACD,
在 ACD与 CBE中,
∵,
∴ ACD CBE(AAS),
∴BE=CD=20,
∴的面积=CD BE=×20×20=200,
故答案是200.
17.25°
解:如图,连接,
∠1是△的外角,
∠1 = ∠ +∠,
∠2是△的外角,
∠2 =∠ +∠,
∠1 +∠2 =∠DBE+∠,
将△BDE沿DE翻折得到△,
∠DBE=∠,
∠1 +∠2 = 2∠DBE = 80°,
∠DBE = 40°,
BA= BC,
∠BAC= ∠ACB = 70°,
AD = AF,
∠1 = ∠AFD= 55°,
∠2= 80°-∠1 = 80°- 55°= 25°,
故答案为:25°.
18.证明见解析
解:CDAB,
∠BDC= 90°,
∠BCD+∠CBD= 90°,
∠A +∠CBD = 90°,
∠BCD =∠A,
CE是∠ACD的角平分线,
∠ACE=∠DCE,
∠BEC=∠ACE +∠A =∠DCE +∠BCD,
∠BEC =∠BCE,
BC = BE,
,
EF= CF.
19.(1)见解析;(2)
解:(1)过点作于点,
即
(2)设
,,
∴AE=CE,
又
20.(1)15cm;(2)见解析
解:(1)∵MN是线段AB的垂直平分线,
∴DA=DB,
∵△BCD的周长等于26cm,
∴BC+CD+BD=26(cm),
∴BC+CD+DA=BC+AC=26(cm),
∵BC=11cm,
∴AC=15(cm),
(2)∵DA=DB,,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∴
21.(1)见详解;(2),理由见详解;(3)
解:(1)∵,,
∴,
∵,
∴,
∴,
∴,
∵,,
∴;
(2)解:,理由如下:
由(1)可得,
∴,
∵,,
∴,
∵,
∴,
∴;
(3)解:过点F作FM⊥FA交AC于点M,如图2所示:
∵,
∴△AFM是等腰直角三角形,
∴,
∴,
∴,
∵,
∴,
∴,
∴△ADF≌△MCF(ASA),
∴,
∴是等腰直角三角形,
∴.
