2.1.1直线的斜率和倾斜角 课件(共23张PPT)
文档属性
| 名称 | 2.1.1直线的斜率和倾斜角 课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-18 10:48:38 | ||
图片预览





文档简介
(共23张PPT)
2.1.1直线的斜率和倾斜角
人教A(2019)版
选择性必修一
新知导入
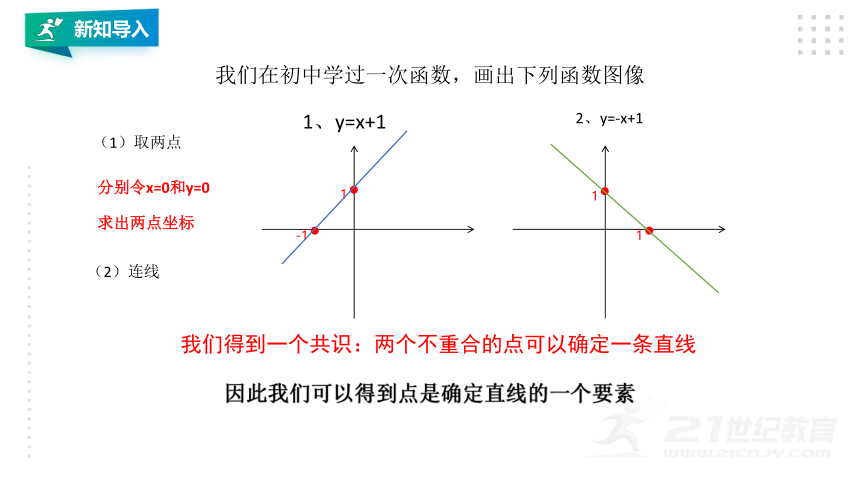
我们在初中学过一次函数,画出下列函数图像
1、y=x+1
2、y=-x+1
(1)取两点
(2)连线
分别令x=0和y=0
求出两点坐标
1
-1
1
1
我们得到一个共识:两个不重合的点可以确定一条直线
因此我们可以得到点是确定直线的一个要素
新知导入
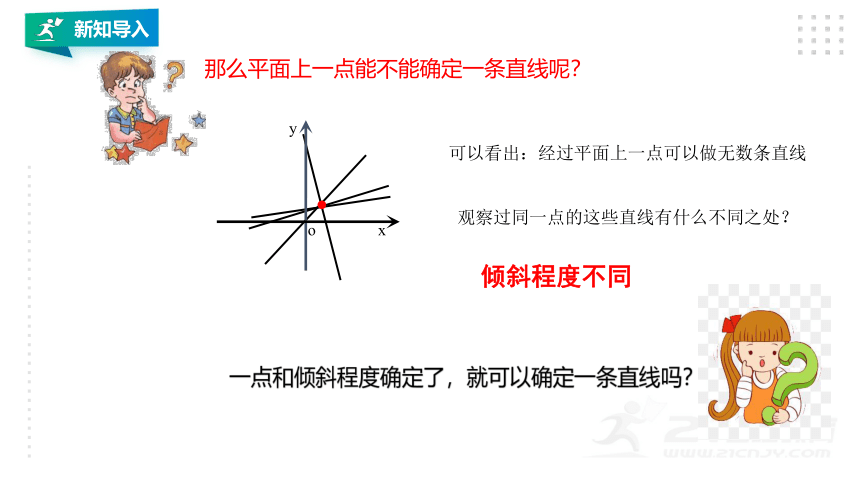
那么平面上一点能不能确定一条直线呢?
.
y
x
o
可以看出:经过平面上一点可以做无数条直线
观察过同一点的这些直线有什么不同之处?
倾斜程度不同
一点和倾斜程度确定了,就可以确定一条直线吗?
新知导入
1、经过原点的直线有多少条?
经过原点的直线有无数条
2、与x轴正方向所成的角为300的直线有多少条?
与x轴正方向所成的角为300的直线有无数条
3、经过原点的直线并与x轴正方向所成的角为300的直线有多少条?
这样的直线有且只有一条
倾斜程度用什么量来刻画呢?
新知讲解
倾斜角的定义
当直线l与x轴相交时,我们取x轴作为基准,x轴正向与直线l向上
方向之间所成的角叫做直线的倾斜角。
P
l2
l1
l3
1
2
3
x
y
O
l
规定:当直线l与x轴平行或重合时,其倾斜角为00
l
这条呢?
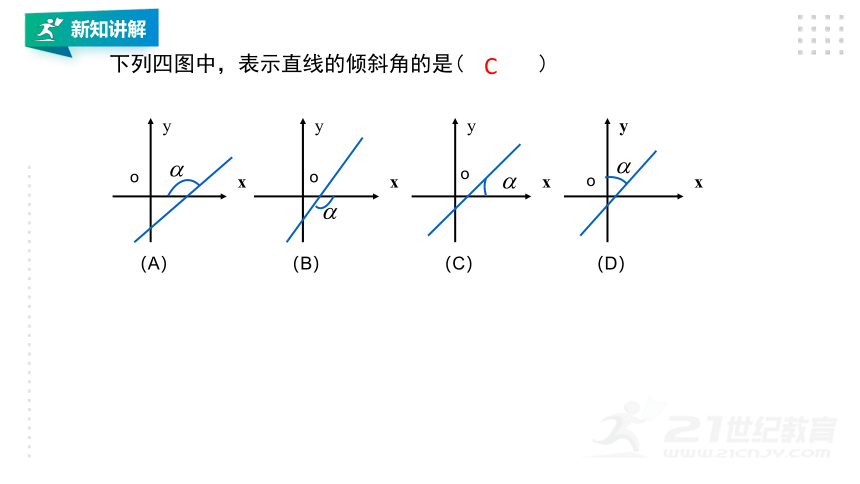
下列四图中,表示直线的倾斜角的是( )
x
y
o
x
y
o
x
y
o
x
y
o
(A)
(B)
(C)
(D)
C
新知讲解
倾斜角的取值范围
新知讲解
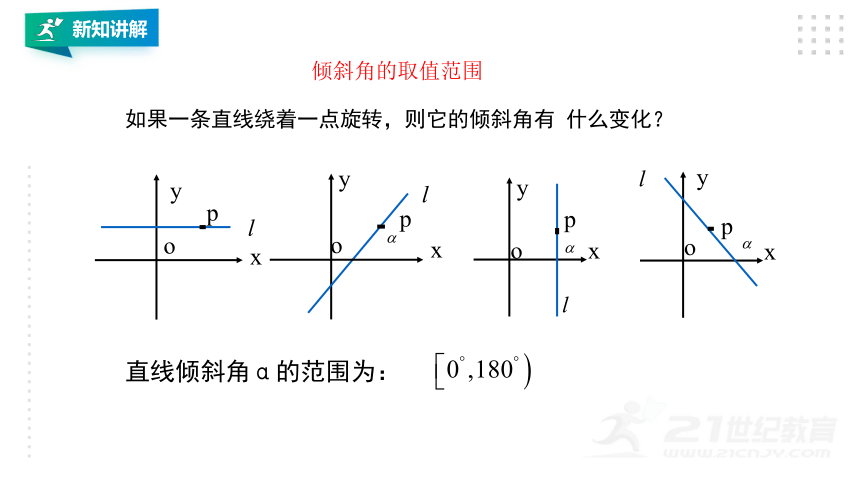
如果一条直线绕着一点旋转,则它的倾斜角有 什么变化?
p
o
y
x
y
p
o
x
p
o
y
x
p
o
y
x
直线倾斜角α的范围为:
你认为下列说法对吗?
1、所有的直线都有唯一确定的倾斜角与它对应。
P
l2
l1
l3
1
2
3
对
2、每一个倾斜角都对应于唯一的一条直线。
错
合作探究
新知讲解
下面我们进一步研究刻画直线倾斜程度的方法
坡角
坡角
坡角
坡角
坡度=
高度
宽度
(坡度越大,楼梯越陡)
新知讲解
类比坡度来刻画直线的倾斜程度
级宽
高级
高度
宽度
直线
x
y
o
P1(x1,y1)
P2(x2,y2)
M
直线的倾斜程度=
MP1
P2M
新知讲解
下面我们利用向量来探讨倾斜角和P、Q两点坐标的关系
1、已知直线l过点O(0,0)和 ,α和O、P的坐标有什么关系?
向量
直线OP的倾斜角为α ,
由正切函数定义:
2、如果直线l经过P1(-1,1) ,
α与P1,P2坐标有什么关系呢?
P1(-1,1)
●
●
α
α
P
向量
平移向量 到 ,
则点P的坐标
直线OP的倾斜角也是α
由正切函数的定义:
新知讲解
3、如果直线l经过P1(x1,y1) ,P2(x2,y2),且x1≠x2,则α与P1、P2的坐标什么关系呢?
由1、2容易得到
定义:我们把一条直线的的倾斜角的正切值叫做
这条直线的斜率。斜率通常用k表示,即:
注:倾斜角是90 °的直线斜率不存在。
新知讲解
由倾斜解的取值范围,我们得出斜率的取值范围
2
3
2
o
2
-
y
x
斜率k不存在
k的取值范围(-∞,+∞)
新知讲解
斜率的正负与倾斜角大小的关系
p
o
y
x
p
o
y
x
p
o
y
x
y
p
o
x
0°< < 90°
= 90°
90°< <180°
= 0°
零度角
锐角
直角
钝角
k不存在
k>0
k<0
k=0
新知讲解
例1 如图 ,已知 ,求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
解:直线AB的斜率
直线BC的斜率
直线CA的斜率
由 及 知,直线AB 与CA的倾斜角均为锐角;
由 知,直线BC的倾斜角为钝角.
合作探究
例2 在平面直角坐标系中,画出经过原点且斜率为1的直线 .
x
y
解:取 上某一点为 的坐标是 ,根据斜率公
式有:
即
设 ,则 ,于是 的坐标是 过原点及 的直线即为 .
A
课堂练习
1、判断正误:
③任一条直线都有倾斜角,所以任一条直线都有斜率( )
①直线的倾斜角为α,则直线的斜率为 ( )
④直线的倾斜角越大,则直线的斜率越大 ( )
⑤两直线的倾斜角相等,则它们的斜率也相等 ( )
⑥平行于x轴的直线的倾斜角是 ( )
②直线的斜率的范围是 ( )
×
×
×
×
×
2、如图,直线的斜率分别为,则( )
X
Y
O
A.
B.
C.
D.
C
课堂练习
课堂总结
1.直线的倾斜角的定义
2.直线的斜率的定义
3.两点间斜率公式
板书设计
1、直线的倾斜角定义:
3、直线的斜率定义:
4、过两点的直线的斜率公式:
2、倾斜角范围:
5、直线的斜率取值范围:
当直线l与x轴相交时,我们取x轴作为基准,x轴正向与直线l向上方向之间所成的角叫做直线的倾斜角。
作业布置
2、已知下列直线的倾斜角,求直线的斜率.
3、如果直线l经过点A(3,4),B(x,y),且斜率k=2,你能说出x,y的关系吗?
4、课本P552、3、4、5
https://www.21cnjy.com/help/help_extract.php
2.1.1直线的斜率和倾斜角
人教A(2019)版
选择性必修一
新知导入
我们在初中学过一次函数,画出下列函数图像
1、y=x+1
2、y=-x+1
(1)取两点
(2)连线
分别令x=0和y=0
求出两点坐标
1
-1
1
1
我们得到一个共识:两个不重合的点可以确定一条直线
因此我们可以得到点是确定直线的一个要素
新知导入
那么平面上一点能不能确定一条直线呢?
.
y
x
o
可以看出:经过平面上一点可以做无数条直线
观察过同一点的这些直线有什么不同之处?
倾斜程度不同
一点和倾斜程度确定了,就可以确定一条直线吗?
新知导入
1、经过原点的直线有多少条?
经过原点的直线有无数条
2、与x轴正方向所成的角为300的直线有多少条?
与x轴正方向所成的角为300的直线有无数条
3、经过原点的直线并与x轴正方向所成的角为300的直线有多少条?
这样的直线有且只有一条
倾斜程度用什么量来刻画呢?
新知讲解
倾斜角的定义
当直线l与x轴相交时,我们取x轴作为基准,x轴正向与直线l向上
方向之间所成的角叫做直线的倾斜角。
P
l2
l1
l3
1
2
3
x
y
O
l
规定:当直线l与x轴平行或重合时,其倾斜角为00
l
这条呢?
下列四图中,表示直线的倾斜角的是( )
x
y
o
x
y
o
x
y
o
x
y
o
(A)
(B)
(C)
(D)
C
新知讲解
倾斜角的取值范围
新知讲解
如果一条直线绕着一点旋转,则它的倾斜角有 什么变化?
p
o
y
x
y
p
o
x
p
o
y
x
p
o
y
x
直线倾斜角α的范围为:
你认为下列说法对吗?
1、所有的直线都有唯一确定的倾斜角与它对应。
P
l2
l1
l3
1
2
3
对
2、每一个倾斜角都对应于唯一的一条直线。
错
合作探究
新知讲解
下面我们进一步研究刻画直线倾斜程度的方法
坡角
坡角
坡角
坡角
坡度=
高度
宽度
(坡度越大,楼梯越陡)
新知讲解
类比坡度来刻画直线的倾斜程度
级宽
高级
高度
宽度
直线
x
y
o
P1(x1,y1)
P2(x2,y2)
M
直线的倾斜程度=
MP1
P2M
新知讲解
下面我们利用向量来探讨倾斜角和P、Q两点坐标的关系
1、已知直线l过点O(0,0)和 ,α和O、P的坐标有什么关系?
向量
直线OP的倾斜角为α ,
由正切函数定义:
2、如果直线l经过P1(-1,1) ,
α与P1,P2坐标有什么关系呢?
P1(-1,1)
●
●
α
α
P
向量
平移向量 到 ,
则点P的坐标
直线OP的倾斜角也是α
由正切函数的定义:
新知讲解
3、如果直线l经过P1(x1,y1) ,P2(x2,y2),且x1≠x2,则α与P1、P2的坐标什么关系呢?
由1、2容易得到
定义:我们把一条直线的的倾斜角的正切值叫做
这条直线的斜率。斜率通常用k表示,即:
注:倾斜角是90 °的直线斜率不存在。
新知讲解
由倾斜解的取值范围,我们得出斜率的取值范围
2
3
2
o
2
-
y
x
斜率k不存在
k的取值范围(-∞,+∞)
新知讲解
斜率的正负与倾斜角大小的关系
p
o
y
x
p
o
y
x
p
o
y
x
y
p
o
x
0°< < 90°
= 90°
90°< <180°
= 0°
零度角
锐角
直角
钝角
k不存在
k>0
k<0
k=0
新知讲解
例1 如图 ,已知 ,求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
解:直线AB的斜率
直线BC的斜率
直线CA的斜率
由 及 知,直线AB 与CA的倾斜角均为锐角;
由 知,直线BC的倾斜角为钝角.
合作探究
例2 在平面直角坐标系中,画出经过原点且斜率为1的直线 .
x
y
解:取 上某一点为 的坐标是 ,根据斜率公
式有:
即
设 ,则 ,于是 的坐标是 过原点及 的直线即为 .
A
课堂练习
1、判断正误:
③任一条直线都有倾斜角,所以任一条直线都有斜率( )
①直线的倾斜角为α,则直线的斜率为 ( )
④直线的倾斜角越大,则直线的斜率越大 ( )
⑤两直线的倾斜角相等,则它们的斜率也相等 ( )
⑥平行于x轴的直线的倾斜角是 ( )
②直线的斜率的范围是 ( )
×
×
×
×
×
2、如图,直线的斜率分别为,则( )
X
Y
O
A.
B.
C.
D.
C
课堂练习
课堂总结
1.直线的倾斜角的定义
2.直线的斜率的定义
3.两点间斜率公式
板书设计
1、直线的倾斜角定义:
3、直线的斜率定义:
4、过两点的直线的斜率公式:
2、倾斜角范围:
5、直线的斜率取值范围:
当直线l与x轴相交时,我们取x轴作为基准,x轴正向与直线l向上方向之间所成的角叫做直线的倾斜角。
作业布置
2、已知下列直线的倾斜角,求直线的斜率.
3、如果直线l经过点A(3,4),B(x,y),且斜率k=2,你能说出x,y的关系吗?
4、课本P552、3、4、5
https://www.21cnjy.com/help/help_extract.php
