2021-2022学年青岛版九年级数学上册第2章解直角三角形 同步达标测评(word版含答案)
文档属性
| 名称 | 2021-2022学年青岛版九年级数学上册第2章解直角三角形 同步达标测评(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 346.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-15 22:31:00 | ||
图片预览



文档简介
2021-2022学年青岛版九年级数学上册《第2章解直角三角形》同步达标测评2(附答案)
一.选择题(共10小题,满分30分)
1.在Rt△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边,下列等式中,正确的是( )
A. B. C. D.
2.三角函数sin30°、cos16°、cos43°之间的大小关系是( )
A.cos43°>cos16°>sin30° B.cos16°>sin30°>cos43°
C.cos16°>cos43°>sin30° D.cos43°>sin30°>cos16°
3.如果α是锐角,且sinα=,那么cos(90°﹣α)的值为( )
A. B. C. D.
4.在Rt△ABC中,∠C=90°,如果sinA=,那么sinB的值是( )
A. B. C. D.3
5.cos30°的相反数是( )
A. B. C. D.
6.如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )
A.5÷tan26°= B.5÷sin26°= C.5×cos26°= D.5×tan26°=
7.如图,若△ABC和△DEF的面积分别为S1,S2,则( )
A.S1=S2 B.S1=S2 C.S1=S2 D.S1=S2
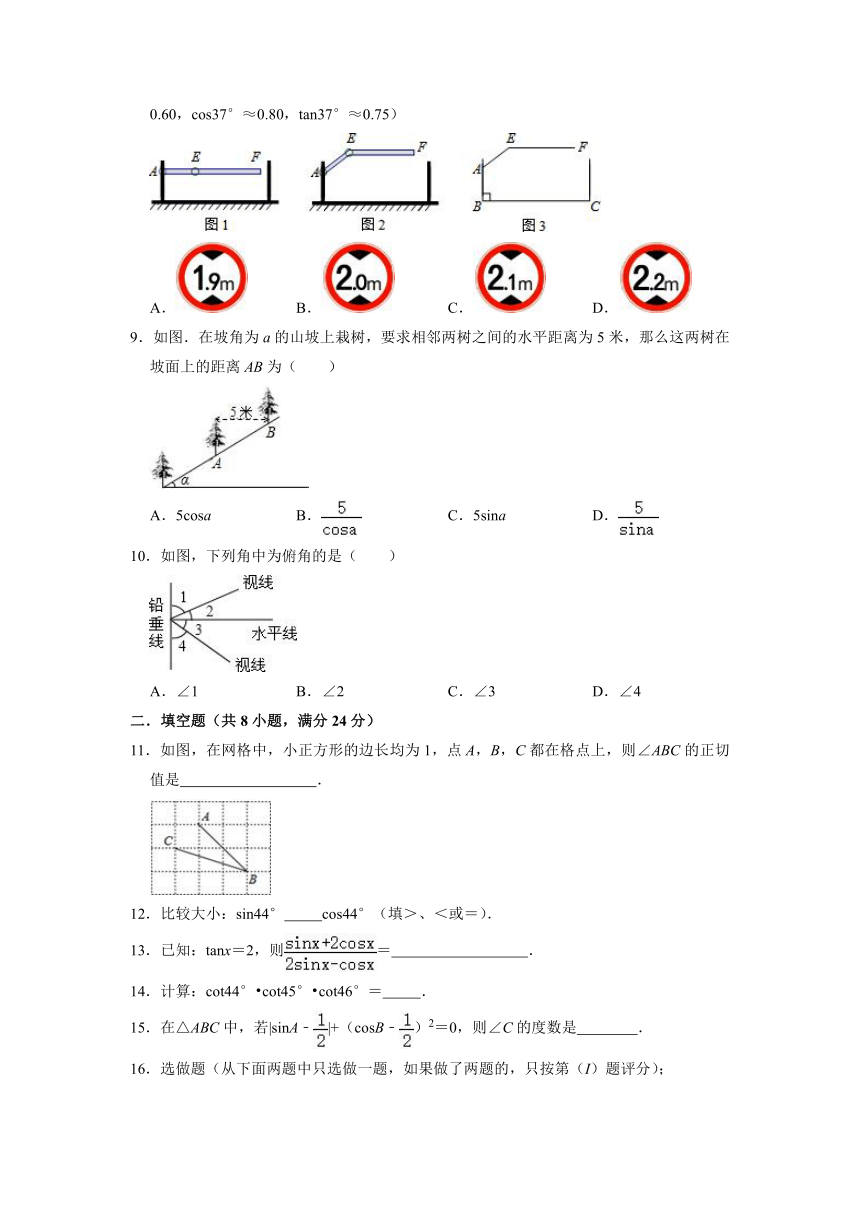
8.某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A. B. C. D.
9.如图.在坡角为a的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为( )
A.5cosa B. C.5sina D.
10.如图,下列角中为俯角的是( )
A.∠1 B.∠2 C.∠3 D.∠4
二.填空题(共8小题,满分24分)
11.如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是 .
12.比较大小:sin44° cos44°(填>、<或=).
13.已知:tanx=2,则= .
14.计算:cot44° cot45° cot46°= .
15.在△ABC中,若|sinA﹣|+(cosB﹣)2=0,则∠C的度数是 .
16.选做题(从下面两题中只选做一题,如果做了两题的,只按第(I)题评分);
(Ⅰ)计算:= .
(Ⅱ)用“>”或“<”号填空: 0.(可用计算器计算)
17.如图,点A(2,2),N(1,0),∠AON=60°,点M为平面直角坐标系内一点,且MO=MA,则MN的最小值为 .
18.根据爱因斯坦的相对论可知,任何物体的运动速度不能超过光速(3×105km/s),因为一个物体达到光速需要无穷多的能量,并且时光会倒流,这在现实中是不可能的.但我们可让一个虚拟物超光速运动,例如:直线l,m表示两条木棒相交成的锐角的度数为10°,它们分别以与自身垂直的方向向两侧平移时,它们的交点A也随着移动(如图箭头所示),如果两条直线的移动速度都是光速的0.2倍,则交点A的移动速度是光速的 倍.(结果保留两个有效数字).
三.解答题(共8小题,满分66分)
19.在△ABC中,∠B、∠C 均为锐角,其对边分别为b、c,求证:=.
20.下列关系式是否成立(0<α<90°),请说明理由.
(1)sinα+cosα≤1;
(2)sin2α=2sinα.
21.计算:+()﹣1﹣4cos45°﹣()0.
22.如图,在△ABC中,∠A=30°,cosB=,AC=6.求AB的长.
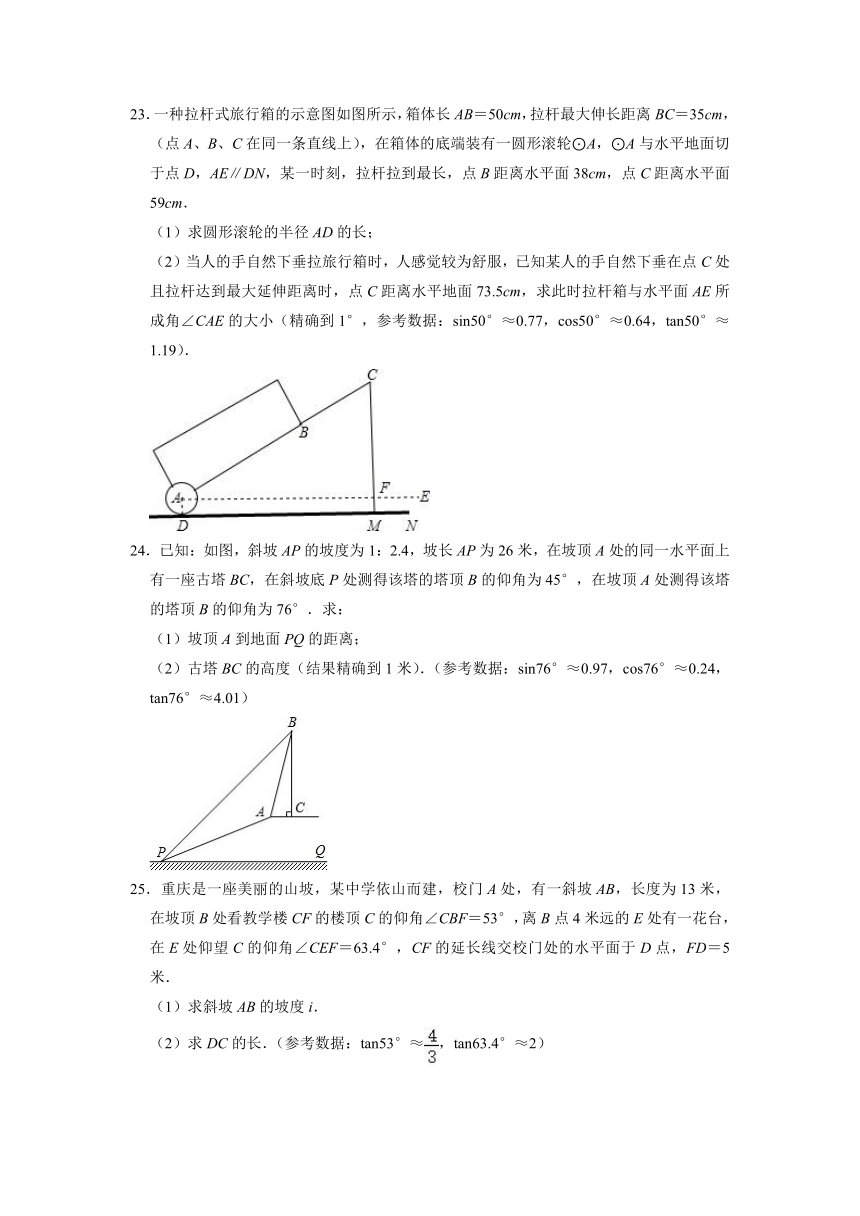
23.一种拉杆式旅行箱的示意图如图所示,箱体长AB=50cm,拉杆最大伸长距离BC=35cm,(点A、B、C在同一条直线上),在箱体的底端装有一圆形滚轮⊙A,⊙A与水平地面切于点D,AE∥DN,某一时刻,拉杆拉到最长,点B距离水平面38cm,点C距离水平面59cm.
(1)求圆形滚轮的半径AD的长;
(2)当人的手自然下垂拉旅行箱时,人感觉较为舒服,已知某人的手自然下垂在点C处且拉杆达到最大延伸距离时,点C距离水平地面73.5cm,求此时拉杆箱与水平面AE所成角∠CAE的大小(精确到1°,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19).
24.已知:如图,斜坡AP的坡度为1:2.4,坡长AP为26米,在坡顶A处的同一水平面上有一座古塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角为76°.求:
(1)坡顶A到地面PQ的距离;
(2)古塔BC的高度(结果精确到1米).(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
25.重庆是一座美丽的山坡,某中学依山而建,校门A处,有一斜坡AB,长度为13米,在坡顶B处看教学楼CF的楼顶C的仰角∠CBF=53°,离B点4米远的E处有一花台,在E处仰望C的仰角∠CEF=63.4°,CF的延长线交校门处的水平面于D点,FD=5米.
(1)求斜坡AB的坡度i.
(2)求DC的长.(参考数据:tan53°≈,tan63.4°≈2)
26.如图,海中有一小岛P,在距小岛P的海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?
参考答案
一.选择题(共10小题,满分30分)
1.解:根据三角函数的定义:
A、sinA=,错误;
B、cosB=,错误;
C、tanA=,正确;
D、cotB=,错误.
故选:C.
2.解:∵sin30°=cos60°,
又16°<43°<60°,余弦值随着角度的增大而减小,
∴cos16°>cos43°>sin30°.
故选:C.
3.解:∵α为锐角,,
∴cos(90°﹣α)=sinα=.
故选:B.
4.解:∵Rt△ABC中,∠C=90°,sinA=,
∴cosA===,
∴∠A+∠B=90°,
∴sinB=cosA=.
故选:A.
5.解:∵cos30°=,
∴它的相反数为﹣.
故选:C.
6.解:由tan∠B=,得
AC=BC tanB=5×tan26°.
故选:D.
7.解:作AM⊥BC于M,DN⊥EF于N,如图,
在Rt△ABM中,∵sin∠B=,
∴AM=3sin50°,
∴S1=BC AM=×7×3sin50°=sin50°,
在Rt△DEN中,∠DEN=180°﹣130°=50°,
∵sin∠DEN=,
∴DN=7sin50°,
∴S2=EF DN=×3×7sin50°=sin50°,
∴S1=S2.
故选:D.
8.解:如图,过点A作BC的平行线AG,过点E作EH⊥AG于H,
则∠EHG=∠HEF=90°,
∵∠AEF=143°,
∴∠AEH=∠AEF﹣∠HEF=53°,
∠EAH=37°,
在△EAH中,∠EHA=90°,∠EAH=37°,AE=1.2米,
∴EH=AE sin∠EAH≈1.2×0.60=0.72(米),
∵AB=1.2米,
∴AB+EH≈1.2+0.72=1.92≈1.9米.
故选:A.
9.解:由于相邻两树之间的水平距离为5米,坡角为α,
则两树在坡面上的距离AB=.
故选:B.
10.解:根据俯角的定义,首先确定水平线,水平线以下与视线的夹角,即是俯角.
故选:C.
二.填空题(共8小题,满分24分)
11.解:连接AC,
由网格特点和正方形的性质可知,∠BAC=90°,
根据勾股定理得,AC=,AB=2,
则tan∠ABC==,
故答案为:.
12.解:∵cos44°=sin46°,正弦值随着角的增大而增大,
又∵44°<46°,
∴sin44°<cos44°.
故答案为:<.
13.解:分子分母同时除以cosx,原分式可化为:,
当tanx=2时,原式==.
故答案为:.
14.解:cot44° cot45° cot46°=cot44° cot46° cot45°=1 cot45°=1.
15.解:∵在△ABC中,|sinA﹣|+(cosB﹣)2=0,
∴sinA=,cosB=,
∴∠A=30°,∠B=60°,
∴∠C=180°﹣30°﹣60°=90°.
故答案为:90°.
16.解:(Ⅰ)sin60° cos30°﹣= ﹣=﹣=.
(Ⅱ)sin50°cos40°﹣≈0.0868>0.
故答案为:(Ⅰ).
(Ⅱ)>.
17.解:如图,过点A作AB⊥x轴,
则OB=2、AB=2,
∴OA===4,
∵cos∠AOB===,
∴∠AOB=60°,
作AO的中垂线交x轴于点P,交OA于点Q,
则OQ=AQ=2,
∴OP==4,
∵N(1,0),
∴PN=3,
∵MO=MA,
∴点M在PQ上,
当MN⊥PQ时,MN最小,
∵PQ⊥OA、PQ⊥MN,
∴MN=,
故答案为:.
18.解:如图,根据题意设光速为tm/s,
则一秒内,m与l移动的距离为0.2tm,
过A'作CA'⊥AC于A',
在Rt△ACA'中,∠A'AC1=10°÷2=5°,A'C=0.2tm,
∴AA'=CA'÷sin5°≈2.3,
∴A移动的距离约为2.3tm;
故交点A的移动速度是光速的2.3倍.
三.解答题(共8小题,满分66分)
19.证明:过A作AD⊥BC于D,
在Rt△ABD中,sinB=,
∴AD=ABsinB,
在Rt△ADC中,sinC=,
∴AD=ACsinC,
∴ABsinB=ACsinC,
而AB=c,AC=b,
∴csinB=bsinC,
∴=.
20.解:(1)该不等式不成立,理由如下:
如图,在△ABC中,∠B=90°,∠C=α.
则sinα+cosα=+=>1,故sinα+cosα≤1不成立;
(2)该等式不成立,理由如下:
假设α=30°,则sin2α=sin60°=,2sinα=2sin30°=2×=1,
∵≠1,
∴sin2α≠2sinα,即sin2α=2sinα不成立.
21.解:原式=2+2﹣4×﹣1,
=2+2﹣2﹣1,
=1.
故答案为:1.
22.解:过点C作CD⊥AB于点D.
∵∠A=30°,
∴CD=AC=3,AD=AC cosA=9,
∵cosB=,
∴设BD=4x,则BC=5x,
由勾股定理得,CD=3x,
由题意的,3x=3,
解得,x=,
∴BD=4,
∴AB=AD+BD=9+4.
23.解:(1)作BH⊥AF于点G,交DM于点H.
则BG∥CF
设圆形滚轮的半径AD的长是xcm.
则=,即=,
解得:x=8.
则圆形滚轮的半径AD的长是8cm;
(2)CF=73.5﹣8=65.5(Cm).
则sin∠CAF==≈0.77,
则∠CAF=50°.
24.解:(1)过点A作AH⊥PQ,垂足为点H.
∵斜坡AP的坡度为1:2.4,∴=,
设AH=5km,则PH=12km,
由勾股定理,得AP=13km.
∴13k=26. 解得k=2.
∴AH=10(m).
答:坡顶A到地面PQ的距离为10m.
(2)延长BC交PQ于点D.
∵BC⊥AC,AC∥PQ,
∴BD⊥PQ.
∴四边形AHDC是矩形,CD=AH=10,AC=DH.
∵∠BPD=45°,
∴PD=BD.
设BC=x,则x+10=24+DH.∴AC=DH=x﹣14.
在Rt△ABC中,tan76°=,即≈4.0,
解得x=,即x≈19,
答:古塔BC的高度约为19米.
25.解:(1)过B作BG⊥AD于G,
则四边形BGDF是矩形,
∴BG=DF=5米,
∵AB=13米,
∴AG==12米,
∴AB的坡度i==1:2.4;
(2)在Rt△BCF中,BF==,
在Rt△CEF中,EF==,
∵BE=4米,
∴BF﹣EF═﹣=4,
解得:CF=16.
∴DC=CF+DF=16+5=21米.
26.解:过P作PB⊥AM于B,
在Rt△APB中,∵∠PAB=30°,
∴PB=AP=×32=16海里,
∵16<16,
故轮船有触礁危险.
为了安全,应改变航行方向,并且保证点P到航线的距离不小于暗礁的半径16海里,即这个距离至少为16海里,
设安全航向为AC,作PD⊥AC于点D,
由题意得,AP=32海里,PD=16海里,
∵sin∠PAC===,
∴在Rt△PAD中,∠PAC=45°,
∴∠BAC=∠PAC﹣∠PAB=45°﹣30°=15°.
答:若轮船继续向正东方向航行,轮船有触礁危险.轮船自A处开始至少沿东偏南15°度方向航行,才能安全通过这一海域.
一.选择题(共10小题,满分30分)
1.在Rt△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边,下列等式中,正确的是( )
A. B. C. D.
2.三角函数sin30°、cos16°、cos43°之间的大小关系是( )
A.cos43°>cos16°>sin30° B.cos16°>sin30°>cos43°
C.cos16°>cos43°>sin30° D.cos43°>sin30°>cos16°
3.如果α是锐角,且sinα=,那么cos(90°﹣α)的值为( )
A. B. C. D.
4.在Rt△ABC中,∠C=90°,如果sinA=,那么sinB的值是( )
A. B. C. D.3
5.cos30°的相反数是( )
A. B. C. D.
6.如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )
A.5÷tan26°= B.5÷sin26°= C.5×cos26°= D.5×tan26°=
7.如图,若△ABC和△DEF的面积分别为S1,S2,则( )
A.S1=S2 B.S1=S2 C.S1=S2 D.S1=S2
8.某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A. B. C. D.
9.如图.在坡角为a的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为( )
A.5cosa B. C.5sina D.
10.如图,下列角中为俯角的是( )
A.∠1 B.∠2 C.∠3 D.∠4
二.填空题(共8小题,满分24分)
11.如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是 .
12.比较大小:sin44° cos44°(填>、<或=).
13.已知:tanx=2,则= .
14.计算:cot44° cot45° cot46°= .
15.在△ABC中,若|sinA﹣|+(cosB﹣)2=0,则∠C的度数是 .
16.选做题(从下面两题中只选做一题,如果做了两题的,只按第(I)题评分);
(Ⅰ)计算:= .
(Ⅱ)用“>”或“<”号填空: 0.(可用计算器计算)
17.如图,点A(2,2),N(1,0),∠AON=60°,点M为平面直角坐标系内一点,且MO=MA,则MN的最小值为 .
18.根据爱因斯坦的相对论可知,任何物体的运动速度不能超过光速(3×105km/s),因为一个物体达到光速需要无穷多的能量,并且时光会倒流,这在现实中是不可能的.但我们可让一个虚拟物超光速运动,例如:直线l,m表示两条木棒相交成的锐角的度数为10°,它们分别以与自身垂直的方向向两侧平移时,它们的交点A也随着移动(如图箭头所示),如果两条直线的移动速度都是光速的0.2倍,则交点A的移动速度是光速的 倍.(结果保留两个有效数字).
三.解答题(共8小题,满分66分)
19.在△ABC中,∠B、∠C 均为锐角,其对边分别为b、c,求证:=.
20.下列关系式是否成立(0<α<90°),请说明理由.
(1)sinα+cosα≤1;
(2)sin2α=2sinα.
21.计算:+()﹣1﹣4cos45°﹣()0.
22.如图,在△ABC中,∠A=30°,cosB=,AC=6.求AB的长.
23.一种拉杆式旅行箱的示意图如图所示,箱体长AB=50cm,拉杆最大伸长距离BC=35cm,(点A、B、C在同一条直线上),在箱体的底端装有一圆形滚轮⊙A,⊙A与水平地面切于点D,AE∥DN,某一时刻,拉杆拉到最长,点B距离水平面38cm,点C距离水平面59cm.
(1)求圆形滚轮的半径AD的长;
(2)当人的手自然下垂拉旅行箱时,人感觉较为舒服,已知某人的手自然下垂在点C处且拉杆达到最大延伸距离时,点C距离水平地面73.5cm,求此时拉杆箱与水平面AE所成角∠CAE的大小(精确到1°,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19).
24.已知:如图,斜坡AP的坡度为1:2.4,坡长AP为26米,在坡顶A处的同一水平面上有一座古塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角为76°.求:
(1)坡顶A到地面PQ的距离;
(2)古塔BC的高度(结果精确到1米).(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
25.重庆是一座美丽的山坡,某中学依山而建,校门A处,有一斜坡AB,长度为13米,在坡顶B处看教学楼CF的楼顶C的仰角∠CBF=53°,离B点4米远的E处有一花台,在E处仰望C的仰角∠CEF=63.4°,CF的延长线交校门处的水平面于D点,FD=5米.
(1)求斜坡AB的坡度i.
(2)求DC的长.(参考数据:tan53°≈,tan63.4°≈2)
26.如图,海中有一小岛P,在距小岛P的海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?
参考答案
一.选择题(共10小题,满分30分)
1.解:根据三角函数的定义:
A、sinA=,错误;
B、cosB=,错误;
C、tanA=,正确;
D、cotB=,错误.
故选:C.
2.解:∵sin30°=cos60°,
又16°<43°<60°,余弦值随着角度的增大而减小,
∴cos16°>cos43°>sin30°.
故选:C.
3.解:∵α为锐角,,
∴cos(90°﹣α)=sinα=.
故选:B.
4.解:∵Rt△ABC中,∠C=90°,sinA=,
∴cosA===,
∴∠A+∠B=90°,
∴sinB=cosA=.
故选:A.
5.解:∵cos30°=,
∴它的相反数为﹣.
故选:C.
6.解:由tan∠B=,得
AC=BC tanB=5×tan26°.
故选:D.
7.解:作AM⊥BC于M,DN⊥EF于N,如图,
在Rt△ABM中,∵sin∠B=,
∴AM=3sin50°,
∴S1=BC AM=×7×3sin50°=sin50°,
在Rt△DEN中,∠DEN=180°﹣130°=50°,
∵sin∠DEN=,
∴DN=7sin50°,
∴S2=EF DN=×3×7sin50°=sin50°,
∴S1=S2.
故选:D.
8.解:如图,过点A作BC的平行线AG,过点E作EH⊥AG于H,
则∠EHG=∠HEF=90°,
∵∠AEF=143°,
∴∠AEH=∠AEF﹣∠HEF=53°,
∠EAH=37°,
在△EAH中,∠EHA=90°,∠EAH=37°,AE=1.2米,
∴EH=AE sin∠EAH≈1.2×0.60=0.72(米),
∵AB=1.2米,
∴AB+EH≈1.2+0.72=1.92≈1.9米.
故选:A.
9.解:由于相邻两树之间的水平距离为5米,坡角为α,
则两树在坡面上的距离AB=.
故选:B.
10.解:根据俯角的定义,首先确定水平线,水平线以下与视线的夹角,即是俯角.
故选:C.
二.填空题(共8小题,满分24分)
11.解:连接AC,
由网格特点和正方形的性质可知,∠BAC=90°,
根据勾股定理得,AC=,AB=2,
则tan∠ABC==,
故答案为:.
12.解:∵cos44°=sin46°,正弦值随着角的增大而增大,
又∵44°<46°,
∴sin44°<cos44°.
故答案为:<.
13.解:分子分母同时除以cosx,原分式可化为:,
当tanx=2时,原式==.
故答案为:.
14.解:cot44° cot45° cot46°=cot44° cot46° cot45°=1 cot45°=1.
15.解:∵在△ABC中,|sinA﹣|+(cosB﹣)2=0,
∴sinA=,cosB=,
∴∠A=30°,∠B=60°,
∴∠C=180°﹣30°﹣60°=90°.
故答案为:90°.
16.解:(Ⅰ)sin60° cos30°﹣= ﹣=﹣=.
(Ⅱ)sin50°cos40°﹣≈0.0868>0.
故答案为:(Ⅰ).
(Ⅱ)>.
17.解:如图,过点A作AB⊥x轴,
则OB=2、AB=2,
∴OA===4,
∵cos∠AOB===,
∴∠AOB=60°,
作AO的中垂线交x轴于点P,交OA于点Q,
则OQ=AQ=2,
∴OP==4,
∵N(1,0),
∴PN=3,
∵MO=MA,
∴点M在PQ上,
当MN⊥PQ时,MN最小,
∵PQ⊥OA、PQ⊥MN,
∴MN=,
故答案为:.
18.解:如图,根据题意设光速为tm/s,
则一秒内,m与l移动的距离为0.2tm,
过A'作CA'⊥AC于A',
在Rt△ACA'中,∠A'AC1=10°÷2=5°,A'C=0.2tm,
∴AA'=CA'÷sin5°≈2.3,
∴A移动的距离约为2.3tm;
故交点A的移动速度是光速的2.3倍.
三.解答题(共8小题,满分66分)
19.证明:过A作AD⊥BC于D,
在Rt△ABD中,sinB=,
∴AD=ABsinB,
在Rt△ADC中,sinC=,
∴AD=ACsinC,
∴ABsinB=ACsinC,
而AB=c,AC=b,
∴csinB=bsinC,
∴=.
20.解:(1)该不等式不成立,理由如下:
如图,在△ABC中,∠B=90°,∠C=α.
则sinα+cosα=+=>1,故sinα+cosα≤1不成立;
(2)该等式不成立,理由如下:
假设α=30°,则sin2α=sin60°=,2sinα=2sin30°=2×=1,
∵≠1,
∴sin2α≠2sinα,即sin2α=2sinα不成立.
21.解:原式=2+2﹣4×﹣1,
=2+2﹣2﹣1,
=1.
故答案为:1.
22.解:过点C作CD⊥AB于点D.
∵∠A=30°,
∴CD=AC=3,AD=AC cosA=9,
∵cosB=,
∴设BD=4x,则BC=5x,
由勾股定理得,CD=3x,
由题意的,3x=3,
解得,x=,
∴BD=4,
∴AB=AD+BD=9+4.
23.解:(1)作BH⊥AF于点G,交DM于点H.
则BG∥CF
设圆形滚轮的半径AD的长是xcm.
则=,即=,
解得:x=8.
则圆形滚轮的半径AD的长是8cm;
(2)CF=73.5﹣8=65.5(Cm).
则sin∠CAF==≈0.77,
则∠CAF=50°.
24.解:(1)过点A作AH⊥PQ,垂足为点H.
∵斜坡AP的坡度为1:2.4,∴=,
设AH=5km,则PH=12km,
由勾股定理,得AP=13km.
∴13k=26. 解得k=2.
∴AH=10(m).
答:坡顶A到地面PQ的距离为10m.
(2)延长BC交PQ于点D.
∵BC⊥AC,AC∥PQ,
∴BD⊥PQ.
∴四边形AHDC是矩形,CD=AH=10,AC=DH.
∵∠BPD=45°,
∴PD=BD.
设BC=x,则x+10=24+DH.∴AC=DH=x﹣14.
在Rt△ABC中,tan76°=,即≈4.0,
解得x=,即x≈19,
答:古塔BC的高度约为19米.
25.解:(1)过B作BG⊥AD于G,
则四边形BGDF是矩形,
∴BG=DF=5米,
∵AB=13米,
∴AG==12米,
∴AB的坡度i==1:2.4;
(2)在Rt△BCF中,BF==,
在Rt△CEF中,EF==,
∵BE=4米,
∴BF﹣EF═﹣=4,
解得:CF=16.
∴DC=CF+DF=16+5=21米.
26.解:过P作PB⊥AM于B,
在Rt△APB中,∵∠PAB=30°,
∴PB=AP=×32=16海里,
∵16<16,
故轮船有触礁危险.
为了安全,应改变航行方向,并且保证点P到航线的距离不小于暗礁的半径16海里,即这个距离至少为16海里,
设安全航向为AC,作PD⊥AC于点D,
由题意得,AP=32海里,PD=16海里,
∵sin∠PAC===,
∴在Rt△PAD中,∠PAC=45°,
∴∠BAC=∠PAC﹣∠PAB=45°﹣30°=15°.
答:若轮船继续向正东方向航行,轮船有触礁危险.轮船自A处开始至少沿东偏南15°度方向航行,才能安全通过这一海域.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
