2021-2022学年青岛版九年级数学上册2.5解直角三角形的应用 解答专题训练(word版含答案)
文档属性
| 名称 | 2021-2022学年青岛版九年级数学上册2.5解直角三角形的应用 解答专题训练(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 424.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-15 22:44:33 | ||
图片预览




文档简介
2021-2022学年青岛版九年级数学上册《2.5解直角三角形的应用》解答专题训练(附答案)
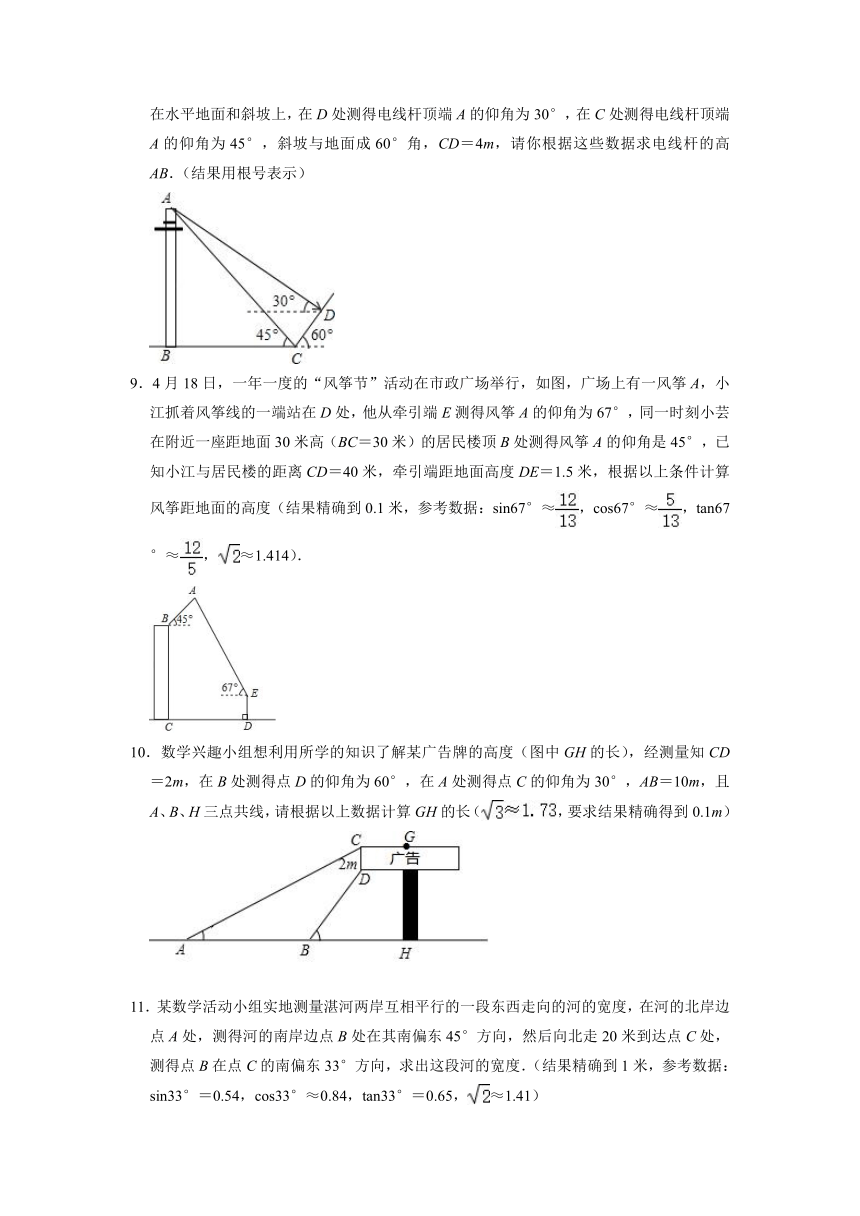
1.如图,河流的两岸PQ、MN互相平行,河岸PQ上有一排小树,已知相邻两树之间的距离CD=50米,某人在河岸MN的A处测的∠DAN=35°,然后沿河岸走了130米到达B处,测的∠CBN=60°,求河流的宽度CE(结果保留整数).
(参考数据:sin35°≈0.6,cos35°≈0.8,tan35°≈0.7,≈1.7)
2.海岛A的周围8 nmile 内有暗礁,渔船跟踪鱼群由西向东航行,在点B处测得海岛A位于北偏东67°,航行12nmlie到达C点,又测得小岛A在北偏东45°方向上.如果渔船不改变航线继续向东航行,那么它有没有触礁的危险?请说明理由.(参考数据:sin67°≈,cos67°,tan67°≈)
3.如图,某教学楼AB的后面有一建筑物CD,当光线与地面夹角是22°时,教学楼在建筑物的墙上留下高2米的影子CE;而当光线与地面夹角是45°时,教学楼顶A在地面上的影子F与墙角C有13米的距离(B、F、C在一条直线上),求教学楼AB的高度(sin22°≈,cos22°≈,tan22°≈)
4.某中学紧挨一座山坡,如图所示,已知AF∥BC,AB长30米,∠ABC=66°,为防止山体滑坡,需要改造山坡,改造后的山坡BE与地面成45°角,求AE是多少米?(精确到1米)
(参考数据:sin66°≈0.91,cos66°≈0.41,tan66°≈2.25)
5.如图,AC时一棵大树,BF是一个斜坡,坡角为30°,某时刻太阳光直射斜坡BF,树顶端A的影子落到斜坡上的点D处,已知BC=6m,BD=4m,求树高AC的高度(结果精确到0.1m,参考数据:≈1.414,≈1.732)
6.某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援,伤员在C处,直升机在A处,伤员离云梯(AP)150米(即CP的长).伤员从C地前往云梯的同时,直升机受到惯性的影响又往前水平行进50米到达B处,此时云梯也移动到BQ位置,已知∠ACP=30°,∠APQ=60°,∠BQI=43°.问:伤员需前行多少米才能够到云梯?(结果保留整数,sin43°=0.68,cos43°=0.73,tan43°=0.93,≈1.73)
7.数学小组的两位同学准备测量两幢教学楼之间的距离,如图,两幢教学楼AB和CD之间有一景观池(AB⊥BD,CD⊥BD),一同学在A点测得池中喷泉处E点的俯角为42°,另一同学在C点测得E点的俯角为45°(点B,E,D在同一直线上),两个同学已经在学校资料室查出楼高AB=15m,CD=20m,求两幢教学楼之间的距离BD.
(结果精确到0.1m,参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
8.某校王老师组织九(1)班同学开展数学活动,某天带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D处测得电线杆顶端A的仰角为30°,在C处测得电线杆顶端A的仰角为45°,斜坡与地面成60°角,CD=4m,请你根据这些数据求电线杆的高AB.(结果用根号表示)
9.4月18日,一年一度的“风筝节”活动在市政广场举行,如图,广场上有一风筝A,小江抓着风筝线的一端站在D处,他从牵引端E测得风筝A的仰角为67°,同一时刻小芸在附近一座距地面30米高(BC=30米)的居民楼顶B处测得风筝A的仰角是45°,已知小江与居民楼的距离CD=40米,牵引端距地面高度DE=1.5米,根据以上条件计算风筝距地面的高度(结果精确到0.1米,参考数据:sin67°≈,cos67°≈,tan67°≈,≈1.414).
10.数学兴趣小组想利用所学的知识了解某广告牌的高度(图中GH的长),经测量知CD=2m,在B处测得点D的仰角为60°,在A处测得点C的仰角为30°,AB=10m,且A、B、H三点共线,请根据以上数据计算GH的长(,要求结果精确得到0.1m)
11.某数学活动小组实地测量湛河两岸互相平行的一段东西走向的河的宽度,在河的北岸边点A处,测得河的南岸边点B处在其南偏东45°方向,然后向北走20米到达点C处,测得点B在点C的南偏东33°方向,求出这段河的宽度.(结果精确到1米,参考数据:sin33°=0.54,cos33°≈0.84,tan33°=0.65,≈1.41)
12.如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需要绕行B地,已知B位于A地北偏东67°方向,距离A地520km,C地位于B地南偏东30°方向,若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长(结果保留整数)
参考数据:(sin67°≈;cos67°≈;tan67°≈;≈1.73)
13.钓鱼岛自古就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视巡航.一日,中国一艘海监船从A点沿正北方向巡航,其航线距钓鱼岛(设N、M为该岛的东西两端点)最近距离为15海里(即MC=15海里),在A点测得岛屿的西端点M在点A的东北方向,航行4海里后到达B点,测得岛屿的东端点N在点B的北偏东57°方向(其中N、M、C在同一条直线上),求钓鱼岛东西两端点MN之间的距离.(精确到0.1海里,参考数据:sin57°≈0.84,cos57°=0.54,tan57°≈1.54.)
14.钓鱼岛自古就是中国的!2017年5月18日,中国海警2305,2308,2166,33115舰船队在中国的钓鱼岛领海内巡航,如图,我军以30km/h的速度在钓鱼岛A附近进行合法巡逻,当巡逻舰行驶到B处时,战士发现A在他的东北方向,巡逻舰继续向北航行40分钟后到达点C,发现A在他的东偏北15°方向,求此时巡逻舰与钓鱼岛的距离(≈1.414,结果精确到0.01)
15.如图所示,小明在自家楼顶上的点A处测量建在与小明家楼房同一水平线上邻居的电梯楼的高度,测得电梯楼顶部B处的仰角为60°,底部C处的俯角为26°,已知小明家楼房的高度AD=15米,求电梯楼的高度BC.(结果精确到0.1米,参考数据:≈1.73,sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)
16.向阳中学校园内有一条林萌道叫“勤学路”,道路两边有如图所示的路灯(在铅垂面内的示意图),灯柱BC的高为10米,灯柱BC与灯杆AB的夹角为120°.路灯采用锥形灯罩,在地面上的照射区域DE的长为13.3米,从D、E两处测得路灯A的仰角分别为α和45°,且tanα=6.求灯杆AB的长度.
17.在小水池旁有一盏路灯,已知支架AB的长是0.8m,A端到地面的距离AC是4m,支架AB与灯柱AC的夹角为65°.小明在水池的外沿D测得支架B端的仰角是45°,在水池的内沿E测得支架A端的仰角是50°(点C、E、D在同一直线上),求小水池的宽DE.(结果精确到0.1m)(sin65°≈0.9,cos65°≈0.4,tan50°≈1.2)
18.如图,在大楼AB正前方有一斜坡CD,坡角∠DCE=30°,楼高AB=60米,在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的D处测得楼顶B的仰角为45°,其中点A,C,E在同一直线上.
(1)求坡底C点到大楼距离AC的值;
(2)求斜坡CD的长度.
19.如图,甲、乙两座建筑物的水平距离BC为78m,从甲的顶部A处测得乙的顶部D处的俯角为48°,测得底部C处的俯角为58°,求甲、乙建筑物的高度AB和DC(结果取整数).参考数据:tan48°≈1.11,tan58°≈1.60.
20.如图1,被誉为“中原第一高楼”的郑州会展宾馆(俗称“玉米楼”)就坐落在风景如画的如意湖畔,也是来郑观光的游客留影的最佳景点.学完了三角函数后,刘明和王华决定用自己学到的知识测量“玉米楼”的高度.如图2,刘明在点C处测得楼顶B的仰角为45°,王华在高台上测得楼顶的仰角为30°.若高台高DE为5米,点D到点C的水平距离EC为187.5米,A、C、E三点共线,求“玉米楼”AB的高(,结果保留整数).
21.实验小组的学生小溪想测量一处路灯杆的高度如图,她在楼上距地面6米高的窗口C处,测得正前方路灯杆顶部A点的仰角为37°,路灯杆底部B点的俯角为45°,另外,路灯杆下面水泥台的高度为0.84米,则路灯杆AB的高度为多少米?(结果保留整数.参考数据:sin37°≈0.60,cos37°≈0.80.tan37°≈0.75)
参考答案
1.解:过点C作CF∥DA交AB于点F.
∵MN∥PQ,CF∥DA,
∴四边形AFCD是平行四边形.
∴AF=CD=50m,∠CFB=35°.
∴FB=AB﹣AF=130﹣50=80(m),
设BE=x,∵∠CBN=60°,
∴EC=x,
∴tan35°=≈0.7,
即=0.7,
解得:x=56,
∴CE=56×1.7≈95.2≈95(m),
答:河流的宽是95米.
2.解:作AD⊥BC,交BC的延长线于D,
设AD为xnmile,
由题意得,∠B=90°﹣67°=23°,∠ACD=90°﹣45°=45°,
则CD=AD tan45°=x,BD=,
BD﹣CD=BC,
由题意得,,
解得x=,
∵8nmile<nmile,
∴渔船没有触礁的危险.
3.解:过点E作EM⊥AB,垂足为M.
设AB为x.
Rt△ABF中,∠AFB=45°,
∴BF=AB=x,
∴BC=BF+FC=x+13,
在Rt△AEM中,∠AEM=22°,AM=AB﹣BM=AB﹣CE=x﹣2,
tan22°=,
则=,
解得:x=12.
即教学楼的高为12m.
4.解:在Rt△ADB中,AB=30米∠ABC=60°
AD=AB sin∠ABC=30×sin66°=30×0.91=27.3(米),
DB=AB cos∠ABC=30×cos66°=30×0.41=12.3(米).
连接BE,过E作EN⊥BC于N,如图所示:
∵AE∥BC,
∴四边形AEND是矩形NE=AD≈27.3米,
在Rt△ENB中,∠EBN=45°时,BN=EN=AD=27.3米,
∴AE=DN=BN﹣BD=27.3﹣12.3=15米
答:AE是15米.
5.解:如图,过点D作DP⊥BE于点P,作DQ⊥AC于点Q,
∵∠DBP=30°、BD=4,
∴CQ=DP=BD=2,BP=BDcos∠DBP=4×=2,
则DQ=CP=BP+BC=2+6,
∵太阳光直射斜坡BF,
∴∠ADP=90°,
又∵∠QDB=∠DBP=30°,
∴∠ADQ=60°,
则AQ=DQtan∠ADQ=(2+6)=6+6,
∴树高AC=AQ+CQ=6+6+2=8+6≈18.4(m),
答:树高AC的高度约为18.4m.
6.解:作AE⊥CP,BF⊥CP分别于点E、F.
∵∠APQ=∠C+∠CAP,
∴∠CAP=∠APQ﹣∠ACP=60°﹣30°=30°,
∴∠ACP=∠CAP,
∴AP=CP=150(米),
在直角△APE中,AE=AP sin∠APE=150×=75(米),
PE=AP cos∠APE=150×cos60°=75(米).
∵在直角△BQF中,BF=AE=75米.
tan∠BQF=,
∴QF==.
∴则CQ=CP+PQ=CP+PE+EF﹣QF=150+75+50﹣=150+125﹣≈275﹣≈275﹣139.5≈136(米).
答:伤员需前行136米才能够到云梯.
7.解:由题意可得:∠AEB=42°,∠CED=45°,
故tan42°==≈0.90,
解得:AB≈16.67(m),
tan45°==1,
故DC=ED=20m,
故BD=16.67+20≈36.7(m),
答:两幢教学楼之间的距离BD为36.7m.
8.解:延长AD交BC的延长线于G,作DH⊥BG于H,
在Rt△DHC中,∠DCH=60°,CD=4,
则CH=CD cos∠DCH=4×cos60°=2,
DH=CD sin∠DCH=4×sin60°=,
∵DH⊥BG,∠G=30°,
∴HG===6,
∴CG=CH+HG=2+6=8,
设AB=xm,
∵AB⊥BG,∠G=30°,∠BCA=45°,
∴BC=x,BG==x,
∵BG﹣BC=CG,
∴x﹣x=8,
解得:x==4(+1)(m)
答:电线杆的高为x=4(+1)m.
9.解:如图,作AM⊥CD于M,作BF⊥AM于F,EH⊥AM于H.
∵∠ABF=45°,∠AFB=90°,
∴AF=BF,设AF=BF=x,则CM=BF=x,DM=HE=40﹣x,AH=x+30﹣1.5=x+28.5,
在Rt△AHE中,tan67°=,
∴=,
解得x=19.9m.
∴AM=19.9+30=49.9m.
∴风筝距地面的高度49.9m.
10.解:如图,过点D作DE⊥AH于点E,设DE=xm,则CE=(x+2)m.
在Rt△AEC和Rt△BED中,有tan30°=,
tan60°=,
∴AE=(x+2),BE=x,
∵AE﹣BE=AB=10,
∴(x+2)﹣x=10,
∴x=5﹣3,
∴GH=CD+DE=2+5﹣3=5﹣1≈7.7(m).
答:GH的长约为7.7m.
11.解:如图,延长CA交BE于点D,
则CD⊥BE,
由题意知,∠DAB=45°,∠DCB=33°,
设AD=x米,
则BD=x米,CD=(20+x)米,
在Rt△CDB中,=tan∠DCB,
∴=tan33°≈0.65,
解得x≈37,
答:这段河的宽约为37米.
12.解:过点B作BD⊥AC于点D,
∵B地位于A地北偏东67°方向,距离A地520km,
∴∠ABD=67°,
∴AD=AB sin67°≈520×=480km,
BD=AB cos67°≈520×=200km.
∵C地位于B地南偏东30°方向,
∴∠CBD=30°,
∴CD=BD tan30°=200×≈113.9km,
∴AC=AD+CD=480+113.9≈594(km).
答:A地到C地之间高铁线路的长为594km.
13.解:在Rt△ACM中,tan∠CAM=tan45°==1,
∴AC=CM=15,
∴BC=AC﹣AB=15﹣4=11.
在Rt△BCN中,tan∠CBN=tan57°==1.54.
∴CN=1.54B C=16.94.
∴MN=16.94﹣15=1.94≈1.9海里.
答:钓鱼岛东西两端点MN之间的距离约为1.9海里.
14.解:作CD⊥AB于D,
由题意得∠B=45°,∠ACB=105°,
∴∠A=30°,
40分钟=小时,
BC=30×=20km,
在Rt△BCD中,sinB==,
∴CD=10km
在Rt△ACD中,sinA==,
∴AC=20≈28.28km.
故此时巡逻舰与钓鱼岛的距离是28.28km.
15.解:过点A作AE⊥BC于E,
∵AD⊥CD,BC⊥CD,
∴四边形ADCE是矩形,
∴CE=AD=15米,
在Rt△ACE中,AE==≈30.6(米),
在Rt△ABE中,BE=AE tan60°=52.9(米),
∴BC=CE+BE=15+52.9=67.9(米).
答:电梯楼的高度BC为67.9米.
16.解:过点A作AF⊥CE,交CE于点F,过点B作BG⊥AF,交AF于点G,则FG=BC=10.
由题意得∠ADE=α,∠E=45°.
设AF=x.
∵∠E=45°,
∴EF=AF=x.
在Rt△ADF中,∵tan∠ADF=,
∴DF==,
∵DE=13.3,
∴x+=13.3.
∴x=11.4.
∴AG=AF﹣GF=11.4﹣10=1.4.
∵∠ABC=120°,
∴∠ABG=∠ABC﹣∠CBG=120°﹣90°=30°.
∴AB=2AG=2.8,
答:灯杆AB的长度为2.8米.
17.解:过点B作BF⊥AC于F,BG⊥CD于G,
在Rt△BAF中,∠BAF=65°,BF=AB sin∠BAF=0.8×0.9=0.72(m),
AF=AB cos∠BAF=0.8×0.4=0.32(m),
∴FC=AF+AC=4.32(m),
∵四边形FCGB是矩形,
∴BG=FC=4.32(m),CG=BF=0.72(m),
∵∠BDG=45°,
∴∠BDG=∠GBD,
∴GD=GB=4.32(m),
∴CD=CG+GD=5.04(m),
在Rt△ACE中,∠AEC=50°,CE=(m),
∴DE=CD﹣CE=5.04﹣3.33=1.71≈1.7(m),
答:小水池的宽DE为1.7m.
18.解:(1)在直角△ABC中,∠BAC=90°,∠BCA=60°,AB=60米,则AC===20(米)
答:坡底C点到大楼距离AC的值是20米.
(2)设CD=2x,则DE=x,CE=x,
在Rt△BDF中,∵∠BDF=45°,
∴BF=DF,
∴60﹣x=20+x,
∴x=40﹣60,
∴CD=2x=(80﹣120)(米),
∴CD的长为(80﹣120)米.
19.解:如图作AE⊥CD交CD的延长线于E.则四边形ABCE是矩形,
∴AE=BC=78(m),AB=CE,
在Rt△ACE中,EC=AE tan58°≈125(m)
在Rt△AED中,DE=AE tan48°,
∴CD=EC﹣DE=AE tan58°﹣AE tan48°=78×1.6﹣78×1.11≈38(m),
答:甲、乙建筑物的高度AB约为125m,DC约为38m.
20.解:作DM⊥AB于M,交BC于F,作CG⊥DM于G,
设BM=x米,
由题意得,DG=187.5米,CG=5米,∠BFM=45°,∠BDM=30°,
则GF=CG=5米,DF=DG+GF=192.5米,FM=BM=x米,
∴DM==x,
∵DM﹣FM=DF,
∴x﹣x=192.5,
解得,x=≈2760,
260+5=265(米).
答:“玉米楼”AB的高约为265米.
21.解:作CE⊥AB于E.
在Rt△BCE中,BE=6﹣0.84=5.16m,
∵∠ECB=∠EBC=45°,
∴EC=EB=5.16(m),
在Rt△ACE中,AE=EC tan37°=6.16×0.75≈3.87(m),
∴AB=AE+EB=3.87+5.16=9.03≈9(m),
答:路灯杆AB的高度为9m.
1.如图,河流的两岸PQ、MN互相平行,河岸PQ上有一排小树,已知相邻两树之间的距离CD=50米,某人在河岸MN的A处测的∠DAN=35°,然后沿河岸走了130米到达B处,测的∠CBN=60°,求河流的宽度CE(结果保留整数).
(参考数据:sin35°≈0.6,cos35°≈0.8,tan35°≈0.7,≈1.7)
2.海岛A的周围8 nmile 内有暗礁,渔船跟踪鱼群由西向东航行,在点B处测得海岛A位于北偏东67°,航行12nmlie到达C点,又测得小岛A在北偏东45°方向上.如果渔船不改变航线继续向东航行,那么它有没有触礁的危险?请说明理由.(参考数据:sin67°≈,cos67°,tan67°≈)
3.如图,某教学楼AB的后面有一建筑物CD,当光线与地面夹角是22°时,教学楼在建筑物的墙上留下高2米的影子CE;而当光线与地面夹角是45°时,教学楼顶A在地面上的影子F与墙角C有13米的距离(B、F、C在一条直线上),求教学楼AB的高度(sin22°≈,cos22°≈,tan22°≈)
4.某中学紧挨一座山坡,如图所示,已知AF∥BC,AB长30米,∠ABC=66°,为防止山体滑坡,需要改造山坡,改造后的山坡BE与地面成45°角,求AE是多少米?(精确到1米)
(参考数据:sin66°≈0.91,cos66°≈0.41,tan66°≈2.25)
5.如图,AC时一棵大树,BF是一个斜坡,坡角为30°,某时刻太阳光直射斜坡BF,树顶端A的影子落到斜坡上的点D处,已知BC=6m,BD=4m,求树高AC的高度(结果精确到0.1m,参考数据:≈1.414,≈1.732)
6.某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援,伤员在C处,直升机在A处,伤员离云梯(AP)150米(即CP的长).伤员从C地前往云梯的同时,直升机受到惯性的影响又往前水平行进50米到达B处,此时云梯也移动到BQ位置,已知∠ACP=30°,∠APQ=60°,∠BQI=43°.问:伤员需前行多少米才能够到云梯?(结果保留整数,sin43°=0.68,cos43°=0.73,tan43°=0.93,≈1.73)
7.数学小组的两位同学准备测量两幢教学楼之间的距离,如图,两幢教学楼AB和CD之间有一景观池(AB⊥BD,CD⊥BD),一同学在A点测得池中喷泉处E点的俯角为42°,另一同学在C点测得E点的俯角为45°(点B,E,D在同一直线上),两个同学已经在学校资料室查出楼高AB=15m,CD=20m,求两幢教学楼之间的距离BD.
(结果精确到0.1m,参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
8.某校王老师组织九(1)班同学开展数学活动,某天带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D处测得电线杆顶端A的仰角为30°,在C处测得电线杆顶端A的仰角为45°,斜坡与地面成60°角,CD=4m,请你根据这些数据求电线杆的高AB.(结果用根号表示)
9.4月18日,一年一度的“风筝节”活动在市政广场举行,如图,广场上有一风筝A,小江抓着风筝线的一端站在D处,他从牵引端E测得风筝A的仰角为67°,同一时刻小芸在附近一座距地面30米高(BC=30米)的居民楼顶B处测得风筝A的仰角是45°,已知小江与居民楼的距离CD=40米,牵引端距地面高度DE=1.5米,根据以上条件计算风筝距地面的高度(结果精确到0.1米,参考数据:sin67°≈,cos67°≈,tan67°≈,≈1.414).
10.数学兴趣小组想利用所学的知识了解某广告牌的高度(图中GH的长),经测量知CD=2m,在B处测得点D的仰角为60°,在A处测得点C的仰角为30°,AB=10m,且A、B、H三点共线,请根据以上数据计算GH的长(,要求结果精确得到0.1m)
11.某数学活动小组实地测量湛河两岸互相平行的一段东西走向的河的宽度,在河的北岸边点A处,测得河的南岸边点B处在其南偏东45°方向,然后向北走20米到达点C处,测得点B在点C的南偏东33°方向,求出这段河的宽度.(结果精确到1米,参考数据:sin33°=0.54,cos33°≈0.84,tan33°=0.65,≈1.41)
12.如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需要绕行B地,已知B位于A地北偏东67°方向,距离A地520km,C地位于B地南偏东30°方向,若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长(结果保留整数)
参考数据:(sin67°≈;cos67°≈;tan67°≈;≈1.73)
13.钓鱼岛自古就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视巡航.一日,中国一艘海监船从A点沿正北方向巡航,其航线距钓鱼岛(设N、M为该岛的东西两端点)最近距离为15海里(即MC=15海里),在A点测得岛屿的西端点M在点A的东北方向,航行4海里后到达B点,测得岛屿的东端点N在点B的北偏东57°方向(其中N、M、C在同一条直线上),求钓鱼岛东西两端点MN之间的距离.(精确到0.1海里,参考数据:sin57°≈0.84,cos57°=0.54,tan57°≈1.54.)
14.钓鱼岛自古就是中国的!2017年5月18日,中国海警2305,2308,2166,33115舰船队在中国的钓鱼岛领海内巡航,如图,我军以30km/h的速度在钓鱼岛A附近进行合法巡逻,当巡逻舰行驶到B处时,战士发现A在他的东北方向,巡逻舰继续向北航行40分钟后到达点C,发现A在他的东偏北15°方向,求此时巡逻舰与钓鱼岛的距离(≈1.414,结果精确到0.01)
15.如图所示,小明在自家楼顶上的点A处测量建在与小明家楼房同一水平线上邻居的电梯楼的高度,测得电梯楼顶部B处的仰角为60°,底部C处的俯角为26°,已知小明家楼房的高度AD=15米,求电梯楼的高度BC.(结果精确到0.1米,参考数据:≈1.73,sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)
16.向阳中学校园内有一条林萌道叫“勤学路”,道路两边有如图所示的路灯(在铅垂面内的示意图),灯柱BC的高为10米,灯柱BC与灯杆AB的夹角为120°.路灯采用锥形灯罩,在地面上的照射区域DE的长为13.3米,从D、E两处测得路灯A的仰角分别为α和45°,且tanα=6.求灯杆AB的长度.
17.在小水池旁有一盏路灯,已知支架AB的长是0.8m,A端到地面的距离AC是4m,支架AB与灯柱AC的夹角为65°.小明在水池的外沿D测得支架B端的仰角是45°,在水池的内沿E测得支架A端的仰角是50°(点C、E、D在同一直线上),求小水池的宽DE.(结果精确到0.1m)(sin65°≈0.9,cos65°≈0.4,tan50°≈1.2)
18.如图,在大楼AB正前方有一斜坡CD,坡角∠DCE=30°,楼高AB=60米,在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的D处测得楼顶B的仰角为45°,其中点A,C,E在同一直线上.
(1)求坡底C点到大楼距离AC的值;
(2)求斜坡CD的长度.
19.如图,甲、乙两座建筑物的水平距离BC为78m,从甲的顶部A处测得乙的顶部D处的俯角为48°,测得底部C处的俯角为58°,求甲、乙建筑物的高度AB和DC(结果取整数).参考数据:tan48°≈1.11,tan58°≈1.60.
20.如图1,被誉为“中原第一高楼”的郑州会展宾馆(俗称“玉米楼”)就坐落在风景如画的如意湖畔,也是来郑观光的游客留影的最佳景点.学完了三角函数后,刘明和王华决定用自己学到的知识测量“玉米楼”的高度.如图2,刘明在点C处测得楼顶B的仰角为45°,王华在高台上测得楼顶的仰角为30°.若高台高DE为5米,点D到点C的水平距离EC为187.5米,A、C、E三点共线,求“玉米楼”AB的高(,结果保留整数).
21.实验小组的学生小溪想测量一处路灯杆的高度如图,她在楼上距地面6米高的窗口C处,测得正前方路灯杆顶部A点的仰角为37°,路灯杆底部B点的俯角为45°,另外,路灯杆下面水泥台的高度为0.84米,则路灯杆AB的高度为多少米?(结果保留整数.参考数据:sin37°≈0.60,cos37°≈0.80.tan37°≈0.75)
参考答案
1.解:过点C作CF∥DA交AB于点F.
∵MN∥PQ,CF∥DA,
∴四边形AFCD是平行四边形.
∴AF=CD=50m,∠CFB=35°.
∴FB=AB﹣AF=130﹣50=80(m),
设BE=x,∵∠CBN=60°,
∴EC=x,
∴tan35°=≈0.7,
即=0.7,
解得:x=56,
∴CE=56×1.7≈95.2≈95(m),
答:河流的宽是95米.
2.解:作AD⊥BC,交BC的延长线于D,
设AD为xnmile,
由题意得,∠B=90°﹣67°=23°,∠ACD=90°﹣45°=45°,
则CD=AD tan45°=x,BD=,
BD﹣CD=BC,
由题意得,,
解得x=,
∵8nmile<nmile,
∴渔船没有触礁的危险.
3.解:过点E作EM⊥AB,垂足为M.
设AB为x.
Rt△ABF中,∠AFB=45°,
∴BF=AB=x,
∴BC=BF+FC=x+13,
在Rt△AEM中,∠AEM=22°,AM=AB﹣BM=AB﹣CE=x﹣2,
tan22°=,
则=,
解得:x=12.
即教学楼的高为12m.
4.解:在Rt△ADB中,AB=30米∠ABC=60°
AD=AB sin∠ABC=30×sin66°=30×0.91=27.3(米),
DB=AB cos∠ABC=30×cos66°=30×0.41=12.3(米).
连接BE,过E作EN⊥BC于N,如图所示:
∵AE∥BC,
∴四边形AEND是矩形NE=AD≈27.3米,
在Rt△ENB中,∠EBN=45°时,BN=EN=AD=27.3米,
∴AE=DN=BN﹣BD=27.3﹣12.3=15米
答:AE是15米.
5.解:如图,过点D作DP⊥BE于点P,作DQ⊥AC于点Q,
∵∠DBP=30°、BD=4,
∴CQ=DP=BD=2,BP=BDcos∠DBP=4×=2,
则DQ=CP=BP+BC=2+6,
∵太阳光直射斜坡BF,
∴∠ADP=90°,
又∵∠QDB=∠DBP=30°,
∴∠ADQ=60°,
则AQ=DQtan∠ADQ=(2+6)=6+6,
∴树高AC=AQ+CQ=6+6+2=8+6≈18.4(m),
答:树高AC的高度约为18.4m.
6.解:作AE⊥CP,BF⊥CP分别于点E、F.
∵∠APQ=∠C+∠CAP,
∴∠CAP=∠APQ﹣∠ACP=60°﹣30°=30°,
∴∠ACP=∠CAP,
∴AP=CP=150(米),
在直角△APE中,AE=AP sin∠APE=150×=75(米),
PE=AP cos∠APE=150×cos60°=75(米).
∵在直角△BQF中,BF=AE=75米.
tan∠BQF=,
∴QF==.
∴则CQ=CP+PQ=CP+PE+EF﹣QF=150+75+50﹣=150+125﹣≈275﹣≈275﹣139.5≈136(米).
答:伤员需前行136米才能够到云梯.
7.解:由题意可得:∠AEB=42°,∠CED=45°,
故tan42°==≈0.90,
解得:AB≈16.67(m),
tan45°==1,
故DC=ED=20m,
故BD=16.67+20≈36.7(m),
答:两幢教学楼之间的距离BD为36.7m.
8.解:延长AD交BC的延长线于G,作DH⊥BG于H,
在Rt△DHC中,∠DCH=60°,CD=4,
则CH=CD cos∠DCH=4×cos60°=2,
DH=CD sin∠DCH=4×sin60°=,
∵DH⊥BG,∠G=30°,
∴HG===6,
∴CG=CH+HG=2+6=8,
设AB=xm,
∵AB⊥BG,∠G=30°,∠BCA=45°,
∴BC=x,BG==x,
∵BG﹣BC=CG,
∴x﹣x=8,
解得:x==4(+1)(m)
答:电线杆的高为x=4(+1)m.
9.解:如图,作AM⊥CD于M,作BF⊥AM于F,EH⊥AM于H.
∵∠ABF=45°,∠AFB=90°,
∴AF=BF,设AF=BF=x,则CM=BF=x,DM=HE=40﹣x,AH=x+30﹣1.5=x+28.5,
在Rt△AHE中,tan67°=,
∴=,
解得x=19.9m.
∴AM=19.9+30=49.9m.
∴风筝距地面的高度49.9m.
10.解:如图,过点D作DE⊥AH于点E,设DE=xm,则CE=(x+2)m.
在Rt△AEC和Rt△BED中,有tan30°=,
tan60°=,
∴AE=(x+2),BE=x,
∵AE﹣BE=AB=10,
∴(x+2)﹣x=10,
∴x=5﹣3,
∴GH=CD+DE=2+5﹣3=5﹣1≈7.7(m).
答:GH的长约为7.7m.
11.解:如图,延长CA交BE于点D,
则CD⊥BE,
由题意知,∠DAB=45°,∠DCB=33°,
设AD=x米,
则BD=x米,CD=(20+x)米,
在Rt△CDB中,=tan∠DCB,
∴=tan33°≈0.65,
解得x≈37,
答:这段河的宽约为37米.
12.解:过点B作BD⊥AC于点D,
∵B地位于A地北偏东67°方向,距离A地520km,
∴∠ABD=67°,
∴AD=AB sin67°≈520×=480km,
BD=AB cos67°≈520×=200km.
∵C地位于B地南偏东30°方向,
∴∠CBD=30°,
∴CD=BD tan30°=200×≈113.9km,
∴AC=AD+CD=480+113.9≈594(km).
答:A地到C地之间高铁线路的长为594km.
13.解:在Rt△ACM中,tan∠CAM=tan45°==1,
∴AC=CM=15,
∴BC=AC﹣AB=15﹣4=11.
在Rt△BCN中,tan∠CBN=tan57°==1.54.
∴CN=1.54B C=16.94.
∴MN=16.94﹣15=1.94≈1.9海里.
答:钓鱼岛东西两端点MN之间的距离约为1.9海里.
14.解:作CD⊥AB于D,
由题意得∠B=45°,∠ACB=105°,
∴∠A=30°,
40分钟=小时,
BC=30×=20km,
在Rt△BCD中,sinB==,
∴CD=10km
在Rt△ACD中,sinA==,
∴AC=20≈28.28km.
故此时巡逻舰与钓鱼岛的距离是28.28km.
15.解:过点A作AE⊥BC于E,
∵AD⊥CD,BC⊥CD,
∴四边形ADCE是矩形,
∴CE=AD=15米,
在Rt△ACE中,AE==≈30.6(米),
在Rt△ABE中,BE=AE tan60°=52.9(米),
∴BC=CE+BE=15+52.9=67.9(米).
答:电梯楼的高度BC为67.9米.
16.解:过点A作AF⊥CE,交CE于点F,过点B作BG⊥AF,交AF于点G,则FG=BC=10.
由题意得∠ADE=α,∠E=45°.
设AF=x.
∵∠E=45°,
∴EF=AF=x.
在Rt△ADF中,∵tan∠ADF=,
∴DF==,
∵DE=13.3,
∴x+=13.3.
∴x=11.4.
∴AG=AF﹣GF=11.4﹣10=1.4.
∵∠ABC=120°,
∴∠ABG=∠ABC﹣∠CBG=120°﹣90°=30°.
∴AB=2AG=2.8,
答:灯杆AB的长度为2.8米.
17.解:过点B作BF⊥AC于F,BG⊥CD于G,
在Rt△BAF中,∠BAF=65°,BF=AB sin∠BAF=0.8×0.9=0.72(m),
AF=AB cos∠BAF=0.8×0.4=0.32(m),
∴FC=AF+AC=4.32(m),
∵四边形FCGB是矩形,
∴BG=FC=4.32(m),CG=BF=0.72(m),
∵∠BDG=45°,
∴∠BDG=∠GBD,
∴GD=GB=4.32(m),
∴CD=CG+GD=5.04(m),
在Rt△ACE中,∠AEC=50°,CE=(m),
∴DE=CD﹣CE=5.04﹣3.33=1.71≈1.7(m),
答:小水池的宽DE为1.7m.
18.解:(1)在直角△ABC中,∠BAC=90°,∠BCA=60°,AB=60米,则AC===20(米)
答:坡底C点到大楼距离AC的值是20米.
(2)设CD=2x,则DE=x,CE=x,
在Rt△BDF中,∵∠BDF=45°,
∴BF=DF,
∴60﹣x=20+x,
∴x=40﹣60,
∴CD=2x=(80﹣120)(米),
∴CD的长为(80﹣120)米.
19.解:如图作AE⊥CD交CD的延长线于E.则四边形ABCE是矩形,
∴AE=BC=78(m),AB=CE,
在Rt△ACE中,EC=AE tan58°≈125(m)
在Rt△AED中,DE=AE tan48°,
∴CD=EC﹣DE=AE tan58°﹣AE tan48°=78×1.6﹣78×1.11≈38(m),
答:甲、乙建筑物的高度AB约为125m,DC约为38m.
20.解:作DM⊥AB于M,交BC于F,作CG⊥DM于G,
设BM=x米,
由题意得,DG=187.5米,CG=5米,∠BFM=45°,∠BDM=30°,
则GF=CG=5米,DF=DG+GF=192.5米,FM=BM=x米,
∴DM==x,
∵DM﹣FM=DF,
∴x﹣x=192.5,
解得,x=≈2760,
260+5=265(米).
答:“玉米楼”AB的高约为265米.
21.解:作CE⊥AB于E.
在Rt△BCE中,BE=6﹣0.84=5.16m,
∵∠ECB=∠EBC=45°,
∴EC=EB=5.16(m),
在Rt△ACE中,AE=EC tan37°=6.16×0.75≈3.87(m),
∴AB=AE+EB=3.87+5.16=9.03≈9(m),
答:路灯杆AB的高度为9m.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
