4.4.3 不同函数增长的差异(教案)-高中数学人教A版(2019)必修第一册
文档属性
| 名称 | 4.4.3 不同函数增长的差异(教案)-高中数学人教A版(2019)必修第一册 |  | |
| 格式 | doc | ||
| 文件大小 | 208.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-15 10:16:24 | ||
图片预览

文档简介
第四章 指数函数与对数函数
4.4.3 不同函数增长的差异
教学设计
一、教学目标
1.结合具体函数图像,总结一次函数、指数函数、对数函数的增长差异.
2.通过图像,了解“直线上升”“对数增长”“指数爆炸”的含义.
二、教学重难点
1.教学重点
研究一次函数、指数函数、对数函数的增长差异.
2.教学难点
函数增长快慢的因素.
三、教学过程
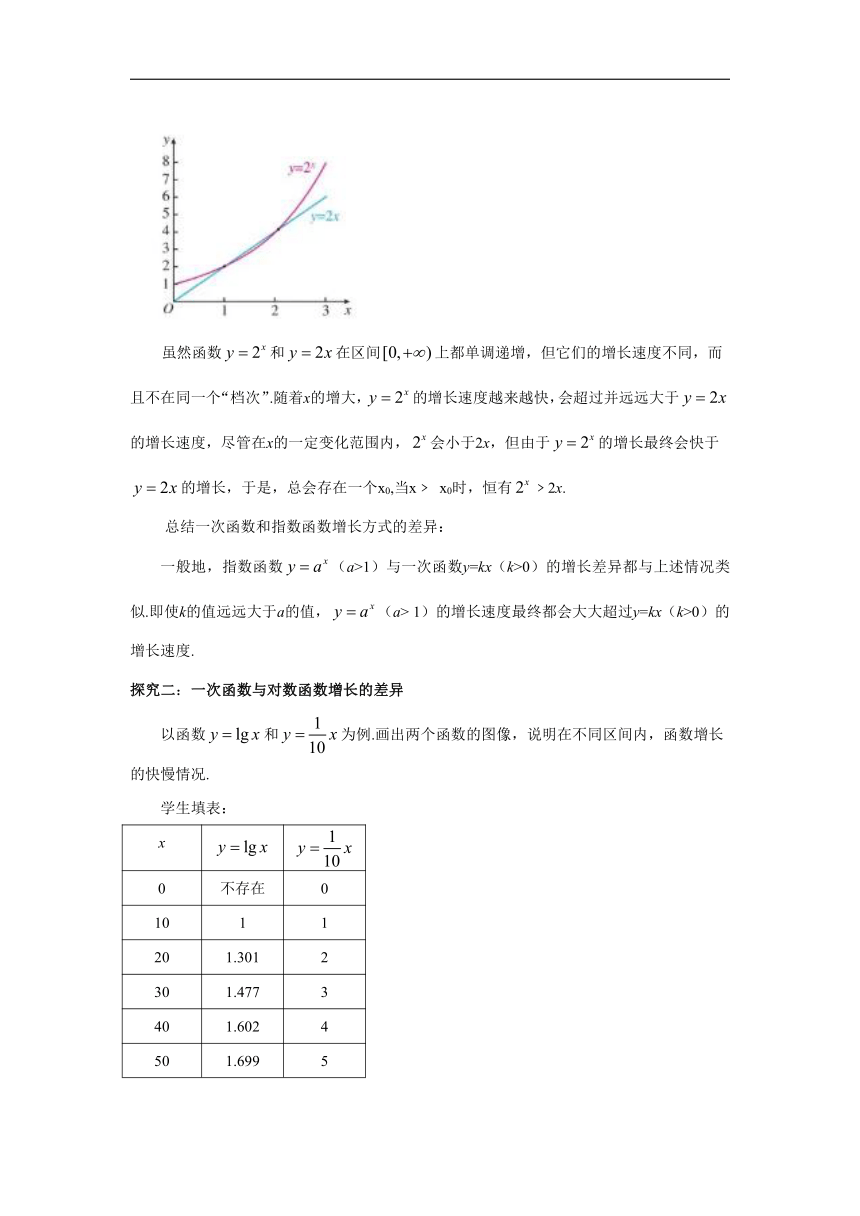
(一)探究一:一次函数与指数函数增长的差异
以函数和为例.画出两个函数的图像,说明在不同区间内,函数增长的快慢情况.
x
0 1 0
0.5 1.414 1
1 2 2
1.5 2.828 3
2 4 4
2.5 5.657 5
3 8 6
…. …. ….
在同一直角坐标系中画出函数图像如下:
虽然函数和在区间上都单调递增,但它们的增长速度不同,而且不在同一个“档次”.随着x的增大,的增长速度越来越快,会超过并远远大于的增长速度,尽管在x的一定变化范围内,会小于2x,但由于的增长最终会快于的增长,于是,总会存在一个x0,当x﹥ x0时,恒有﹥2x.
总结一次函数和指数函数增长方式的差异:
一般地,指数函数(a>1)与一次函数y=kx(k>0)的增长差异都与上述情况类似.即使k的值远远大于a的值,(a> 1)的增长速度最终都会大大超过y=kx(k>0)的增长速度.
探究二:一次函数与对数函数增长的差异
以函数和为例.画出两个函数的图像,说明在不同区间内,函数增长的快慢情况.
学生填表:
x
0 不存在 0
10 1 1
20 1.301 2
30 1.477 3
40 1.602 4
50 1.699 5
60 1.778 6
…. …. ….
在同一直角坐标系中画出函数图像如下:
观察研究函数和的增长快慢.
虽然函数和在区间上都单调递增,但它们的增长速度存在明显差异,函数的增长速度不变,而的增长速度在变化.随着x的增大,函数的图像越来越平缓,像与x轴平行一样.函数的图像离x轴越来越远.
总结一次函数和对数函数增长方式的差异:
一般地,虽然对数函数(a>1)与一次函数y=kx(k>0)在区间上都单调递增,但它们的增长速度不同. 随着x的增大,一次函数y=kx(k>0)保持着固定的增长速度,而对数函数(a>1)的增长速度越来越慢,不论a的值比k的值大多少,在一定范围内,可能会大于kx,但是由于的增长慢于kx的增长,于是,总会存在一个x0,当x﹥ x0时,恒有﹤kx.
(二)课堂练习
1.下列函数中,增长速度越来越慢的是( )
A. B. C. D.
答案:B
解析:对于D,一次函数的增长速度不变,A、C中函数的增长速度越来越快,只有B中对数函数的增长速度越来越慢,符合题意.故选B.
2.四个物体同时从某一点出发向前运动,其路程关于时间的函数关系是,,,,如果它们一直运动下去,最终在最前面的物体具有的函数关系是( )
A. B. C. D.
答案:D
解析:由增长速度可知,当自变量充分大时,指数函数的值最大.故选D.
3.下表是函数值y随自变量x变化的一组数据,由此判断最可能的函数模型是( )
x 4 5 6 7 8 9 10
y 15 17 19 21 23 25 27
A.一次函数模型 B.二次函数模型 C.指数函数模型 D.对数函数模型
答案:A
解析:自变量x每增加1,函数值y增加2,函数值的增量是均匀的,故为线性函数,即最可能的函数模型是一次函数模型. 故选A.
4.物价上涨是当前的热门话题,特别是菜价,我国某部门为尽快稳定菜价,提出四种绿色运输方案.据预测,这四种方案均能在规定的时间T内完成预测的运输任务,各种方案的运输总量Q与时间t的函数关系如图所示,在这四种方案中,运输效率(单位时间的运输量)逐步提高的是( )
A. B.
C. D.
答案:B
解析:由运输效率(单位时间的运输量)逐步提高知,函数增长的速度越来越快,故函数的图象应一直是下凸的,故选B.
(三)小结作业
小结:
本节课我们主要学习了哪些内容
1.指数函数与一次函数增长方式的差异.
2. 对数函数与一次函数增长方式的差异.
四、板书设计
1.指数函数与一次函数增长方式的差异.
2. 对数函数与一次函数增长方式的差异.
4.4.3 不同函数增长的差异
教学设计
一、教学目标
1.结合具体函数图像,总结一次函数、指数函数、对数函数的增长差异.
2.通过图像,了解“直线上升”“对数增长”“指数爆炸”的含义.
二、教学重难点
1.教学重点
研究一次函数、指数函数、对数函数的增长差异.
2.教学难点
函数增长快慢的因素.
三、教学过程
(一)探究一:一次函数与指数函数增长的差异
以函数和为例.画出两个函数的图像,说明在不同区间内,函数增长的快慢情况.
x
0 1 0
0.5 1.414 1
1 2 2
1.5 2.828 3
2 4 4
2.5 5.657 5
3 8 6
…. …. ….
在同一直角坐标系中画出函数图像如下:
虽然函数和在区间上都单调递增,但它们的增长速度不同,而且不在同一个“档次”.随着x的增大,的增长速度越来越快,会超过并远远大于的增长速度,尽管在x的一定变化范围内,会小于2x,但由于的增长最终会快于的增长,于是,总会存在一个x0,当x﹥ x0时,恒有﹥2x.
总结一次函数和指数函数增长方式的差异:
一般地,指数函数(a>1)与一次函数y=kx(k>0)的增长差异都与上述情况类似.即使k的值远远大于a的值,(a> 1)的增长速度最终都会大大超过y=kx(k>0)的增长速度.
探究二:一次函数与对数函数增长的差异
以函数和为例.画出两个函数的图像,说明在不同区间内,函数增长的快慢情况.
学生填表:
x
0 不存在 0
10 1 1
20 1.301 2
30 1.477 3
40 1.602 4
50 1.699 5
60 1.778 6
…. …. ….
在同一直角坐标系中画出函数图像如下:
观察研究函数和的增长快慢.
虽然函数和在区间上都单调递增,但它们的增长速度存在明显差异,函数的增长速度不变,而的增长速度在变化.随着x的增大,函数的图像越来越平缓,像与x轴平行一样.函数的图像离x轴越来越远.
总结一次函数和对数函数增长方式的差异:
一般地,虽然对数函数(a>1)与一次函数y=kx(k>0)在区间上都单调递增,但它们的增长速度不同. 随着x的增大,一次函数y=kx(k>0)保持着固定的增长速度,而对数函数(a>1)的增长速度越来越慢,不论a的值比k的值大多少,在一定范围内,可能会大于kx,但是由于的增长慢于kx的增长,于是,总会存在一个x0,当x﹥ x0时,恒有﹤kx.
(二)课堂练习
1.下列函数中,增长速度越来越慢的是( )
A. B. C. D.
答案:B
解析:对于D,一次函数的增长速度不变,A、C中函数的增长速度越来越快,只有B中对数函数的增长速度越来越慢,符合题意.故选B.
2.四个物体同时从某一点出发向前运动,其路程关于时间的函数关系是,,,,如果它们一直运动下去,最终在最前面的物体具有的函数关系是( )
A. B. C. D.
答案:D
解析:由增长速度可知,当自变量充分大时,指数函数的值最大.故选D.
3.下表是函数值y随自变量x变化的一组数据,由此判断最可能的函数模型是( )
x 4 5 6 7 8 9 10
y 15 17 19 21 23 25 27
A.一次函数模型 B.二次函数模型 C.指数函数模型 D.对数函数模型
答案:A
解析:自变量x每增加1,函数值y增加2,函数值的增量是均匀的,故为线性函数,即最可能的函数模型是一次函数模型. 故选A.
4.物价上涨是当前的热门话题,特别是菜价,我国某部门为尽快稳定菜价,提出四种绿色运输方案.据预测,这四种方案均能在规定的时间T内完成预测的运输任务,各种方案的运输总量Q与时间t的函数关系如图所示,在这四种方案中,运输效率(单位时间的运输量)逐步提高的是( )
A. B.
C. D.
答案:B
解析:由运输效率(单位时间的运输量)逐步提高知,函数增长的速度越来越快,故函数的图象应一直是下凸的,故选B.
(三)小结作业
小结:
本节课我们主要学习了哪些内容
1.指数函数与一次函数增长方式的差异.
2. 对数函数与一次函数增长方式的差异.
四、板书设计
1.指数函数与一次函数增长方式的差异.
2. 对数函数与一次函数增长方式的差异.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
