2.4线段的垂直平分线 优生辅导训练 2021-2022学年湘教版八年级数学上册(word版含答案)
文档属性
| 名称 | 2.4线段的垂直平分线 优生辅导训练 2021-2022学年湘教版八年级数学上册(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 225.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-16 08:58:38 | ||
图片预览



文档简介
2021-2022学年湘教版八年级数学上册《2.4线段的垂直平分线》优生辅导训练(附答案)
1.如图,△ABC中,BD平分∠ABC,E是BC的中点,过点E作BC的垂线交BD于点F,连接CF,若∠DFC=60°,∠ACF=40°,则∠A的度数为( )
A.45° B.50° C.55° D.60°
2.如图,△ABC中,∠C=90°,ED垂直平分AB,若AC=12,EC=5,且△ACE的周长为30,则BE的长为( )
A.5 B.10 C.12 D.13
3.如图△ABC中,AC=12,DE为AB的垂直平分线,△BCE的周长为20,则BC的长为( )
A.6 B.8 C.10 D.12
4.已知:如图,在△ABC中,边AB的垂直平分线分别交BC、AB于点G、D,若△AGC的周长为31cm,AB=20cm,则△ABC的周长为( )
A.31cm B.41cm C.51cm D.61cm
5.如图,线段AB,DE的垂直平分线交于点C,且∠ABC=∠EDC=72°,∠AEB=92°,则∠EBD的度数为( )
A.168° B.158° C.128° D.118°
6.如图所示,在△ABC中,内角∠BAC与外角∠CBE的平分线相交于点P,BE=BC,PB与CE交于点H,PG∥AD交BC于F,交AB于G,连接CP.下列结论:①∠ACB=2∠APB;②S△PAC:S△PAB=AC:AB;③BP垂直平分CE;④∠PCF=∠CPF.其中,正确的有( )
A.1个 B.2个 C.3个 D.4个
7.如图,△ABC中,EF是AB的垂直平分线,与AB交于点D,BF=10,CF=2,则AC= .
8.如图,在△ABC中,∠B=55°,∠C=28°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为 .
9.如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E,若BC=3,则DE的长为 .
10.如图在△ABC中MP,NQ分别垂直平分AB、AC,若BC的长度为9,则△APQ的周长是 .
11.如图,在△ABC中,DE是AC的垂直平分线且分别交BC,AC于点D和E,∠B=60°,∠C=25°,则∠BAD的度数为 .
12.如图,在△ABC中,已知点O是边AB、AC垂直平分线的交点,点E是∠ABC、∠ACB角平分线的交点,若∠O+∠E=180°,则∠A= 度.
13.如图,DE是AB的垂直平分线.
(1)已知AC=5cm,△ADC的周长为17cm,则BC的长
(2)若AD平分∠BAC,AD=AC,则∠C=
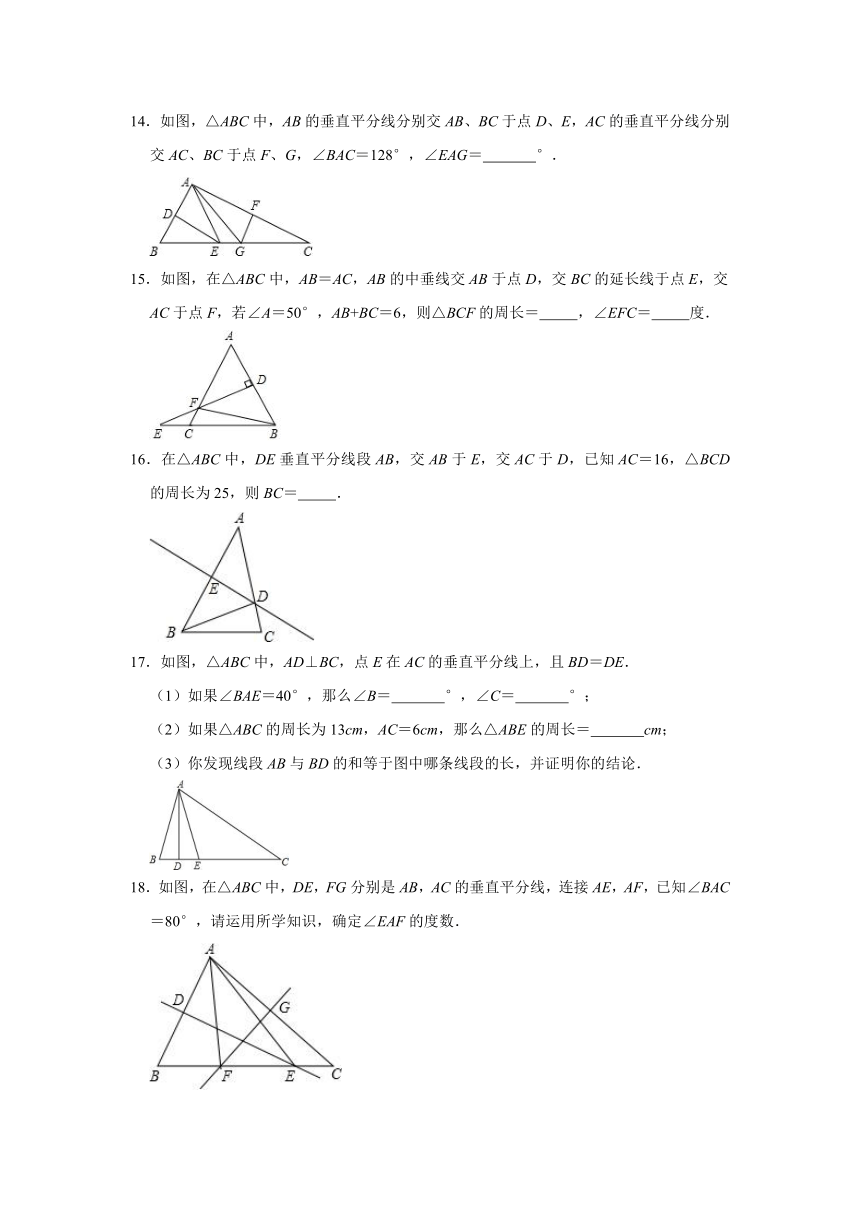
14.如图,△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G,∠BAC=128°,∠EAG= °.
15.如图,在△ABC中,AB=AC,AB的中垂线交AB于点D,交BC的延长线于点E,交AC于点F,若∠A=50°,AB+BC=6,则△BCF的周长= ,∠EFC= 度.
16.在△ABC中,DE垂直平分线段AB,交AB于E,交AC于D,已知AC=16,△BCD的周长为25,则BC= .
17.如图,△ABC中,AD⊥BC,点E在AC的垂直平分线上,且BD=DE.
(1)如果∠BAE=40°,那么∠B= °,∠C= °;
(2)如果△ABC的周长为13cm,AC=6cm,那么△ABE的周长= cm;
(3)你发现线段AB与BD的和等于图中哪条线段的长,并证明你的结论.
18.如图,在△ABC中,DE,FG分别是AB,AC的垂直平分线,连接AE,AF,已知∠BAC=80°,请运用所学知识,确定∠EAF的度数.
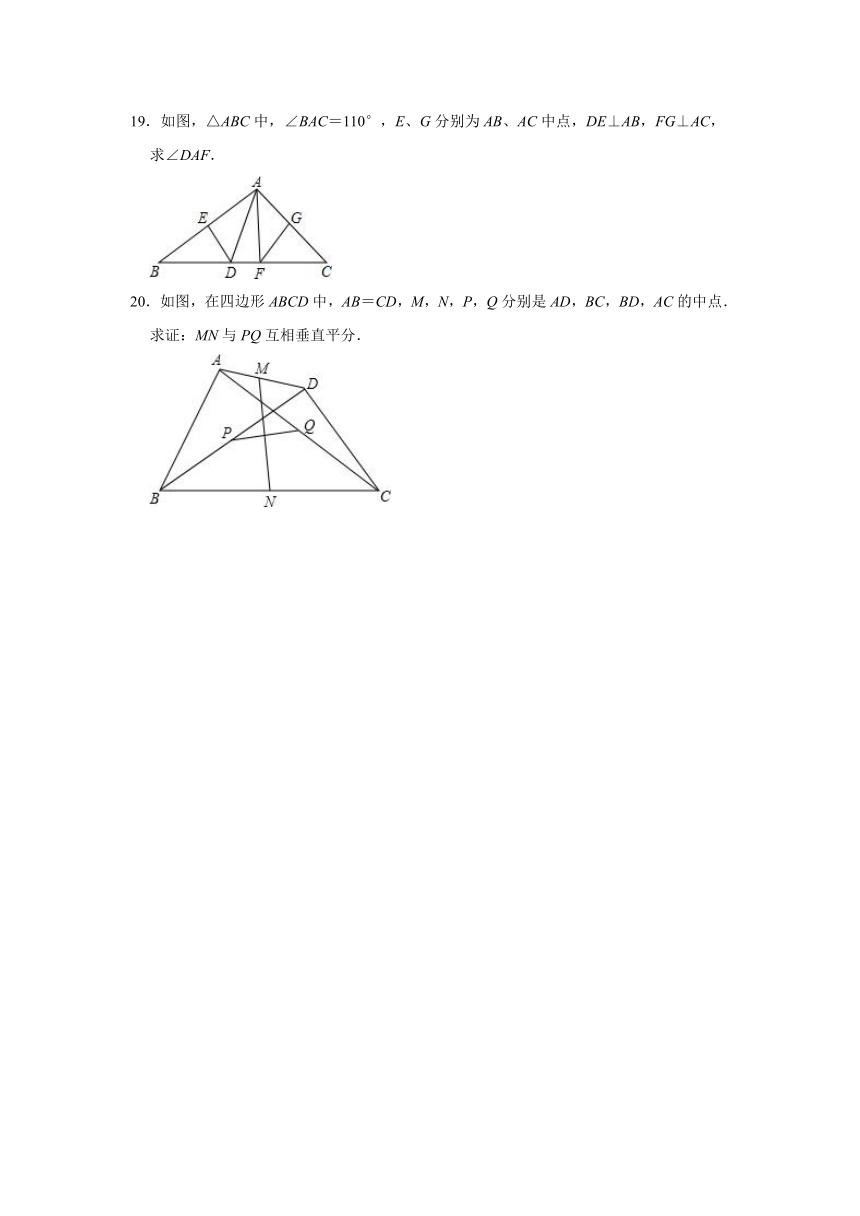
19.如图,△ABC中,∠BAC=110°,E、G分别为AB、AC中点,DE⊥AB,FG⊥AC,
求∠DAF.
20.如图,在四边形ABCD中,AB=CD,M,N,P,Q分别是AD,BC,BD,AC的中点.
求证:MN与PQ互相垂直平分.
参考答案
1.解:∵E是BC的中点,过点E作BC的垂线交BD于点F,
∴FE垂直平分BC,
∴BF=CF,
∴∠FBC=∠FCB,
∵∠CFD=∠FBC+∠FCB=60°,
∴∠FBC=∠FCB=30°,
∵∠ACF=40°,
∴∠ACB=∠ACF+∠BCF=70°,
∵BD平分∠ABC,
∴∠ABC=2∠FBC=60°,
∴∠A=180°﹣∠ABC﹣∠ACB=50°,
故选:B.
2.解:∵ED垂直平分AB,
∴BE=AE,
∵AC=12,EC=5,且△ACE的周长为30,
∴12+5+AE=30,
∴AE=13,
∴BE=AE=13,
故选:D.
3.解:∵DE为AB的垂直平分线,
∴AE=BE,
∵△BCE的周长为20,
∴BC+BE+CE=BC+AE+CE=BC+AC=20cm,
∵AC=12,
∴BC=8.
故选:B.
4.解:∵DG是AB的垂直平分线,
∴GA=GB,
∵△AGC的周长为31cm,
∴AG+GC+AC=BC+AC=31cm,又AB=20cm,
∴△ABC的周长=AB+AC+BC=51cm,
故选:C.
5.解:如图,连接CE,
∵线段AB,DE的垂直平分线交于点C,
∴CA=CB,CE=CD,
∵∠ABC=∠EDC=72°=∠DEC,
∴∠ACB=∠ECD=36°,
∴∠ACE=∠BCD,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(SAS),
∴∠AEC=∠BDC,
设∠AEC=∠BDC=α,则∠BDE=72°﹣α,∠CEB=92°﹣α,
∴∠BED=∠DEC﹣∠CEB=72°﹣(92°﹣α)=α﹣20°,
∴△BDE中,∠EBD=180°﹣(72°﹣α)﹣(α﹣20°)=128°,
故选:C.
6.解:∵PA平分∠CAB,PB平分∠CBE,
∴∠PAB=∠CAB,∠PBE=∠CBE,
∵∠CBE=∠CAB+∠ACB,
∠PBE=∠PAB+∠APB,
∴∠ACB=2∠APB;故①正确;
过P作PM⊥AB于M,PN⊥AC于N,PS⊥BC于S,
∴PM=PN=PS,
∴PC平分∠BCD,
∵S△PAC:S△PAB=(AC PN):(AB PM)=AC:AB;故②正确;
∵BE=BC,BP平分∠CBE
∴BP垂直平分CE(三线合一),故③正确;
∵PG∥AD,
∴∠FPC=∠DCP
∵PC平分∠DCB,
∴∠DCP=∠PCF,
∴∠PCF=∠CPF,故④正确.
故选:D.
7.解:∵EF是AB的垂直平分线,
∴FA=BF=10,
∴AC=AF+FC=12.
故答案为:12.
8.解:∵△ABC中,∠B=55°,∠C=28°,
∴∠BAC=180°﹣55°﹣28°=97°.
∵直线MN是线段AC的垂直平分线,
∴∠C=∠CAD=28°,
∴∠BAD=∠BAC﹣∠CAD=97°﹣28°=69°.
故答案为:69°.
9.解:∵DE是AB的垂直平分线,
∴DA=DB,
∴∠B=∠DAB,
∵AD是∠CAB的平分线,
∴∠DAC=∠DAB,
∴∠B=30°,
∴DE=BD,
∵AD是∠CAB的平分线,∠C=90°,DE⊥AB,
∴DE=DC,
∴DC=BD,
∴DC=1,即DE=1,
故答案为:1.
10.解:∵在△ABC中,MP,NO分别垂直平分AB、AC,
∴AP=BP,AQ=CQ,
∵BC=9,
∴△APQ的周长是AP+PQ+AQ=BP+PQ+CQ=BC=9,
故答案为:9.
11.解:∵DE是AC的垂直平分线且分别交BC,AC于点D和E,
∴AD=CD,
∴∠C=∠DAC,
∵∠C=25°,
∴∠DAC=25°,
∵在△ABC中,∠B=60°,∠C=25°,
∴∠BAC=180°﹣∠B﹣∠C=95°,
∴∠BAD=∠BAC﹣∠DAC=95°﹣25°=70°,
故答案为:70°.
12.解:如图,连接OA.
∵点O是AB,AC的垂直平分线的交点,
∴OA=OB=OC,
∴∠OAB=∠OBA,∠OAC=∠OCA,
∵∠BOC=∠ABO+∠OCA+∠BAC=2∠OAB+2∠OAC=2∠BAC,
∵点E是∠ABC、∠ACB角平分线的交点,
∴∠E=90°+∠BAC,
∵∠BOC+∠E=180°,
∴2∠BAC+90°+∠BAC=180°,
∴∠BAC=36°,
故答案为36.
13.解:(1)∵DE垂直平分线线段AB,
∴DA=DB,
∵AD+CD+AC=17,AC=5,
∴BD+CD+AC=17,
∴BC+AC=17,
∴BC=17﹣5=12cm,
故答案为12cm.
(2)设∠DAB=∠DAC=x,
∵DA=DB,
∴∠DBA=∠DAB=x,
∴∠ADC=∠B+∠DAB=2x,
∵AD=AC,
∴∠C=∠ADC=2x,
∴5x=180°,
∴x=36°,
∴∠C=72°,
故答案为72°.
14.解:∵∠BAC=128°,
∴∠A+∠B=180°﹣128°=52°,
∵DE是AB的垂直平分线,
∴EA=EB,
∴∠EAB=∠B,
同理∠GAC=∠C,
∴∠EAB+∠GAC=∠A+∠B=52°,
∴∠EAG=128°﹣52°=76°,
故答案为:76.
15.解:如图:已知DF垂直且平分AB AF=BF,AD=BD,∠A=∠ABF=50°,∠ADF=90°
∠EFC=180°﹣∠A﹣∠ADF=40°(对角相等)
因为AB+BC=6,AB=AC=BF+FC
故周长△BCF=FC+BF+BC=6.
故填6;40°.
16.解:∵DE垂直平分线段AB,
∴AD=BD,
∵△BCD的周长为25,
∴BD+CD+BC=AD+CD+BC=AC+BC=25,
∵AC=16,
∴BC=9.
故答案为:9.
17.(1)解:∵点E在AC的垂直平分线上,
∴AE=EC.
∵BD=DE,AD⊥BC,
∴AB=AE.
∴∠ABE=∠AEB=2∠C=(180°﹣40°)÷2=140°÷2=70°,∠C=35°.
故答案为:70,35;
(2)解:∵△ABC的周长为13cm,AC=6cm,
∴AB+BC=13﹣6=7,
∴△ABE的周长=AB+BC=7cm.
故答案为:7;
(3)AB+BD=DC.
证明:∵AD⊥BC,BD=DE,
∴AB=AE,BD=DE,
∵点E在AC的垂直平分线上,
∴AE=CE,
∴AB+BD=AE+DE=DC.
18.解:在△ABC中,∠BAC=80°,
∴∠B+∠C=180°﹣∠BAC=100°,
∵DE是AB的垂直平分线,
∴EB=EA,
∴∠BAE=∠B,
同理可得∠CAF=∠C,
∴∠EAF=∠BAE+∠CAF﹣∠BAC=∠B+∠C﹣∠BAC=20°.
19.解:∵∠BAC=110°,
∴∠B+∠C=180°﹣110°=70°,
∵E、G分别为AB、AC中点,DE⊥AB,FG⊥AC,
∴AD=BD,AF=CF,
∴∠BAD=∠B,∠CAF=∠C,
∴∠DAF=∠BAC﹣(∠BAD+∠CAF)=∠BAC﹣(∠B+∠C)=110°﹣70°=40°.
20.证明:连接MP,PN,NQ,QM,
∵AM=MD,BP=PD,
∴PM=AB,
∴PM是△ABD的中位线,
∴PM∥AB;
同理NQ=AB,NQ∥AB,MQ=DC,
∴PM=NQ,且PM∥NQ.
∴四边形MPNQ是平行四边形.
又∵AB=DC,∴PM=MQ,
∴平行四边形MPNQ是菱形.
∴MN与PQ互相垂直平分.
1.如图,△ABC中,BD平分∠ABC,E是BC的中点,过点E作BC的垂线交BD于点F,连接CF,若∠DFC=60°,∠ACF=40°,则∠A的度数为( )
A.45° B.50° C.55° D.60°
2.如图,△ABC中,∠C=90°,ED垂直平分AB,若AC=12,EC=5,且△ACE的周长为30,则BE的长为( )
A.5 B.10 C.12 D.13
3.如图△ABC中,AC=12,DE为AB的垂直平分线,△BCE的周长为20,则BC的长为( )
A.6 B.8 C.10 D.12
4.已知:如图,在△ABC中,边AB的垂直平分线分别交BC、AB于点G、D,若△AGC的周长为31cm,AB=20cm,则△ABC的周长为( )
A.31cm B.41cm C.51cm D.61cm
5.如图,线段AB,DE的垂直平分线交于点C,且∠ABC=∠EDC=72°,∠AEB=92°,则∠EBD的度数为( )
A.168° B.158° C.128° D.118°
6.如图所示,在△ABC中,内角∠BAC与外角∠CBE的平分线相交于点P,BE=BC,PB与CE交于点H,PG∥AD交BC于F,交AB于G,连接CP.下列结论:①∠ACB=2∠APB;②S△PAC:S△PAB=AC:AB;③BP垂直平分CE;④∠PCF=∠CPF.其中,正确的有( )
A.1个 B.2个 C.3个 D.4个
7.如图,△ABC中,EF是AB的垂直平分线,与AB交于点D,BF=10,CF=2,则AC= .
8.如图,在△ABC中,∠B=55°,∠C=28°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为 .
9.如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E,若BC=3,则DE的长为 .
10.如图在△ABC中MP,NQ分别垂直平分AB、AC,若BC的长度为9,则△APQ的周长是 .
11.如图,在△ABC中,DE是AC的垂直平分线且分别交BC,AC于点D和E,∠B=60°,∠C=25°,则∠BAD的度数为 .
12.如图,在△ABC中,已知点O是边AB、AC垂直平分线的交点,点E是∠ABC、∠ACB角平分线的交点,若∠O+∠E=180°,则∠A= 度.
13.如图,DE是AB的垂直平分线.
(1)已知AC=5cm,△ADC的周长为17cm,则BC的长
(2)若AD平分∠BAC,AD=AC,则∠C=
14.如图,△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G,∠BAC=128°,∠EAG= °.
15.如图,在△ABC中,AB=AC,AB的中垂线交AB于点D,交BC的延长线于点E,交AC于点F,若∠A=50°,AB+BC=6,则△BCF的周长= ,∠EFC= 度.
16.在△ABC中,DE垂直平分线段AB,交AB于E,交AC于D,已知AC=16,△BCD的周长为25,则BC= .
17.如图,△ABC中,AD⊥BC,点E在AC的垂直平分线上,且BD=DE.
(1)如果∠BAE=40°,那么∠B= °,∠C= °;
(2)如果△ABC的周长为13cm,AC=6cm,那么△ABE的周长= cm;
(3)你发现线段AB与BD的和等于图中哪条线段的长,并证明你的结论.
18.如图,在△ABC中,DE,FG分别是AB,AC的垂直平分线,连接AE,AF,已知∠BAC=80°,请运用所学知识,确定∠EAF的度数.
19.如图,△ABC中,∠BAC=110°,E、G分别为AB、AC中点,DE⊥AB,FG⊥AC,
求∠DAF.
20.如图,在四边形ABCD中,AB=CD,M,N,P,Q分别是AD,BC,BD,AC的中点.
求证:MN与PQ互相垂直平分.
参考答案
1.解:∵E是BC的中点,过点E作BC的垂线交BD于点F,
∴FE垂直平分BC,
∴BF=CF,
∴∠FBC=∠FCB,
∵∠CFD=∠FBC+∠FCB=60°,
∴∠FBC=∠FCB=30°,
∵∠ACF=40°,
∴∠ACB=∠ACF+∠BCF=70°,
∵BD平分∠ABC,
∴∠ABC=2∠FBC=60°,
∴∠A=180°﹣∠ABC﹣∠ACB=50°,
故选:B.
2.解:∵ED垂直平分AB,
∴BE=AE,
∵AC=12,EC=5,且△ACE的周长为30,
∴12+5+AE=30,
∴AE=13,
∴BE=AE=13,
故选:D.
3.解:∵DE为AB的垂直平分线,
∴AE=BE,
∵△BCE的周长为20,
∴BC+BE+CE=BC+AE+CE=BC+AC=20cm,
∵AC=12,
∴BC=8.
故选:B.
4.解:∵DG是AB的垂直平分线,
∴GA=GB,
∵△AGC的周长为31cm,
∴AG+GC+AC=BC+AC=31cm,又AB=20cm,
∴△ABC的周长=AB+AC+BC=51cm,
故选:C.
5.解:如图,连接CE,
∵线段AB,DE的垂直平分线交于点C,
∴CA=CB,CE=CD,
∵∠ABC=∠EDC=72°=∠DEC,
∴∠ACB=∠ECD=36°,
∴∠ACE=∠BCD,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(SAS),
∴∠AEC=∠BDC,
设∠AEC=∠BDC=α,则∠BDE=72°﹣α,∠CEB=92°﹣α,
∴∠BED=∠DEC﹣∠CEB=72°﹣(92°﹣α)=α﹣20°,
∴△BDE中,∠EBD=180°﹣(72°﹣α)﹣(α﹣20°)=128°,
故选:C.
6.解:∵PA平分∠CAB,PB平分∠CBE,
∴∠PAB=∠CAB,∠PBE=∠CBE,
∵∠CBE=∠CAB+∠ACB,
∠PBE=∠PAB+∠APB,
∴∠ACB=2∠APB;故①正确;
过P作PM⊥AB于M,PN⊥AC于N,PS⊥BC于S,
∴PM=PN=PS,
∴PC平分∠BCD,
∵S△PAC:S△PAB=(AC PN):(AB PM)=AC:AB;故②正确;
∵BE=BC,BP平分∠CBE
∴BP垂直平分CE(三线合一),故③正确;
∵PG∥AD,
∴∠FPC=∠DCP
∵PC平分∠DCB,
∴∠DCP=∠PCF,
∴∠PCF=∠CPF,故④正确.
故选:D.
7.解:∵EF是AB的垂直平分线,
∴FA=BF=10,
∴AC=AF+FC=12.
故答案为:12.
8.解:∵△ABC中,∠B=55°,∠C=28°,
∴∠BAC=180°﹣55°﹣28°=97°.
∵直线MN是线段AC的垂直平分线,
∴∠C=∠CAD=28°,
∴∠BAD=∠BAC﹣∠CAD=97°﹣28°=69°.
故答案为:69°.
9.解:∵DE是AB的垂直平分线,
∴DA=DB,
∴∠B=∠DAB,
∵AD是∠CAB的平分线,
∴∠DAC=∠DAB,
∴∠B=30°,
∴DE=BD,
∵AD是∠CAB的平分线,∠C=90°,DE⊥AB,
∴DE=DC,
∴DC=BD,
∴DC=1,即DE=1,
故答案为:1.
10.解:∵在△ABC中,MP,NO分别垂直平分AB、AC,
∴AP=BP,AQ=CQ,
∵BC=9,
∴△APQ的周长是AP+PQ+AQ=BP+PQ+CQ=BC=9,
故答案为:9.
11.解:∵DE是AC的垂直平分线且分别交BC,AC于点D和E,
∴AD=CD,
∴∠C=∠DAC,
∵∠C=25°,
∴∠DAC=25°,
∵在△ABC中,∠B=60°,∠C=25°,
∴∠BAC=180°﹣∠B﹣∠C=95°,
∴∠BAD=∠BAC﹣∠DAC=95°﹣25°=70°,
故答案为:70°.
12.解:如图,连接OA.
∵点O是AB,AC的垂直平分线的交点,
∴OA=OB=OC,
∴∠OAB=∠OBA,∠OAC=∠OCA,
∵∠BOC=∠ABO+∠OCA+∠BAC=2∠OAB+2∠OAC=2∠BAC,
∵点E是∠ABC、∠ACB角平分线的交点,
∴∠E=90°+∠BAC,
∵∠BOC+∠E=180°,
∴2∠BAC+90°+∠BAC=180°,
∴∠BAC=36°,
故答案为36.
13.解:(1)∵DE垂直平分线线段AB,
∴DA=DB,
∵AD+CD+AC=17,AC=5,
∴BD+CD+AC=17,
∴BC+AC=17,
∴BC=17﹣5=12cm,
故答案为12cm.
(2)设∠DAB=∠DAC=x,
∵DA=DB,
∴∠DBA=∠DAB=x,
∴∠ADC=∠B+∠DAB=2x,
∵AD=AC,
∴∠C=∠ADC=2x,
∴5x=180°,
∴x=36°,
∴∠C=72°,
故答案为72°.
14.解:∵∠BAC=128°,
∴∠A+∠B=180°﹣128°=52°,
∵DE是AB的垂直平分线,
∴EA=EB,
∴∠EAB=∠B,
同理∠GAC=∠C,
∴∠EAB+∠GAC=∠A+∠B=52°,
∴∠EAG=128°﹣52°=76°,
故答案为:76.
15.解:如图:已知DF垂直且平分AB AF=BF,AD=BD,∠A=∠ABF=50°,∠ADF=90°
∠EFC=180°﹣∠A﹣∠ADF=40°(对角相等)
因为AB+BC=6,AB=AC=BF+FC
故周长△BCF=FC+BF+BC=6.
故填6;40°.
16.解:∵DE垂直平分线段AB,
∴AD=BD,
∵△BCD的周长为25,
∴BD+CD+BC=AD+CD+BC=AC+BC=25,
∵AC=16,
∴BC=9.
故答案为:9.
17.(1)解:∵点E在AC的垂直平分线上,
∴AE=EC.
∵BD=DE,AD⊥BC,
∴AB=AE.
∴∠ABE=∠AEB=2∠C=(180°﹣40°)÷2=140°÷2=70°,∠C=35°.
故答案为:70,35;
(2)解:∵△ABC的周长为13cm,AC=6cm,
∴AB+BC=13﹣6=7,
∴△ABE的周长=AB+BC=7cm.
故答案为:7;
(3)AB+BD=DC.
证明:∵AD⊥BC,BD=DE,
∴AB=AE,BD=DE,
∵点E在AC的垂直平分线上,
∴AE=CE,
∴AB+BD=AE+DE=DC.
18.解:在△ABC中,∠BAC=80°,
∴∠B+∠C=180°﹣∠BAC=100°,
∵DE是AB的垂直平分线,
∴EB=EA,
∴∠BAE=∠B,
同理可得∠CAF=∠C,
∴∠EAF=∠BAE+∠CAF﹣∠BAC=∠B+∠C﹣∠BAC=20°.
19.解:∵∠BAC=110°,
∴∠B+∠C=180°﹣110°=70°,
∵E、G分别为AB、AC中点,DE⊥AB,FG⊥AC,
∴AD=BD,AF=CF,
∴∠BAD=∠B,∠CAF=∠C,
∴∠DAF=∠BAC﹣(∠BAD+∠CAF)=∠BAC﹣(∠B+∠C)=110°﹣70°=40°.
20.证明:连接MP,PN,NQ,QM,
∵AM=MD,BP=PD,
∴PM=AB,
∴PM是△ABD的中位线,
∴PM∥AB;
同理NQ=AB,NQ∥AB,MQ=DC,
∴PM=NQ,且PM∥NQ.
∴四边形MPNQ是平行四边形.
又∵AB=DC,∴PM=MQ,
∴平行四边形MPNQ是菱形.
∴MN与PQ互相垂直平分.
同课章节目录
