2.5等腰三角形的判定与性质靶向训练2021-2022学年八年级上册数学 苏科版 (word版含答案)
文档属性
| 名称 | 2.5等腰三角形的判定与性质靶向训练2021-2022学年八年级上册数学 苏科版 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-16 08:59:22 | ||
图片预览


文档简介
2.5等腰三角形的判定与性质
考点一、等腰三角形的边与角的计算
如果等腰三角形的两边长分别为3和7,那么它的周长为______。
等腰三角形的一个内角为,则顶角的度数是______.
已知等腰三角形中有一个内角为,则该等腰三角形的底角为______.
已知等腰三角形的一个外角为,则它的顶角的度数为______.
一个等腰三角形的两边长分别为5和6,则这个等腰三角形的周长是 .
已知等腰三角形一腰上的高与另一腰的夹角为,则这个等腰三角形顶角的度数为______.
考点二、等腰三角形的性质
如图,在等腰三角形ABC中,,AD是边BC上的高,E是AD上一点.
求证:是等腰三角形;
若,,E是AD的中点,求的周长.
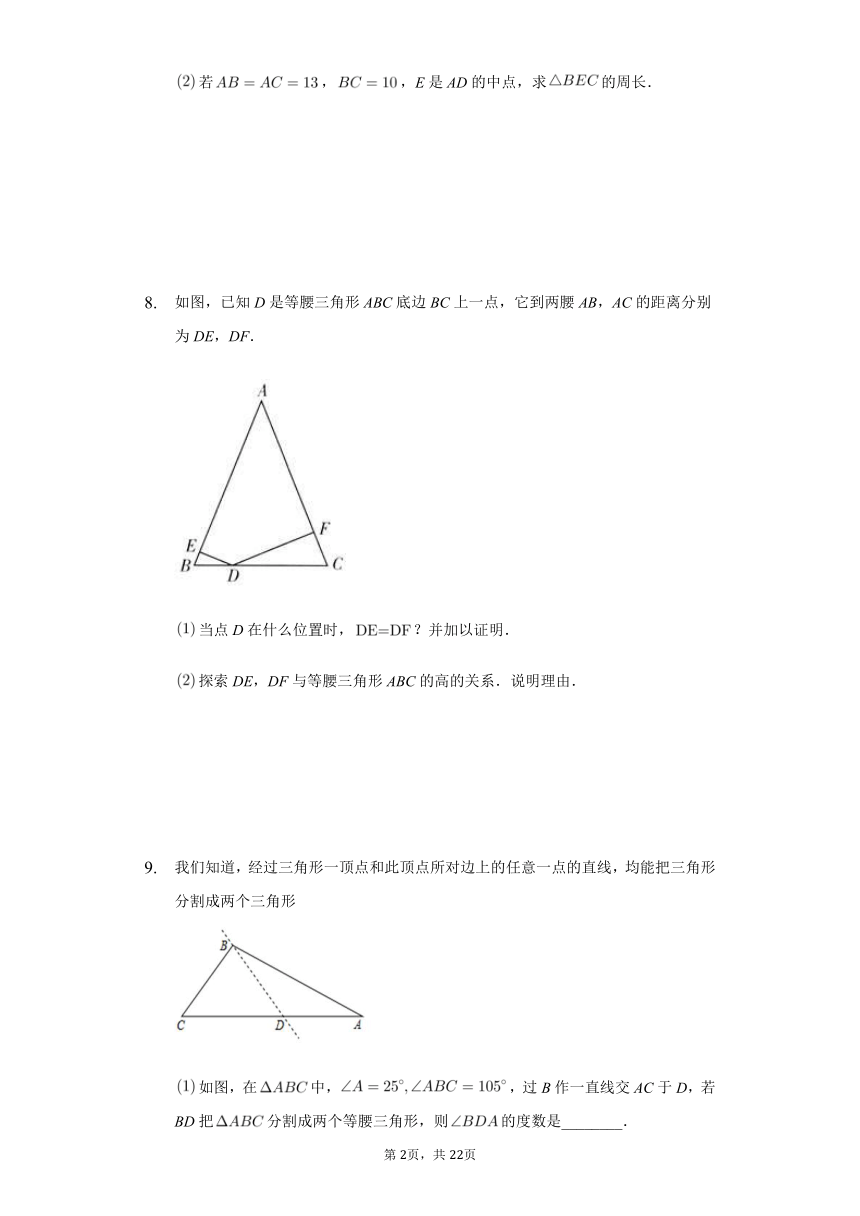
如图,已知D是等腰三角形ABC底边BC上一点,它到两腰AB,AC的距离分别为DE,DF.
当点D在什么位置时,?并加以证明.
探索DE,DF与等腰三角形ABC的高的关系.说明理由.
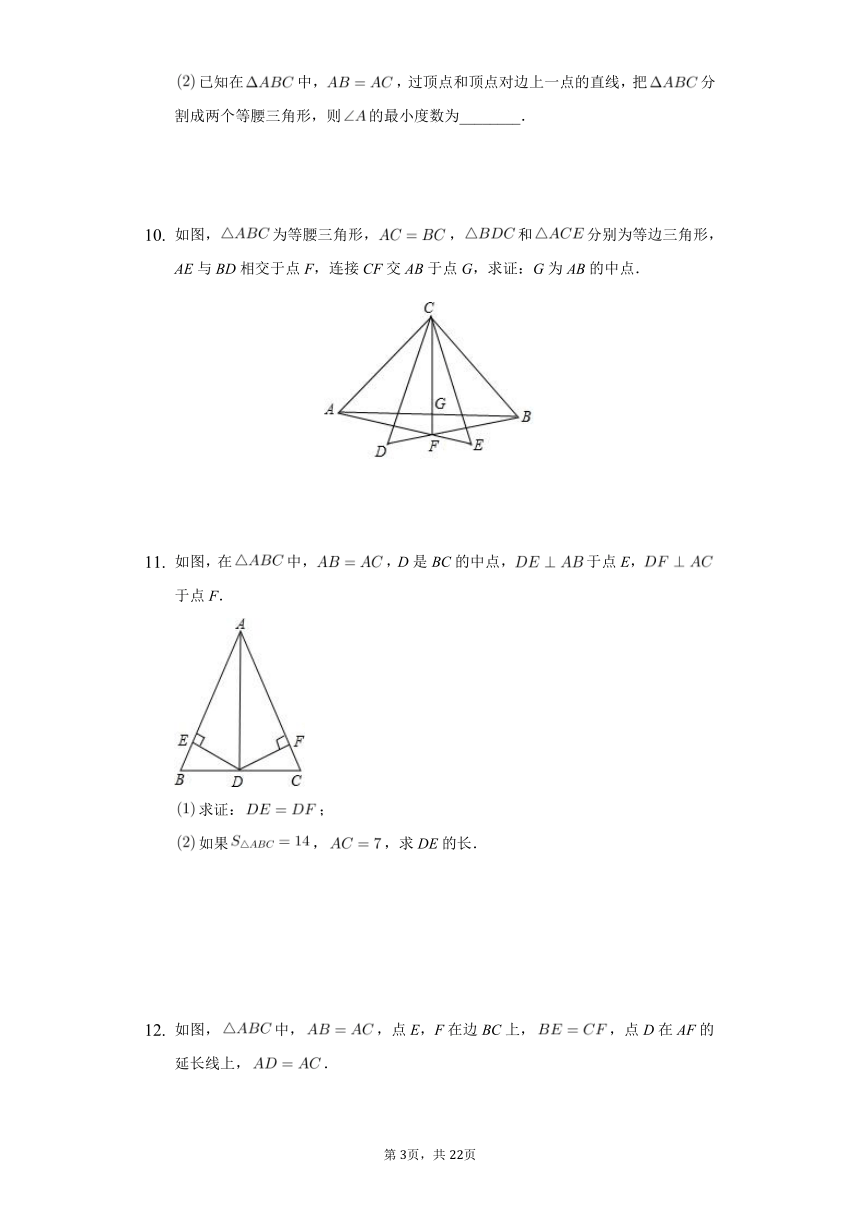
我们知道,经过三角形一顶点和此顶点所对边上的任意一点的直线,均能把三角形分割成两个三角形
如图,在中,,过B作一直线交AC于D,若BD把分割成两个等腰三角形,则的度数是________.
已知在中,,过顶点和顶点对边上一点的直线,把分割成两个等腰三角形,则的最小度数为________.
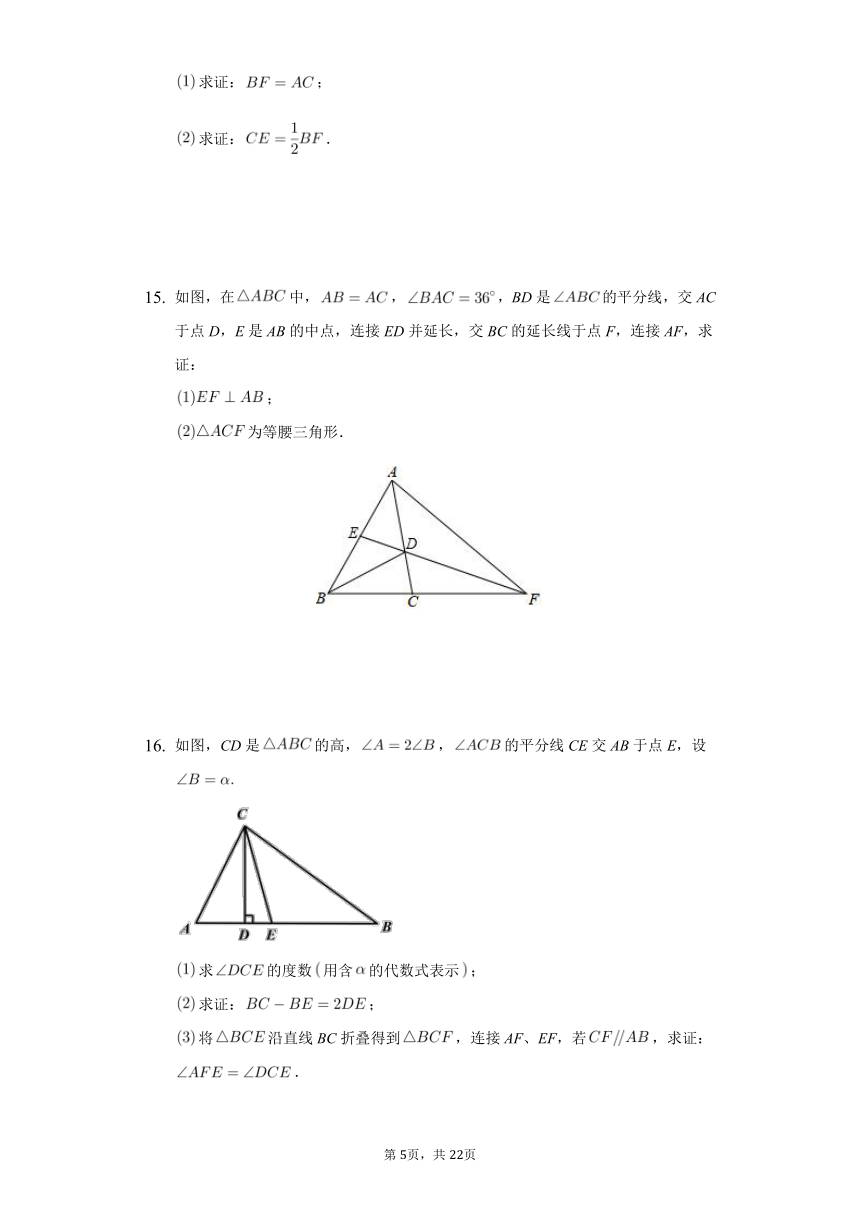
如图,为等腰三角形,,和分别为等边三角形,AE与BD相交于点F,连接CF交AB于点G,求证:G为AB的中点.
如图,在中,,D是BC的中点,于点E,于点F.
求证:;
如果,,求DE的长.
如图,中,,点E,F在边BC上,,点D在AF的延长线上,.
求证:≌;
若,则________.
考点三、等腰三角形的判定
如图,AD平分,,垂足为点D,.
求证:是等腰三角形.
已知:如图,中,,于D,BE平分,且于E,与CD相交于点F,H是BC边的中点,连结DH与BE相交于点G.
求证:;
求证:.
如图,在中,,,BD是的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF,求证:
;
为等腰三角形.
如图,CD是的高,,的平分线CE交AB于点E,设
求的度数用含的代数式表示;
求证:;
将沿直线BC折叠得到,连接AF、EF,若,求证:.
如图,在中,AD平分,交BC于点D.
尺规作图:作BE平分,分别交AC,AD于点E,I;
保留作图痕迹,不必写出作法
在的条件下,求证:点I在的平分线上;
若,,过点B作,垂足为点F,请画出符合条件的图形,猜想BF和AD的数量关系,并证明你的结论.
如图,在中,,D在边AC上,且.
如图1,填空______,______
如图2,若M为线段AC上的点,过M作直线于H,分别交直线AB、BC与点N、E.
求证:是等腰三角形;
试写出线段AN、CE、CD之间的数量关系,并加以证明.
答案和解析
1.【答案】17
【解析】
【分析】
题目给出等腰三角形有两条边长为3和7,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形。
【解答】
解:分两种情况讨论:
若3为腰长,7为底边长,
由于,则三角形不存在;
若7为腰长,则符合三角形的两边之和大于第三边,两边之差小于第三边。
所以这个三角形的周长为:。
故答案为17。
2.【答案】
【解析】解:,
的角是顶角,
故答案为:.
根据角是钝角判断出只能是顶角,然后根据等腰三角形两底角相等解答.
本题考查了等腰三角形两底角相等的性质,先判断出的角是顶角是解题的关键.
3.【答案】或
【解析】
【分析】
本题考查的是等腰三角形的性质及三角形内角和定理;解答此题时要注意的角是顶角和底角两种情况,不要漏解,分类讨论是正确解答本题的关键.由于不明确的角是等腰三角形的底角还是顶角,故应分的角是顶角和底角两种情况讨论.
【解答】
解:分两种情况:
当的角为等腰三角形的顶角时,
底角的度数;
当的角为等腰三角形的底角时,其底角为,
故它的底角度数是或.
故答案为或
4.【答案】或
【解析】解:当为顶角时,其他两角都为、,
当为底角时,其他两角为、,
所以等腰三角形的顶角为或.
故答案为:或.
等腰三角形的一个外角等于,则等腰三角形的一个内角为,但已知没有明确此角是顶角还是底角,所以应分两种情况进行分类讨论.
本题考查了等腰三角形的性质,及三角形内角和定理.
5.【答案】16或17
【解析】
【分析】
本题考查了等腰三角形的性质和三角形的三边关系.
由于未说明两边哪个是腰哪个是底,故需分:当等腰三角形的腰为当等腰三角形的腰为两种情况讨论,从而得到其周长.
【解答】
解:当等腰三角形的腰为5,底为6时,周长为;
当等腰三角形的腰为6,底为5时,周长为;
故这个等腰三角形的周长是16或17.
故答案为:16或17.
6.【答案】或
【解析】解:如图,
,,
,
,
;
如图,
,,
,
,
,
;
综上所述,它的顶角度数为:或.
故答案为:或.
分别从是锐角三角形与钝角三角形去分析求解即可求得答案.
此题考查了等腰三角形的性质.此题难度适中,注意掌握分类讨论思想的应用是解此题的关键.
7.【答案】在等腰三角形ABC中,,AD是边BC上的高,
.
垂直平分BC,
,即是等腰三角形;
是等腰三角形ABC的底边上的高,,
.
,
,
是AD的中点,
,
,
的周长是.
【解析】本题考查了等腰三角形的判定与性质、勾股定理及线段的垂直平分线的判定与性质,熟练掌握各定理的应用是解题关键.
根据等腰三角形的性质得到,根据线段垂直平分的性质得到,即可得证;
根据等腰三角形的性质得到CD的长,根据勾股定理得到AD的长,再根据勾股定理得到BE的长,即可得到的周长.
8.【答案】解:为中点时,,
理由是:如图,连接AD,
,D为BC中点,
平分,
,,
.
的长为腰上的高的长,
理由是:连接AD,过C作于M,
,
,
,
,
即的长为腰上的高的长.
【解析】本题考查了角平分线性质,等腰三角形性质,三角形面积的应用,题目具有一定的代表性,难度适中.
连接AD,根据三线合一定理求出AD平分,根据角平分线性质求出即可.
连接AD,过C作于M,根据三角形面积公式求出即可.
9.【答案】;
.
【解析】
【试题解析】
【分析】
本题主要考查等腰三角形的性质,三角形的内角和定理,注意分类讨论.
由可得,再根据三角形的内角和解答即可;
可分四种情况,利用等腰三角形的性质及三角形的内角和定理分别计算,即可求解的最小值.
【解答】
解:根据题意得,
,
.
故答案为;
如图1,,当,,
,
,
,
.
如图2,,,,
,,
,
,
,
,
.
如图3,,,
,,,
,
,
,
,
.
如图4,,,,
,,,
,
,
,
,
.
综上所述,的最小度数为.
10.【答案】证明:,
,
和为等边三角形,
,
,
.
在和中,
≌,
,
即CF平分,
又,
,
即G为AB的中点.
【解析】本题考查了全等三角形的判定与性质、等边三角形的性质以及等腰三角形三线合一的性质,证明三角形全等是解题的关键.
证明≌,可得,根据等腰三角形的性质即可解题.
11.【答案】解:证明:连接AD,如图,
,点D是BC边上的中点,
平分,
、DF分别垂直AB、AC于点E和F,
,点D是BC边上的中点,,
,
,
.
【解析】本题考查的是等腰三角形的性质、角平分线的性质、三角形的面积解题关键在于熟知等腰三角形三线合一的性质.
根据等腰三角形三线合一的特性,可得出AD也是的角平分线,根据角平分线的点到角两边的距离相等的性质即可得出答案
根据三角形中线的性质和三角形的面积解答即可得出答案.
12.【答案】解:,
,
在和中,
,
≌;
.
【解析】
【分析】
本题考查全等三角形的判定与性质,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
要证明≌,由题意可得,,,从而可以证明结论成立;
根据中的结论和等腰三角形的性质可以求得的度数.
【解答】
解:见答案;
≌,,
,
,
,
,
故答案为75.
13.【答案】证明:,
,
平分,
,
,
,
,,
,
,
是等腰三角形.
【解析】直接利用平行线的性质得出,进而利用角平分线的定义结合互余的性质得出,即可得出答案.
此题主要考查了平行线的性质以及角平分线的定义,正确得出是解题关键.
14.【答案】证明:,,
是等腰直角三角形.
.
,,且,
.
在和中,
,
≌,
.
证明:平分,
.
在和中,
,
≌.
,
又,
.
【解析】本题考查了三角形的内角和定理,等腰三角形的性质和判定,全等三角形的性质和判定的应用,关键是推出≌和≌,题目综合性比较强.
根据三角形的内角和定理求出,推出,根据AAS证出≌即可;
推出,,根据ASA证出≌,推出即可.
15.【答案】证明:,,
,
又是的平分线,
,
,
,
又是AB的中点,
,即;
,,
垂直平分AB,
,
,
又,
,
又,
,
,
,即为等腰三角形.
【解析】依据,,可得,再根据BD是的平分线,即可得到,由,可得,依据E是AB的中点,即可得到;
依据,,可得FE垂直平分AB,进而得出,依据,即可得到,再根据,可得,进而得到.
本题考查了等腰三角形的判定与性质,解决问题的关键是综合运用等腰三角形的判定与性质,线段垂直平分线的判定与性质,三角形外角的性质.
16.【答案】解:,,
,
平分,
,
是高,
,
.
证明:如图,在AD上截取,连接CH,
,
,
,,
,
,
,
;
如图,设EF交BC于点O,
,
,,
折叠的对称性,且E点的对称点为F点,
,,,
,
,解得,
由得,
,
,
,
,
,,
在中,,
由得,
.
【解析】本题考查三角形的内角和定理,角平分线的定义,平行线的性质,等腰三角形的判定和性质,折叠与对称,关键是掌握三角形的内角和定理,等腰三角形的判定和性质,轴对称的性质,正确应用有关性质即可解答.
根据角平分线的定义,三角形的内角和定理用含有的代数式分别表示、、、即可解答;
在AD上截取,连接CH,先根据等腰三角形的性质用含有的代数式分别表示、、、、得,再根据等腰三角形的判定和性质即可解答;
设EF交BC于点O,先根据平分线的性质得,,再根据轴对称的性质得,,,最后根据,得关于的方程,解方程求得的值即可求解得证.
17.【答案】如图1,线段BE就是所求作的角平分线;
证明:
如图1,过点I作,,,点F,G,H为垂足.
平分,,,
.
同理可得:.
,
,,
点I在的平分线上角的内部到角两边距离相等的点在角的平分线上.
和AD的数量关系是:或
证明如下:
如图2,分别延长AC、BF交于点G.
,,
,
,
,,
,
,
≌,
.
平分,
,
,
,
≌.
,
,
即.
【解析】根据尺规作图作BE平分,分别交AC,AD于点E,I即可;
在的条件下,根据角平分线的性质即可证明点I在的平分线上;
根据,,过点B作,垂足为点F,画出符合条件的图形,即可猜想BF和AD的数量关系.
本题考查了作图复杂作图、全等三角形的判定和性质、等腰三角形的判定和性质、角平分线的性质,解决本题的关键是准确画图.
18.【答案】解:;72;
证明:,
,
,
,
,
在与中,
,
≌,
,
是等腰三角形;
,
理由:由知,,
,
,
,
【解析】解:,
,
,
,
,
,
,
,
,
,;
故答案为:36;72;
见答案;
根据等腰三角形的性质得到,根据三角形的内角和即可得到结论;
根据已知条件得到,根据垂直的定义得到,根据全等三角形的性质即可得到结论;
由知,,根据线段的和差和等量代换即可得到结论.
本题考查了等腰三角形的判定与性质,全等三角形的判定与性质,熟练掌握等腰三角形的判定与性质是解题的关键.
第2页,共2页
第1页,共1页
考点一、等腰三角形的边与角的计算
如果等腰三角形的两边长分别为3和7,那么它的周长为______。
等腰三角形的一个内角为,则顶角的度数是______.
已知等腰三角形中有一个内角为,则该等腰三角形的底角为______.
已知等腰三角形的一个外角为,则它的顶角的度数为______.
一个等腰三角形的两边长分别为5和6,则这个等腰三角形的周长是 .
已知等腰三角形一腰上的高与另一腰的夹角为,则这个等腰三角形顶角的度数为______.
考点二、等腰三角形的性质
如图,在等腰三角形ABC中,,AD是边BC上的高,E是AD上一点.
求证:是等腰三角形;
若,,E是AD的中点,求的周长.
如图,已知D是等腰三角形ABC底边BC上一点,它到两腰AB,AC的距离分别为DE,DF.
当点D在什么位置时,?并加以证明.
探索DE,DF与等腰三角形ABC的高的关系.说明理由.
我们知道,经过三角形一顶点和此顶点所对边上的任意一点的直线,均能把三角形分割成两个三角形
如图,在中,,过B作一直线交AC于D,若BD把分割成两个等腰三角形,则的度数是________.
已知在中,,过顶点和顶点对边上一点的直线,把分割成两个等腰三角形,则的最小度数为________.
如图,为等腰三角形,,和分别为等边三角形,AE与BD相交于点F,连接CF交AB于点G,求证:G为AB的中点.
如图,在中,,D是BC的中点,于点E,于点F.
求证:;
如果,,求DE的长.
如图,中,,点E,F在边BC上,,点D在AF的延长线上,.
求证:≌;
若,则________.
考点三、等腰三角形的判定
如图,AD平分,,垂足为点D,.
求证:是等腰三角形.
已知:如图,中,,于D,BE平分,且于E,与CD相交于点F,H是BC边的中点,连结DH与BE相交于点G.
求证:;
求证:.
如图,在中,,,BD是的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF,求证:
;
为等腰三角形.
如图,CD是的高,,的平分线CE交AB于点E,设
求的度数用含的代数式表示;
求证:;
将沿直线BC折叠得到,连接AF、EF,若,求证:.
如图,在中,AD平分,交BC于点D.
尺规作图:作BE平分,分别交AC,AD于点E,I;
保留作图痕迹,不必写出作法
在的条件下,求证:点I在的平分线上;
若,,过点B作,垂足为点F,请画出符合条件的图形,猜想BF和AD的数量关系,并证明你的结论.
如图,在中,,D在边AC上,且.
如图1,填空______,______
如图2,若M为线段AC上的点,过M作直线于H,分别交直线AB、BC与点N、E.
求证:是等腰三角形;
试写出线段AN、CE、CD之间的数量关系,并加以证明.
答案和解析
1.【答案】17
【解析】
【分析】
题目给出等腰三角形有两条边长为3和7,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形。
【解答】
解:分两种情况讨论:
若3为腰长,7为底边长,
由于,则三角形不存在;
若7为腰长,则符合三角形的两边之和大于第三边,两边之差小于第三边。
所以这个三角形的周长为:。
故答案为17。
2.【答案】
【解析】解:,
的角是顶角,
故答案为:.
根据角是钝角判断出只能是顶角,然后根据等腰三角形两底角相等解答.
本题考查了等腰三角形两底角相等的性质,先判断出的角是顶角是解题的关键.
3.【答案】或
【解析】
【分析】
本题考查的是等腰三角形的性质及三角形内角和定理;解答此题时要注意的角是顶角和底角两种情况,不要漏解,分类讨论是正确解答本题的关键.由于不明确的角是等腰三角形的底角还是顶角,故应分的角是顶角和底角两种情况讨论.
【解答】
解:分两种情况:
当的角为等腰三角形的顶角时,
底角的度数;
当的角为等腰三角形的底角时,其底角为,
故它的底角度数是或.
故答案为或
4.【答案】或
【解析】解:当为顶角时,其他两角都为、,
当为底角时,其他两角为、,
所以等腰三角形的顶角为或.
故答案为:或.
等腰三角形的一个外角等于,则等腰三角形的一个内角为,但已知没有明确此角是顶角还是底角,所以应分两种情况进行分类讨论.
本题考查了等腰三角形的性质,及三角形内角和定理.
5.【答案】16或17
【解析】
【分析】
本题考查了等腰三角形的性质和三角形的三边关系.
由于未说明两边哪个是腰哪个是底,故需分:当等腰三角形的腰为当等腰三角形的腰为两种情况讨论,从而得到其周长.
【解答】
解:当等腰三角形的腰为5,底为6时,周长为;
当等腰三角形的腰为6,底为5时,周长为;
故这个等腰三角形的周长是16或17.
故答案为:16或17.
6.【答案】或
【解析】解:如图,
,,
,
,
;
如图,
,,
,
,
,
;
综上所述,它的顶角度数为:或.
故答案为:或.
分别从是锐角三角形与钝角三角形去分析求解即可求得答案.
此题考查了等腰三角形的性质.此题难度适中,注意掌握分类讨论思想的应用是解此题的关键.
7.【答案】在等腰三角形ABC中,,AD是边BC上的高,
.
垂直平分BC,
,即是等腰三角形;
是等腰三角形ABC的底边上的高,,
.
,
,
是AD的中点,
,
,
的周长是.
【解析】本题考查了等腰三角形的判定与性质、勾股定理及线段的垂直平分线的判定与性质,熟练掌握各定理的应用是解题关键.
根据等腰三角形的性质得到,根据线段垂直平分的性质得到,即可得证;
根据等腰三角形的性质得到CD的长,根据勾股定理得到AD的长,再根据勾股定理得到BE的长,即可得到的周长.
8.【答案】解:为中点时,,
理由是:如图,连接AD,
,D为BC中点,
平分,
,,
.
的长为腰上的高的长,
理由是:连接AD,过C作于M,
,
,
,
,
即的长为腰上的高的长.
【解析】本题考查了角平分线性质,等腰三角形性质,三角形面积的应用,题目具有一定的代表性,难度适中.
连接AD,根据三线合一定理求出AD平分,根据角平分线性质求出即可.
连接AD,过C作于M,根据三角形面积公式求出即可.
9.【答案】;
.
【解析】
【试题解析】
【分析】
本题主要考查等腰三角形的性质,三角形的内角和定理,注意分类讨论.
由可得,再根据三角形的内角和解答即可;
可分四种情况,利用等腰三角形的性质及三角形的内角和定理分别计算,即可求解的最小值.
【解答】
解:根据题意得,
,
.
故答案为;
如图1,,当,,
,
,
,
.
如图2,,,,
,,
,
,
,
,
.
如图3,,,
,,,
,
,
,
,
.
如图4,,,,
,,,
,
,
,
,
.
综上所述,的最小度数为.
10.【答案】证明:,
,
和为等边三角形,
,
,
.
在和中,
≌,
,
即CF平分,
又,
,
即G为AB的中点.
【解析】本题考查了全等三角形的判定与性质、等边三角形的性质以及等腰三角形三线合一的性质,证明三角形全等是解题的关键.
证明≌,可得,根据等腰三角形的性质即可解题.
11.【答案】解:证明:连接AD,如图,
,点D是BC边上的中点,
平分,
、DF分别垂直AB、AC于点E和F,
,点D是BC边上的中点,,
,
,
.
【解析】本题考查的是等腰三角形的性质、角平分线的性质、三角形的面积解题关键在于熟知等腰三角形三线合一的性质.
根据等腰三角形三线合一的特性,可得出AD也是的角平分线,根据角平分线的点到角两边的距离相等的性质即可得出答案
根据三角形中线的性质和三角形的面积解答即可得出答案.
12.【答案】解:,
,
在和中,
,
≌;
.
【解析】
【分析】
本题考查全等三角形的判定与性质,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
要证明≌,由题意可得,,,从而可以证明结论成立;
根据中的结论和等腰三角形的性质可以求得的度数.
【解答】
解:见答案;
≌,,
,
,
,
,
故答案为75.
13.【答案】证明:,
,
平分,
,
,
,
,,
,
,
是等腰三角形.
【解析】直接利用平行线的性质得出,进而利用角平分线的定义结合互余的性质得出,即可得出答案.
此题主要考查了平行线的性质以及角平分线的定义,正确得出是解题关键.
14.【答案】证明:,,
是等腰直角三角形.
.
,,且,
.
在和中,
,
≌,
.
证明:平分,
.
在和中,
,
≌.
,
又,
.
【解析】本题考查了三角形的内角和定理,等腰三角形的性质和判定,全等三角形的性质和判定的应用,关键是推出≌和≌,题目综合性比较强.
根据三角形的内角和定理求出,推出,根据AAS证出≌即可;
推出,,根据ASA证出≌,推出即可.
15.【答案】证明:,,
,
又是的平分线,
,
,
,
又是AB的中点,
,即;
,,
垂直平分AB,
,
,
又,
,
又,
,
,
,即为等腰三角形.
【解析】依据,,可得,再根据BD是的平分线,即可得到,由,可得,依据E是AB的中点,即可得到;
依据,,可得FE垂直平分AB,进而得出,依据,即可得到,再根据,可得,进而得到.
本题考查了等腰三角形的判定与性质,解决问题的关键是综合运用等腰三角形的判定与性质,线段垂直平分线的判定与性质,三角形外角的性质.
16.【答案】解:,,
,
平分,
,
是高,
,
.
证明:如图,在AD上截取,连接CH,
,
,
,,
,
,
,
;
如图,设EF交BC于点O,
,
,,
折叠的对称性,且E点的对称点为F点,
,,,
,
,解得,
由得,
,
,
,
,
,,
在中,,
由得,
.
【解析】本题考查三角形的内角和定理,角平分线的定义,平行线的性质,等腰三角形的判定和性质,折叠与对称,关键是掌握三角形的内角和定理,等腰三角形的判定和性质,轴对称的性质,正确应用有关性质即可解答.
根据角平分线的定义,三角形的内角和定理用含有的代数式分别表示、、、即可解答;
在AD上截取,连接CH,先根据等腰三角形的性质用含有的代数式分别表示、、、、得,再根据等腰三角形的判定和性质即可解答;
设EF交BC于点O,先根据平分线的性质得,,再根据轴对称的性质得,,,最后根据,得关于的方程,解方程求得的值即可求解得证.
17.【答案】如图1,线段BE就是所求作的角平分线;
证明:
如图1,过点I作,,,点F,G,H为垂足.
平分,,,
.
同理可得:.
,
,,
点I在的平分线上角的内部到角两边距离相等的点在角的平分线上.
和AD的数量关系是:或
证明如下:
如图2,分别延长AC、BF交于点G.
,,
,
,
,,
,
,
≌,
.
平分,
,
,
,
≌.
,
,
即.
【解析】根据尺规作图作BE平分,分别交AC,AD于点E,I即可;
在的条件下,根据角平分线的性质即可证明点I在的平分线上;
根据,,过点B作,垂足为点F,画出符合条件的图形,即可猜想BF和AD的数量关系.
本题考查了作图复杂作图、全等三角形的判定和性质、等腰三角形的判定和性质、角平分线的性质,解决本题的关键是准确画图.
18.【答案】解:;72;
证明:,
,
,
,
,
在与中,
,
≌,
,
是等腰三角形;
,
理由:由知,,
,
,
,
【解析】解:,
,
,
,
,
,
,
,
,
,;
故答案为:36;72;
见答案;
根据等腰三角形的性质得到,根据三角形的内角和即可得到结论;
根据已知条件得到,根据垂直的定义得到,根据全等三角形的性质即可得到结论;
由知,,根据线段的和差和等量代换即可得到结论.
本题考查了等腰三角形的判定与性质,全等三角形的判定与性质,熟练掌握等腰三角形的判定与性质是解题的关键.
第2页,共2页
第1页,共1页
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
