2021-2022学年北师大版九年级数学上册4.4探索三角形相似的条件课后小练(Word版,附答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册4.4探索三角形相似的条件课后小练(Word版,附答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 772.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-16 21:33:00 | ||
图片预览



文档简介
2021-2022学年数学北师大版九年级上册图形的相似
课后小练(4)探索三角形相似的条件
1.已知,若,,则与的相似比为( )
A. B. C. D.
2.如图,在与中,,要使与相似,还需满足下列条件中的( )
A. B. C. D.
3.如图,在中,E为BC中点,连接AE交对角线BD于F,若,则FD等于( )
A.2 B.3 C.4 D.6
4.如图,在中,,将绕点B逆时针旋转得到,点E在AC上,若,,则( )
A. B. C. D.2
5.如图,有左、右并排的两棵树AB和CD,小树AB的高m,大树CD的高m,小明估计自己眼睛距地面的高度m,当他站在F点时恰好看到大树顶端C点.已知此时他与小树的距离m,则两棵树之间的距离BD是( )
A.1 m B. m C.3 m D. m
6.如图,在中,,且,则的值为( )
A. B. C. D.
7.如图,在中,点E,F分别在边AD,BC上,且,G为边AD延长线上的一点,连接BG,分别交DC,EF于M,N,则图中与相似的三角形有( )
A.1个 B.2个 C.3个 D.4个
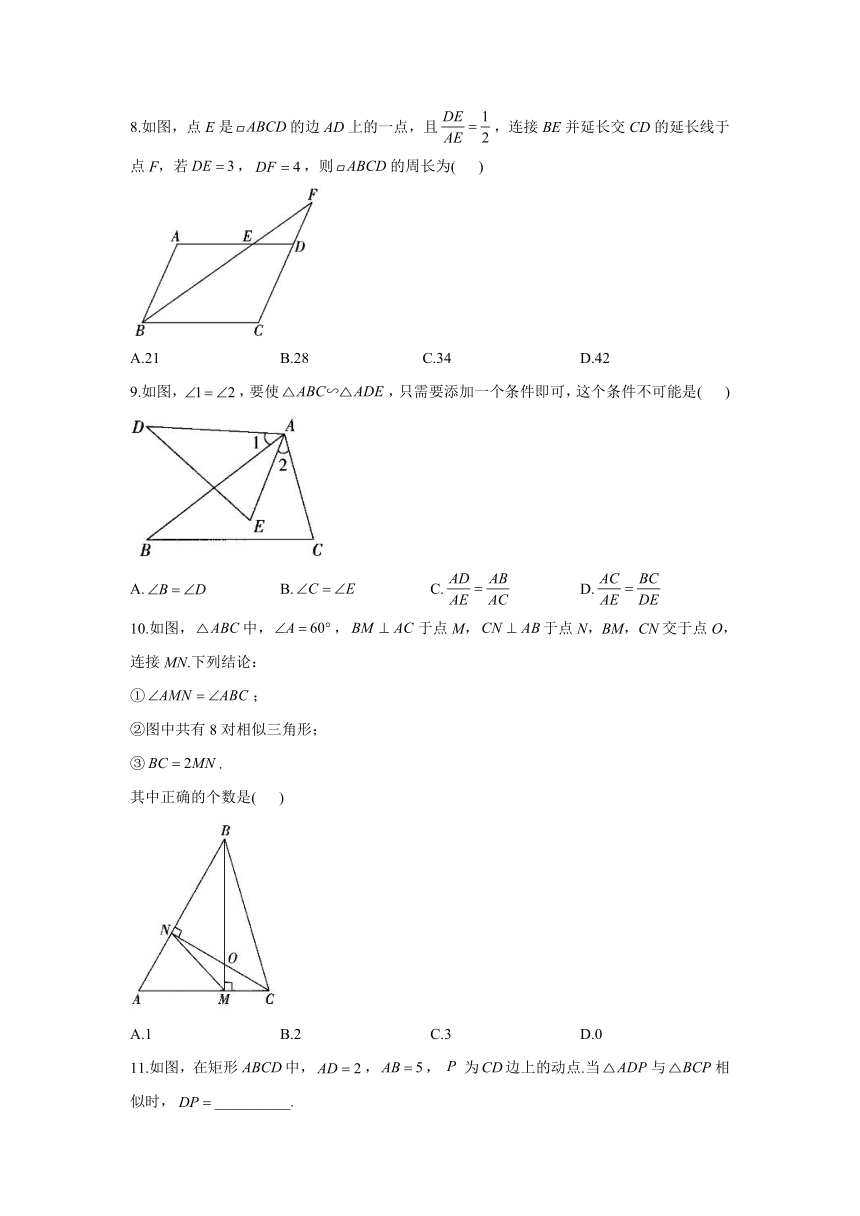
8.如图,点E是的边AD上的一点,且,连接BE并延长交CD的延长线于点F,若,,则的周长为( )
A.21 B.28 C.34 D.42
9.如图,,要使,只需要添加一个条件即可,这个条件不可能是( )
A. B. C. D.
10.如图,中,,于点M,于点N,BM,CN交于点O,连接MN.下列结论:
①;
②图中共有8对相似三角形;
③.
其中正确的个数是( )
A.1 B.2 C.3 D.0
11.如图,在矩形中,,,为边上的动点.当与相似时,__________.
12.如图,在中,,,点D是AB的中点,连接CD,点E是AC上一点,且,点F是CD的中点,连接EF,则EF的长为_____________.
13.如图,在中, m, m,点P从B点出发,沿BC方向以2m/s的速度移动,点Q从C出发,沿CA方向以1m/s的速度移动.若P、Q同时分别从B、C出发,经过_____________s,.
14.和满足下列条件:
①;
②;
③;
④
其中能判定和相似的有__________.
15.如图,在平行四边形ABCD中,连接对角线AC,延长AB至点E,使,连接DE,分别交BC,AC于点F,G.
(1)求证:;
(2)若,求FG的长.
答案以及解析
1.答案:D
解析:对应边的比等于相似比,且有顺序性,故与的相似比为.故选D.
2.答案:C
解析:故选C.
3.答案:C
解析:在中,E为BC中点,,,,,即,.故选C.
4.答案:A
解析:由旋转可得,,,.又,,又,,,即,,.故选A.
5.答案:B
解析:由题意,得m, m, m,m,,,,,,,即,解得m,则m.故选B.
6.答案:A
解析:,.,.故选A.
7.答案:D
解析:四边形ABCD为平行四边形,,,,,,,,.故选D.
8.答案:C
解析:四边形ABCD是平行四边形,,,.,,,,,
的周长.故选C.
9.答案:D
解析:,,.选项A,添加,利用“两角定理”可得,故A不合题意;选项B,添加,利用“两角定理”可得,故B不合题意;选项C,添加(即),利用“两边夹角定理”可得,故C不合题意;选项D,添加,不能证明,故D符合题意.故选D.
10.答案:C
解析:,,,又,,,即,又,,,故①正确;易得,,,图中共有8对相似三角形,故②正确;中,,,,,,即,故③正确.故选C.
11.答案:1或4或2.5
解析:①当时,,即,解得或.
②当时,,即,解得.综上所述,的长度是1或4或2.5.
12.答案:
解析:连接ED.是等腰直角三角形,点D是AB的中点,,.,,,.又,,,,是直角三角形,又点F为CD的中点,.
13.答案:2.4
解析:设经过t s,,在中,, m, m,由勾股定理得(m).,,即..
14.答案:①②③
解析:①根据三角形内角和定理得到,则在和中,,所以和相似.故①正确.②根据题意知,所以和相似.故②正确.③根据题意知.所以和相似.故③正确.④当时,和才相似.故④不正确.综上所述,能判定和相似的有①②③.
15.答案:(1)证明:四边形ABCD是平行四边形,
,,
,
,
,.
(2)四边形ABCD是平行四边形,
,,
,即,
解得.
课后小练(4)探索三角形相似的条件
1.已知,若,,则与的相似比为( )
A. B. C. D.
2.如图,在与中,,要使与相似,还需满足下列条件中的( )
A. B. C. D.
3.如图,在中,E为BC中点,连接AE交对角线BD于F,若,则FD等于( )
A.2 B.3 C.4 D.6
4.如图,在中,,将绕点B逆时针旋转得到,点E在AC上,若,,则( )
A. B. C. D.2
5.如图,有左、右并排的两棵树AB和CD,小树AB的高m,大树CD的高m,小明估计自己眼睛距地面的高度m,当他站在F点时恰好看到大树顶端C点.已知此时他与小树的距离m,则两棵树之间的距离BD是( )
A.1 m B. m C.3 m D. m
6.如图,在中,,且,则的值为( )
A. B. C. D.
7.如图,在中,点E,F分别在边AD,BC上,且,G为边AD延长线上的一点,连接BG,分别交DC,EF于M,N,则图中与相似的三角形有( )
A.1个 B.2个 C.3个 D.4个
8.如图,点E是的边AD上的一点,且,连接BE并延长交CD的延长线于点F,若,,则的周长为( )
A.21 B.28 C.34 D.42
9.如图,,要使,只需要添加一个条件即可,这个条件不可能是( )
A. B. C. D.
10.如图,中,,于点M,于点N,BM,CN交于点O,连接MN.下列结论:
①;
②图中共有8对相似三角形;
③.
其中正确的个数是( )
A.1 B.2 C.3 D.0
11.如图,在矩形中,,,为边上的动点.当与相似时,__________.
12.如图,在中,,,点D是AB的中点,连接CD,点E是AC上一点,且,点F是CD的中点,连接EF,则EF的长为_____________.
13.如图,在中, m, m,点P从B点出发,沿BC方向以2m/s的速度移动,点Q从C出发,沿CA方向以1m/s的速度移动.若P、Q同时分别从B、C出发,经过_____________s,.
14.和满足下列条件:
①;
②;
③;
④
其中能判定和相似的有__________.
15.如图,在平行四边形ABCD中,连接对角线AC,延长AB至点E,使,连接DE,分别交BC,AC于点F,G.
(1)求证:;
(2)若,求FG的长.
答案以及解析
1.答案:D
解析:对应边的比等于相似比,且有顺序性,故与的相似比为.故选D.
2.答案:C
解析:故选C.
3.答案:C
解析:在中,E为BC中点,,,,,即,.故选C.
4.答案:A
解析:由旋转可得,,,.又,,又,,,即,,.故选A.
5.答案:B
解析:由题意,得m, m, m,m,,,,,,,即,解得m,则m.故选B.
6.答案:A
解析:,.,.故选A.
7.答案:D
解析:四边形ABCD为平行四边形,,,,,,,,.故选D.
8.答案:C
解析:四边形ABCD是平行四边形,,,.,,,,,
的周长.故选C.
9.答案:D
解析:,,.选项A,添加,利用“两角定理”可得,故A不合题意;选项B,添加,利用“两角定理”可得,故B不合题意;选项C,添加(即),利用“两边夹角定理”可得,故C不合题意;选项D,添加,不能证明,故D符合题意.故选D.
10.答案:C
解析:,,,又,,,即,又,,,故①正确;易得,,,图中共有8对相似三角形,故②正确;中,,,,,,即,故③正确.故选C.
11.答案:1或4或2.5
解析:①当时,,即,解得或.
②当时,,即,解得.综上所述,的长度是1或4或2.5.
12.答案:
解析:连接ED.是等腰直角三角形,点D是AB的中点,,.,,,.又,,,,是直角三角形,又点F为CD的中点,.
13.答案:2.4
解析:设经过t s,,在中,, m, m,由勾股定理得(m).,,即..
14.答案:①②③
解析:①根据三角形内角和定理得到,则在和中,,所以和相似.故①正确.②根据题意知,所以和相似.故②正确.③根据题意知.所以和相似.故③正确.④当时,和才相似.故④不正确.综上所述,能判定和相似的有①②③.
15.答案:(1)证明:四边形ABCD是平行四边形,
,,
,
,
,.
(2)四边形ABCD是平行四边形,
,,
,即,
解得.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
