2021-2022学年北师大版七年级数学上册 第2章整式及其加减 知识点分类训练 (word版含解析)
文档属性
| 名称 | 2021-2022学年北师大版七年级数学上册 第2章整式及其加减 知识点分类训练 (word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 297.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-16 12:58:38 | ||
图片预览




文档简介
2021-2022学年北师大版七年级数学上册《第2章整式的加减》知识点分类训练(附答案)
一.代数式
1.下列各式中,符合代数式书写规则的是( )
A. B. C. D.2y÷z
2.下列各式符合代数式书写规范的是( )
A. B.a×3 C.2m﹣1个 D.
3.下列各式:ab 2,m÷2n,xy,1a,其中符合代数式书写规范的有 个.
二.列代数式
4.某商品标价x元,进价为400元,在商场开展的促销活动中,该商品按8折销售获利( )
A.(8x﹣400)元 B.(400×8﹣x)元
C.(0.8x﹣400)元 D.(400×0.8﹣x)元
5.用式子表示“a的2倍与b的差的平方”,正确的是( )
A.2(a﹣b)2 B.2a﹣b2 C.(a﹣2b)2 D.(2a﹣b)2
6.如图是一块长为a,宽为b(a>b)的长方形空地,要将阴影部分绿化,则阴影面积是( )
A.a2b2 B.ab﹣πa2 C. D.
7.如图,长方形纸片上画有两个完全相同的阴影长方形,那么剩余的非阴影长方形的周长为 (用含a,b的代数式表示).
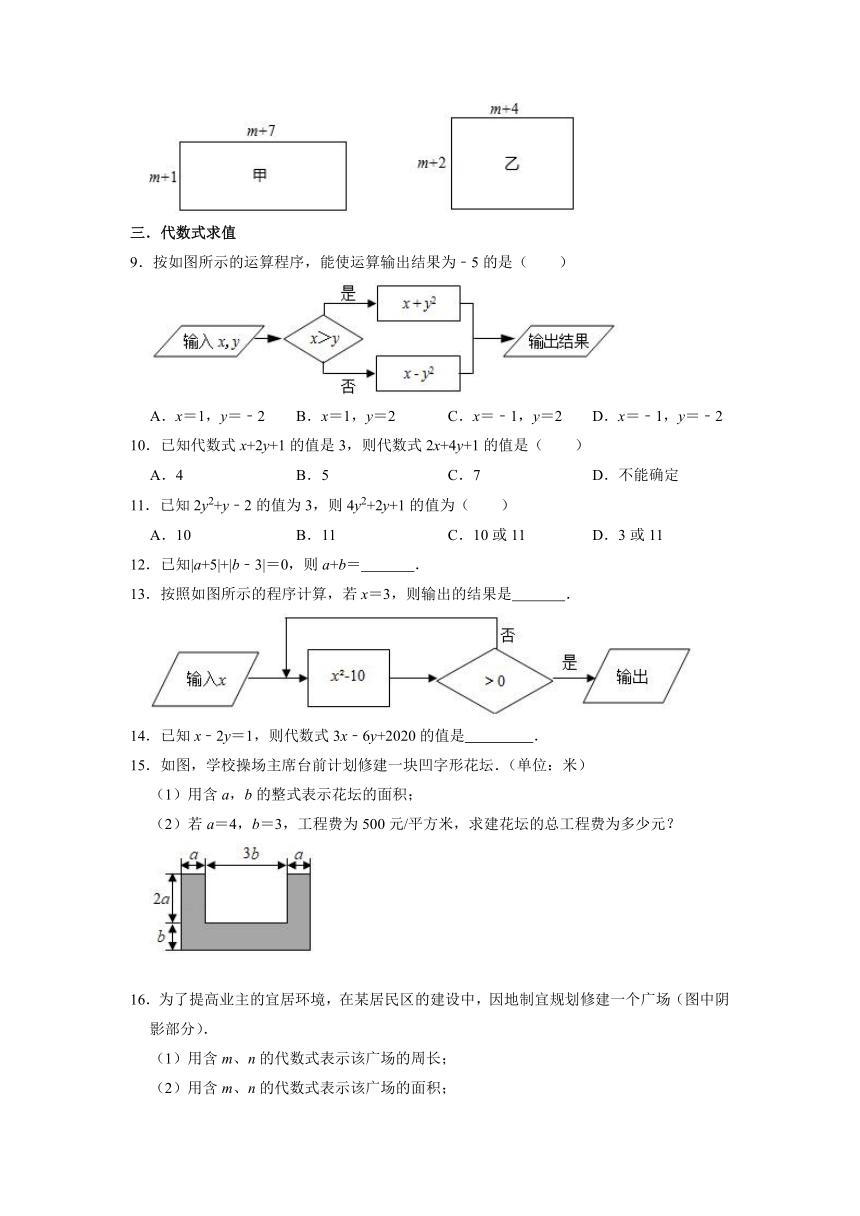
8.如图,甲、乙都是长方形,边长的数据如图所示(其中m为正整数).
(1)用含m的代数式表示:图中的甲长方形的面积S1= ,乙长方形的面积S2= ;
(2)请你先判断S1与S2的大小关系,并说明理由;
(3)现有一正方形,其周长与图中的甲长方形周长相等,试探究:该正方形面积S与图中的甲长方形面积S1的差(即S﹣S1)是一个常数,求出这个常数.
三.代数式求值
9.按如图所示的运算程序,能使运算输出结果为﹣5的是( )
A.x=1,y=﹣2 B.x=1,y=2 C.x=﹣1,y=2 D.x=﹣1,y=﹣2
10.已知代数式x+2y+1的值是3,则代数式2x+4y+1的值是( )
A.4 B.5 C.7 D.不能确定
11.已知2y2+y﹣2的值为3,则4y2+2y+1的值为( )
A.10 B.11 C.10或11 D.3或11
12.已知|a+5|+|b﹣3|=0,则a+b= .
13.按照如图所示的程序计算,若x=3,则输出的结果是 .
14.已知x﹣2y=1,则代数式3x﹣6y+2020的值是 .
15.如图,学校操场主席台前计划修建一块凹字形花坛.(单位:米)
(1)用含a,b的整式表示花坛的面积;
(2)若a=4,b=3,工程费为500元/平方米,求建花坛的总工程费为多少元?
16.为了提高业主的宜居环境,在某居民区的建设中,因地制宜规划修建一个广场(图中阴影部分).
(1)用含m、n的代数式表示该广场的周长;
(2)用含m、n的代数式表示该广场的面积;
(3)当m=6,n=8时,求出该广场的周长和面积.
四.同类项
17.已知﹣5xay与2x2yb为同类项,则a﹣b的值为( )
A.1 B.2 C.3 D.4
18.下列各式中,是5x2y的同类项的是( )
A.x2y B.﹣3x2yz C.3a2b D.5x3
19.若a2n+1b2与﹣5b2a3n﹣2是同类项,则n= .
五.合并同类项
20.下列运算正确的是( )
A.3a+2a=5a2 B.3a+3b=3ab
C.a5﹣a2=a3 D.2a2b﹣a2b=a2b
21.下列计算正确的是( )
A.﹣a2﹣a2=﹣2a2 B.3a2+a=4a2
C.4a﹣2a=2 D.2a2﹣a=a
22.下列各式中,正确的是( )
A.x2y﹣2x2y=﹣x2y B.2a+3b=5ab
C.7ab﹣3ab=4 D.a3+a2=a5
23.若2xm﹣3y5与﹣3x2yn+2的和是单项式,则m+n= .
24.合并同类项:5m+2n﹣m﹣3n.
六.去括号与添括号
25.下列变形正确的是( )
A.﹣(a+2)=a﹣2 B.﹣(2a﹣1)=﹣2a+1
C.﹣a+1=﹣(a﹣1) D.1﹣a=﹣(a+1)
26.下列去括号正确的是( )
A.﹣3(b﹣1)=﹣3b+1 B.﹣3(a﹣2)=﹣3a﹣6
C.﹣3(b﹣1)=3﹣3b D.﹣3(a﹣2)=3a﹣6
27.下列去括号中,正确的是( )
A.a2﹣(2a﹣1)=a2﹣2a﹣1
B.a2+(﹣2a﹣3)=a2﹣2a+3
C.3a﹣[5b﹣(2c﹣1)]=3a﹣5b+2c﹣1
D.﹣(a+b)+(c﹣d)=﹣a﹣b﹣c+d
28.下列各式,去括号正确的是( )
A.a+(b﹣c)+d=a﹣b+c﹣d B.a﹣(b﹣c+d)=a﹣b﹣c+d
C.a﹣(b﹣c+d)=a﹣b+c﹣d D.a﹣(b﹣c+d)=a﹣b+c+d
七.规律型:数字的变化类
29.将一列有理数﹣1,2,﹣3,4,﹣5,6,…,按如图所示进行排列,则﹣2021应排在( )
A.A位置 B.B位置 C.D位置 D.E位置
30.小刚在做数学题时,发现下面有趣的结果:
第1行:3﹣2=1
第2行:8+7﹣6﹣5=4
第3行:15+14+13﹣12﹣11﹣10=9
第4行:24+23+22+21﹣20﹣19﹣18﹣17=16
……
根据以上规律,“2021”在第m行,从左往右数第n个,那么m+n= .
31.如图是一根起点为1的数轴,现有同学将它弯折,弯折后虚线上由左至右第1个数是1,第2个数是13,第3个数是41,…,依此规律,第7个数是 .
32.观察下列式子,
①=1﹣,
②=﹣,
③=﹣,
…
(1)用正整数n表示这个规律 ;
(2)设F(n)=++…+,解决下列问题:
①F(10)= ;
②问:F(1)+++…+与F(n)相等吗?并说明理由.
八.整式
33.下列说法中,不正确的是( )
A.﹣ab2c的系数是﹣1,次数是4
B.﹣1是整式
C.6x2﹣3x+1的项是6x2、﹣3x,1
D.2πR+πR2是三次二项式
34.下列说法中正确的是( )
A.不是整式 B.﹣3x3y的次数是4
C.4ab与4xy是同类项 D.是单项式
九.单项式
35.在代数式:a,m+6,﹣5,a2b﹣2ab,3mn,中,单项式有( )
A.2个 B.3个 C.4个 D.5个
36.单项式﹣的系数是 ,次数是 .
37.单项式﹣的系数是 ,次数是 .
十.多项式
38.下列说法中,正确的是( )
A.单项式xy2的系数是x
B.单项式﹣5x2的次数为﹣5
C.多项式x2+2x+18是二次三项式
D.多项式x2+y2﹣1的常数项是1
39.要使多项式6x+5y﹣3+2ky+4k不含y的项,则k的值是( )
A.0 B. C. D.﹣
40.多项式3是( )
A.三次四项式 B.三次三项式 C.四次四项式 D.二次四项式
41.多项式ab2﹣5ab+2b﹣1的次数是 ,常数项是 .
42.当m= 时,多项式x2﹣mxy﹣3y2中不含xy项.
43.若关于x的多项式2x3+2mx2﹣5x﹣8x2﹣1不含二次项,则m= .
44.多项式﹣a3b﹣7ab﹣6ab4+1是 次 项式,它最高项的系数是 .
45.如果x+y=3,xy=2,则多项式x2y+xy2的值为 .
46.下列代数式中的哪些是单项式,哪些是多项式,哪些是整式?
,4xy,,,x2+x+,0,,m,﹣2.01×105
整式集合:{ …}
单项式集合:{ …}
多项式集合:{ …}.
47.已知代数式3xn﹣(m﹣1)x+1是关于x的三次二项式,求m、n的条件.
十一.整式的加减
48.若关于a,b的多项式3(a2﹣2ab﹣b2)﹣(a2+mab+2b2)中不含有ab项,则m= .
49.多项式8x2﹣3x+5与3x3+2mx2﹣5x+7相加后不含x的二次项,则常数m的值等于 .
50.化简
(1)3m+2n﹣5m﹣n;
(2)(5a﹣3b)﹣3(a﹣2b).
51.在整式的加减运算练习课上,小明同学将“2A﹣B”看成“A﹣2B”,算得错误结果是4a2b﹣3ab2+4abc,已知A=6a2b﹣ab2+2abc.请你解决以下问题:
(1)求出整式B;
(2)求出2A﹣B;
(3)若增加条件:a,b满足|a﹣2|+(b+1)2=0,你能求出(2)中代数式的值吗?如果能,请求出最后的值;如果不能,请说明理由.
52.化简:
(1)(4x2y﹣6xy2)﹣(3xy2﹣5x2y);
(2)2(2x﹣7y)﹣3(3x﹣10y).
53.化简:
(1)5m﹣7n﹣8p+5n﹣9m﹣p; (2)x+2(3y2﹣2x)﹣4(2x﹣y2).
54.化简:
(1)﹣2x﹣3+4x﹣x; (2)(2a2+a﹣1)﹣(2﹣3a+2a2).
55.如图,一个大长方形中剪下两个大小相同的小长方形(有关线段的长如图所示)留下一个“T”型的图形(阴影部分).
(1)用含x,y的代数式表示阴影部分的周长;
(2)用含x,y的代数式表示阴影部分的面积;
(3)当x=2,y=2.5时,计算阴影部分的面积.
56.化简:
(1)(﹣4x2+2x﹣8)﹣2(x﹣1)
(2)2(x2y+xy2)﹣2(x2y﹣3x)﹣2xy2﹣2y
十二.整式的加减—化简求值
57.先化简,后求值:a2﹣(3a2﹣2b2)+3(a2﹣b2),其中a=﹣3,b=﹣2.
58.解下列各题:
(1)化简:﹣5a+(3a﹣2)+(7﹣3a);
(2)先化简,再求值:3a2b﹣ab2﹣(﹣ab2+2a2b﹣1)其中a=﹣2,b=3.
59.化简、求值:
(1)先化简、再求值:(a+6a2)+3(a﹣2a2),其中a=1;
(2)化简:已知A=a2﹣2ab+b2,B=a2+2ab+b2,求(B﹣A).
60.先化简,再求值:4(x﹣1)﹣2(x2+1)+(4x2﹣2x),其中x=﹣2.
参考答案
一.代数式
1.解:A、符合代数式书写规则.
B、不符合代数式书写规则,应该为.
C、不符合代数式书写规则,应该为﹣.
D、不符合代数式书写规则,应改为.
故选:A.
2.解:A、除法按照分数的写法来写,原书写规范,故A符合题意;
B、数字与字母相乘时,数字要写在字母的前面且省略乘号,原书写不规范,故B不符合题意;
C、代数和后面写单位要加括号,原书写不规范,故C不符合题意;
D、带分数要写成假分数的形式,原书写不规范,故D不符合题意;
故选:A.
3.解:在ab 2,m÷2n,xy,1a,中,符合代数式书写规范的有xy,,共2个;
故答案为:2.
二.列代数式
4.解:由题意可得,
该商品按8折销售获利为:(0.8x﹣400)元,
故选:C.
5.解:a的2倍为2a,与b的差的平方为(2a﹣b)2
故选:D.
6.解:由图可得,
阴影部分的面积是:ab﹣=,
故选:C.
7.解:由题意可得,非阴影长方形的周长为:2(b﹣a)+2b=4b﹣2a.
故答案为:4b﹣2a.
8.解:(1)S1=(m+1)(m+7)=m2+8m+7,
S2=(m+2)(m+4)=m2+6m+8.
故答案为:m2+8m+7,m2+6m+8;
(2)S1>S2,理由如下:
S1﹣S2=(m2+8m+7)﹣(m2+6m+8)=2m﹣1,
∵m为正整数,
∴2m﹣1>0,
∴S1>S2;
(3)图中甲的长方形周长为2(m+7+m+1)=4m+16,
∴该正方形边长为m+4,
∴S﹣S1=(m+4)2﹣(m2+8m+7)=9,
∴这个常数为9.
三.代数式求值
9.解:A、当x=1,y=﹣2时,输出结果为1+4=5,不符合题意;
B、当x=1,y=2时,输出结果为1﹣4=﹣3,不符合题意;
C、当x=﹣1,y=2时,输出结果为﹣1﹣4=﹣5,符合题意;
D、当x=﹣1,y=﹣2时,输出结果为﹣1+4=3,不符合题意,
故选:C.
10.解:根据题意得
x+2y+1=3,
∴x+2y=2,
那么2x+4y+1=2(x+2y)+1=2×2+1=5.
故选:B.
11.解:∵2y2+y﹣2的值为3,
∴2y2+y﹣2=3,
∴2y2+y=5,
∴2(2y2+y)=4y2+2y=10,
∴4y2+2y+1=11.
故选:B.
12.解:由题意得a+5=0,b﹣3=0,
解得a=﹣5,b=3,
所以a+b=﹣5+3=﹣2.
故答案为:﹣2.
13.解:当x=3时,x2﹣10=9﹣10=﹣1<0,
于是再把x=﹣1输入,x2﹣10=1﹣10=﹣9<0,
再把x=﹣9输入,x2﹣10=81﹣10=71>0,
因此输出的数为:71,
故答案为:71.
14.解:∵x﹣2y=1,
∴3x﹣6y+2020
=3(x﹣2y)+2020
=3×1+2020
=3+2020
=2023.
故答案为:2023.
15.解:(1)(a+3b+a)(2a+b)﹣2a 3b
=4a2+8ab+3b2﹣6ab
=(4a2+2ab+3b2)(平方米).
答:花坛的面积是(4a2+2ab+3b2)平方米.
(2)当a=4,b=3时,
4a2+2ab+3b2
=4×42+4×2×3+3×32
=115(平方米),
115×500=57500(元).
答:建花坛的总工程费为57500元.
16.解:(1)C=6m+4n;
(2)S=2m×2n﹣m(2n﹣n﹣0.5n)
=4mn﹣0.5mn
=3.5mn;
(3)把m=6,n=8,代入周长6m+4n=6×6+4×8=68,
把m=6,n=8,代入面积3.5mn=3.5×6×8=168.
四.同类项
17.解:∵﹣5xay与2x2yb是同类项,
∴a=2,b=1,
故a﹣b=2﹣1=1.
故选:A.
18.解:A.5x2y与x2y,所含的字母相同:x、y,它们的指数也相同,所以它们是同类项,故本选项符合题意;
B.5x2y与﹣3x2yz,所含的字母不相同,所以它们不是同类项,故本选项不合题意;
C.5x2y与3a2b,所含的字母不相同,所以它们不是同类项,故本选项不合题意;
D.5x2y与5x3,所含的字母不相同,所以它们不是同类项,故本选项不合题意.
故选:A.
19.解:∵a2n+1b2与﹣5b2a3n﹣2是同类项,
∴2n+1=3n﹣2,
解得:n=3.
故答案为:3.
五.合并同类项
20.解:A、3a+2a=5a,故本选项不合题意;
B、3a与3b不是同类项,所以不能合并,故本选项不合题意;
C、a5与﹣a2不是同类项,所以不能合并,故本选项不合题意;
D、2a2b﹣a2b=a2b,故本选项符合题意.
故选:D.
21.解:A、﹣a2﹣a2=﹣2a2=(﹣1﹣1)a2=﹣2a2,故A正确;
B、不是同类项不能合并,故B错误;
C、4a﹣2a=(4﹣2)a=2a,故C错误;
D、不是同类项不能合并,故D错误.
故选:A.
22.解:A、x2y﹣2x2y=﹣x2y,故A正确;
B、不是同类项,不能进一步计算,故B错误;
C、7ab﹣3ab=4ab,故C错误;
D、a3+a2=a5,不是同类项,故D错误.
故选:A.
23.解:∵2xm﹣3y5与﹣3x2yn+2的和是单项式,
∴2xm﹣3y5与﹣3x2yn+2是同类项,
∴m﹣3=2,n+2=5,
∴m=5,n=3,
∴m+n=5+3=8.
故答案为:8.
24.解:5m+2n﹣m﹣3n
=(5m﹣m)+(2n﹣3n)
=4m﹣n.
六.去括号与添括号
25.解:A、原式=﹣a﹣2,故本选项变形错误.
B、原式=﹣a+,故本选项变形错误.
C、原式=﹣(a﹣1),故本选项变形正确.
D、原式=﹣(a﹣1),故本选项变形错误.
故选:C.
26.解:A、﹣3(b﹣1)=﹣3b+3,故此选项错误;
B、﹣3(a﹣2)=﹣3a+6,故此选项错误;
C、﹣3(b﹣1)=3﹣3b,故此选项正确;
D、﹣3(a﹣2)=﹣3a+6,故此选项错误;
故选:C.
27.解:A,a2﹣(2a﹣1)=a2﹣2a+1,故此选项错误;
B,a2+(﹣2a﹣3)=a2﹣2a﹣3,故此选项错误;
C,3a﹣[5b﹣(2c﹣1)]=3a﹣5b+2c﹣1,故此选项正确;
D,﹣(a+b)+(c﹣d)=﹣a﹣b+c﹣d,故此选项错误;
故选:C.
28.解:A、a+(b﹣c)+d=a+b﹣c+d,故错误;
B、a﹣(b﹣c+d)=a﹣b+c﹣d,故错误;
D、a﹣(b﹣c+d)=a﹣b+c﹣d,故错误;
只有C符合运算方法,正确.
故选:C.
七.规律型:数字的变化类
29.解:由图可知,
每个凸起对应5个数字,这些数字的奇数都是负数,偶数都是正数,
∵(2021﹣1)÷5=2020÷5=404,
∴﹣2021应排在E位置,
故选:D.
30.解:∵(43+1)2﹣1=1935,
(44+1)2﹣1=2024,
∴2021这个数出现在第44行,左起第2024﹣2021+1=4个数.
∴m=44,n=4,
∴m+n=44+4=48,
故答案为48.
31.解:第二个数13=12+1=3×4+1,
第三个数41=40+1=5×8+1,
则第七个数=[5+(7﹣3)×2]×[8+(7﹣3)×4]+1=13×24+1=313.
故答案为:313.
32.解:(1)用正整数n表示这个规律为:,
等式右边=﹣===等式左边,
即等式成立,
故答案为:;
(2)①F(10)=++…+=1﹣++…+=1﹣=,
故答案为:;
②相等,理由如下:
F(1)+++…+=+++......+=+++......+=F(n),
即相等.
八.整式
33.解:A、﹣ab2c的系数是﹣1,次数是4,故A正确;
B、﹣1是整式,故B正确;
C、6x2﹣3x+1的项是6x2、﹣3x,1,故C正确;
D、2πR+πR2是二次二项式,故D错误;
故选:D.
34.解:A、是整式,故错误;
B、﹣3x3y的次数是4,正确;
C、4ab与4xy不是同类项,故错误;
D、不是单项式,是分式故错误.
故选:B.
九.单项式
35.解:代数式a,m+6,﹣5,a2b﹣2ab,3mn,中,单项式有:
a,﹣5,3mn,共有3个.
故选:B.
36.解:单项式﹣的系数是:﹣,
次数是:3.
故答案为:﹣,3.
37.解:单项式﹣的系数是﹣,次数是5;
故答案为:﹣;5.
十.多项式
38.解:A、单项式xy2的系数是,原说法错误,故此选项不符合题意;
B、单项式﹣5x2的次数为2,原说法错误,故此选项不符合题意;
C、多项式x2+2x+18是二次三项式,原说法正确,故此选项符合题意;
D、多项式x2+y2﹣1的常数项是﹣1,原说法错误,故此选项不符合题意,
故选:C.
39.解:要使多项式6x+5y﹣3+2ky+4k不含y的项,则y的系数应为0,
多项式6x+5y﹣3+2ky+4k中,5y和2ky两项含有y,要求这两项的系数互为相反数,
合并同类项时,
为2k+5=0,
即k=﹣.
故选:D.
40.解:因为多项式3的各项的次数分别为2,3,1,0,
由于多项式的次数是“多项式中次数最高的项的次数”,
所以多项式3的次数是3,
又因为它有四个单项式组成,所以它是三次四项式.
故选:A.
41.解:多项式ab2﹣5ab+2b﹣1的次数是3,常数项为﹣1,
故答案为:3,﹣1.
42.解:∵多项式x2﹣mxy﹣3y2中不含xy项,
∴﹣m+=0,
解得:m=.
故答案为:.
43.解:2x3+2mx2﹣5x﹣8x2﹣1=2x3+(2m﹣8)x2﹣5x﹣1,
∵关于x的多项式2x3+2mx2﹣5x﹣8x2﹣1不含二次项,
∴2m﹣8=0,
解得:m=4,
故答案为:4.
44.解:依题意得原式是一个五次四项式,它的最高项的系数是﹣6.
故填空答案:五,四,﹣6.
45.解:x2y+xy2=xy(x+y)=2×3=6.
46.解:整式集合:{,4xy,,0,m,﹣2.01×105 …};
单项式集合:{ 4xy,,0,m,﹣2.01×105 …};
多项式集合:{ …}.
故答案为:{,4xy,,0,m,﹣2.01×105 …};{ 4xy,,0,m,﹣2.01×105 …};{ …}.
47.解:∵代数式3xn﹣(m﹣1)x+1是关于x的三次二项式,
∴n=3,m﹣1=0,
解得:m=1,n=3.
十一.整式的加减
48.解:原式=3a2﹣6ab﹣3b2﹣a2﹣mab﹣2b2=2a2﹣(6+m)ab﹣5b2,
由于多项式中不含有ab项,
故﹣(6+m)=0,
∴m=﹣6,
故填空答案:﹣6.
49.解:∵多项式8x2﹣3x+5与3x3+2mx2﹣5x+7相加后不含x的二次项,
∴8x2+2mx2=(2m+8)x2,
∴2m+8=0,
解得m=﹣4.
故答案为﹣4.
50.解:(1)3m+2n﹣5m﹣n
=(3m﹣5m)+(2n﹣n)
=﹣2m+n;
(2)(5a﹣3b)﹣3(a﹣2b)
=5a﹣3b﹣3a+6b
=(5a﹣3a)+(﹣3b+6b)
=2a+3b.
51.解:(1)根据题意B=[(6a2b﹣ab2+2abc)﹣(4a2b﹣3ab2+4abc)]÷2
=(6a2b﹣ab2+2abc﹣4a2b+3ab2﹣4abc)÷2
=(2a2b﹣2abc+2ab2)÷2
=a2b﹣abc+ab2;
(2)2A﹣B
=2(6a2b﹣ab2+2abc)﹣(a2b﹣abc+ab2)
=12a2b﹣2ab2+4abc﹣a2b+abc﹣ab2
=11a2b+5abc﹣3ab2;
(3)∵|a﹣2|+(b+1)2=0,
∴a﹣2=0且b+1=0,
∴a=2,b=﹣1,
则11a2b+5abc﹣3ab2
=11×22×(﹣1)+5×2×(﹣1)×c﹣3×2×(﹣1)2
=﹣44﹣10c﹣6
=﹣50﹣10c,
所以不能求出该代数式的值.
52.解:(1)(4x2y﹣6xy2)﹣(3xy2﹣5x2y)
=4x2y﹣6xy2﹣3xy2+5x2y
=9x2y﹣9xy2;
(2)2(2x﹣7y)﹣3(3x﹣10y)
=4x﹣14y﹣9x+30y
=﹣5x+16y.
53.解:(1)5m﹣7n﹣8p+5n﹣9m﹣p
=(5﹣9)m+(﹣7+5)n+(﹣8﹣1)p
=﹣4m﹣2n﹣9p.
(2)x+2(3y2﹣2x)﹣4(2x﹣y2).
=x+6y2﹣4x﹣8x+4y2
=﹣11x+10y2.
54.解:(1)﹣2x﹣3+4x﹣x
=x﹣3;
(2)(2a2+a﹣1)﹣(2﹣3a+2a2)
=2a2+a﹣1﹣2+3a﹣2a2
=4a﹣3.
55.解:(1)根据题意得:2(y+3y+2.5x)=5x+8y;
(2)根据题意得:y 2.5x+3y 0.5x=4xy;
(3)当x=2,y=2.5时,S=4×2×2.5=20.
56.解:(1)原式=﹣2x2+x﹣4﹣x+2
=﹣2x2﹣2;
原式=2x2y+2xy2﹣2x2y+6x﹣2xy2﹣2y
=6x﹣2y.
十二.整式的加减—化简求值
57.解:原式=a2﹣3a2+2b2+3a2﹣3b2
=a2﹣b2;
当a=﹣3;b=﹣2时
原式=(﹣3)2﹣(﹣2)2
=9﹣4
=5.
58.解:(1)原式=﹣5a+3a﹣2+7﹣3a
=﹣5a+5.
(2)原式=3a2b﹣ab2+ab2﹣2a2b+1
=a2b+1,
当a=﹣2,b=3时,
原式=4×3+1
=13.
59.解:(1)原式=a+6a2+3a﹣6a2
=4a,
当a=1时,
原式=4.
(2)原式=(a2+2ab+b2﹣a2+2ab﹣b2)
=×4ab
=ab.
60.解:原式=4x﹣4﹣2x2﹣2+2x2﹣x
=3x﹣6,
当x=﹣2时,
原式=3×(﹣2)﹣6
=﹣6﹣6
=﹣12.
一.代数式
1.下列各式中,符合代数式书写规则的是( )
A. B. C. D.2y÷z
2.下列各式符合代数式书写规范的是( )
A. B.a×3 C.2m﹣1个 D.
3.下列各式:ab 2,m÷2n,xy,1a,其中符合代数式书写规范的有 个.
二.列代数式
4.某商品标价x元,进价为400元,在商场开展的促销活动中,该商品按8折销售获利( )
A.(8x﹣400)元 B.(400×8﹣x)元
C.(0.8x﹣400)元 D.(400×0.8﹣x)元
5.用式子表示“a的2倍与b的差的平方”,正确的是( )
A.2(a﹣b)2 B.2a﹣b2 C.(a﹣2b)2 D.(2a﹣b)2
6.如图是一块长为a,宽为b(a>b)的长方形空地,要将阴影部分绿化,则阴影面积是( )
A.a2b2 B.ab﹣πa2 C. D.
7.如图,长方形纸片上画有两个完全相同的阴影长方形,那么剩余的非阴影长方形的周长为 (用含a,b的代数式表示).
8.如图,甲、乙都是长方形,边长的数据如图所示(其中m为正整数).
(1)用含m的代数式表示:图中的甲长方形的面积S1= ,乙长方形的面积S2= ;
(2)请你先判断S1与S2的大小关系,并说明理由;
(3)现有一正方形,其周长与图中的甲长方形周长相等,试探究:该正方形面积S与图中的甲长方形面积S1的差(即S﹣S1)是一个常数,求出这个常数.
三.代数式求值
9.按如图所示的运算程序,能使运算输出结果为﹣5的是( )
A.x=1,y=﹣2 B.x=1,y=2 C.x=﹣1,y=2 D.x=﹣1,y=﹣2
10.已知代数式x+2y+1的值是3,则代数式2x+4y+1的值是( )
A.4 B.5 C.7 D.不能确定
11.已知2y2+y﹣2的值为3,则4y2+2y+1的值为( )
A.10 B.11 C.10或11 D.3或11
12.已知|a+5|+|b﹣3|=0,则a+b= .
13.按照如图所示的程序计算,若x=3,则输出的结果是 .
14.已知x﹣2y=1,则代数式3x﹣6y+2020的值是 .
15.如图,学校操场主席台前计划修建一块凹字形花坛.(单位:米)
(1)用含a,b的整式表示花坛的面积;
(2)若a=4,b=3,工程费为500元/平方米,求建花坛的总工程费为多少元?
16.为了提高业主的宜居环境,在某居民区的建设中,因地制宜规划修建一个广场(图中阴影部分).
(1)用含m、n的代数式表示该广场的周长;
(2)用含m、n的代数式表示该广场的面积;
(3)当m=6,n=8时,求出该广场的周长和面积.
四.同类项
17.已知﹣5xay与2x2yb为同类项,则a﹣b的值为( )
A.1 B.2 C.3 D.4
18.下列各式中,是5x2y的同类项的是( )
A.x2y B.﹣3x2yz C.3a2b D.5x3
19.若a2n+1b2与﹣5b2a3n﹣2是同类项,则n= .
五.合并同类项
20.下列运算正确的是( )
A.3a+2a=5a2 B.3a+3b=3ab
C.a5﹣a2=a3 D.2a2b﹣a2b=a2b
21.下列计算正确的是( )
A.﹣a2﹣a2=﹣2a2 B.3a2+a=4a2
C.4a﹣2a=2 D.2a2﹣a=a
22.下列各式中,正确的是( )
A.x2y﹣2x2y=﹣x2y B.2a+3b=5ab
C.7ab﹣3ab=4 D.a3+a2=a5
23.若2xm﹣3y5与﹣3x2yn+2的和是单项式,则m+n= .
24.合并同类项:5m+2n﹣m﹣3n.
六.去括号与添括号
25.下列变形正确的是( )
A.﹣(a+2)=a﹣2 B.﹣(2a﹣1)=﹣2a+1
C.﹣a+1=﹣(a﹣1) D.1﹣a=﹣(a+1)
26.下列去括号正确的是( )
A.﹣3(b﹣1)=﹣3b+1 B.﹣3(a﹣2)=﹣3a﹣6
C.﹣3(b﹣1)=3﹣3b D.﹣3(a﹣2)=3a﹣6
27.下列去括号中,正确的是( )
A.a2﹣(2a﹣1)=a2﹣2a﹣1
B.a2+(﹣2a﹣3)=a2﹣2a+3
C.3a﹣[5b﹣(2c﹣1)]=3a﹣5b+2c﹣1
D.﹣(a+b)+(c﹣d)=﹣a﹣b﹣c+d
28.下列各式,去括号正确的是( )
A.a+(b﹣c)+d=a﹣b+c﹣d B.a﹣(b﹣c+d)=a﹣b﹣c+d
C.a﹣(b﹣c+d)=a﹣b+c﹣d D.a﹣(b﹣c+d)=a﹣b+c+d
七.规律型:数字的变化类
29.将一列有理数﹣1,2,﹣3,4,﹣5,6,…,按如图所示进行排列,则﹣2021应排在( )
A.A位置 B.B位置 C.D位置 D.E位置
30.小刚在做数学题时,发现下面有趣的结果:
第1行:3﹣2=1
第2行:8+7﹣6﹣5=4
第3行:15+14+13﹣12﹣11﹣10=9
第4行:24+23+22+21﹣20﹣19﹣18﹣17=16
……
根据以上规律,“2021”在第m行,从左往右数第n个,那么m+n= .
31.如图是一根起点为1的数轴,现有同学将它弯折,弯折后虚线上由左至右第1个数是1,第2个数是13,第3个数是41,…,依此规律,第7个数是 .
32.观察下列式子,
①=1﹣,
②=﹣,
③=﹣,
…
(1)用正整数n表示这个规律 ;
(2)设F(n)=++…+,解决下列问题:
①F(10)= ;
②问:F(1)+++…+与F(n)相等吗?并说明理由.
八.整式
33.下列说法中,不正确的是( )
A.﹣ab2c的系数是﹣1,次数是4
B.﹣1是整式
C.6x2﹣3x+1的项是6x2、﹣3x,1
D.2πR+πR2是三次二项式
34.下列说法中正确的是( )
A.不是整式 B.﹣3x3y的次数是4
C.4ab与4xy是同类项 D.是单项式
九.单项式
35.在代数式:a,m+6,﹣5,a2b﹣2ab,3mn,中,单项式有( )
A.2个 B.3个 C.4个 D.5个
36.单项式﹣的系数是 ,次数是 .
37.单项式﹣的系数是 ,次数是 .
十.多项式
38.下列说法中,正确的是( )
A.单项式xy2的系数是x
B.单项式﹣5x2的次数为﹣5
C.多项式x2+2x+18是二次三项式
D.多项式x2+y2﹣1的常数项是1
39.要使多项式6x+5y﹣3+2ky+4k不含y的项,则k的值是( )
A.0 B. C. D.﹣
40.多项式3是( )
A.三次四项式 B.三次三项式 C.四次四项式 D.二次四项式
41.多项式ab2﹣5ab+2b﹣1的次数是 ,常数项是 .
42.当m= 时,多项式x2﹣mxy﹣3y2中不含xy项.
43.若关于x的多项式2x3+2mx2﹣5x﹣8x2﹣1不含二次项,则m= .
44.多项式﹣a3b﹣7ab﹣6ab4+1是 次 项式,它最高项的系数是 .
45.如果x+y=3,xy=2,则多项式x2y+xy2的值为 .
46.下列代数式中的哪些是单项式,哪些是多项式,哪些是整式?
,4xy,,,x2+x+,0,,m,﹣2.01×105
整式集合:{ …}
单项式集合:{ …}
多项式集合:{ …}.
47.已知代数式3xn﹣(m﹣1)x+1是关于x的三次二项式,求m、n的条件.
十一.整式的加减
48.若关于a,b的多项式3(a2﹣2ab﹣b2)﹣(a2+mab+2b2)中不含有ab项,则m= .
49.多项式8x2﹣3x+5与3x3+2mx2﹣5x+7相加后不含x的二次项,则常数m的值等于 .
50.化简
(1)3m+2n﹣5m﹣n;
(2)(5a﹣3b)﹣3(a﹣2b).
51.在整式的加减运算练习课上,小明同学将“2A﹣B”看成“A﹣2B”,算得错误结果是4a2b﹣3ab2+4abc,已知A=6a2b﹣ab2+2abc.请你解决以下问题:
(1)求出整式B;
(2)求出2A﹣B;
(3)若增加条件:a,b满足|a﹣2|+(b+1)2=0,你能求出(2)中代数式的值吗?如果能,请求出最后的值;如果不能,请说明理由.
52.化简:
(1)(4x2y﹣6xy2)﹣(3xy2﹣5x2y);
(2)2(2x﹣7y)﹣3(3x﹣10y).
53.化简:
(1)5m﹣7n﹣8p+5n﹣9m﹣p; (2)x+2(3y2﹣2x)﹣4(2x﹣y2).
54.化简:
(1)﹣2x﹣3+4x﹣x; (2)(2a2+a﹣1)﹣(2﹣3a+2a2).
55.如图,一个大长方形中剪下两个大小相同的小长方形(有关线段的长如图所示)留下一个“T”型的图形(阴影部分).
(1)用含x,y的代数式表示阴影部分的周长;
(2)用含x,y的代数式表示阴影部分的面积;
(3)当x=2,y=2.5时,计算阴影部分的面积.
56.化简:
(1)(﹣4x2+2x﹣8)﹣2(x﹣1)
(2)2(x2y+xy2)﹣2(x2y﹣3x)﹣2xy2﹣2y
十二.整式的加减—化简求值
57.先化简,后求值:a2﹣(3a2﹣2b2)+3(a2﹣b2),其中a=﹣3,b=﹣2.
58.解下列各题:
(1)化简:﹣5a+(3a﹣2)+(7﹣3a);
(2)先化简,再求值:3a2b﹣ab2﹣(﹣ab2+2a2b﹣1)其中a=﹣2,b=3.
59.化简、求值:
(1)先化简、再求值:(a+6a2)+3(a﹣2a2),其中a=1;
(2)化简:已知A=a2﹣2ab+b2,B=a2+2ab+b2,求(B﹣A).
60.先化简,再求值:4(x﹣1)﹣2(x2+1)+(4x2﹣2x),其中x=﹣2.
参考答案
一.代数式
1.解:A、符合代数式书写规则.
B、不符合代数式书写规则,应该为.
C、不符合代数式书写规则,应该为﹣.
D、不符合代数式书写规则,应改为.
故选:A.
2.解:A、除法按照分数的写法来写,原书写规范,故A符合题意;
B、数字与字母相乘时,数字要写在字母的前面且省略乘号,原书写不规范,故B不符合题意;
C、代数和后面写单位要加括号,原书写不规范,故C不符合题意;
D、带分数要写成假分数的形式,原书写不规范,故D不符合题意;
故选:A.
3.解:在ab 2,m÷2n,xy,1a,中,符合代数式书写规范的有xy,,共2个;
故答案为:2.
二.列代数式
4.解:由题意可得,
该商品按8折销售获利为:(0.8x﹣400)元,
故选:C.
5.解:a的2倍为2a,与b的差的平方为(2a﹣b)2
故选:D.
6.解:由图可得,
阴影部分的面积是:ab﹣=,
故选:C.
7.解:由题意可得,非阴影长方形的周长为:2(b﹣a)+2b=4b﹣2a.
故答案为:4b﹣2a.
8.解:(1)S1=(m+1)(m+7)=m2+8m+7,
S2=(m+2)(m+4)=m2+6m+8.
故答案为:m2+8m+7,m2+6m+8;
(2)S1>S2,理由如下:
S1﹣S2=(m2+8m+7)﹣(m2+6m+8)=2m﹣1,
∵m为正整数,
∴2m﹣1>0,
∴S1>S2;
(3)图中甲的长方形周长为2(m+7+m+1)=4m+16,
∴该正方形边长为m+4,
∴S﹣S1=(m+4)2﹣(m2+8m+7)=9,
∴这个常数为9.
三.代数式求值
9.解:A、当x=1,y=﹣2时,输出结果为1+4=5,不符合题意;
B、当x=1,y=2时,输出结果为1﹣4=﹣3,不符合题意;
C、当x=﹣1,y=2时,输出结果为﹣1﹣4=﹣5,符合题意;
D、当x=﹣1,y=﹣2时,输出结果为﹣1+4=3,不符合题意,
故选:C.
10.解:根据题意得
x+2y+1=3,
∴x+2y=2,
那么2x+4y+1=2(x+2y)+1=2×2+1=5.
故选:B.
11.解:∵2y2+y﹣2的值为3,
∴2y2+y﹣2=3,
∴2y2+y=5,
∴2(2y2+y)=4y2+2y=10,
∴4y2+2y+1=11.
故选:B.
12.解:由题意得a+5=0,b﹣3=0,
解得a=﹣5,b=3,
所以a+b=﹣5+3=﹣2.
故答案为:﹣2.
13.解:当x=3时,x2﹣10=9﹣10=﹣1<0,
于是再把x=﹣1输入,x2﹣10=1﹣10=﹣9<0,
再把x=﹣9输入,x2﹣10=81﹣10=71>0,
因此输出的数为:71,
故答案为:71.
14.解:∵x﹣2y=1,
∴3x﹣6y+2020
=3(x﹣2y)+2020
=3×1+2020
=3+2020
=2023.
故答案为:2023.
15.解:(1)(a+3b+a)(2a+b)﹣2a 3b
=4a2+8ab+3b2﹣6ab
=(4a2+2ab+3b2)(平方米).
答:花坛的面积是(4a2+2ab+3b2)平方米.
(2)当a=4,b=3时,
4a2+2ab+3b2
=4×42+4×2×3+3×32
=115(平方米),
115×500=57500(元).
答:建花坛的总工程费为57500元.
16.解:(1)C=6m+4n;
(2)S=2m×2n﹣m(2n﹣n﹣0.5n)
=4mn﹣0.5mn
=3.5mn;
(3)把m=6,n=8,代入周长6m+4n=6×6+4×8=68,
把m=6,n=8,代入面积3.5mn=3.5×6×8=168.
四.同类项
17.解:∵﹣5xay与2x2yb是同类项,
∴a=2,b=1,
故a﹣b=2﹣1=1.
故选:A.
18.解:A.5x2y与x2y,所含的字母相同:x、y,它们的指数也相同,所以它们是同类项,故本选项符合题意;
B.5x2y与﹣3x2yz,所含的字母不相同,所以它们不是同类项,故本选项不合题意;
C.5x2y与3a2b,所含的字母不相同,所以它们不是同类项,故本选项不合题意;
D.5x2y与5x3,所含的字母不相同,所以它们不是同类项,故本选项不合题意.
故选:A.
19.解:∵a2n+1b2与﹣5b2a3n﹣2是同类项,
∴2n+1=3n﹣2,
解得:n=3.
故答案为:3.
五.合并同类项
20.解:A、3a+2a=5a,故本选项不合题意;
B、3a与3b不是同类项,所以不能合并,故本选项不合题意;
C、a5与﹣a2不是同类项,所以不能合并,故本选项不合题意;
D、2a2b﹣a2b=a2b,故本选项符合题意.
故选:D.
21.解:A、﹣a2﹣a2=﹣2a2=(﹣1﹣1)a2=﹣2a2,故A正确;
B、不是同类项不能合并,故B错误;
C、4a﹣2a=(4﹣2)a=2a,故C错误;
D、不是同类项不能合并,故D错误.
故选:A.
22.解:A、x2y﹣2x2y=﹣x2y,故A正确;
B、不是同类项,不能进一步计算,故B错误;
C、7ab﹣3ab=4ab,故C错误;
D、a3+a2=a5,不是同类项,故D错误.
故选:A.
23.解:∵2xm﹣3y5与﹣3x2yn+2的和是单项式,
∴2xm﹣3y5与﹣3x2yn+2是同类项,
∴m﹣3=2,n+2=5,
∴m=5,n=3,
∴m+n=5+3=8.
故答案为:8.
24.解:5m+2n﹣m﹣3n
=(5m﹣m)+(2n﹣3n)
=4m﹣n.
六.去括号与添括号
25.解:A、原式=﹣a﹣2,故本选项变形错误.
B、原式=﹣a+,故本选项变形错误.
C、原式=﹣(a﹣1),故本选项变形正确.
D、原式=﹣(a﹣1),故本选项变形错误.
故选:C.
26.解:A、﹣3(b﹣1)=﹣3b+3,故此选项错误;
B、﹣3(a﹣2)=﹣3a+6,故此选项错误;
C、﹣3(b﹣1)=3﹣3b,故此选项正确;
D、﹣3(a﹣2)=﹣3a+6,故此选项错误;
故选:C.
27.解:A,a2﹣(2a﹣1)=a2﹣2a+1,故此选项错误;
B,a2+(﹣2a﹣3)=a2﹣2a﹣3,故此选项错误;
C,3a﹣[5b﹣(2c﹣1)]=3a﹣5b+2c﹣1,故此选项正确;
D,﹣(a+b)+(c﹣d)=﹣a﹣b+c﹣d,故此选项错误;
故选:C.
28.解:A、a+(b﹣c)+d=a+b﹣c+d,故错误;
B、a﹣(b﹣c+d)=a﹣b+c﹣d,故错误;
D、a﹣(b﹣c+d)=a﹣b+c﹣d,故错误;
只有C符合运算方法,正确.
故选:C.
七.规律型:数字的变化类
29.解:由图可知,
每个凸起对应5个数字,这些数字的奇数都是负数,偶数都是正数,
∵(2021﹣1)÷5=2020÷5=404,
∴﹣2021应排在E位置,
故选:D.
30.解:∵(43+1)2﹣1=1935,
(44+1)2﹣1=2024,
∴2021这个数出现在第44行,左起第2024﹣2021+1=4个数.
∴m=44,n=4,
∴m+n=44+4=48,
故答案为48.
31.解:第二个数13=12+1=3×4+1,
第三个数41=40+1=5×8+1,
则第七个数=[5+(7﹣3)×2]×[8+(7﹣3)×4]+1=13×24+1=313.
故答案为:313.
32.解:(1)用正整数n表示这个规律为:,
等式右边=﹣===等式左边,
即等式成立,
故答案为:;
(2)①F(10)=++…+=1﹣++…+=1﹣=,
故答案为:;
②相等,理由如下:
F(1)+++…+=+++......+=+++......+=F(n),
即相等.
八.整式
33.解:A、﹣ab2c的系数是﹣1,次数是4,故A正确;
B、﹣1是整式,故B正确;
C、6x2﹣3x+1的项是6x2、﹣3x,1,故C正确;
D、2πR+πR2是二次二项式,故D错误;
故选:D.
34.解:A、是整式,故错误;
B、﹣3x3y的次数是4,正确;
C、4ab与4xy不是同类项,故错误;
D、不是单项式,是分式故错误.
故选:B.
九.单项式
35.解:代数式a,m+6,﹣5,a2b﹣2ab,3mn,中,单项式有:
a,﹣5,3mn,共有3个.
故选:B.
36.解:单项式﹣的系数是:﹣,
次数是:3.
故答案为:﹣,3.
37.解:单项式﹣的系数是﹣,次数是5;
故答案为:﹣;5.
十.多项式
38.解:A、单项式xy2的系数是,原说法错误,故此选项不符合题意;
B、单项式﹣5x2的次数为2,原说法错误,故此选项不符合题意;
C、多项式x2+2x+18是二次三项式,原说法正确,故此选项符合题意;
D、多项式x2+y2﹣1的常数项是﹣1,原说法错误,故此选项不符合题意,
故选:C.
39.解:要使多项式6x+5y﹣3+2ky+4k不含y的项,则y的系数应为0,
多项式6x+5y﹣3+2ky+4k中,5y和2ky两项含有y,要求这两项的系数互为相反数,
合并同类项时,
为2k+5=0,
即k=﹣.
故选:D.
40.解:因为多项式3的各项的次数分别为2,3,1,0,
由于多项式的次数是“多项式中次数最高的项的次数”,
所以多项式3的次数是3,
又因为它有四个单项式组成,所以它是三次四项式.
故选:A.
41.解:多项式ab2﹣5ab+2b﹣1的次数是3,常数项为﹣1,
故答案为:3,﹣1.
42.解:∵多项式x2﹣mxy﹣3y2中不含xy项,
∴﹣m+=0,
解得:m=.
故答案为:.
43.解:2x3+2mx2﹣5x﹣8x2﹣1=2x3+(2m﹣8)x2﹣5x﹣1,
∵关于x的多项式2x3+2mx2﹣5x﹣8x2﹣1不含二次项,
∴2m﹣8=0,
解得:m=4,
故答案为:4.
44.解:依题意得原式是一个五次四项式,它的最高项的系数是﹣6.
故填空答案:五,四,﹣6.
45.解:x2y+xy2=xy(x+y)=2×3=6.
46.解:整式集合:{,4xy,,0,m,﹣2.01×105 …};
单项式集合:{ 4xy,,0,m,﹣2.01×105 …};
多项式集合:{ …}.
故答案为:{,4xy,,0,m,﹣2.01×105 …};{ 4xy,,0,m,﹣2.01×105 …};{ …}.
47.解:∵代数式3xn﹣(m﹣1)x+1是关于x的三次二项式,
∴n=3,m﹣1=0,
解得:m=1,n=3.
十一.整式的加减
48.解:原式=3a2﹣6ab﹣3b2﹣a2﹣mab﹣2b2=2a2﹣(6+m)ab﹣5b2,
由于多项式中不含有ab项,
故﹣(6+m)=0,
∴m=﹣6,
故填空答案:﹣6.
49.解:∵多项式8x2﹣3x+5与3x3+2mx2﹣5x+7相加后不含x的二次项,
∴8x2+2mx2=(2m+8)x2,
∴2m+8=0,
解得m=﹣4.
故答案为﹣4.
50.解:(1)3m+2n﹣5m﹣n
=(3m﹣5m)+(2n﹣n)
=﹣2m+n;
(2)(5a﹣3b)﹣3(a﹣2b)
=5a﹣3b﹣3a+6b
=(5a﹣3a)+(﹣3b+6b)
=2a+3b.
51.解:(1)根据题意B=[(6a2b﹣ab2+2abc)﹣(4a2b﹣3ab2+4abc)]÷2
=(6a2b﹣ab2+2abc﹣4a2b+3ab2﹣4abc)÷2
=(2a2b﹣2abc+2ab2)÷2
=a2b﹣abc+ab2;
(2)2A﹣B
=2(6a2b﹣ab2+2abc)﹣(a2b﹣abc+ab2)
=12a2b﹣2ab2+4abc﹣a2b+abc﹣ab2
=11a2b+5abc﹣3ab2;
(3)∵|a﹣2|+(b+1)2=0,
∴a﹣2=0且b+1=0,
∴a=2,b=﹣1,
则11a2b+5abc﹣3ab2
=11×22×(﹣1)+5×2×(﹣1)×c﹣3×2×(﹣1)2
=﹣44﹣10c﹣6
=﹣50﹣10c,
所以不能求出该代数式的值.
52.解:(1)(4x2y﹣6xy2)﹣(3xy2﹣5x2y)
=4x2y﹣6xy2﹣3xy2+5x2y
=9x2y﹣9xy2;
(2)2(2x﹣7y)﹣3(3x﹣10y)
=4x﹣14y﹣9x+30y
=﹣5x+16y.
53.解:(1)5m﹣7n﹣8p+5n﹣9m﹣p
=(5﹣9)m+(﹣7+5)n+(﹣8﹣1)p
=﹣4m﹣2n﹣9p.
(2)x+2(3y2﹣2x)﹣4(2x﹣y2).
=x+6y2﹣4x﹣8x+4y2
=﹣11x+10y2.
54.解:(1)﹣2x﹣3+4x﹣x
=x﹣3;
(2)(2a2+a﹣1)﹣(2﹣3a+2a2)
=2a2+a﹣1﹣2+3a﹣2a2
=4a﹣3.
55.解:(1)根据题意得:2(y+3y+2.5x)=5x+8y;
(2)根据题意得:y 2.5x+3y 0.5x=4xy;
(3)当x=2,y=2.5时,S=4×2×2.5=20.
56.解:(1)原式=﹣2x2+x﹣4﹣x+2
=﹣2x2﹣2;
原式=2x2y+2xy2﹣2x2y+6x﹣2xy2﹣2y
=6x﹣2y.
十二.整式的加减—化简求值
57.解:原式=a2﹣3a2+2b2+3a2﹣3b2
=a2﹣b2;
当a=﹣3;b=﹣2时
原式=(﹣3)2﹣(﹣2)2
=9﹣4
=5.
58.解:(1)原式=﹣5a+3a﹣2+7﹣3a
=﹣5a+5.
(2)原式=3a2b﹣ab2+ab2﹣2a2b+1
=a2b+1,
当a=﹣2,b=3时,
原式=4×3+1
=13.
59.解:(1)原式=a+6a2+3a﹣6a2
=4a,
当a=1时,
原式=4.
(2)原式=(a2+2ab+b2﹣a2+2ab﹣b2)
=×4ab
=ab.
60.解:原式=4x﹣4﹣2x2﹣2+2x2﹣x
=3x﹣6,
当x=﹣2时,
原式=3×(﹣2)﹣6
=﹣6﹣6
=﹣12.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
