1.1.2弧度制 课件
图片预览






文档简介
(共25张PPT)
1、在0°~360°范围内,找出与-600°角终边相同的角,并判定它是第几象限角.
-600°=120°-360°X 2
第二象限角.
2、写出与-600°角终边相同的角的集合S,并把集合S中适合不等式-720°≤ β<720°的元素β写出来.
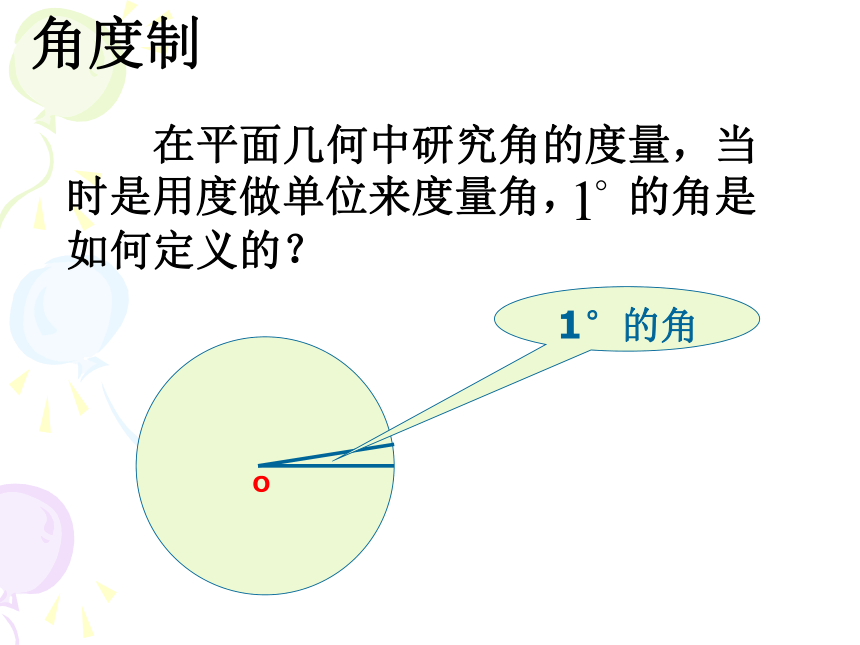
在平面几何中研究角的度量,当时是用度做单位来度量角, 的角是如何定义的?
O
1°的角
角度制
我们把用度做单位来度量角的制度叫做角度制,在数学和其他许多科学研究中还要经常用到一种度量角的制度
—弧度制,它是如何定义呢?
在角度制下,当把两个带着度、分、秒各单位的角相加、相减时,由于运算进率非十进制,总给我们带来不少困难.那么我们能否重新选择角单位,使在该单位制下两角的加、减运算与常规的十进制加减法一样去做呢?
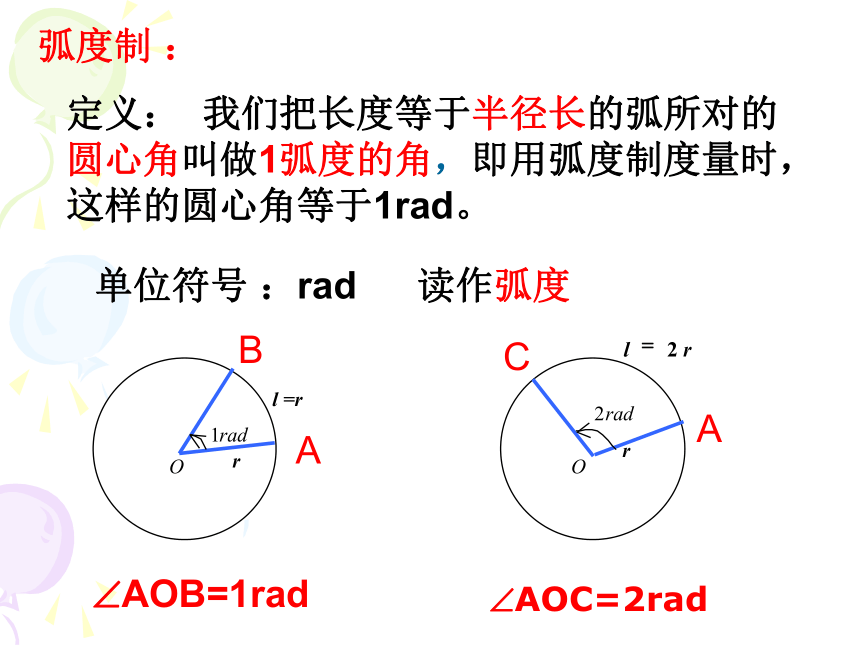
弧度制 :
单位符号 :rad
读作弧度
定义: 我们把长度等于半径长的弧所对的
圆心角叫做1弧度的角,即用弧度制度量时,
这样的圆心角等于1rad。
AOB=1rad
o
A
B
rad
1
O
l =r
r
o
A
C
rad
2
O
r
r
l
2
=
AOC=2rad
(1)正角的弧度数是正数,负角的弧度数是负数,
零角的弧度数是0
(2)角 的弧度数的绝对值
(
(4)用角度制和弧度制来度量零角,单位不同,
但量数相同(都是0)
(5)用角度制和弧度制来度量任一非零角,
单位不同,量数也不同。
(3)以弧度作为单位来度量角的单位制,叫做弧度制
把角度换成弧度
把弧度换成角度
角度与弧度间的换算
注意几点:
1.度数与弧度数的换算也可借助“计算器”
《中学数学用表》进行
2.今后在具体运算时,“弧度”二字和单位
符号“rad”可以省略 如:3表示3rad
sin 表示 rad角的正弦
3.一些特殊角的度数与弧度数的对应值应
该记住(见课本P8表)
4.应确立如下的概念:角的概念推广之后,
无论用角度制还是弧度制都能在角的集合
与实数的集合之间建立一种一一对应的关系。
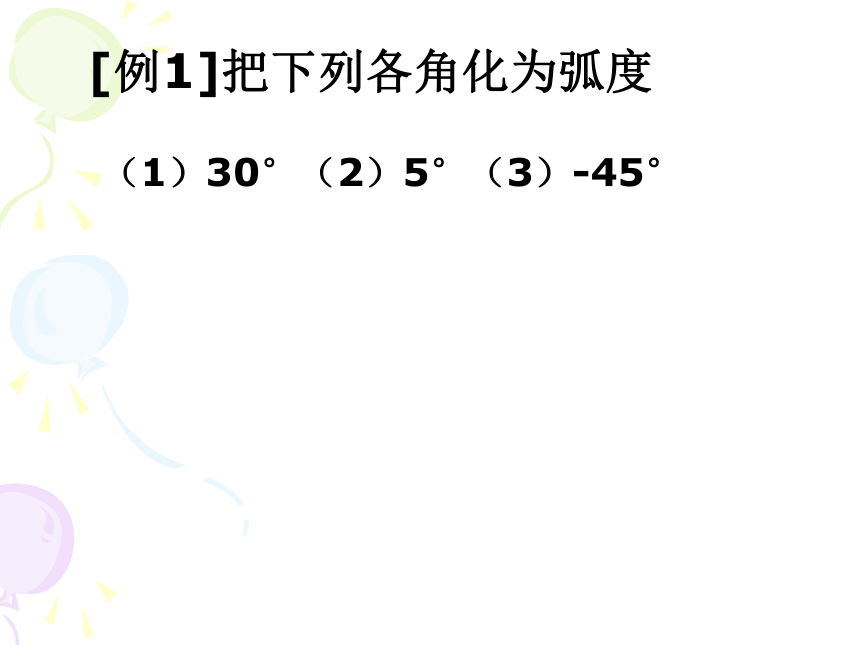
[例1]把下列各角化为弧度
(1)30°(2)5°(3)-45°
角度制与弧度制互化时要抓住
弧度 这个关键.
[例2]把下列 各角化为度:
弧度
360
270
180
90
60
45
30
度
练习:填表
15
45
75
135
300
0
弧度
60
30
0
度
270
90
度
弧度
角度制与弧度制的比较
①弧度制是以“弧度”为单位度量角的制度,角度制是以“度”为单位度量角的制度;
的大小,而 是圆的 所对的圆心角(或该弧)
②1弧度是等于半径长的圆弧所对的圆心角(或该弧)
的大小;
③不论是以“弧度”还是以“度”为单位的角的大小都是一
个与半径大小无关的定值.
终边相同的角
(1)用角度表示
(2)用弧度表示
与 终边相同的角可以表示为:
它们构成一个集合:
与 终边相同的角可以表示为:
它们构成一个集合:
把下列各角化成
的形式:
[例3]
(1) ;(2) ;(3) .
已知扇形OAB的中心角为4,其面积2cm2,求扇形的周长和弦AB的长。
弧长公式
1、角度制下的弧长公式
角度制下的扇形面积公式
2、弧度制下的弧长公式
弧度制制下的扇形面积公式
[例4].求图中公路弯道处弧 的长
(精确到 ,图中长度单位: ).
例5 已知扇形的周长为10cm, 面积为4cm2,求扇形的圆心角.
解: 设扇形的圆心角的弧度数为 , 弧长为l,半径为R,
分析:要求圆心角,根据公式 ,需求弧长l及半径R.
根据题意:
①
②
由①得 ,
代入②得
当R=1时,l=8cm时,
当R=4时,l=2cm时,
舍去
∴所求扇形的圆心角的弧度数为
1、已知扇形周长为6cm,面积为2cm2,则扇形圆心角的弧度数为
A、1 B、4 C、1或4 D、2或4
C
2、当圆心角α=-216o,弧长l =7πcm时,其半径r=________
3、在半径为 的圆中,圆心角为周角的 的角所对圆弧的长为___________
40
4、若2 rad的圆心角所对的弧长是4cm,则这个圆心角所在扇形的面积为_________
4cm2
8.已知扇形的周长为20 cm,当扇形的中心角为多大时,它有最大面积,最大面积是多少
练习7:当扇形的中心角为600,半径为10cm,求扇形的弧长及该弧所在的弓形面积
L=10π/3
600=π/3
作业
课本第10页
第7、8、 9、10题
例5 用弧度制表示
1、在0°~360°范围内,找出与-600°角终边相同的角,并判定它是第几象限角.
-600°=120°-360°X 2
第二象限角.
2、写出与-600°角终边相同的角的集合S,并把集合S中适合不等式-720°≤ β<720°的元素β写出来.
在平面几何中研究角的度量,当时是用度做单位来度量角, 的角是如何定义的?
O
1°的角
角度制
我们把用度做单位来度量角的制度叫做角度制,在数学和其他许多科学研究中还要经常用到一种度量角的制度
—弧度制,它是如何定义呢?
在角度制下,当把两个带着度、分、秒各单位的角相加、相减时,由于运算进率非十进制,总给我们带来不少困难.那么我们能否重新选择角单位,使在该单位制下两角的加、减运算与常规的十进制加减法一样去做呢?
弧度制 :
单位符号 :rad
读作弧度
定义: 我们把长度等于半径长的弧所对的
圆心角叫做1弧度的角,即用弧度制度量时,
这样的圆心角等于1rad。
AOB=1rad
o
A
B
rad
1
O
l =r
r
o
A
C
rad
2
O
r
r
l
2
=
AOC=2rad
(1)正角的弧度数是正数,负角的弧度数是负数,
零角的弧度数是0
(2)角 的弧度数的绝对值
(
(4)用角度制和弧度制来度量零角,单位不同,
但量数相同(都是0)
(5)用角度制和弧度制来度量任一非零角,
单位不同,量数也不同。
(3)以弧度作为单位来度量角的单位制,叫做弧度制
把角度换成弧度
把弧度换成角度
角度与弧度间的换算
注意几点:
1.度数与弧度数的换算也可借助“计算器”
《中学数学用表》进行
2.今后在具体运算时,“弧度”二字和单位
符号“rad”可以省略 如:3表示3rad
sin 表示 rad角的正弦
3.一些特殊角的度数与弧度数的对应值应
该记住(见课本P8表)
4.应确立如下的概念:角的概念推广之后,
无论用角度制还是弧度制都能在角的集合
与实数的集合之间建立一种一一对应的关系。
[例1]把下列各角化为弧度
(1)30°(2)5°(3)-45°
角度制与弧度制互化时要抓住
弧度 这个关键.
[例2]把下列 各角化为度:
弧度
360
270
180
90
60
45
30
度
练习:填表
15
45
75
135
300
0
弧度
60
30
0
度
270
90
度
弧度
角度制与弧度制的比较
①弧度制是以“弧度”为单位度量角的制度,角度制是以“度”为单位度量角的制度;
的大小,而 是圆的 所对的圆心角(或该弧)
②1弧度是等于半径长的圆弧所对的圆心角(或该弧)
的大小;
③不论是以“弧度”还是以“度”为单位的角的大小都是一
个与半径大小无关的定值.
终边相同的角
(1)用角度表示
(2)用弧度表示
与 终边相同的角可以表示为:
它们构成一个集合:
与 终边相同的角可以表示为:
它们构成一个集合:
把下列各角化成
的形式:
[例3]
(1) ;(2) ;(3) .
已知扇形OAB的中心角为4,其面积2cm2,求扇形的周长和弦AB的长。
弧长公式
1、角度制下的弧长公式
角度制下的扇形面积公式
2、弧度制下的弧长公式
弧度制制下的扇形面积公式
[例4].求图中公路弯道处弧 的长
(精确到 ,图中长度单位: ).
例5 已知扇形的周长为10cm, 面积为4cm2,求扇形的圆心角.
解: 设扇形的圆心角的弧度数为 , 弧长为l,半径为R,
分析:要求圆心角,根据公式 ,需求弧长l及半径R.
根据题意:
①
②
由①得 ,
代入②得
当R=1时,l=8cm时,
当R=4时,l=2cm时,
舍去
∴所求扇形的圆心角的弧度数为
1、已知扇形周长为6cm,面积为2cm2,则扇形圆心角的弧度数为
A、1 B、4 C、1或4 D、2或4
C
2、当圆心角α=-216o,弧长l =7πcm时,其半径r=________
3、在半径为 的圆中,圆心角为周角的 的角所对圆弧的长为___________
40
4、若2 rad的圆心角所对的弧长是4cm,则这个圆心角所在扇形的面积为_________
4cm2
8.已知扇形的周长为20 cm,当扇形的中心角为多大时,它有最大面积,最大面积是多少
练习7:当扇形的中心角为600,半径为10cm,求扇形的弧长及该弧所在的弓形面积
L=10π/3
600=π/3
作业
课本第10页
第7、8、 9、10题
例5 用弧度制表示
