1.3三角函数的诱导公式 课件
文档属性
| 名称 | 1.3三角函数的诱导公式 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 328.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-08-15 00:00:00 | ||
图片预览







文档简介
(共29张PPT)
一切立体图形中最美的是球形,一切平面图形中最美的是圆形。
——— 毕达哥拉斯学派
圆是第一个最简单、最完美的图形。
—— 布龙克尔
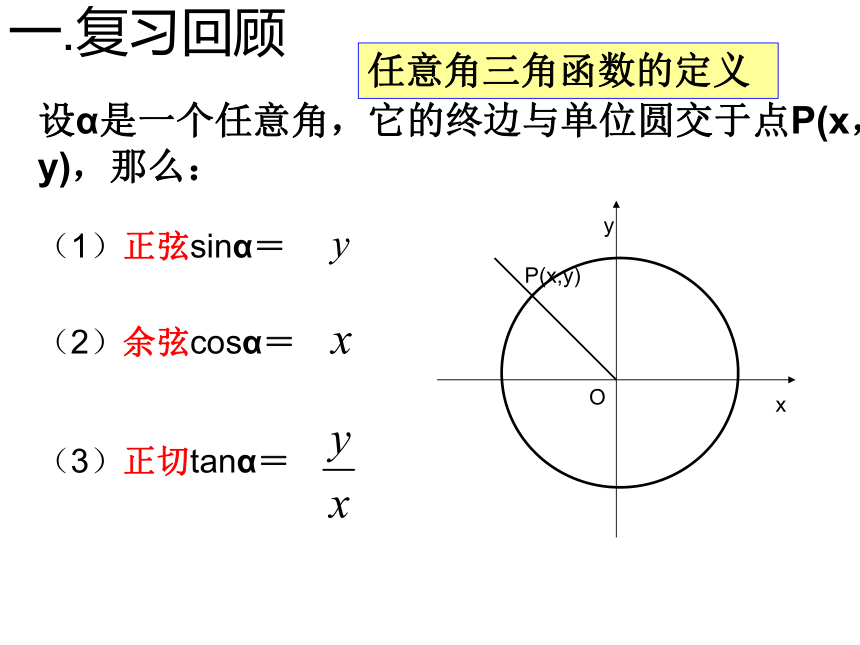
任意角三角函数的定义
设α是一个任意角,它的终边与单位圆交于点P(x,y),那么:
(1)正弦sinα=
(2)余弦cosα=
(3)正切tanα=
一.复习回顾
x
y
O
P(x,y)
问题探究
1.终边相同的角的同一三角函数值有什么关系
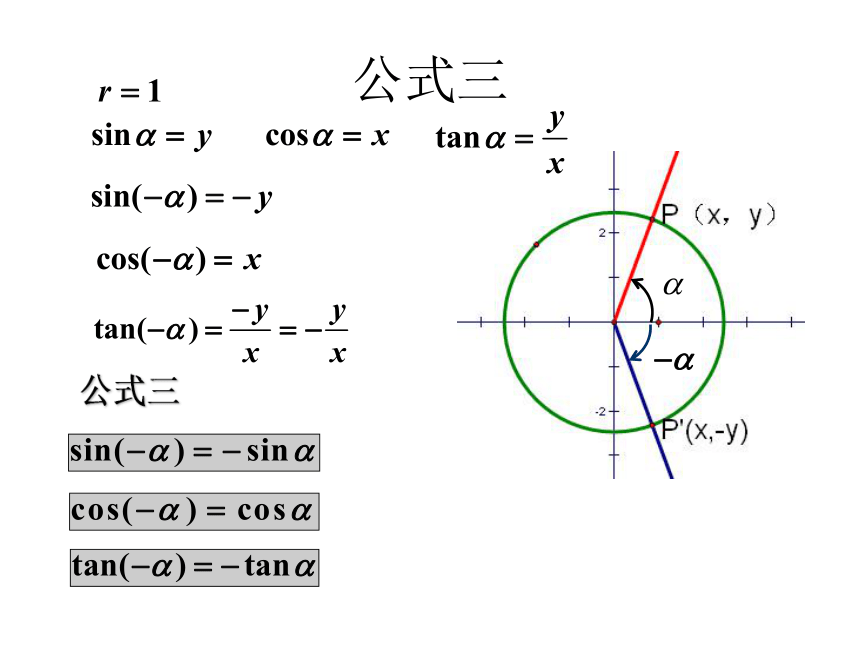
2.角 -α与α的终边 有何位置关系
3.角 -α与α的终边 有何位置关系
4.角 +α与α的终边 有何位置关系
相等
终边关于x轴对称
终边关于y轴对称
终边关于原点对称
终边相同的角的同一三角函数值相等
(公式一)
请同学们思考回答点 关于原点、 轴、 轴对称的三个点的坐标是什么
已知任意角 的终边与单位圆相交于点 ,
点 关于原点对称点 ,关于
轴对称点 ,关于 轴对称点
二、思考:
公式二
探究1
形如 的三角函数值与 的三角函数值之间的关系
我们再来研究角 与 的三角函数值之间的关系
探究2
公式三
公式三
探究3
公式四
公式四
公式一:
公式二:
公式三:
公式四:
简记为“函数名不变,符号看象限”
的三角函数值,等于 的同名三角函数值前面加上把 看作锐角时原函数值的符号。
三.发现规律:
公式一、二、三、四,都叫做诱导公式.
1、通过例题,你能说说诱导公式的作用以及化任意角的三角函数为锐角三角函数的一般思路吗?
小结
任意负角的
三角函数
任意正角的
三角函数
三角函数
的
锐角的三角函数
用公式
三或一
用公式一
用公式
二或四
上述过程体现了由未知到已知的化归思想。
例1.求下列三角函数值
四.例题分析
填写下表
练习反馈
例2 化简:
练习反馈
请同学们思考回答点 关于直线 对称的点的坐标是什么
已知任意角 的终边与单位圆相交于点 ,
探索研究
y
x
0
1
-1
-1
1
P(x,y)
P′(y,x)
总结:
1.公式五,六口诀:
函数名改变,符号看象限;
.
11
注意:
看成锐角,原函数值的符号
诱导公式记忆口诀:
奇变偶不变
符号看象限
例题与练习
例题与练习
求下列三角函数值
(1)sin(-12000)
(2)cos(47 /6)
求三角式sin(-12000)·cos(12900)+cos(-10200)·
sin(-10500)+tan9450
2
计算 cos( /5)+ cos(2 /5)+
cos(3 /5)+ cos(4 /5)
0
例题与练习
2 已知cos (750+ )=1/3,
求cos(1050- )+cos(2850- )
练习1 已知sin( /4+ )=1/2,则sin(3 /4- )的
值是 。
1/2
0
例题与练习
已知角 的终边上的一点P(3a,4a) (a<0)
则cos(5400- )的值是 。
3/5
2 cos( -8 /3)+cos( +13 /3)= .
0
例题与练习
例4 化简
练习1 求sin(2n +2 /3)·cos(n +4 /3)的值(n Z)
2 化简 cos[(4n+1) /4+x]+ cos[(4n-1) /4-x]
当n为奇数时,原式=-2cos( /4+x)
当n为偶数时,原式=2cos( /4+x)
当n为偶数时,
当n为奇数时,
2、你能概括以下研究诱导公式的思想方法吗?
圆的对称性
角的终边的对称性
对称点的数量关系
角之间的数量关系
诱导公式
小结
“对称是美的基本形式”
作 业
P28 第7题
P27 第2题
一切立体图形中最美的是球形,一切平面图形中最美的是圆形。
——— 毕达哥拉斯学派
圆是第一个最简单、最完美的图形。
—— 布龙克尔
任意角三角函数的定义
设α是一个任意角,它的终边与单位圆交于点P(x,y),那么:
(1)正弦sinα=
(2)余弦cosα=
(3)正切tanα=
一.复习回顾
x
y
O
P(x,y)
问题探究
1.终边相同的角的同一三角函数值有什么关系
2.角 -α与α的终边 有何位置关系
3.角 -α与α的终边 有何位置关系
4.角 +α与α的终边 有何位置关系
相等
终边关于x轴对称
终边关于y轴对称
终边关于原点对称
终边相同的角的同一三角函数值相等
(公式一)
请同学们思考回答点 关于原点、 轴、 轴对称的三个点的坐标是什么
已知任意角 的终边与单位圆相交于点 ,
点 关于原点对称点 ,关于
轴对称点 ,关于 轴对称点
二、思考:
公式二
探究1
形如 的三角函数值与 的三角函数值之间的关系
我们再来研究角 与 的三角函数值之间的关系
探究2
公式三
公式三
探究3
公式四
公式四
公式一:
公式二:
公式三:
公式四:
简记为“函数名不变,符号看象限”
的三角函数值,等于 的同名三角函数值前面加上把 看作锐角时原函数值的符号。
三.发现规律:
公式一、二、三、四,都叫做诱导公式.
1、通过例题,你能说说诱导公式的作用以及化任意角的三角函数为锐角三角函数的一般思路吗?
小结
任意负角的
三角函数
任意正角的
三角函数
三角函数
的
锐角的三角函数
用公式
三或一
用公式一
用公式
二或四
上述过程体现了由未知到已知的化归思想。
例1.求下列三角函数值
四.例题分析
填写下表
练习反馈
例2 化简:
练习反馈
请同学们思考回答点 关于直线 对称的点的坐标是什么
已知任意角 的终边与单位圆相交于点 ,
探索研究
y
x
0
1
-1
-1
1
P(x,y)
P′(y,x)
总结:
1.公式五,六口诀:
函数名改变,符号看象限;
.
11
注意:
看成锐角,原函数值的符号
诱导公式记忆口诀:
奇变偶不变
符号看象限
例题与练习
例题与练习
求下列三角函数值
(1)sin(-12000)
(2)cos(47 /6)
求三角式sin(-12000)·cos(12900)+cos(-10200)·
sin(-10500)+tan9450
2
计算 cos( /5)+ cos(2 /5)+
cos(3 /5)+ cos(4 /5)
0
例题与练习
2 已知cos (750+ )=1/3,
求cos(1050- )+cos(2850- )
练习1 已知sin( /4+ )=1/2,则sin(3 /4- )的
值是 。
1/2
0
例题与练习
已知角 的终边上的一点P(3a,4a) (a<0)
则cos(5400- )的值是 。
3/5
2 cos( -8 /3)+cos( +13 /3)= .
0
例题与练习
例4 化简
练习1 求sin(2n +2 /3)·cos(n +4 /3)的值(n Z)
2 化简 cos[(4n+1) /4+x]+ cos[(4n-1) /4-x]
当n为奇数时,原式=-2cos( /4+x)
当n为偶数时,原式=2cos( /4+x)
当n为偶数时,
当n为奇数时,
2、你能概括以下研究诱导公式的思想方法吗?
圆的对称性
角的终边的对称性
对称点的数量关系
角之间的数量关系
诱导公式
小结
“对称是美的基本形式”
作 业
P28 第7题
P27 第2题
