1.4.2b正弦函数、余弦函数的性质--单调性 课件
文档属性
| 名称 | 1.4.2b正弦函数、余弦函数的性质--单调性 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 134.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-08-15 00:00:00 | ||
图片预览



文档简介
(共12张PPT)
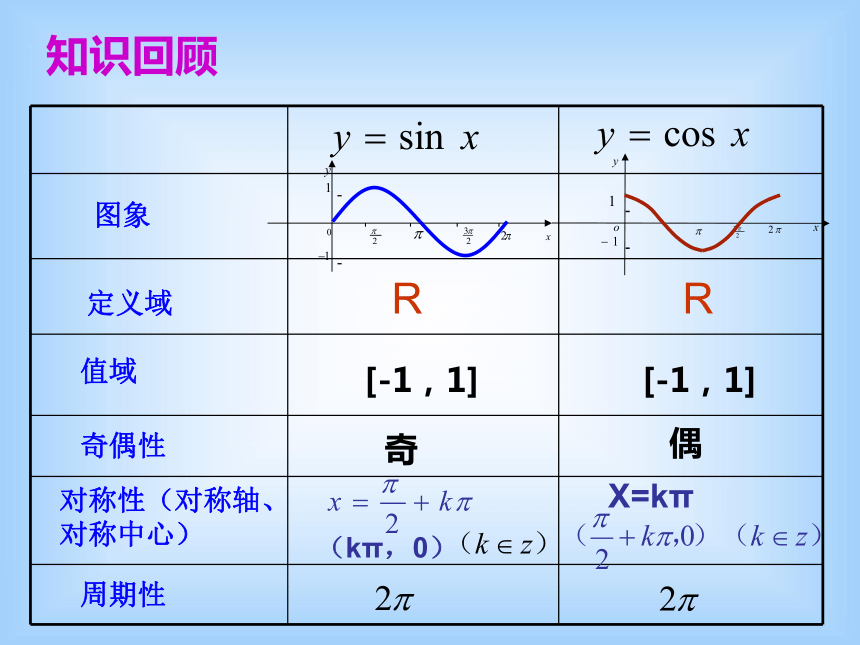
定义域
图象
值域
奇偶性
对称性(对称轴、 对称中心)
周期性
R
R
[-1,1]
[-1,1]
奇
偶
X=kπ
-
-
-
-
-
-
-
-
(kπ,0)
知识回顾
-1 1
1 -1
-1 1
1 -1
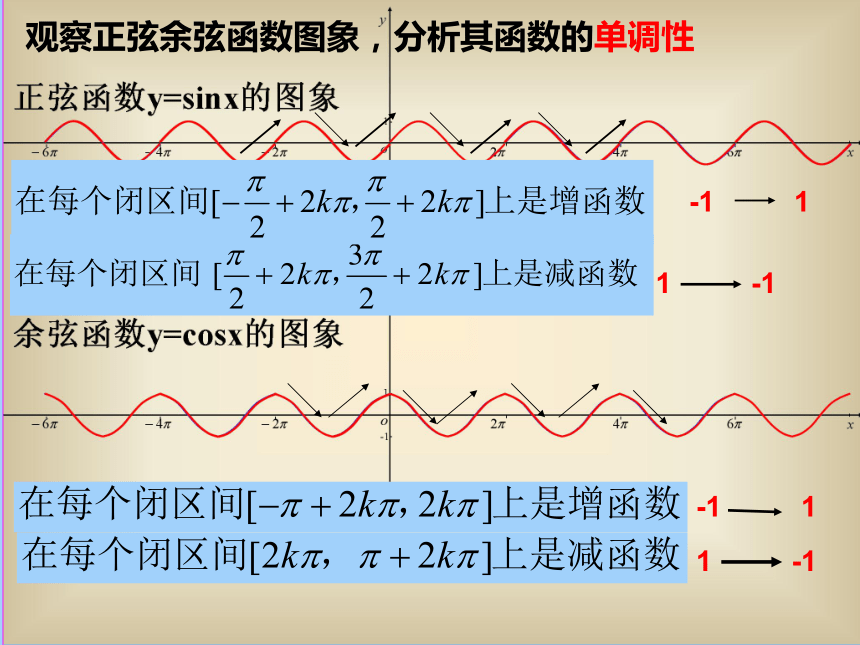
观察正弦余弦函数图象,分析其函数的单调性
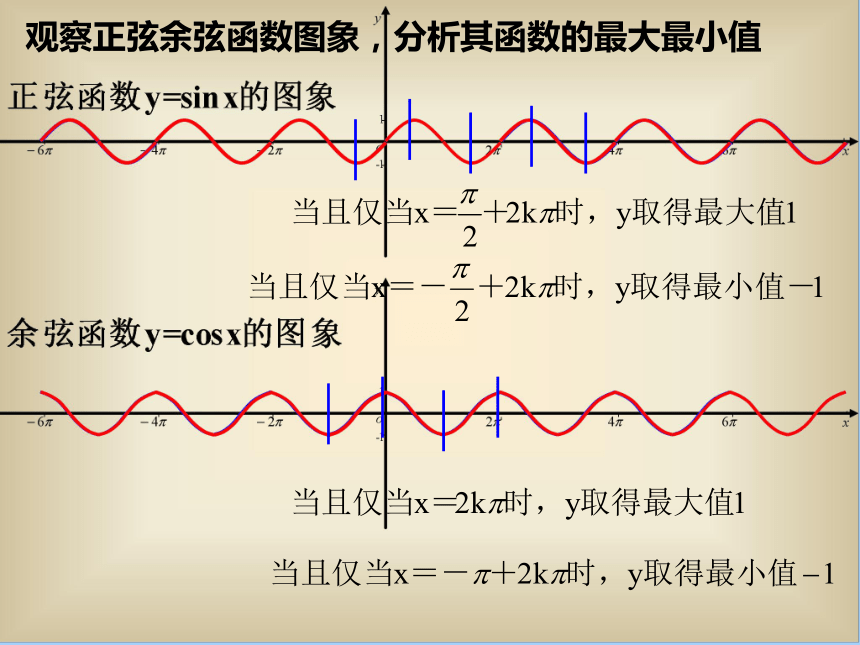
观察正弦余弦函数图象,分析其函数的最大最小值
例2. 求下列函数的单调区间:
(1) y=2sin(-x )
解:
y=2sin(-x )
= -2sinx
函数在 上单调递减
[ +2k , +2k ],k Z
函数在 上单调递增
[ +2k , +2k ],k Z
(2) y=3sin(2x- )
单调增区间为
所以:
解:
单调减区间为
例2 求下列函数的单调区间
解:
(4)
解:
定义域
(3)
y= ( tan )
sin2x
单调减区间为
单调增区间为
当
即
为减区间。
当
即
为增区间。
拓展延伸
例4 求下列函数的值域.
练习
小结
1、判断函数的单调性,可利用定义、可观察图象, 还可考虑复合函数的单调性。
2、利用函数的单调性判断三角函数值的大小
方法:可利用诱导公式将角转化到三 角函数的同一个单调区间内
小 结:
正弦、余弦函数的单调性
奇偶性
单调性(单调区间)
[ +2k , +2k ],k Z
单调递增
[ +2k , +2k ],k Z
单调递减
[ +2k , 2k ],k Z
单调递增
[2k , 2k + ], k Z
单调递减
函数
余弦函数
正弦函数
求函数的单调区间:
1. 直接利用相关性质
2. 复合函数的单调性
3. 利用图象寻找单调区间
定义域
图象
值域
奇偶性
对称性(对称轴、 对称中心)
周期性
R
R
[-1,1]
[-1,1]
奇
偶
X=kπ
-
-
-
-
-
-
-
-
(kπ,0)
知识回顾
-1 1
1 -1
-1 1
1 -1
观察正弦余弦函数图象,分析其函数的单调性
观察正弦余弦函数图象,分析其函数的最大最小值
例2. 求下列函数的单调区间:
(1) y=2sin(-x )
解:
y=2sin(-x )
= -2sinx
函数在 上单调递减
[ +2k , +2k ],k Z
函数在 上单调递增
[ +2k , +2k ],k Z
(2) y=3sin(2x- )
单调增区间为
所以:
解:
单调减区间为
例2 求下列函数的单调区间
解:
(4)
解:
定义域
(3)
y= ( tan )
sin2x
单调减区间为
单调增区间为
当
即
为减区间。
当
即
为增区间。
拓展延伸
例4 求下列函数的值域.
练习
小结
1、判断函数的单调性,可利用定义、可观察图象, 还可考虑复合函数的单调性。
2、利用函数的单调性判断三角函数值的大小
方法:可利用诱导公式将角转化到三 角函数的同一个单调区间内
小 结:
正弦、余弦函数的单调性
奇偶性
单调性(单调区间)
[ +2k , +2k ],k Z
单调递增
[ +2k , +2k ],k Z
单调递减
[ +2k , 2k ],k Z
单调递增
[2k , 2k + ], k Z
单调递减
函数
余弦函数
正弦函数
求函数的单调区间:
1. 直接利用相关性质
2. 复合函数的单调性
3. 利用图象寻找单调区间
