2.2.2 函数的减法运算及其几何意义 课件
文档属性
| 名称 | 2.2.2 函数的减法运算及其几何意义 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 485.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-08-15 16:09:37 | ||
图片预览









文档简介
(共56张PPT)
2.2.2向量减法运算
及其几何意义
复习回顾
1.向量加法的三角形法则
复习回顾
1.向量加法的三角形法则
2.向量加法的四边形法则
复习回顾
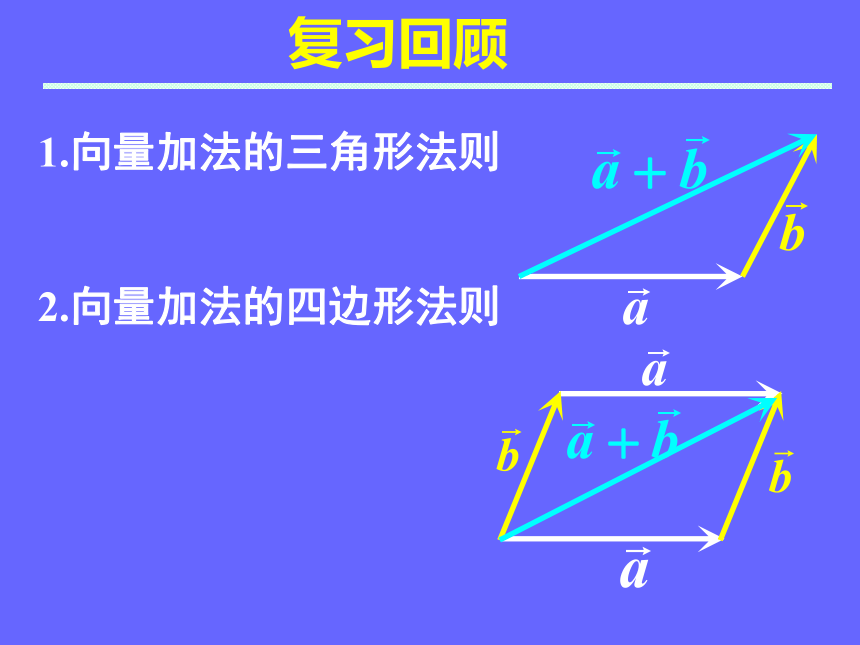
1.向量加法的三角形法则
2.向量加法的四边形法则
讲授新课
1. 向量是否有减法
探究
讲授新课
1. 向量是否有减法
2. 向量的减法是否与数的减法有类
似的法则
探究
讲授新课
1. 相反向量:
讲授新课
1. 相反向量:
讲授新课
1. 相反向量:
讲授新课
1. 相反向量:
讲授新课
1. 相反向量:
讲授新课
1. 相反向量:
讲授新课
2. 向量的减法:
讲授新课
2. 向量的减法:
讲授新课
2. 向量的减法:
讲授新课
2. 向量的减法:
思 考
讲授新课
2. 向量的减法:
思 考
讲授新课
A
B
C
2. 向量的减法:
讲授新课
A
B
C
分 析:
2. 向量的减法:
讲授新课
A
B
C
分 析:
2. 向量的减法:
讲授新课
A
B
C
分 析:
2. 向量的减法:
讲授新课
2. 向量的减法:
向量减法法则:
讲授新课
2. 向量的减法:
向量减法法则:
两向量起点相同,则差向量就是连结
两向量终点,指向被减向量终点的向量.
讲授新课
2. 向量的减法:
向量减法法则:
注 意:
两向量起点相同,则差向量就是连结
两向量终点,指向被减向量终点的向量.
(1)起点相同;
讲授新课
2. 向量的减法:
向量减法法则:
注 意:
两向量起点相同,则差向量就是连结
两向量终点,指向被减向量终点的向量.
(1)起点相同;
(2)指向被减向量的终点.
讲授新课
练习1.
(1)
讲授新课
练习1.
?
(1)
讲授新课
练习1.
?
(1)
讲授新课
练习1.
(2)
A
B
C
讲授新课
练习1.
(2)
A
B
C
讲授新课
练习1.
(3)
讲授新课
练习1.
(3)
讲授新课
练习1.
(3)
讲授新课
练习1.
(3)
讲授新课
练习1.
(3)
讲授新课
例1.
讲授新课
O
例1.
讲授新课
O
A
例1.
讲授新课
O
A
B
例1.
讲授新课
O
A
B
例1.
讲授新课
O
A
B
C
例1.
讲授新课
O
A
B
C
D
例1.
讲授新课
O
A
B
C
D
例1.
讲授新课
O
A
B
C
D
作法:
例1.
讲授新课
O
A
B
C
D
作法:
例1.
讲授新课
D
C
A
B
例2.
讲授新课
解:
D
C
A
B
例2.
讲授新课
解:
D
C
A
B
例2.
讲授新课
D
C
A
B
讲授新课
D
C
A
B
讲授新课
D
C
A
B
讲授新课
例3.
D
C
A
B
O
课堂小结
向量的减法的定义及向量减
法的三角形法则及运用.
阅读教材P.85-P.86;
《习案》作业十九.
课后作业
2.2.2向量减法运算
及其几何意义
复习回顾
1.向量加法的三角形法则
复习回顾
1.向量加法的三角形法则
2.向量加法的四边形法则
复习回顾
1.向量加法的三角形法则
2.向量加法的四边形法则
讲授新课
1. 向量是否有减法
探究
讲授新课
1. 向量是否有减法
2. 向量的减法是否与数的减法有类
似的法则
探究
讲授新课
1. 相反向量:
讲授新课
1. 相反向量:
讲授新课
1. 相反向量:
讲授新课
1. 相反向量:
讲授新课
1. 相反向量:
讲授新课
1. 相反向量:
讲授新课
2. 向量的减法:
讲授新课
2. 向量的减法:
讲授新课
2. 向量的减法:
讲授新课
2. 向量的减法:
思 考
讲授新课
2. 向量的减法:
思 考
讲授新课
A
B
C
2. 向量的减法:
讲授新课
A
B
C
分 析:
2. 向量的减法:
讲授新课
A
B
C
分 析:
2. 向量的减法:
讲授新课
A
B
C
分 析:
2. 向量的减法:
讲授新课
2. 向量的减法:
向量减法法则:
讲授新课
2. 向量的减法:
向量减法法则:
两向量起点相同,则差向量就是连结
两向量终点,指向被减向量终点的向量.
讲授新课
2. 向量的减法:
向量减法法则:
注 意:
两向量起点相同,则差向量就是连结
两向量终点,指向被减向量终点的向量.
(1)起点相同;
讲授新课
2. 向量的减法:
向量减法法则:
注 意:
两向量起点相同,则差向量就是连结
两向量终点,指向被减向量终点的向量.
(1)起点相同;
(2)指向被减向量的终点.
讲授新课
练习1.
(1)
讲授新课
练习1.
?
(1)
讲授新课
练习1.
?
(1)
讲授新课
练习1.
(2)
A
B
C
讲授新课
练习1.
(2)
A
B
C
讲授新课
练习1.
(3)
讲授新课
练习1.
(3)
讲授新课
练习1.
(3)
讲授新课
练习1.
(3)
讲授新课
练习1.
(3)
讲授新课
例1.
讲授新课
O
例1.
讲授新课
O
A
例1.
讲授新课
O
A
B
例1.
讲授新课
O
A
B
例1.
讲授新课
O
A
B
C
例1.
讲授新课
O
A
B
C
D
例1.
讲授新课
O
A
B
C
D
例1.
讲授新课
O
A
B
C
D
作法:
例1.
讲授新课
O
A
B
C
D
作法:
例1.
讲授新课
D
C
A
B
例2.
讲授新课
解:
D
C
A
B
例2.
讲授新课
解:
D
C
A
B
例2.
讲授新课
D
C
A
B
讲授新课
D
C
A
B
讲授新课
D
C
A
B
讲授新课
例3.
D
C
A
B
O
课堂小结
向量的减法的定义及向量减
法的三角形法则及运用.
阅读教材P.85-P.86;
《习案》作业十九.
课后作业
