苏科版七年级数学上册 6.3 余角、补角、对顶角(2)课件(18张PPT)
文档属性
| 名称 | 苏科版七年级数学上册 6.3 余角、补角、对顶角(2)课件(18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-16 21:20:13 | ||
图片预览



文档简介
(共18张PPT)
6.3 余角、补角、对顶角(2)
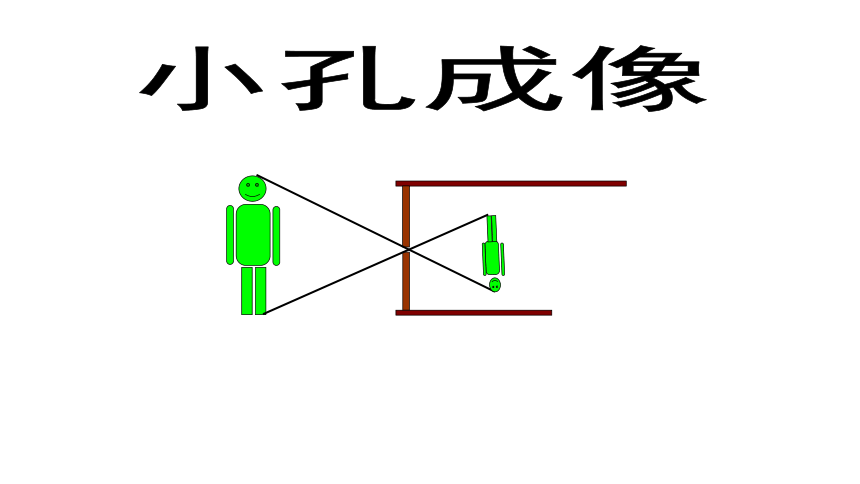
小孔成像
我国古代的墨子对光学很有研究,对光的直线传播、光的反射和物影成像,进行了精彩的描述。有一次墨子做了一个实验,他通过了小孔成像阐述了光的直线传播原理。这后来成了摄影技术的先声。
情境导学:
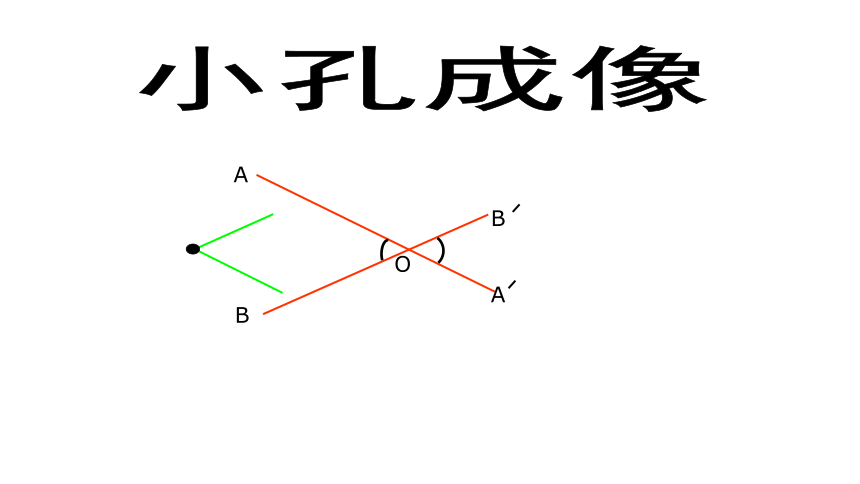
A
B
O
B
A
任务自学:
(一)目标呈现
1.在具体情境中了解对顶角,能够识别对顶角,并能理解对顶角的性质;
2.能正确地运用对顶角的性质解决问题。
(二)自主学习
自学课本第161页“读一读”-162页,完成以下问题:
师生品学:
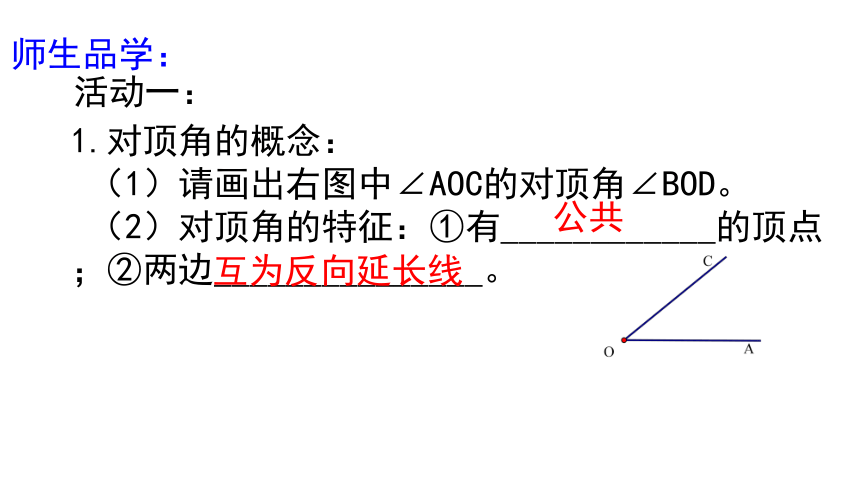
1.对顶角的概念:
(1)请画出右图中∠AOC的对顶角∠BOD。
(2)对顶角的特征:①有____________的顶点;②两边_______________。
公共
互为反向延长线
活动一:
2.下列各图中,∠1与∠2是对顶角是:______。
(2)(5)
3.如图,直线AB、CD、EF相交于点O,
(1)则∠AOE的对顶角是___,∠AOD的对顶角是___, ∠DOE的对顶角是 ,∠BOD的对顶角是____。
(2)图中两条直线AB、CD相交于点O,有 对对顶角。
(3)图中三条直线相交于同一点共有多少对对顶角?请分别把它们表示出来。
∠BOF
∠BOC
∠COF
∠COA
两
解:图中有6对对顶角,它们分别是∠AOC与∠BOD、 ∠AOD与∠BOC; ∠AOE与∠BOF、 ∠AOF与BOE; ∠COE与DOF、 ∠COF与∠DOE。
如图,将两根木条a、b钉在一起,并把它们看成两条相 交直线。如果∠1=50°,那么∠2、∠3、∠4各等于多少 度 由此,你发现了什么?
当∠1=50°时,∠2= ,∠3= ,∠4= 。
当∠1= 时,∠2= ,∠3= ,∠4= 。
发现:
对顶角的性质: 。
对顶角相等
活动二:
你能用学过的知识说明结论成立吗
理由:
∵∠1、∠3都是∠2的补角,
∴∠1=∠3.(同角的补角相等)
同样,可以得到∠2=∠4.
追问:你觉得相等的角是对顶角吗?
符号语言:
∵∠1与∠3,∠2与∠4是对顶角∴∠1=∠3,∠2=∠4(对顶角相等)
A
D
C
B
O
例:如图,直线AB、CD相交于点O,∠BOD与∠BOE
互为余角,∠AOC=72°,求∠BOE的度数。
变式:如图,直线AB、CD相交于点O,OE是∠BOC的角平分线,∠AOC=72°,求∠BOE的度数。
练习固学:
1.如图,直线AB、CD、EF相交于点O,∠AOF的对顶角是( )
A. ∠BCD B. ∠EOB C. ∠COE D. ∠AOC
B
2.如图,直线AB、CD相交于点E,∠AEF=90°,则(1)∠1和∠2为 角,∠1和∠3互为 角;
(2)若∠3=32°,则∠4= °
对顶
余
122
3.平面内相交于一点的四条直线构成的对顶角共有( )
A.5对 B.8对 C.10对 D.12对
D
4.如图,直线AB、CD相交于点O,OE平分∠BOD,∠AOC=72°,∠DOF=90°,求∠EOF的度数。
小结悟学:
1.对顶角的概念、性质.
2.对顶角的特征.
3.正确的说理过程,转化思想.
4.几何图形常见的研究方向:位置关系、数量关系.
作业:
必做作业:P.164习题第7、8、9
选做作业:
如图,直线CE、DF相交于点P
(1)当∠CPD=40°时,直接写出另外三个角的度数;
(2)当∠CPF=2∠EPF时,解答下面两道题:
①求∠DPE的度数;
②过点P作射线PQ,将∠DPE分成1:2两部分,求∠CPQ的度数
谢 谢!
6.3 余角、补角、对顶角(2)
小孔成像
我国古代的墨子对光学很有研究,对光的直线传播、光的反射和物影成像,进行了精彩的描述。有一次墨子做了一个实验,他通过了小孔成像阐述了光的直线传播原理。这后来成了摄影技术的先声。
情境导学:
A
B
O
B
A
任务自学:
(一)目标呈现
1.在具体情境中了解对顶角,能够识别对顶角,并能理解对顶角的性质;
2.能正确地运用对顶角的性质解决问题。
(二)自主学习
自学课本第161页“读一读”-162页,完成以下问题:
师生品学:
1.对顶角的概念:
(1)请画出右图中∠AOC的对顶角∠BOD。
(2)对顶角的特征:①有____________的顶点;②两边_______________。
公共
互为反向延长线
活动一:
2.下列各图中,∠1与∠2是对顶角是:______。
(2)(5)
3.如图,直线AB、CD、EF相交于点O,
(1)则∠AOE的对顶角是___,∠AOD的对顶角是___, ∠DOE的对顶角是 ,∠BOD的对顶角是____。
(2)图中两条直线AB、CD相交于点O,有 对对顶角。
(3)图中三条直线相交于同一点共有多少对对顶角?请分别把它们表示出来。
∠BOF
∠BOC
∠COF
∠COA
两
解:图中有6对对顶角,它们分别是∠AOC与∠BOD、 ∠AOD与∠BOC; ∠AOE与∠BOF、 ∠AOF与BOE; ∠COE与DOF、 ∠COF与∠DOE。
如图,将两根木条a、b钉在一起,并把它们看成两条相 交直线。如果∠1=50°,那么∠2、∠3、∠4各等于多少 度 由此,你发现了什么?
当∠1=50°时,∠2= ,∠3= ,∠4= 。
当∠1= 时,∠2= ,∠3= ,∠4= 。
发现:
对顶角的性质: 。
对顶角相等
活动二:
你能用学过的知识说明结论成立吗
理由:
∵∠1、∠3都是∠2的补角,
∴∠1=∠3.(同角的补角相等)
同样,可以得到∠2=∠4.
追问:你觉得相等的角是对顶角吗?
符号语言:
∵∠1与∠3,∠2与∠4是对顶角∴∠1=∠3,∠2=∠4(对顶角相等)
A
D
C
B
O
例:如图,直线AB、CD相交于点O,∠BOD与∠BOE
互为余角,∠AOC=72°,求∠BOE的度数。
变式:如图,直线AB、CD相交于点O,OE是∠BOC的角平分线,∠AOC=72°,求∠BOE的度数。
练习固学:
1.如图,直线AB、CD、EF相交于点O,∠AOF的对顶角是( )
A. ∠BCD B. ∠EOB C. ∠COE D. ∠AOC
B
2.如图,直线AB、CD相交于点E,∠AEF=90°,则(1)∠1和∠2为 角,∠1和∠3互为 角;
(2)若∠3=32°,则∠4= °
对顶
余
122
3.平面内相交于一点的四条直线构成的对顶角共有( )
A.5对 B.8对 C.10对 D.12对
D
4.如图,直线AB、CD相交于点O,OE平分∠BOD,∠AOC=72°,∠DOF=90°,求∠EOF的度数。
小结悟学:
1.对顶角的概念、性质.
2.对顶角的特征.
3.正确的说理过程,转化思想.
4.几何图形常见的研究方向:位置关系、数量关系.
作业:
必做作业:P.164习题第7、8、9
选做作业:
如图,直线CE、DF相交于点P
(1)当∠CPD=40°时,直接写出另外三个角的度数;
(2)当∠CPF=2∠EPF时,解答下面两道题:
①求∠DPE的度数;
②过点P作射线PQ,将∠DPE分成1:2两部分,求∠CPQ的度数
谢 谢!
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
