有理数乘方的意义
图片预览




文档简介
(共29张PPT)
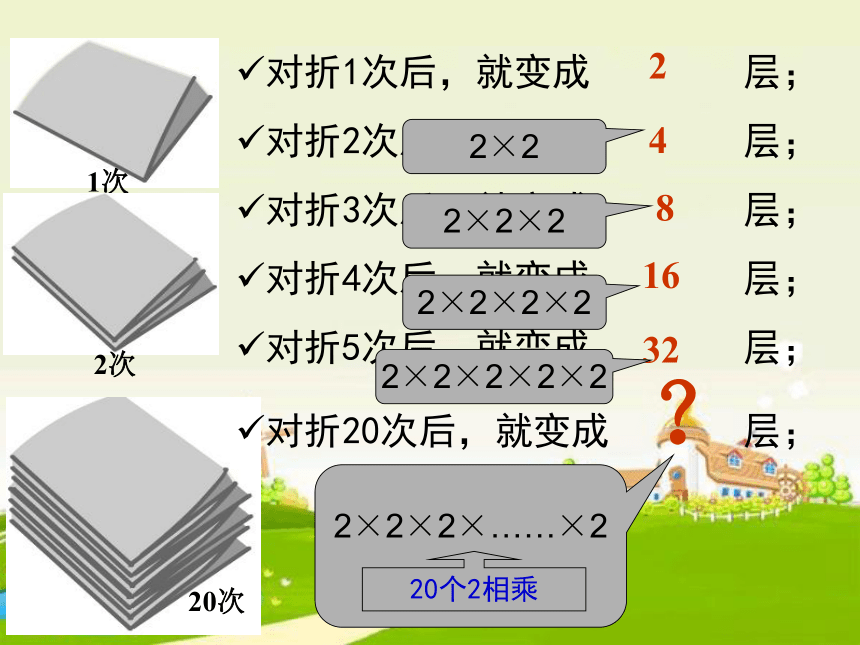
给你一张足够大的纸,对折20次,得到的高度可以超过高楼大厦。你信吗
对折1次后,就变成 层;
对折2次后,就变成 层;
对折3次后,就变成 层;
对折4次后,就变成 层;
对折5次后,就变成 层;
对折20次后,就变成 层;
2
1次
2次
20次
4
8
16
?
2×2
2×2×2
2×2×2×2
2×2×2×……×2
20个2相乘
32
2×2×2×2×2
有理数的乘方
the Involution of Rational Number
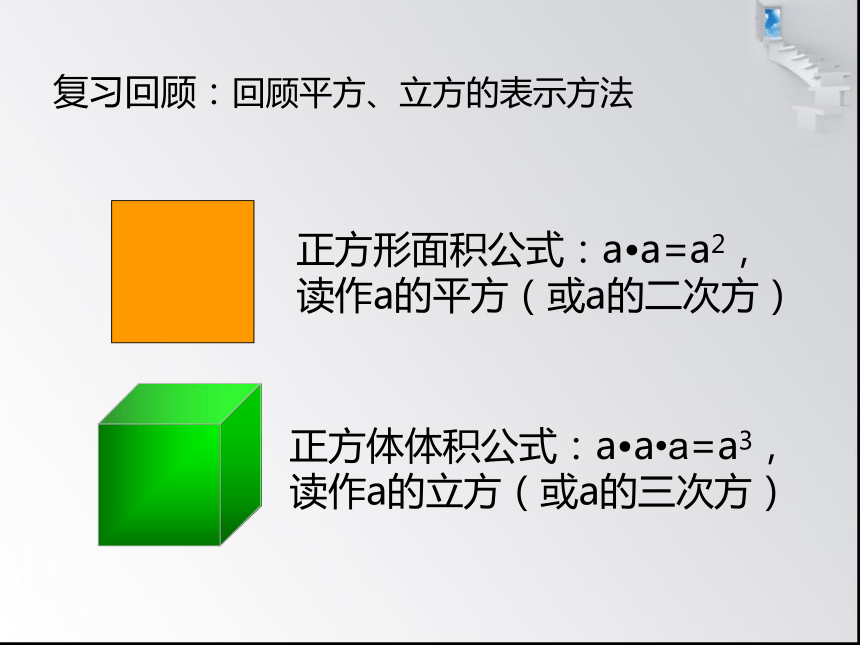
复习回顾:回顾平方、立方的表示方法
正方形面积公式:a a=a2,
读作a的平方(或a的二次方)
正方体体积公式:a a a=a3,
读作a的立方(或a的三次方)
折叠四次后的层数:2×2×2×2
折叠五次后的层数: 2×2×2×2×2
1.这两个式子有什么相同点
答:它们都是乘法,并且它们各自的因数都相同。
24
25
2.同学们想一想:这样的运算能像平方、立方那样简写吗?
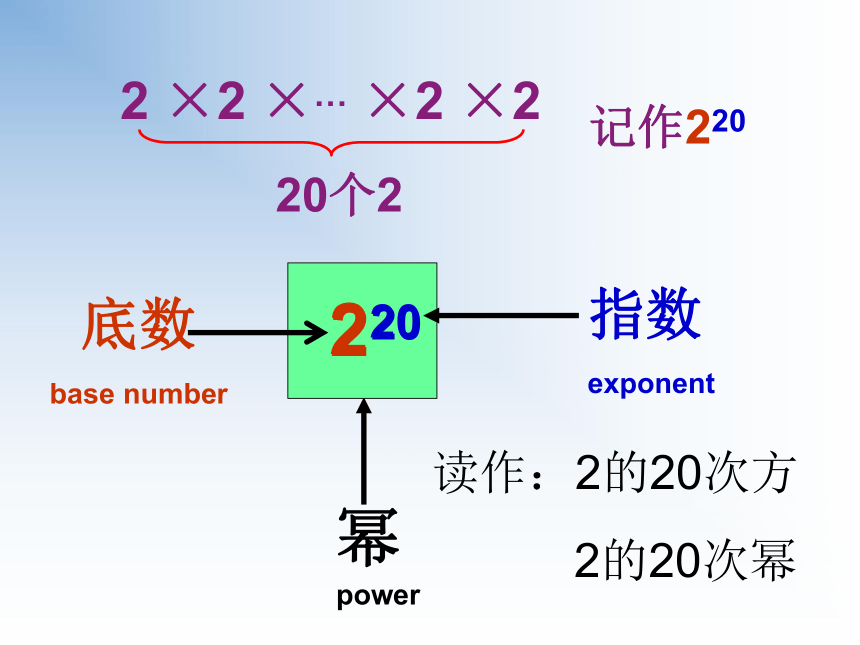
2 ×2 ×… ×2 ×2
20个2
记作220
读作:2的20次方
2的20次幂
幂
power
220
底数
base number
指数
exponent
2
20
3×3×3×3×3×3
(-7)×(-7)×(-7)×(-7)
1.5×1.5×1.5×1.5×1.5×1.5
把下列各式改写成乘方形式,并指明底数、指数各是什么:
36
(-7)4
1.56
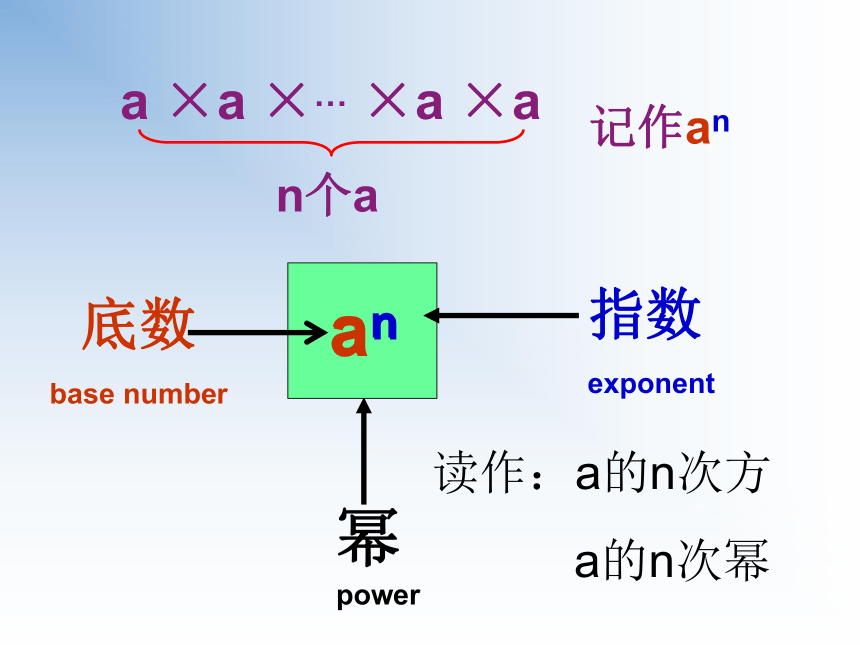
a ×a ×… ×a ×a
n个a
记作an
读作:a的n次方
a的n次幂
幂
power
an
底数
base number
指数
exponent
a
n
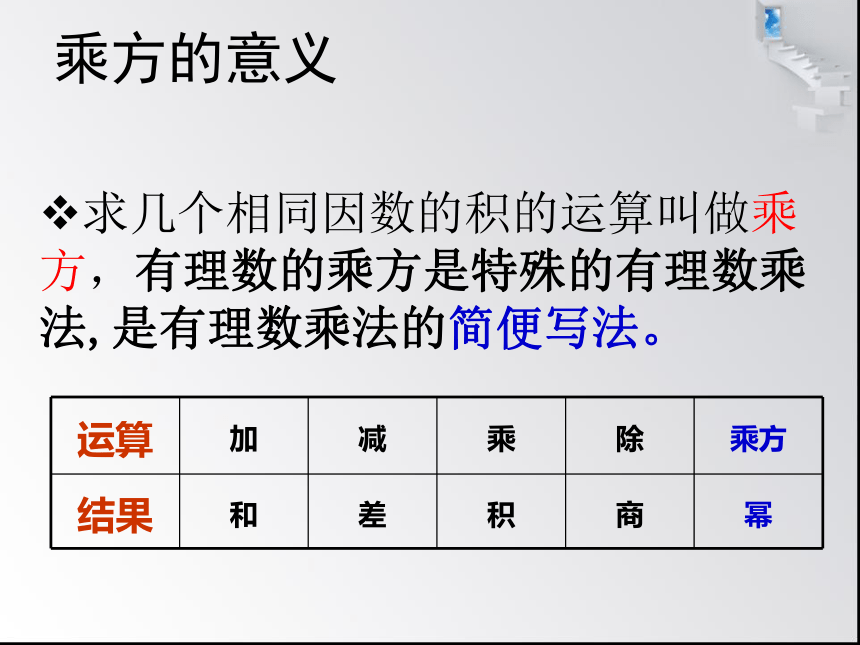
乘方的意义
求几个相同因数的积的运算叫做乘方,有理数的乘方是特殊的有理数乘法,是有理数乘法的简便写法。
运算 加 减 乘 除 乘方
结果 和 差 积 商 幂
(1)64中,底数是___,指数是____;
(3) 8中底数是 ___ ,指数是 ___ 。
写出下列各幂的底数与指数:
8
4
a
4
6
1
(2) a4中,底数是___,指数是____;
5
(4) 中,底数是____,指数是____;
一个数可以看作是这个数本身的一次方。
请你说说下列各数表示什么?它们一样吗?
(1) 23 , 32 , 3 ×2
对于分数的乘方,负数的乘方,书写时一定要注意小括号。
(3) (-5)4 与 -54
(2) 与
3×3×3×3×3×3
7×7×7×7
1.5×1.5×1.5×1.5×1.5×1.5
36
74
1.56
有理数乘方的运算
a×a×a···×a
n个a
an
=
a的n次方等于n个a相乘,因此可以利用有理数的乘法运算进行有理数乘方的运算。
现在让我们来算一下220等于多少?看谁算得又快又准!
1048576
220
=
一张纸厚度是多少?你怎么知道的?
一张纸不好测量,你手中有没有很多张纸呀,比如书,或者本。(积少成多,化零为整)
一张纸的厚度大约为0.1毫米
一层楼房的高度大约是3米,那么105米大约有几层楼高?
给你一张足够大的纸,对折20次,得到的高度是不是超过了高楼大厦?
1048576
220
=
104.8576m
104857.6mm
=
(35层)
由2到1048576,你想到什么?
勿以善小而不为,
勿以恶小而为之。
现在让我们来算一下(90%)5等于多少?看谁算得又快又准!
59.049%
(90%)5
=
60分:及格线 90分:引以为豪
学习过程:一环扣一环,以乘方为基准产生结果,而不是百分比的简单叠加
90%的态度,5天后,59分(不及格)
更多90%会怎样?
59%
(90%)5
≈
课堂小结及反思
这节课你学会了一种什么运算?你有何体会?
“乘方”精神:虽然是简简单单的重复,但结果却是惊人的。做人也要这样,脚踏实地,一步一个脚印,成功也会令你惊喜的。
作业:
这节课我学会了……想到了……(反思文章)
预习乘方运算的性质以及有理数混合运算
拓展:棋盘上的学问
古时候,在某个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋。为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求。大臣说:“陛下,请您在这张棋盘的第1个小格里,赏给我1粒米,在第2个小格里给2粒,第3小格给4粒,以后每一小格都比前一小格加一倍。请您把这样摆满棋盘上所有的64格的米粒,都赏给您的仆人吧!” “你真傻!就要这么一点米粒?!”国王哈哈大笑,大臣说:“就怕您的国库里没有这么多米!”
你认为国王的国库里有这么多米吗?
给你一张足够大的纸,对折20次,得到的高度可以超过高楼大厦。你信吗
对折1次后,就变成 层;
对折2次后,就变成 层;
对折3次后,就变成 层;
对折4次后,就变成 层;
对折5次后,就变成 层;
对折20次后,就变成 层;
2
1次
2次
20次
4
8
16
?
2×2
2×2×2
2×2×2×2
2×2×2×……×2
20个2相乘
32
2×2×2×2×2
有理数的乘方
the Involution of Rational Number
复习回顾:回顾平方、立方的表示方法
正方形面积公式:a a=a2,
读作a的平方(或a的二次方)
正方体体积公式:a a a=a3,
读作a的立方(或a的三次方)
折叠四次后的层数:2×2×2×2
折叠五次后的层数: 2×2×2×2×2
1.这两个式子有什么相同点
答:它们都是乘法,并且它们各自的因数都相同。
24
25
2.同学们想一想:这样的运算能像平方、立方那样简写吗?
2 ×2 ×… ×2 ×2
20个2
记作220
读作:2的20次方
2的20次幂
幂
power
220
底数
base number
指数
exponent
2
20
3×3×3×3×3×3
(-7)×(-7)×(-7)×(-7)
1.5×1.5×1.5×1.5×1.5×1.5
把下列各式改写成乘方形式,并指明底数、指数各是什么:
36
(-7)4
1.56
a ×a ×… ×a ×a
n个a
记作an
读作:a的n次方
a的n次幂
幂
power
an
底数
base number
指数
exponent
a
n
乘方的意义
求几个相同因数的积的运算叫做乘方,有理数的乘方是特殊的有理数乘法,是有理数乘法的简便写法。
运算 加 减 乘 除 乘方
结果 和 差 积 商 幂
(1)64中,底数是___,指数是____;
(3) 8中底数是 ___ ,指数是 ___ 。
写出下列各幂的底数与指数:
8
4
a
4
6
1
(2) a4中,底数是___,指数是____;
5
(4) 中,底数是____,指数是____;
一个数可以看作是这个数本身的一次方。
请你说说下列各数表示什么?它们一样吗?
(1) 23 , 32 , 3 ×2
对于分数的乘方,负数的乘方,书写时一定要注意小括号。
(3) (-5)4 与 -54
(2) 与
3×3×3×3×3×3
7×7×7×7
1.5×1.5×1.5×1.5×1.5×1.5
36
74
1.56
有理数乘方的运算
a×a×a···×a
n个a
an
=
a的n次方等于n个a相乘,因此可以利用有理数的乘法运算进行有理数乘方的运算。
现在让我们来算一下220等于多少?看谁算得又快又准!
1048576
220
=
一张纸厚度是多少?你怎么知道的?
一张纸不好测量,你手中有没有很多张纸呀,比如书,或者本。(积少成多,化零为整)
一张纸的厚度大约为0.1毫米
一层楼房的高度大约是3米,那么105米大约有几层楼高?
给你一张足够大的纸,对折20次,得到的高度是不是超过了高楼大厦?
1048576
220
=
104.8576m
104857.6mm
=
(35层)
由2到1048576,你想到什么?
勿以善小而不为,
勿以恶小而为之。
现在让我们来算一下(90%)5等于多少?看谁算得又快又准!
59.049%
(90%)5
=
60分:及格线 90分:引以为豪
学习过程:一环扣一环,以乘方为基准产生结果,而不是百分比的简单叠加
90%的态度,5天后,59分(不及格)
更多90%会怎样?
59%
(90%)5
≈
课堂小结及反思
这节课你学会了一种什么运算?你有何体会?
“乘方”精神:虽然是简简单单的重复,但结果却是惊人的。做人也要这样,脚踏实地,一步一个脚印,成功也会令你惊喜的。
作业:
这节课我学会了……想到了……(反思文章)
预习乘方运算的性质以及有理数混合运算
拓展:棋盘上的学问
古时候,在某个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋。为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求。大臣说:“陛下,请您在这张棋盘的第1个小格里,赏给我1粒米,在第2个小格里给2粒,第3小格给4粒,以后每一小格都比前一小格加一倍。请您把这样摆满棋盘上所有的64格的米粒,都赏给您的仆人吧!” “你真傻!就要这么一点米粒?!”国王哈哈大笑,大臣说:“就怕您的国库里没有这么多米!”
你认为国王的国库里有这么多米吗?
