数学选修Ⅴ北师大版3.3基本不等式精品课件
文档属性
| 名称 | 数学选修Ⅴ北师大版3.3基本不等式精品课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 516.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-08-15 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
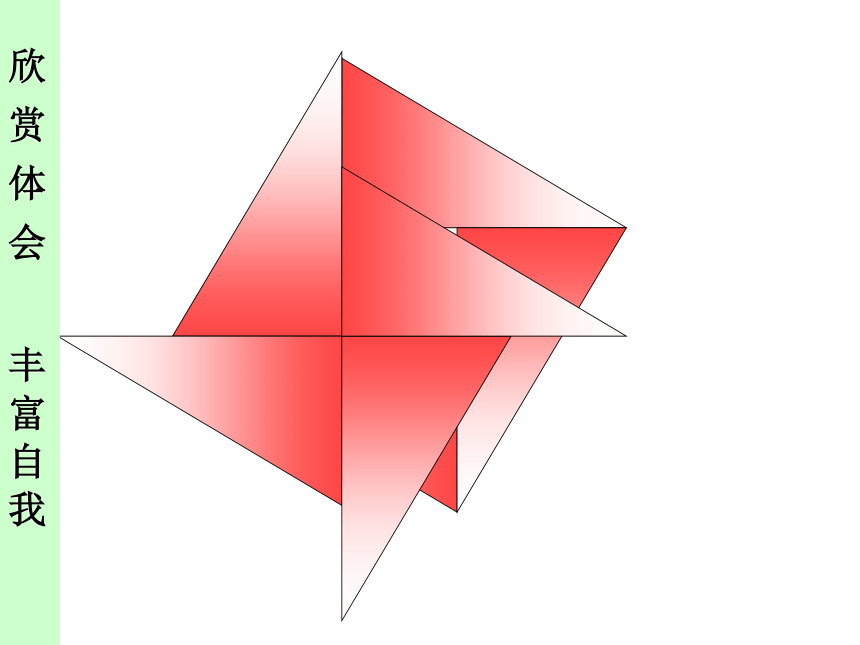
2002年国际数学家大会会标
欣 赏 体 会 丰 富 自 我
如图,这是在北京召开的第24届国际数学家大会会标.会标根据中国古代数学家赵爽的弦图设计的,颜色的明暗使它看上去象一个风车,代表中国人民热情好客。
欣 赏 体 会 丰 富 自 我
欣 赏 体 会 丰 富 自 我
探究1算一算?
数 学 是 思 维 的 体 操
a
b
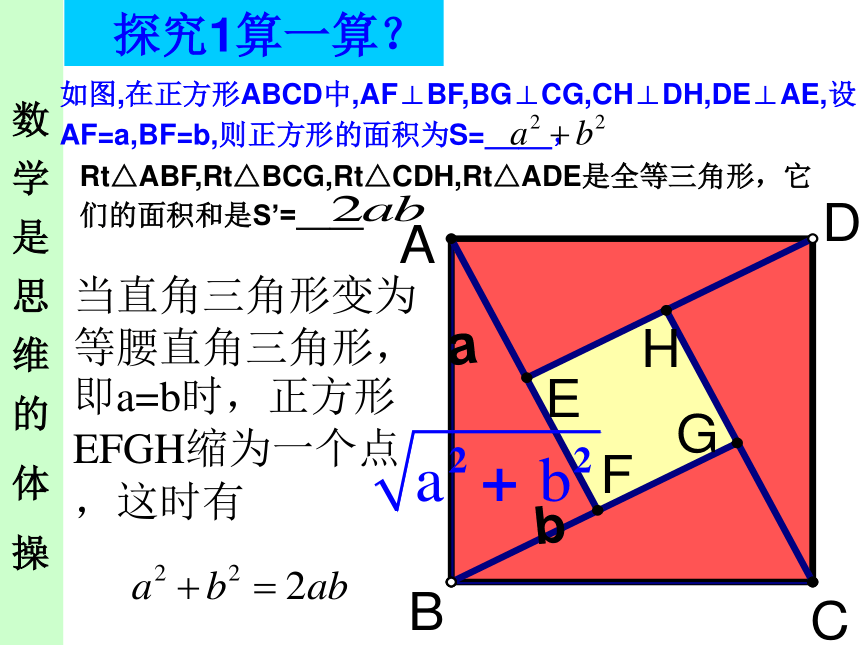
Rt△ABF,Rt△BCG,Rt△CDH,Rt△ADE是全等三角形,它们的面积和是S’=__
如图,在正方形ABCD中,AF⊥BF,BG⊥CG,CH⊥DH,DE⊥AE,设AF=a,BF=b,则正方形的面积为S=__,
当直角三角形变为等腰直角三角形,即a=b时,正方形EFGH缩为一个点,这时有
数 学 是 思 维 的 体 操
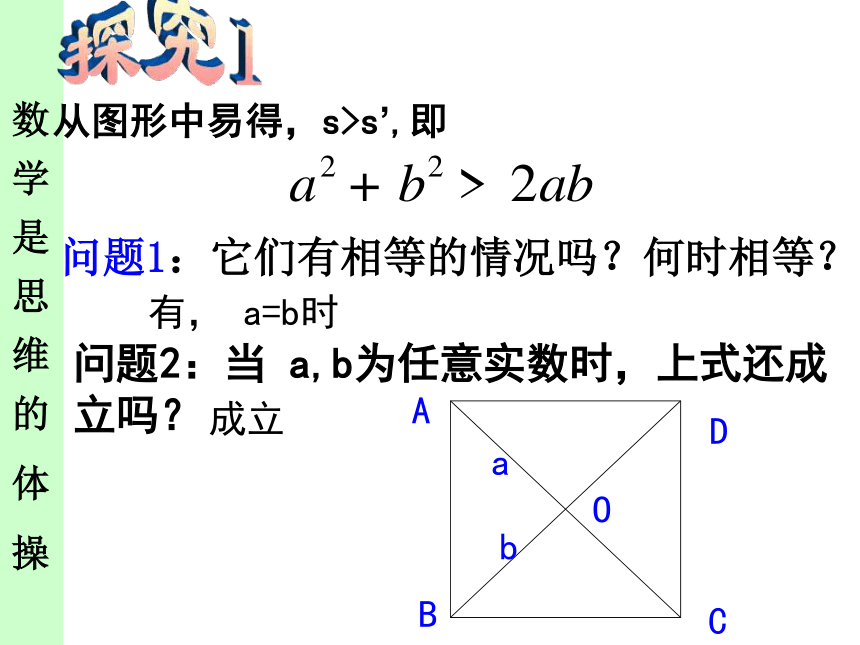
从图形中易得,s>s’,即
问题1:它们有相等的情况吗?何时相等?
问题2:当 a,b为任意实数时,上式还成 立吗?
有, a=b时
成立
a
b
A
B
C
D
O
一般地,对于任意实数a、b,我们有
当且仅当a=b时,等号成立
数 学 是 思 维 的 体 操
类 比 联 想 推 理 论 证
问题2
如果当 a>0 ,b>0 时,
用 分别代替a,b,可得,
探究2?
能不能证明
作差法
概 念 是 基 础 思 想 是 灵 魂
算术平均数
几何平均数
均值不等式
P89阅读材料
剖析公式应用
两个正数的算术平均数不小于它们的几何平均数.
⑴ a、 b是两个正数.
⑵ 当且仅当a=b时“=”号成立 ’
2.正用、逆用,注意成立的条件
3.变形用
1. 基本不等式可以叙述为:
深 入 探 究 揭 示 本 质
4.基本不等式可叙述为:两个正数的算术平均数不小于它们的几何平均数。
数 学 是 思 维 的 体 操
探究3?
如图,AB是圆的直径,C是AB上任一点,AC=a,CB=b,过点C作垂直于AB的弦DE,连AD,BD,
则CD=__, OD为__
你能用这个图得出基本不等式的几何解释吗
A
B
C
D
E
O
在同一圆中,半径不小于半弦
由图知OD≥CD
即有
≥
如图,AB是圆的直径,C是AB上任一点,AC=a,CB=b,过点C作垂直于AB的弦DF,连AD,BD,过C做CE⊥OD交OD与E,
则DC=__, DE为__由图知DC≥DE,则有
学 以 致 用
A
B
C
D
F
O
E
探究4?
∟
能不能证明
学 以 致 用
例题讲解
思 考 交 流
请同学们阅读P89思考交流,
利用FC≥OF得出一个关于a,b的不等式.
A
F
B
O
C
a
b
如图,AB是圆的直径,C是AB上任一点,AC=a,CB=b,OF⊥AB交上半圆于F,
则FC=__, OF为__
由FC ≥ OF可得 ≥
小结
你会了吗?
1.本节课主要学习了基本不等式的推导与初步应用。
巅 峰 回 眸 豁 然 开 朗
2.注意公式的正用、逆用、变形使用。
巅 峰 回 眸 豁 然 开 朗
(1)一般地,对于任意实数a、b,我们有
3.不等式
(2)当a>0,b>0时,有
上述四个不等式当且仅当a=b时,等号成立
(3)当a>0,b>0时,有
(4)当a>0,b>0时,有
由此可得
1.课本第94页习题3.3 A组第 3题。
P95B组 1.
跳 起 来 摘 下 丰 收 果
2.弹性作业:是否还有其他证明不等式
(
的方法和几何解释
和
2002年国际数学家大会会标
欣 赏 体 会 丰 富 自 我
如图,这是在北京召开的第24届国际数学家大会会标.会标根据中国古代数学家赵爽的弦图设计的,颜色的明暗使它看上去象一个风车,代表中国人民热情好客。
欣 赏 体 会 丰 富 自 我
欣 赏 体 会 丰 富 自 我
探究1算一算?
数 学 是 思 维 的 体 操
a
b
Rt△ABF,Rt△BCG,Rt△CDH,Rt△ADE是全等三角形,它们的面积和是S’=__
如图,在正方形ABCD中,AF⊥BF,BG⊥CG,CH⊥DH,DE⊥AE,设AF=a,BF=b,则正方形的面积为S=__,
当直角三角形变为等腰直角三角形,即a=b时,正方形EFGH缩为一个点,这时有
数 学 是 思 维 的 体 操
从图形中易得,s>s’,即
问题1:它们有相等的情况吗?何时相等?
问题2:当 a,b为任意实数时,上式还成 立吗?
有, a=b时
成立
a
b
A
B
C
D
O
一般地,对于任意实数a、b,我们有
当且仅当a=b时,等号成立
数 学 是 思 维 的 体 操
类 比 联 想 推 理 论 证
问题2
如果当 a>0 ,b>0 时,
用 分别代替a,b,可得,
探究2?
能不能证明
作差法
概 念 是 基 础 思 想 是 灵 魂
算术平均数
几何平均数
均值不等式
P89阅读材料
剖析公式应用
两个正数的算术平均数不小于它们的几何平均数.
⑴ a、 b是两个正数.
⑵ 当且仅当a=b时“=”号成立 ’
2.正用、逆用,注意成立的条件
3.变形用
1. 基本不等式可以叙述为:
深 入 探 究 揭 示 本 质
4.基本不等式可叙述为:两个正数的算术平均数不小于它们的几何平均数。
数 学 是 思 维 的 体 操
探究3?
如图,AB是圆的直径,C是AB上任一点,AC=a,CB=b,过点C作垂直于AB的弦DE,连AD,BD,
则CD=__, OD为__
你能用这个图得出基本不等式的几何解释吗
A
B
C
D
E
O
在同一圆中,半径不小于半弦
由图知OD≥CD
即有
≥
如图,AB是圆的直径,C是AB上任一点,AC=a,CB=b,过点C作垂直于AB的弦DF,连AD,BD,过C做CE⊥OD交OD与E,
则DC=__, DE为__由图知DC≥DE,则有
学 以 致 用
A
B
C
D
F
O
E
探究4?
∟
能不能证明
学 以 致 用
例题讲解
思 考 交 流
请同学们阅读P89思考交流,
利用FC≥OF得出一个关于a,b的不等式.
A
F
B
O
C
a
b
如图,AB是圆的直径,C是AB上任一点,AC=a,CB=b,OF⊥AB交上半圆于F,
则FC=__, OF为__
由FC ≥ OF可得 ≥
小结
你会了吗?
1.本节课主要学习了基本不等式的推导与初步应用。
巅 峰 回 眸 豁 然 开 朗
2.注意公式的正用、逆用、变形使用。
巅 峰 回 眸 豁 然 开 朗
(1)一般地,对于任意实数a、b,我们有
3.不等式
(2)当a>0,b>0时,有
上述四个不等式当且仅当a=b时,等号成立
(3)当a>0,b>0时,有
(4)当a>0,b>0时,有
由此可得
1.课本第94页习题3.3 A组第 3题。
P95B组 1.
跳 起 来 摘 下 丰 收 果
2.弹性作业:是否还有其他证明不等式
(
的方法和几何解释
和
