2021秋北师版九下数学1.5.1方位角问题导学案(有答案)
文档属性
| 名称 | 2021秋北师版九下数学1.5.1方位角问题导学案(有答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 127.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-16 14:16:37 | ||
图片预览

文档简介
2021秋北师版九下数学1.5.1方位角问题导学案
1.理解航海方位角的概念,并学会画航行方位图,将航海问题转化成数学问题.
2.通过航海问题的解决让学生体会船只在海上航行的实际情景,从而培养空间想象力.
学会画航行的方位图,将航海问题转化成数学问题.
将航海的实际情景用航行方位图表现出来.
一、创设情景 明确目标
(1)回顾直角三角形边与角之间的关系.
(2)让学生画出方位角的示意图,并给出定义.
学生画图:
二、自主学习 指向目标
阅读教材第19页图1-13有关的内容,并完成《名师学案》中的“课前预习”部分.
三、合作探究 达成目标
方位角的实际问题
活动:出示幻灯片动画,动画内容如下:
一渔船以20海里/小时的速度跟踪鱼群由西向东航行,在A处测得灯塔C在北偏东60°方向上,继续航行1小时到达B点,这时测得灯塔C在北偏东30°方向上,已知灯塔C的周围10海里范围内有暗礁,如果渔船不改变航线继续向东航行,有没有触礁的危险?
展示点评:根据题中船的路径可以把它画成平面图,如图所示,根据实际问题,作CD⊥AD,在Rt△ACD中,求出CD的长度,然后比较CD与10海里的大小就可以确定此船有没有触礁的危险.
解答如下:
根据题意可知,∠BAC=30°,∠CBD=60°,
AB=20×1=20(海里).
则∠BAC=∠ACB=30°,
故AB=BC=20海里.
在直角三角形CBD中,
∵sin60°=CD∶CB=,
∴CD=20×=10>10
所以,货轮继续向东航行途中没有触礁的危险.
反思小结:(1)在这种航海问题上,首先通过方位角的定位画出平面示意图,用辅助线的方法把实际问题转化成数学问题(解直角三角形)
(2)方位角的位置要精确.
四、总结梳理 内化目标
本节课我们学习了航海方位角的概念,并学会根据航海实际情景来画航行方位图,将航海问题转化成数学问题来解决.
五.达标测试
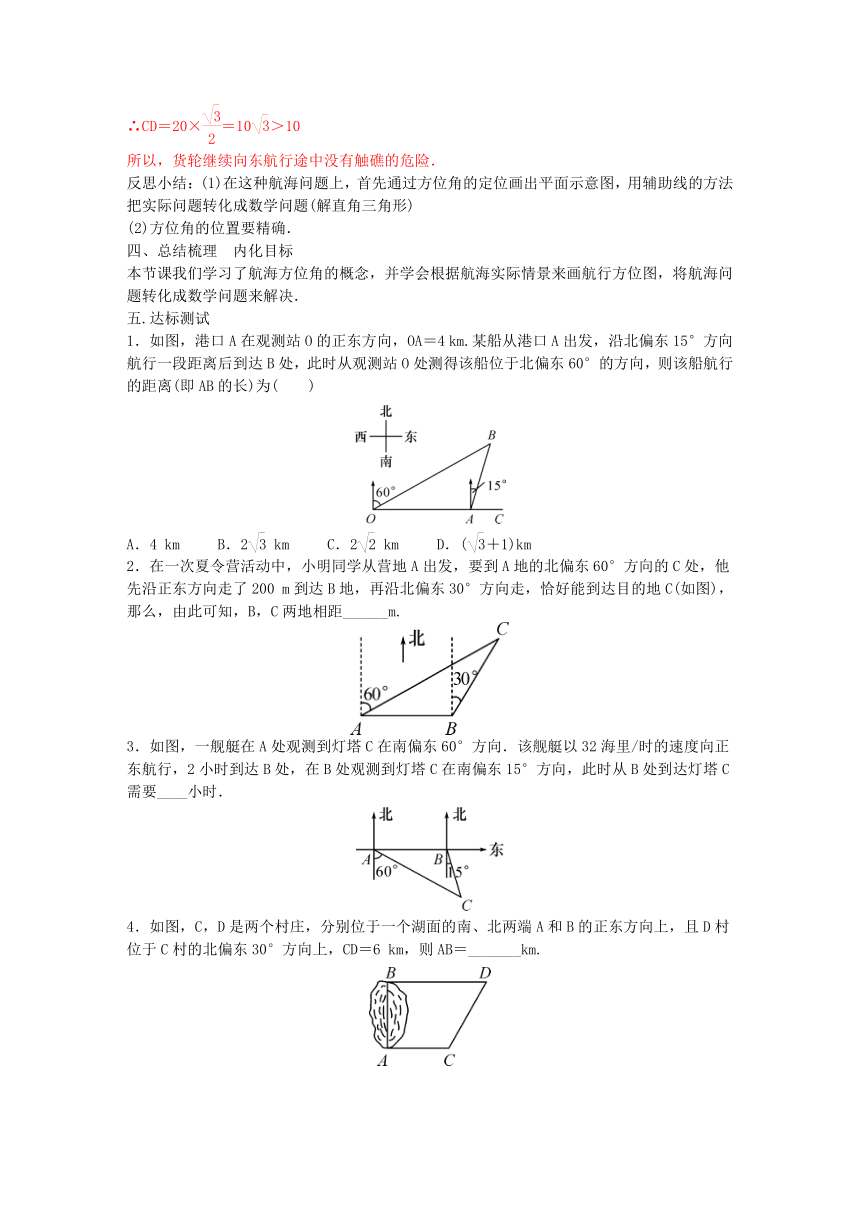
1.如图,港口A在观测站O的正东方向,OA=4 km.某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )
A.4 km B.2 km C.2 km D.(+1)km
2.在一次夏令营活动中,小明同学从营地A出发,要到A地的北偏东60°方向的C处,他先沿正东方向走了200 m到达B地,再沿北偏东30°方向走,恰好能到达目的地C(如图),那么,由此可知,B,C两地相距______m.
3.如图,一舰艇在A处观测到灯塔C在南偏东60°方向.该舰艇以32海里/时的速度向正东航行,2小时到达B处,在B处观测到灯塔C在南偏东15°方向,此时从B处到达灯塔C需要____小时.
4.如图,C,D是两个村庄,分别位于一个湖面的南、北两端A和B的正东方向上,且D村位于C村的北偏东30°方向上,CD=6 km,则AB=_______km.
5.如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达所在的B处距离灯塔P有多远?(结果用非特殊角的三角函数及根式表示即可)
6.如图,台风中心位于点P,并沿东北方向PQ移动,已知台风移动的速度为30千米/时,受影响区域的半径为200千米,B市位于点P的北偏东75°方向上,距离点P320千米处.
(1)说明本次台风会影响B市;
(2)求这次台风影响B市的时间.
达标测试答案
1. C
2. 200
3.
4. 3
5. 解:过点P作PD⊥AB于点D,由题意知∠DPB=45°,
在Rt△PBD中,sin45°=,∴PB=PD.
∵点A在P的北偏东65°方向,∠APD=25°,在Rt△PAD中,cos25°=,
∴PD=PAcos25°=80cos25°,
∴PB=80cos25°.
6. 解:(1)作BH⊥PQ于点H,在Rt△BHP中,由条件可知PB=320(千米),∠BPQ=30°,
得BH=320×sin30°=160<200,
∴本次台风会影响B市;
(2)如图,若台风中心移动到P1时,台风开始影响B市,台风中心移动到P2时,台风影响结束,由(1)得BH=160(千米).
由条件得BP1=BP2=200(千米),
∴P1P2=2=240(千米).
台风影响B市的时间t==8(小时).
1.理解航海方位角的概念,并学会画航行方位图,将航海问题转化成数学问题.
2.通过航海问题的解决让学生体会船只在海上航行的实际情景,从而培养空间想象力.
学会画航行的方位图,将航海问题转化成数学问题.
将航海的实际情景用航行方位图表现出来.
一、创设情景 明确目标
(1)回顾直角三角形边与角之间的关系.
(2)让学生画出方位角的示意图,并给出定义.
学生画图:
二、自主学习 指向目标
阅读教材第19页图1-13有关的内容,并完成《名师学案》中的“课前预习”部分.
三、合作探究 达成目标
方位角的实际问题
活动:出示幻灯片动画,动画内容如下:
一渔船以20海里/小时的速度跟踪鱼群由西向东航行,在A处测得灯塔C在北偏东60°方向上,继续航行1小时到达B点,这时测得灯塔C在北偏东30°方向上,已知灯塔C的周围10海里范围内有暗礁,如果渔船不改变航线继续向东航行,有没有触礁的危险?
展示点评:根据题中船的路径可以把它画成平面图,如图所示,根据实际问题,作CD⊥AD,在Rt△ACD中,求出CD的长度,然后比较CD与10海里的大小就可以确定此船有没有触礁的危险.
解答如下:
根据题意可知,∠BAC=30°,∠CBD=60°,
AB=20×1=20(海里).
则∠BAC=∠ACB=30°,
故AB=BC=20海里.
在直角三角形CBD中,
∵sin60°=CD∶CB=,
∴CD=20×=10>10
所以,货轮继续向东航行途中没有触礁的危险.
反思小结:(1)在这种航海问题上,首先通过方位角的定位画出平面示意图,用辅助线的方法把实际问题转化成数学问题(解直角三角形)
(2)方位角的位置要精确.
四、总结梳理 内化目标
本节课我们学习了航海方位角的概念,并学会根据航海实际情景来画航行方位图,将航海问题转化成数学问题来解决.
五.达标测试
1.如图,港口A在观测站O的正东方向,OA=4 km.某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )
A.4 km B.2 km C.2 km D.(+1)km
2.在一次夏令营活动中,小明同学从营地A出发,要到A地的北偏东60°方向的C处,他先沿正东方向走了200 m到达B地,再沿北偏东30°方向走,恰好能到达目的地C(如图),那么,由此可知,B,C两地相距______m.
3.如图,一舰艇在A处观测到灯塔C在南偏东60°方向.该舰艇以32海里/时的速度向正东航行,2小时到达B处,在B处观测到灯塔C在南偏东15°方向,此时从B处到达灯塔C需要____小时.
4.如图,C,D是两个村庄,分别位于一个湖面的南、北两端A和B的正东方向上,且D村位于C村的北偏东30°方向上,CD=6 km,则AB=_______km.
5.如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达所在的B处距离灯塔P有多远?(结果用非特殊角的三角函数及根式表示即可)
6.如图,台风中心位于点P,并沿东北方向PQ移动,已知台风移动的速度为30千米/时,受影响区域的半径为200千米,B市位于点P的北偏东75°方向上,距离点P320千米处.
(1)说明本次台风会影响B市;
(2)求这次台风影响B市的时间.
达标测试答案
1. C
2. 200
3.
4. 3
5. 解:过点P作PD⊥AB于点D,由题意知∠DPB=45°,
在Rt△PBD中,sin45°=,∴PB=PD.
∵点A在P的北偏东65°方向,∠APD=25°,在Rt△PAD中,cos25°=,
∴PD=PAcos25°=80cos25°,
∴PB=80cos25°.
6. 解:(1)作BH⊥PQ于点H,在Rt△BHP中,由条件可知PB=320(千米),∠BPQ=30°,
得BH=320×sin30°=160<200,
∴本次台风会影响B市;
(2)如图,若台风中心移动到P1时,台风开始影响B市,台风中心移动到P2时,台风影响结束,由(1)得BH=160(千米).
由条件得BP1=BP2=200(千米),
∴P1P2=2=240(千米).
台风影响B市的时间t==8(小时).
