2021-2022学年安徽省宣城六中八年级(上)开学数学试卷(word解析版)
文档属性
| 名称 | 2021-2022学年安徽省宣城六中八年级(上)开学数学试卷(word解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 211.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-17 08:20:43 | ||
图片预览



文档简介
2021-2022学年安徽省宣城六中八年级(上)开学数学试卷
一、选择题(本大题共10小题,共30分)
1.(3分)4的平方根是( )
A.2 B.﹣2 C.±2 D.
2.(3分)若(x2+px+q)(x﹣2)展开后不含x的一次项,则p与q的关系是( )
A.p=2q B.q=2p C.p+2q=0 D.q+2p=0
3.(3分)若实数x和y满足x>y,则下列式子中错误的是( )
A.2x﹣6>2y﹣6 B.x+1>y+1 C.﹣3x>﹣3y D.﹣<﹣
4.(3分)计算﹣3xy所得的结果为( )
A.﹣2y3 B.﹣2y C.﹣ D.﹣22y3
5.(3分)如图,一把矩形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,则∠DBC的度数为( )
A.55° B.65° C.75° D.125°
6.(3分)在平面直角坐标系中,点P(﹣2,1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.(3分)若关于x的方程﹣2x+b=0的解为x=2,则直线y=﹣2x+b一定经过点( )
A.(2,0) B.(0,3) C.(4,0) D.(2,5)
8.(3分)已知一次函数y=kx﹣3的图象经过点P,且y随x的增大而增大,则点P的坐标可以是( )
A.(﹣1,﹣2) B.(﹣2,﹣3) C.(1,﹣4) D.(2,﹣2)
9.(3分)若一个三角形的三个内角度数的比为2:3:4,则这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
10.(3分)等腰三角形一边的长为4cm,周长是18cm,则底边的长是( )
A.4cm B.10cm C.7或10cm D.4或10cm
二、填空题(本大题共6小题,共18分)
11.(3分)比较大小: .
12.(3分)分解因式:3x2﹣3y2= .
13.(3分)若a2+4ab﹣b2=0,则﹣= .
14.(3分)函数y=的自变量x的取值范围是 .
15.(3分)已知实数a、b、c满足a+b=ab=c,有下列结论:
①若a=3,则b+c=9;
②若a=b=c,则abc=0;
③若c≠0,则+=1;
④若a、b、c中只有两个数相等,则a+b+c=8.
其中正确的是 (把所有正确结论的序号都选上).
16.(3分)小李以每千克0.8元的价格从批发市场购进若干千克西瓜到市场去销售,在销售了部分西瓜之后,余下的每千克降价0.4元;销售金额与卖瓜千克数之间的关系如图所示,那么小李赚了 元.
三、解答题(本大题共7小题,共52分)
17.(6分)计算:.
18.(6分)解不等式组:,并把解集在数轴上表示出来.
19.(8分)已知实数m,n满足m+n=6,mn=﹣3.
(1)求(m﹣2)(n﹣2)的值;
(2)求m2+n2的值.
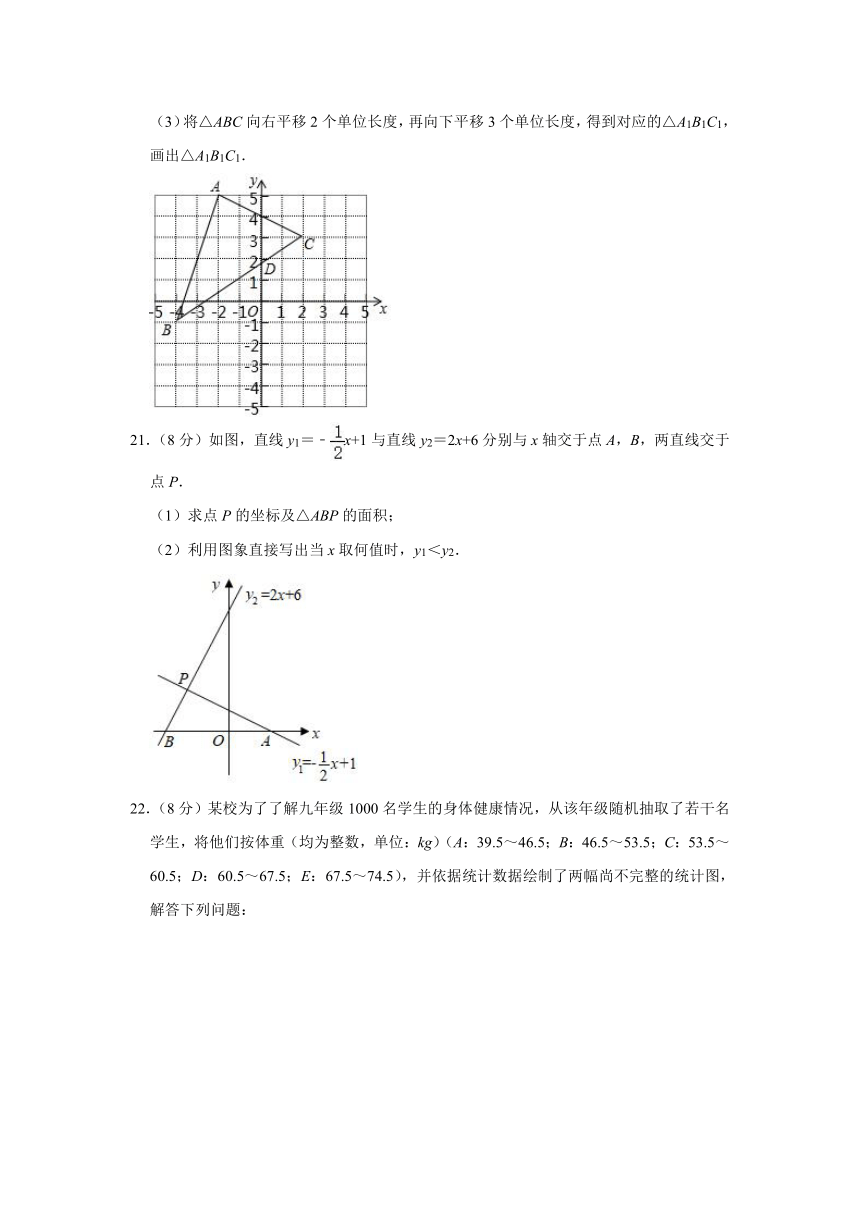
20.(8分)如图.
(1)写出点A,B,C的坐标;
(2)求S△ABC;
(3)将△ABC向右平移2个单位长度,再向下平移3个单位长度,得到对应的△A1B1C1,画出△A1B1C1.
21.(8分)如图,直线y1=﹣x+1与直线y2=2x+6分别与x轴交于点A,B,两直线交于点P.
(1)求点P的坐标及△ABP的面积;
(2)利用图象直接写出当x取何值时,y1<y2.
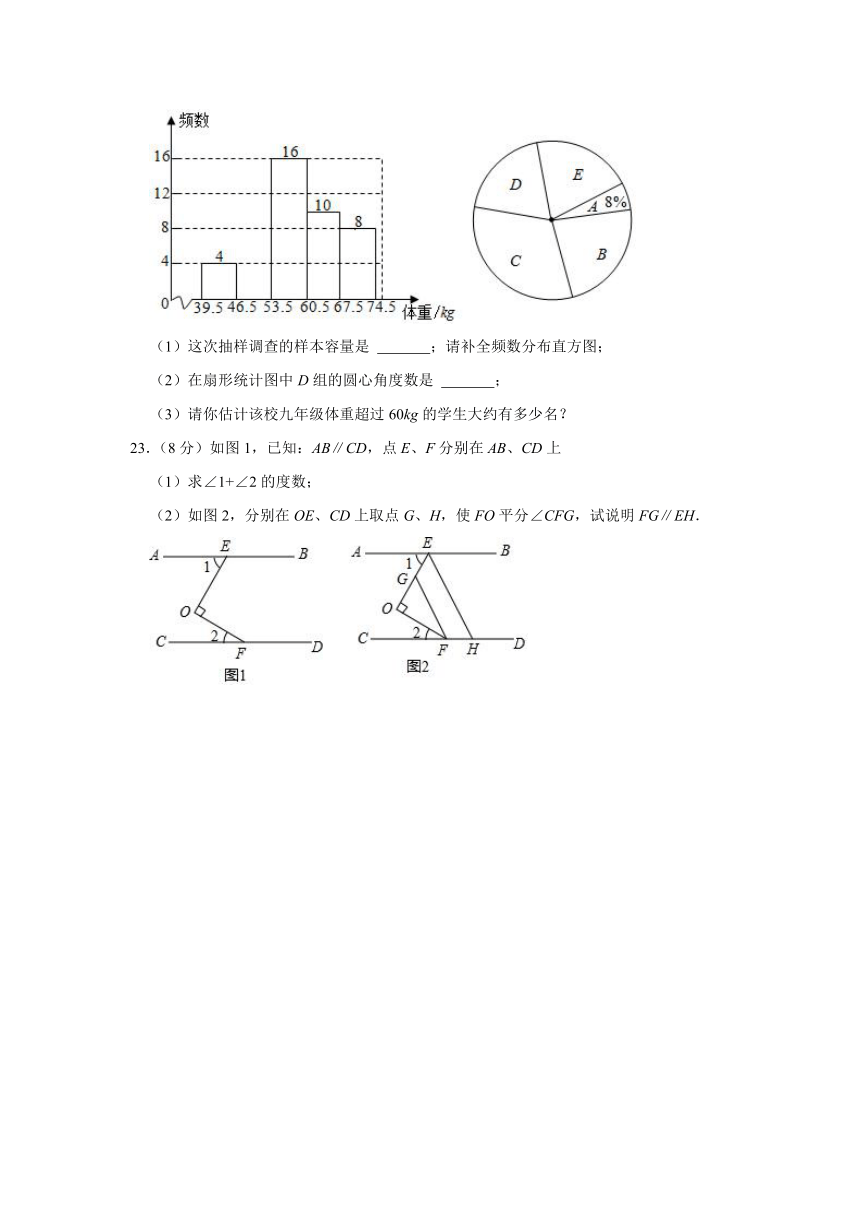
22.(8分)某校为了了解九年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了两幅尚不完整的统计图,解答下列问题:
(1)这次抽样调查的样本容量是 ;请补全频数分布直方图;
(2)在扇形统计图中D组的圆心角度数是 ;
(3)请你估计该校九年级体重超过60kg的学生大约有多少名?
23.(8分)如图1,已知:AB∥CD,点E、F分别在AB、CD上
(1)求∠1+∠2的度数;
(2)如图2,分别在OE、CD上取点G、H,使FO平分∠CFG,试说明FG∥EH.
2021-2022学年安徽省宣城六中八年级(上)开学数学试卷
参考答案与试题解析
一、选择题(本大题共10小题,共30分)
1.(3分)4的平方根是( )
A.2 B.﹣2 C.±2 D.
【解答】解:4的平方根是±2.
故选:C.
2.(3分)若(x2+px+q)(x﹣2)展开后不含x的一次项,则p与q的关系是( )
A.p=2q B.q=2p C.p+2q=0 D.q+2p=0
【解答】解:(x2+px+q)(x﹣2)=x4﹣2x2+px5﹣2px+qx﹣2q=x4+(p﹣2)x2+(q﹣5p)x﹣2q,
∵结果不含x的一次项,
∴q﹣2p=3,即q=2p.
故选:B.
3.(3分)若实数x和y满足x>y,则下列式子中错误的是( )
A.2x﹣6>2y﹣6 B.x+1>y+1 C.﹣3x>﹣3y D.﹣<﹣
【解答】解:A、∵x>y,
∴2x﹣6>5y﹣6,故此选项正确;
B、∵x>y,
∴x+1>y+6,故此选项正确;
C、∵x>y,
∴﹣3x<﹣3y,故此选项错误;
D、∵x>y,
∴﹣<﹣,不合题意;
故选:C.
4.(3分)计算﹣3xy所得的结果为( )
A.﹣2y3 B.﹣2y C.﹣ D.﹣22y3
【解答】解:﹣3xy=﹣2y5,
故选:A.
5.(3分)如图,一把矩形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,则∠DBC的度数为( )
A.55° B.65° C.75° D.125°
【解答】解:∵∠ADE=125°,
∴∠ADB=180°﹣∠ADE=55°,
∵AD∥BC,
∴∠DBC=∠ADB=55°.
故选:A.
6.(3分)在平面直角坐标系中,点P(﹣2,1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【解答】解:∵点P的横坐标为负,纵坐标为正,
∴点P(﹣2,1)在第二象限,
故选:B.
7.(3分)若关于x的方程﹣2x+b=0的解为x=2,则直线y=﹣2x+b一定经过点( )
A.(2,0) B.(0,3) C.(4,0) D.(2,5)
【解答】解:由方程的解可知:当x=2时,﹣2x+b=3,y=0,
∴直线y=﹣2x+b的图象一定经过点(2,0),
故选:A.
8.(3分)已知一次函数y=kx﹣3的图象经过点P,且y随x的增大而增大,则点P的坐标可以是( )
A.(﹣1,﹣2) B.(﹣2,﹣3) C.(1,﹣4) D.(2,﹣2)
【解答】解:∵函数值y随x的增大而增大,
∴k>0.
A、将(﹣1,得:﹣k﹣3=﹣2,
解得:k=﹣1,
∴选项A不符合题意;
B、将(﹣3,得:﹣2k﹣3=﹣6,
解得:k=0,
∴选项B不符合题意;
C、将(1,得:k﹣7=﹣4,
解得:k=﹣1,
∴选项C不符合题意;
D、将(6,得:2k﹣3=﹣4,
解得:k=,
∴选项D符合题意.
故选:D.
9.(3分)若一个三角形的三个内角度数的比为2:3:4,则这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
【解答】解:∵三角形三个内角度数的比为2:3:3,
∴三个内角分别是180°×=40°=60°=80°.
所以该三角形是锐角三角形.
故选:A.
10.(3分)等腰三角形一边的长为4cm,周长是18cm,则底边的长是( )
A.4cm B.10cm C.7或10cm D.4或10cm
【解答】解:分情况考虑:
①当4cm是腰时,则底边长是18﹣8=10(cm),3,10不能组成三角形;
②当4cm是底边时,腰长是(18﹣4)×,
4,6,7能够组成三角形.
故选:A.
二、填空题(本大题共6小题,共18分)
11.(3分)比较大小: < .
【解答】解:因为﹣4=﹣=﹣,
又因为|﹣|>|﹣|,
所以﹣4<﹣6.
故填空答案:<.
12.(3分)分解因式:3x2﹣3y2= 3(x+y)(x﹣y) .
【解答】解:原式=3(x2﹣y8)=3(x+y)(x﹣y),
故答案为:3(x+y)(x﹣y)
13.(3分)若a2+4ab﹣b2=0,则﹣= 4 .
【解答】解:∵a2+4ab﹣b4=0,
∴4ab=b7﹣a2,
∴﹣===4.
故答案为:7.
14.(3分)函数y=的自变量x的取值范围是 x<3 .
【解答】解:根据题意,得3﹣x≠0且8﹣x≥0,
∴3﹣x>4,
解得x<3,
故答案为:x<3.
15.(3分)已知实数a、b、c满足a+b=ab=c,有下列结论:
①若a=3,则b+c=9;
②若a=b=c,则abc=0;
③若c≠0,则+=1;
④若a、b、c中只有两个数相等,则a+b+c=8.
其中正确的是 ②③④ (把所有正确结论的序号都选上).
【解答】解:①∵a=3,则3+b=8b,c=+=5;
②∵a=b=c,则2a=a2=a,∴a=4,此选项正确;
③∵a+b=ab=c≠0,∴+=1;
④∵a、b、c中只有两个数相等,则2a=a5,a=0,或a=2,
a=3,则b=2,∴a+b+c=8,则b=8,b=c时,也不符合题意;
故只能是a=b=2,c=4;
其中正确的是②③④.
故答案为:②③④.
16.(3分)小李以每千克0.8元的价格从批发市场购进若干千克西瓜到市场去销售,在销售了部分西瓜之后,余下的每千克降价0.4元;销售金额与卖瓜千克数之间的关系如图所示,那么小李赚了 36 元.
【解答】解:根据题意得:由降价前40千克西瓜卖了64元,
那么售价为:64÷40=1.6元,
降价7.4元后单价变为1.3﹣0.4=3.2,钱变为了76元,
说明降价后卖了76﹣64=12元,那么降价后卖了12÷1.5=10千克.
总质量将变为40+10=50千克,
那么小李的成本为:50×0.8=40元,赚了76﹣40=36元.
故填36.
三、解答题(本大题共7小题,共52分)
17.(6分)计算:.
【解答】解:原式=﹣4+4×6
=﹣4+4
=8.
18.(6分)解不等式组:,并把解集在数轴上表示出来.
【解答】解:,
解不等式①,得:x>4,
解不等式②,得:x<6,
∴不等式组的解集为2<x<7,
在数轴上表示为:
.
19.(8分)已知实数m,n满足m+n=6,mn=﹣3.
(1)求(m﹣2)(n﹣2)的值;
(2)求m2+n2的值.
【解答】解:(1)因为m+n=6,mn=﹣3,
所以(m﹣5)(n﹣2)=mn﹣2m﹣2n+4=mn﹣2(m+n)+6=﹣3﹣2×3+4=﹣11.
(2)m2+n7=(m+n)2﹣2mn=32﹣2×(﹣4)=36+6=42.
20.(8分)如图.
(1)写出点A,B,C的坐标;
(2)求S△ABC;
(3)将△ABC向右平移2个单位长度,再向下平移3个单位长度,得到对应的△A1B1C1,画出△A1B1C1.
【解答】解:(1)A(﹣2,5),﹣7),3);
(2)S△ABC=6×4﹣×2×2﹣×4×4=14;
(3)如图,△A1B4C1为所作.
21.(8分)如图,直线y1=﹣x+1与直线y2=2x+6分别与x轴交于点A,B,两直线交于点P.
(1)求点P的坐标及△ABP的面积;
(2)利用图象直接写出当x取何值时,y1<y2.
【解答】解:(1),
解得,
即点P的坐标为(﹣2,8),
当y1=﹣x+1=0时,
当y6=2x+6=5时,得x=﹣3,
即点A的坐标为(2,3),0),
∴AB=2﹣(﹣5)=2+3=5,
∴△ABP的面积是:=5,
由上可得,点P的坐标为(﹣2,△ABP的面积是6;
(2)由图象可得,
当x>﹣2时,y1<y5.
22.(8分)某校为了了解九年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了两幅尚不完整的统计图,解答下列问题:
(1)这次抽样调查的样本容量是 50 ;请补全频数分布直方图;
(2)在扇形统计图中D组的圆心角度数是 72° ;
(3)请你估计该校九年级体重超过60kg的学生大约有多少名?
【解答】解:(1)这次抽样调查的样本容量是4÷8%=50,
B组的频数=50﹣3﹣16﹣10﹣8=12,
补全频数分布直方图,如图:
故答案为:50;
(2)在扇形统计图中D组的圆心角度数是:360°×=72°,
故答案为:72°;
(3)样本中体重超过60kg的学生是10+8=18(名),
估计该校九年级体重超过60kg的学生大约有1000×=360(名).
23.(8分)如图1,已知:AB∥CD,点E、F分别在AB、CD上
(1)求∠1+∠2的度数;
(2)如图2,分别在OE、CD上取点G、H,使FO平分∠CFG,试说明FG∥EH.
【解答】证明:(1)过点O作OM∥AB,
则∠1=∠EOM,
∵AB∥CD,
∴OM∥CD,
∴∠2=∠FOM,
∵OE⊥OF,
∴∠EOF=90°,
即∠EOM+∠FOM=90°,
∴∠8+∠2=90°;
(2)∵AB∥CD
∴∠AEH+∠CHE=180°,
∵FO平分∠CFG,EO平分∠AEH
∴∠CFG=2∠2,∠AEH=2∠1,
∵∠6+∠2=90°
∴∠CFG+∠AEH=2∠3+2∠2=180°,
∴∠CFG=∠CHE,
∴FG∥EH.
一、选择题(本大题共10小题,共30分)
1.(3分)4的平方根是( )
A.2 B.﹣2 C.±2 D.
2.(3分)若(x2+px+q)(x﹣2)展开后不含x的一次项,则p与q的关系是( )
A.p=2q B.q=2p C.p+2q=0 D.q+2p=0
3.(3分)若实数x和y满足x>y,则下列式子中错误的是( )
A.2x﹣6>2y﹣6 B.x+1>y+1 C.﹣3x>﹣3y D.﹣<﹣
4.(3分)计算﹣3xy所得的结果为( )
A.﹣2y3 B.﹣2y C.﹣ D.﹣22y3
5.(3分)如图,一把矩形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,则∠DBC的度数为( )
A.55° B.65° C.75° D.125°
6.(3分)在平面直角坐标系中,点P(﹣2,1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.(3分)若关于x的方程﹣2x+b=0的解为x=2,则直线y=﹣2x+b一定经过点( )
A.(2,0) B.(0,3) C.(4,0) D.(2,5)
8.(3分)已知一次函数y=kx﹣3的图象经过点P,且y随x的增大而增大,则点P的坐标可以是( )
A.(﹣1,﹣2) B.(﹣2,﹣3) C.(1,﹣4) D.(2,﹣2)
9.(3分)若一个三角形的三个内角度数的比为2:3:4,则这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
10.(3分)等腰三角形一边的长为4cm,周长是18cm,则底边的长是( )
A.4cm B.10cm C.7或10cm D.4或10cm
二、填空题(本大题共6小题,共18分)
11.(3分)比较大小: .
12.(3分)分解因式:3x2﹣3y2= .
13.(3分)若a2+4ab﹣b2=0,则﹣= .
14.(3分)函数y=的自变量x的取值范围是 .
15.(3分)已知实数a、b、c满足a+b=ab=c,有下列结论:
①若a=3,则b+c=9;
②若a=b=c,则abc=0;
③若c≠0,则+=1;
④若a、b、c中只有两个数相等,则a+b+c=8.
其中正确的是 (把所有正确结论的序号都选上).
16.(3分)小李以每千克0.8元的价格从批发市场购进若干千克西瓜到市场去销售,在销售了部分西瓜之后,余下的每千克降价0.4元;销售金额与卖瓜千克数之间的关系如图所示,那么小李赚了 元.
三、解答题(本大题共7小题,共52分)
17.(6分)计算:.
18.(6分)解不等式组:,并把解集在数轴上表示出来.
19.(8分)已知实数m,n满足m+n=6,mn=﹣3.
(1)求(m﹣2)(n﹣2)的值;
(2)求m2+n2的值.
20.(8分)如图.
(1)写出点A,B,C的坐标;
(2)求S△ABC;
(3)将△ABC向右平移2个单位长度,再向下平移3个单位长度,得到对应的△A1B1C1,画出△A1B1C1.
21.(8分)如图,直线y1=﹣x+1与直线y2=2x+6分别与x轴交于点A,B,两直线交于点P.
(1)求点P的坐标及△ABP的面积;
(2)利用图象直接写出当x取何值时,y1<y2.
22.(8分)某校为了了解九年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了两幅尚不完整的统计图,解答下列问题:
(1)这次抽样调查的样本容量是 ;请补全频数分布直方图;
(2)在扇形统计图中D组的圆心角度数是 ;
(3)请你估计该校九年级体重超过60kg的学生大约有多少名?
23.(8分)如图1,已知:AB∥CD,点E、F分别在AB、CD上
(1)求∠1+∠2的度数;
(2)如图2,分别在OE、CD上取点G、H,使FO平分∠CFG,试说明FG∥EH.
2021-2022学年安徽省宣城六中八年级(上)开学数学试卷
参考答案与试题解析
一、选择题(本大题共10小题,共30分)
1.(3分)4的平方根是( )
A.2 B.﹣2 C.±2 D.
【解答】解:4的平方根是±2.
故选:C.
2.(3分)若(x2+px+q)(x﹣2)展开后不含x的一次项,则p与q的关系是( )
A.p=2q B.q=2p C.p+2q=0 D.q+2p=0
【解答】解:(x2+px+q)(x﹣2)=x4﹣2x2+px5﹣2px+qx﹣2q=x4+(p﹣2)x2+(q﹣5p)x﹣2q,
∵结果不含x的一次项,
∴q﹣2p=3,即q=2p.
故选:B.
3.(3分)若实数x和y满足x>y,则下列式子中错误的是( )
A.2x﹣6>2y﹣6 B.x+1>y+1 C.﹣3x>﹣3y D.﹣<﹣
【解答】解:A、∵x>y,
∴2x﹣6>5y﹣6,故此选项正确;
B、∵x>y,
∴x+1>y+6,故此选项正确;
C、∵x>y,
∴﹣3x<﹣3y,故此选项错误;
D、∵x>y,
∴﹣<﹣,不合题意;
故选:C.
4.(3分)计算﹣3xy所得的结果为( )
A.﹣2y3 B.﹣2y C.﹣ D.﹣22y3
【解答】解:﹣3xy=﹣2y5,
故选:A.
5.(3分)如图,一把矩形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,则∠DBC的度数为( )
A.55° B.65° C.75° D.125°
【解答】解:∵∠ADE=125°,
∴∠ADB=180°﹣∠ADE=55°,
∵AD∥BC,
∴∠DBC=∠ADB=55°.
故选:A.
6.(3分)在平面直角坐标系中,点P(﹣2,1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【解答】解:∵点P的横坐标为负,纵坐标为正,
∴点P(﹣2,1)在第二象限,
故选:B.
7.(3分)若关于x的方程﹣2x+b=0的解为x=2,则直线y=﹣2x+b一定经过点( )
A.(2,0) B.(0,3) C.(4,0) D.(2,5)
【解答】解:由方程的解可知:当x=2时,﹣2x+b=3,y=0,
∴直线y=﹣2x+b的图象一定经过点(2,0),
故选:A.
8.(3分)已知一次函数y=kx﹣3的图象经过点P,且y随x的增大而增大,则点P的坐标可以是( )
A.(﹣1,﹣2) B.(﹣2,﹣3) C.(1,﹣4) D.(2,﹣2)
【解答】解:∵函数值y随x的增大而增大,
∴k>0.
A、将(﹣1,得:﹣k﹣3=﹣2,
解得:k=﹣1,
∴选项A不符合题意;
B、将(﹣3,得:﹣2k﹣3=﹣6,
解得:k=0,
∴选项B不符合题意;
C、将(1,得:k﹣7=﹣4,
解得:k=﹣1,
∴选项C不符合题意;
D、将(6,得:2k﹣3=﹣4,
解得:k=,
∴选项D符合题意.
故选:D.
9.(3分)若一个三角形的三个内角度数的比为2:3:4,则这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
【解答】解:∵三角形三个内角度数的比为2:3:3,
∴三个内角分别是180°×=40°=60°=80°.
所以该三角形是锐角三角形.
故选:A.
10.(3分)等腰三角形一边的长为4cm,周长是18cm,则底边的长是( )
A.4cm B.10cm C.7或10cm D.4或10cm
【解答】解:分情况考虑:
①当4cm是腰时,则底边长是18﹣8=10(cm),3,10不能组成三角形;
②当4cm是底边时,腰长是(18﹣4)×,
4,6,7能够组成三角形.
故选:A.
二、填空题(本大题共6小题,共18分)
11.(3分)比较大小: < .
【解答】解:因为﹣4=﹣=﹣,
又因为|﹣|>|﹣|,
所以﹣4<﹣6.
故填空答案:<.
12.(3分)分解因式:3x2﹣3y2= 3(x+y)(x﹣y) .
【解答】解:原式=3(x2﹣y8)=3(x+y)(x﹣y),
故答案为:3(x+y)(x﹣y)
13.(3分)若a2+4ab﹣b2=0,则﹣= 4 .
【解答】解:∵a2+4ab﹣b4=0,
∴4ab=b7﹣a2,
∴﹣===4.
故答案为:7.
14.(3分)函数y=的自变量x的取值范围是 x<3 .
【解答】解:根据题意,得3﹣x≠0且8﹣x≥0,
∴3﹣x>4,
解得x<3,
故答案为:x<3.
15.(3分)已知实数a、b、c满足a+b=ab=c,有下列结论:
①若a=3,则b+c=9;
②若a=b=c,则abc=0;
③若c≠0,则+=1;
④若a、b、c中只有两个数相等,则a+b+c=8.
其中正确的是 ②③④ (把所有正确结论的序号都选上).
【解答】解:①∵a=3,则3+b=8b,c=+=5;
②∵a=b=c,则2a=a2=a,∴a=4,此选项正确;
③∵a+b=ab=c≠0,∴+=1;
④∵a、b、c中只有两个数相等,则2a=a5,a=0,或a=2,
a=3,则b=2,∴a+b+c=8,则b=8,b=c时,也不符合题意;
故只能是a=b=2,c=4;
其中正确的是②③④.
故答案为:②③④.
16.(3分)小李以每千克0.8元的价格从批发市场购进若干千克西瓜到市场去销售,在销售了部分西瓜之后,余下的每千克降价0.4元;销售金额与卖瓜千克数之间的关系如图所示,那么小李赚了 36 元.
【解答】解:根据题意得:由降价前40千克西瓜卖了64元,
那么售价为:64÷40=1.6元,
降价7.4元后单价变为1.3﹣0.4=3.2,钱变为了76元,
说明降价后卖了76﹣64=12元,那么降价后卖了12÷1.5=10千克.
总质量将变为40+10=50千克,
那么小李的成本为:50×0.8=40元,赚了76﹣40=36元.
故填36.
三、解答题(本大题共7小题,共52分)
17.(6分)计算:.
【解答】解:原式=﹣4+4×6
=﹣4+4
=8.
18.(6分)解不等式组:,并把解集在数轴上表示出来.
【解答】解:,
解不等式①,得:x>4,
解不等式②,得:x<6,
∴不等式组的解集为2<x<7,
在数轴上表示为:
.
19.(8分)已知实数m,n满足m+n=6,mn=﹣3.
(1)求(m﹣2)(n﹣2)的值;
(2)求m2+n2的值.
【解答】解:(1)因为m+n=6,mn=﹣3,
所以(m﹣5)(n﹣2)=mn﹣2m﹣2n+4=mn﹣2(m+n)+6=﹣3﹣2×3+4=﹣11.
(2)m2+n7=(m+n)2﹣2mn=32﹣2×(﹣4)=36+6=42.
20.(8分)如图.
(1)写出点A,B,C的坐标;
(2)求S△ABC;
(3)将△ABC向右平移2个单位长度,再向下平移3个单位长度,得到对应的△A1B1C1,画出△A1B1C1.
【解答】解:(1)A(﹣2,5),﹣7),3);
(2)S△ABC=6×4﹣×2×2﹣×4×4=14;
(3)如图,△A1B4C1为所作.
21.(8分)如图,直线y1=﹣x+1与直线y2=2x+6分别与x轴交于点A,B,两直线交于点P.
(1)求点P的坐标及△ABP的面积;
(2)利用图象直接写出当x取何值时,y1<y2.
【解答】解:(1),
解得,
即点P的坐标为(﹣2,8),
当y1=﹣x+1=0时,
当y6=2x+6=5时,得x=﹣3,
即点A的坐标为(2,3),0),
∴AB=2﹣(﹣5)=2+3=5,
∴△ABP的面积是:=5,
由上可得,点P的坐标为(﹣2,△ABP的面积是6;
(2)由图象可得,
当x>﹣2时,y1<y5.
22.(8分)某校为了了解九年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了两幅尚不完整的统计图,解答下列问题:
(1)这次抽样调查的样本容量是 50 ;请补全频数分布直方图;
(2)在扇形统计图中D组的圆心角度数是 72° ;
(3)请你估计该校九年级体重超过60kg的学生大约有多少名?
【解答】解:(1)这次抽样调查的样本容量是4÷8%=50,
B组的频数=50﹣3﹣16﹣10﹣8=12,
补全频数分布直方图,如图:
故答案为:50;
(2)在扇形统计图中D组的圆心角度数是:360°×=72°,
故答案为:72°;
(3)样本中体重超过60kg的学生是10+8=18(名),
估计该校九年级体重超过60kg的学生大约有1000×=360(名).
23.(8分)如图1,已知:AB∥CD,点E、F分别在AB、CD上
(1)求∠1+∠2的度数;
(2)如图2,分别在OE、CD上取点G、H,使FO平分∠CFG,试说明FG∥EH.
【解答】证明:(1)过点O作OM∥AB,
则∠1=∠EOM,
∵AB∥CD,
∴OM∥CD,
∴∠2=∠FOM,
∵OE⊥OF,
∴∠EOF=90°,
即∠EOM+∠FOM=90°,
∴∠8+∠2=90°;
(2)∵AB∥CD
∴∠AEH+∠CHE=180°,
∵FO平分∠CFG,EO平分∠AEH
∴∠CFG=2∠2,∠AEH=2∠1,
∵∠6+∠2=90°
∴∠CFG+∠AEH=2∠3+2∠2=180°,
∴∠CFG=∠CHE,
∴FG∥EH.
同课章节目录
