4.4.2第一课时 对数函数的图象和性质(一)-学案(Word版)
文档属性
| 名称 | 4.4.2第一课时 对数函数的图象和性质(一)-学案(Word版) |  | |
| 格式 | docx | ||
| 文件大小 | 232.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-17 21:25:22 | ||
图片预览


文档简介
4.4.2 对数函数的图象和性质
第一课时 对数函数的图象和性质(一)-学案
课标要求 素养要求
1.掌握对数函数的图象及简单应用. 2.会利用对数函数的单调性比较大小. 1.借助于对数函数的图象的识别与应用,发展直观想象素养. 2.通过对数函数性质的应用,提升数学运算素养.
自主梳理
对数函数y=logax(a>0,且a≠1)的图象和性质
a>1 0图象
性 质 定义域 (0,+∞)
值域 R
过定点 过定点(1,0),即x=1时,y=0
函数值 的变化 当01时,y>0 当00, 当x>1时,y<0
单调性 在(0,+∞)上是增函数 在(0,+∞)上是减函数
两个单调性相同的对数函数,它们的图象在位于直线x=1右侧的部分是“底大图低”,如图.
自主检验
1.思考辨析,判断正误
(1)函数y=ax与y=logax的单调区间相同.(×)
提示 函数y=ax的单调区间是(-∞,+∞),函数y=logax的单调区间是(0,
+∞),故(1)错.
(2)函数y=loga(x+1)的图象过定点(2,0).(×)
提示 函数y=loga(x+1)的图象过定点(0,0),故(2)错.
(3)若loga2>loga3,则02.对数函数y=logax与y=logbx的图象如图,则( )
A.a<0,b<0 B.a<0,b>0
C.01 D.0答案 C
解析 由图可知y=logbx单调递增,故b>1,y=logax单调递减,故03.若函数f(x)=2loga(2-x)+3(a>0,且a≠1)过定点P,则点P的坐标是________.
答案 (1,3)
解析 令2-x=1,得x=1,f(1)=3,
故P的坐标是(1,3).
4.比较大小:2x2+1________22x.
答案 ≥
解析 ∵x2+1≥2x,且y=2x是增函数,∴2x2+1≥22x.
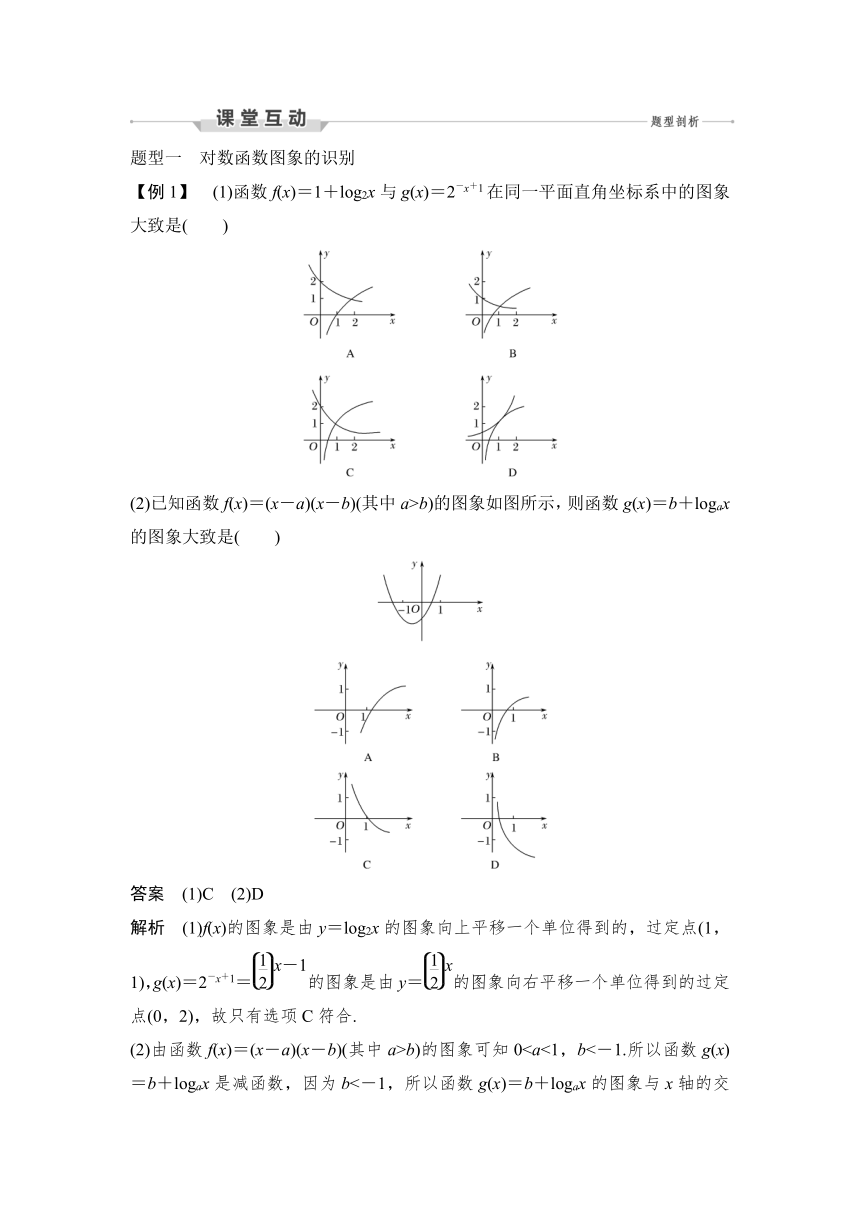
题型一 对数函数图象的识别
【例1】 (1)函数f(x)=1+log2x与g(x)=2-x+1在同一平面直角坐标系中的图象大致是( )
(2)已知函数f(x)=(x-a)(x-b)(其中a>b)的图象如图所示,则函数g(x)=b+logax的图象大致是( )
答案 (1)C (2)D
解析 (1)f(x)的图象是由y=log2x的图象向上平移一个单位得到的,过定点(1,1),g(x)=2-x+1=的图象是由y=的图象向右平移一个单位得到的过定点(0,2),故只有选项C符合.
(2)由函数f(x)=(x-a)(x-b)(其中a>b)的图象可知0思维升华 有关对数函数图象的识别问题,主要依据底数确定图象是上升还是下降、图象位置、图象所过定点、图象的平移与翻折变换等求解.
【训练1】 (1)当a>1时,函数y=logax和y=(1-a)x的图象只能是( )
(2)函数y=log2(1-x)的图象是( )
答案 (1)B (2)C
解析 (1)因为a>1,所以y=logax为增函数,且函数图象过定点(1,0),故排除选项C,D.又因为1-a<0,所以直线y=(1-a)x应过原点,且经过第二象限和第四象限.故选B.
(2)易知函数y=log2(1-x)是减函数,故排除A,D,又函数的定义域为(-∞,1),故可排除B,选C.
题型二 对数函数图象的应用
【例2】 (1)如图是对数函数y=logax的图象,已知a的值取,,,,则相应于C1,C2,C3,C4的a的值依次是( )
A.,,, B.,,,
C.,,, D.,,,
(2)当0A. B.
C.(1,4) D.(,4)
答案 (1)B (2)B
解析 (1)法一 C1,C2的底数都大于1,当x>1时底数大的图低(第一象限内),所以C1,C2对应的a值分别为,,C3,C4的底数都大于0小于1,当x>1时底数大的图低(第一象限内),所以C3,C4对应的a值分别为,,综合以上分析,可得C1,C2,C3,C4对应的a值依次为,,,,故选B.
法二 如图,作直线y=1与四条曲线交于四点,由y=logax=1,得x=a(即交点的横坐标等于底数),所以横坐标小的底数小,所以C1,C2,C3,C4对应的a值分别为,,,.故选B.
(2)当0思维升华 在解决求参数的值或取值范围的问题时,利用函数的图象可事半功倍,
作对数函数的图象时,注意底数的变化对其位置的影响.
【训练2】 设a,b是关于x的方程|lg x|=c的两个不同实数根,且a答案 (0,1)
解析 由题意知,在x∈(0,10)上,y=|lg x|的图象和直线y=c有两个不同交点,作出函数y=|lg x|的图象与直线y=c,如图所示,
结合图象可知,|lg a|=|lg b|=c,又a∴-lg a=lg b=c,∴ab=1,0∴abc的取值范围是(0,1).
题型三 比较对数值的大小
【例3】 (1)若a=log23,b=log32,c=log46,则下列结论正确的是( )
A.bC.c(2)下列不等式成立的是(其中a>0且a≠1)( )
A.loga5.1log2.2
C.log1.1(a+1)答案 (1)D (2)B
解析 (1)因为函数y=log4x在(0,+∞)上是增函数,a=log23=log49>log46>1,log32<1,所以b(2)对于选项A,因为a和1大小的关系不确定,无法确定对数函数的单调性,故A不成立;对于选项B,因为以为底的对数函数是减函数,所以成立;对于选项C,因为以1.1为底的对数函数是增函数,所以不成立;对于选项D,log32.9>0,log0.52.2<0,故不成立,故选B.
思维升华 比较对数值大小时常用的四种方法
(1)同底数的利用对数函数的单调性.
(2)同真数的利用对数函数的图象或用换底公式转化.
(3)底数和真数都不同,找中间量.
(4)若底数为同一参数,则根据底数对对数函数单调性的影响,对底数进行分类讨论.
【训练3】 比较下列各组中两个值的大小:
(1)log31.9,log32;(2)log23,log0.32;
(3)logaπ,loga3.14(a>0,a≠1);(4)log30.2,log40.2.
解 (1)因为y=log3x在(0,+∞)上是增函数,
所以log31.9(2)因为log23>log21=0,log0.32所以log23>log0.32.
(3)当a>1时,函数y=logax在(0,+∞)上是增函数,则有logaπ>loga3.14;
当0则有logaπ综上所得,当a>1时,logaπ>loga3.14;
当0(4)在同一直角坐标系中,作出y=log3x,y=log4x的图象,再作出直线x=0.2,观察图象可得log30.21.在对数函数y=logax中,底数a对其图象直接产生影响,学会以分类的观点认识和掌握对数函数的图象和性质.
2.比较两个对数值的大小及解对数不等式问题,其依据是对数函数的单调性.若对数的底数是字母且范围不明确,一般要分a>1和0
第一课时 对数函数的图象和性质(一)-学案
课标要求 素养要求
1.掌握对数函数的图象及简单应用. 2.会利用对数函数的单调性比较大小. 1.借助于对数函数的图象的识别与应用,发展直观想象素养. 2.通过对数函数性质的应用,提升数学运算素养.
自主梳理
对数函数y=logax(a>0,且a≠1)的图象和性质
a>1 0
性 质 定义域 (0,+∞)
值域 R
过定点 过定点(1,0),即x=1时,y=0
函数值 的变化 当0
单调性 在(0,+∞)上是增函数 在(0,+∞)上是减函数
两个单调性相同的对数函数,它们的图象在位于直线x=1右侧的部分是“底大图低”,如图.
自主检验
1.思考辨析,判断正误
(1)函数y=ax与y=logax的单调区间相同.(×)
提示 函数y=ax的单调区间是(-∞,+∞),函数y=logax的单调区间是(0,
+∞),故(1)错.
(2)函数y=loga(x+1)的图象过定点(2,0).(×)
提示 函数y=loga(x+1)的图象过定点(0,0),故(2)错.
(3)若loga2>loga3,则0
A.a<0,b<0 B.a<0,b>0
C.0
解析 由图可知y=logbx单调递增,故b>1,y=logax单调递减,故0
答案 (1,3)
解析 令2-x=1,得x=1,f(1)=3,
故P的坐标是(1,3).
4.比较大小:2x2+1________22x.
答案 ≥
解析 ∵x2+1≥2x,且y=2x是增函数,∴2x2+1≥22x.
题型一 对数函数图象的识别
【例1】 (1)函数f(x)=1+log2x与g(x)=2-x+1在同一平面直角坐标系中的图象大致是( )
(2)已知函数f(x)=(x-a)(x-b)(其中a>b)的图象如图所示,则函数g(x)=b+logax的图象大致是( )
答案 (1)C (2)D
解析 (1)f(x)的图象是由y=log2x的图象向上平移一个单位得到的,过定点(1,1),g(x)=2-x+1=的图象是由y=的图象向右平移一个单位得到的过定点(0,2),故只有选项C符合.
(2)由函数f(x)=(x-a)(x-b)(其中a>b)的图象可知0
【训练1】 (1)当a>1时,函数y=logax和y=(1-a)x的图象只能是( )
(2)函数y=log2(1-x)的图象是( )
答案 (1)B (2)C
解析 (1)因为a>1,所以y=logax为增函数,且函数图象过定点(1,0),故排除选项C,D.又因为1-a<0,所以直线y=(1-a)x应过原点,且经过第二象限和第四象限.故选B.
(2)易知函数y=log2(1-x)是减函数,故排除A,D,又函数的定义域为(-∞,1),故可排除B,选C.
题型二 对数函数图象的应用
【例2】 (1)如图是对数函数y=logax的图象,已知a的值取,,,,则相应于C1,C2,C3,C4的a的值依次是( )
A.,,, B.,,,
C.,,, D.,,,
(2)当0
C.(1,4) D.(,4)
答案 (1)B (2)B
解析 (1)法一 C1,C2的底数都大于1,当x>1时底数大的图低(第一象限内),所以C1,C2对应的a值分别为,,C3,C4的底数都大于0小于1,当x>1时底数大的图低(第一象限内),所以C3,C4对应的a值分别为,,综合以上分析,可得C1,C2,C3,C4对应的a值依次为,,,,故选B.
法二 如图,作直线y=1与四条曲线交于四点,由y=logax=1,得x=a(即交点的横坐标等于底数),所以横坐标小的底数小,所以C1,C2,C3,C4对应的a值分别为,,,.故选B.
(2)当0
作对数函数的图象时,注意底数的变化对其位置的影响.
【训练2】 设a,b是关于x的方程|lg x|=c的两个不同实数根,且a
解析 由题意知,在x∈(0,10)上,y=|lg x|的图象和直线y=c有两个不同交点,作出函数y=|lg x|的图象与直线y=c,如图所示,
结合图象可知,|lg a|=|lg b|=c,又a
题型三 比较对数值的大小
【例3】 (1)若a=log23,b=log32,c=log46,则下列结论正确的是( )
A.b
A.loga5.1
C.log1.1(a+1)
解析 (1)因为函数y=log4x在(0,+∞)上是增函数,a=log23=log49>log46>1,log32<1,所以b
思维升华 比较对数值大小时常用的四种方法
(1)同底数的利用对数函数的单调性.
(2)同真数的利用对数函数的图象或用换底公式转化.
(3)底数和真数都不同,找中间量.
(4)若底数为同一参数,则根据底数对对数函数单调性的影响,对底数进行分类讨论.
【训练3】 比较下列各组中两个值的大小:
(1)log31.9,log32;(2)log23,log0.32;
(3)logaπ,loga3.14(a>0,a≠1);(4)log30.2,log40.2.
解 (1)因为y=log3x在(0,+∞)上是增函数,
所以log31.9
(3)当a>1时,函数y=logax在(0,+∞)上是增函数,则有logaπ>loga3.14;
当0
当0
2.比较两个对数值的大小及解对数不等式问题,其依据是对数函数的单调性.若对数的底数是字母且范围不明确,一般要分a>1和0
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
