5.4.1 正弦函数、余弦函数的图象-学案(Word版)
文档属性
| 名称 | 5.4.1 正弦函数、余弦函数的图象-学案(Word版) |  | |
| 格式 | docx | ||
| 文件大小 | 239.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-17 21:25:04 | ||
图片预览



文档简介
5.4.1 正弦函数、余弦函数的图象-学案
课标要求 素养要求
1.能利用三角函数的定义,画y=sin x,y=cos x的图象. 2.掌握“五点法”画y=sin x,y=cos x的图象的步骤和方法,能利用“五点法”作出简单的正弦、余弦曲线. 3.理解y=sin x与y=cos x图象之间的联系. 通过利用定义和“五点法”作y=sin x与y=cos x的图象,重点提升学生的数学抽象、逻辑推理和直观想象素养.
自主梳理
1.正弦函数、余弦函数的图象
函数 y=sin x y=cos x
图象
图象画法 “五点法” “五点法”
关键五点 (0,0),(,1),(π,0), (,-1),(2π,0) (0,1),(,0),(π,-1), (,0),(2π,1)
2.(1)正弦函数的图象叫做正弦曲线,是一条“波浪起伏”的连续光滑曲线.
(2)余弦函数y=cos x,x∈R的图象叫做余弦曲线,它是与正弦曲线具有相同形状的“波浪起伏”的连续光滑曲线.
3.正弦函数、余弦函数的值域
(1)y=sin x,x∈R的值域为[-1,1];
(2)y=cos x,x∈R的值域为[-1,1].
自主检验
1.思考辨析,判断正误
(1)正弦函数y=sin x的图象向左右和上下无限伸展.(×)
提示 正弦函数y=sin x的图象向左右无限伸展,但上下限定在直线y=1和y=-1之间.
(2)函数y=sin x与y=sin(-x)的图象完全相同.(×)
提示 二者图象不同,而是关于x轴对称.
(3)直线y=与函数y=sin x,x∈[0,2π]的图象有两个交点.(√)
2.(多选题)用“五点法”作出函数y=3-cos x的图象,下列各点中属于五点作图中的五个关键点的是( )
A.(π,-1) B.(0,2)
C. D.
答案 BCD
解析 A中当x=π时,y=4,故(π,-1)不是关键点,B,C,D都是.
3.函数y=sin(-x),x∈[0,2π]的简图是( )
答案 B
解析 y=sin(-x)=-sin x,故图象与y=sin x的图象关于x轴对称,故选B.
4.函数y=|sin x|的图象( )
A.关于x轴对称 B.关于原点对称
C.关于y轴对称 D.关于坐标轴对称
答案 C
解析 函数y=|sin x|的图象是由y=sin x的图象x轴上方不动,x轴下方的部分关于x轴翻折到x轴上方而得到,易知只有C正确.
题型一 正弦函数、余弦函数图象的初步认识
【例1】 (1)(多选题)下列说法正确的有( )
A.作正弦函数的图象时,单位圆的半径长与y轴的单位长度要一致
B.y=sin x,x∈[0,2π]的图象关于点P(π,0)对称
C.y=sin x,x∈的图象关于直线x=成轴对称
D.正弦函数y=sin x的图象不超出直线y=-1和y=1所夹的区域
(2)函数y=sin |x|的图象是( )
答案 (1)ABD (2)B
解析 (1)由正弦函数的图象可知ABD都正确.
(2)y=sin |x|=
结合选项可知选B.
思维升华 解决正、余弦函数图象的注意点
对于正、余弦函数的图象问题,要画出正确的正弦曲线、余弦曲线,掌握两者的形状相同,只是在坐标系中的位置不同,可以通过相互平移得到.
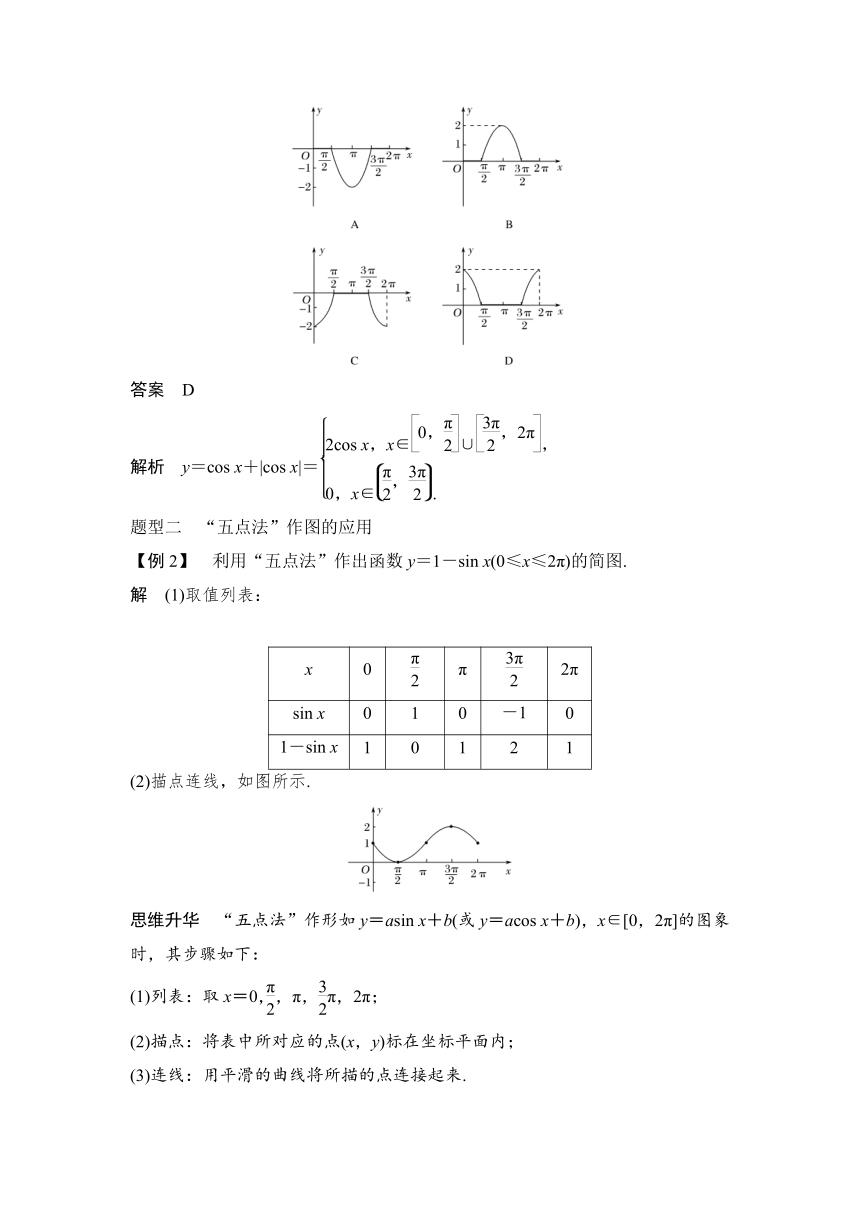
【训练1】 函数y=cos x+|cos x|,x∈[0,2π]的大致图象为( )
答案 D
解析 y=cos x+|cos x|=
题型二 “五点法”作图的应用
【例2】 利用“五点法”作出函数y=1-sin x(0≤x≤2π)的简图.
解 (1)取值列表:
x 0 π 2π
sin x 0 1 0 -1 0
1-sin x 1 0 1 2 1
(2)描点连线,如图所示.
思维升华 “五点法”作形如y=asin x+b(或y=acos x+b),x∈[0,2π]的图象时,其步骤如下:
(1)列表:取x=0,,π,π,2π;
(2)描点:将表中所对应的点(x,y)标在坐标平面内;
(3)连线:用平滑的曲线将所描的点连接起来.
在连线过程中要注意曲线的“凸性”.
【训练2】 利用“五点法”作出函数y=-1-cos x(0≤x≤2π)的简图.
解 (1)取值列表如下:
x 0 π 2π
cos x 1 0 -1 0 1
-1-cos x -2 -1 0 -1 -2
(2)描点连线,如图所示.
题型三 正弦、余弦函数图象的应用
角度1 解有关三角不等式
【例3-1】 利用正弦曲线,求满足解 首先作出y=sin x在[0,2π]上的图象.如图所示,作直线y=,根据特殊角的正弦值,可知该直线与y=sin x,x∈[0,2π]的交点横坐标为和;
作直线y=,该直线与y=sin x,x∈[0,2π]的交点横坐标为和.
观察图象可知,在[0,2π]上,当所以,.
思维升华 用三角函数图象解三角不等式的方法
(1)作出相应正弦函数或余弦函数在[0,2π]上的图象;
(2)写出适合不等式在区间[0,2π]上的解集;
(3)根据公式一写出不等式的解集.
【训练3-1】 在[0,2π]内,求不等式sin x<-的解集.
解 画出y=sin x,x∈[0,2π]的
草图如下.
因为sin=,所以sin=-,sin=-.即在[0,2π]内,满足sin x=-的x=或.可知不等式sin x<-在[0,2π]内的解集是.
角度2 求有关三角函数的定义域
【例3-2】 函数y=log2(2sin x+1)的定义域为________.
答案
解析 要使函数有意义,则必有2sin x+1>0,即sin x>-.画出y=sin x,x∈的草图,如图所示.
当--成立,
所以sin x>-的解集为.
可知函数y=log2(2sin x+1)的定义域为{x+2kπ思维升华 求三角函数定义域时,常常归结为解三角不等式(组),这时可利用基本三角函数的图象直观地求得解集.
【训练3-2】 求下列函数的定义域.
(1)f(x)=;
(2)f(x)=lg cos x+.
解 (1)要使函数有定义,需满足2cos2x+sin x-1≥0,
即2sin2x-sin x-1≤0,
解得-≤sin x≤1,由正弦函数的图象,可得
.
(2)由题意,得x满足不等式组
即作出y=cos x的图象,如图所示.
结合图象可得:
x∈∪∪.
1.对“五点法”画正弦函数图象的理解
(1)与前面学习函数图象的画法类似,在用描点法探究函数图象特征的前提下,若要求精度不高,只要描出函数图象的“关键点”,就可以根据函数图象的变化趋势画出函数图象的草图.
(2)正弦函数图象的关键点是函数图象中最高点、最低点以及与x轴的交点.
2.作函数y=asin x+b的图象的步骤
课标要求 素养要求
1.能利用三角函数的定义,画y=sin x,y=cos x的图象. 2.掌握“五点法”画y=sin x,y=cos x的图象的步骤和方法,能利用“五点法”作出简单的正弦、余弦曲线. 3.理解y=sin x与y=cos x图象之间的联系. 通过利用定义和“五点法”作y=sin x与y=cos x的图象,重点提升学生的数学抽象、逻辑推理和直观想象素养.
自主梳理
1.正弦函数、余弦函数的图象
函数 y=sin x y=cos x
图象
图象画法 “五点法” “五点法”
关键五点 (0,0),(,1),(π,0), (,-1),(2π,0) (0,1),(,0),(π,-1), (,0),(2π,1)
2.(1)正弦函数的图象叫做正弦曲线,是一条“波浪起伏”的连续光滑曲线.
(2)余弦函数y=cos x,x∈R的图象叫做余弦曲线,它是与正弦曲线具有相同形状的“波浪起伏”的连续光滑曲线.
3.正弦函数、余弦函数的值域
(1)y=sin x,x∈R的值域为[-1,1];
(2)y=cos x,x∈R的值域为[-1,1].
自主检验
1.思考辨析,判断正误
(1)正弦函数y=sin x的图象向左右和上下无限伸展.(×)
提示 正弦函数y=sin x的图象向左右无限伸展,但上下限定在直线y=1和y=-1之间.
(2)函数y=sin x与y=sin(-x)的图象完全相同.(×)
提示 二者图象不同,而是关于x轴对称.
(3)直线y=与函数y=sin x,x∈[0,2π]的图象有两个交点.(√)
2.(多选题)用“五点法”作出函数y=3-cos x的图象,下列各点中属于五点作图中的五个关键点的是( )
A.(π,-1) B.(0,2)
C. D.
答案 BCD
解析 A中当x=π时,y=4,故(π,-1)不是关键点,B,C,D都是.
3.函数y=sin(-x),x∈[0,2π]的简图是( )
答案 B
解析 y=sin(-x)=-sin x,故图象与y=sin x的图象关于x轴对称,故选B.
4.函数y=|sin x|的图象( )
A.关于x轴对称 B.关于原点对称
C.关于y轴对称 D.关于坐标轴对称
答案 C
解析 函数y=|sin x|的图象是由y=sin x的图象x轴上方不动,x轴下方的部分关于x轴翻折到x轴上方而得到,易知只有C正确.
题型一 正弦函数、余弦函数图象的初步认识
【例1】 (1)(多选题)下列说法正确的有( )
A.作正弦函数的图象时,单位圆的半径长与y轴的单位长度要一致
B.y=sin x,x∈[0,2π]的图象关于点P(π,0)对称
C.y=sin x,x∈的图象关于直线x=成轴对称
D.正弦函数y=sin x的图象不超出直线y=-1和y=1所夹的区域
(2)函数y=sin |x|的图象是( )
答案 (1)ABD (2)B
解析 (1)由正弦函数的图象可知ABD都正确.
(2)y=sin |x|=
结合选项可知选B.
思维升华 解决正、余弦函数图象的注意点
对于正、余弦函数的图象问题,要画出正确的正弦曲线、余弦曲线,掌握两者的形状相同,只是在坐标系中的位置不同,可以通过相互平移得到.
【训练1】 函数y=cos x+|cos x|,x∈[0,2π]的大致图象为( )
答案 D
解析 y=cos x+|cos x|=
题型二 “五点法”作图的应用
【例2】 利用“五点法”作出函数y=1-sin x(0≤x≤2π)的简图.
解 (1)取值列表:
x 0 π 2π
sin x 0 1 0 -1 0
1-sin x 1 0 1 2 1
(2)描点连线,如图所示.
思维升华 “五点法”作形如y=asin x+b(或y=acos x+b),x∈[0,2π]的图象时,其步骤如下:
(1)列表:取x=0,,π,π,2π;
(2)描点:将表中所对应的点(x,y)标在坐标平面内;
(3)连线:用平滑的曲线将所描的点连接起来.
在连线过程中要注意曲线的“凸性”.
【训练2】 利用“五点法”作出函数y=-1-cos x(0≤x≤2π)的简图.
解 (1)取值列表如下:
x 0 π 2π
cos x 1 0 -1 0 1
-1-cos x -2 -1 0 -1 -2
(2)描点连线,如图所示.
题型三 正弦、余弦函数图象的应用
角度1 解有关三角不等式
【例3-1】 利用正弦曲线,求满足
作直线y=,该直线与y=sin x,x∈[0,2π]的交点横坐标为和.
观察图象可知,在[0,2π]上,当
思维升华 用三角函数图象解三角不等式的方法
(1)作出相应正弦函数或余弦函数在[0,2π]上的图象;
(2)写出适合不等式在区间[0,2π]上的解集;
(3)根据公式一写出不等式的解集.
【训练3-1】 在[0,2π]内,求不等式sin x<-的解集.
解 画出y=sin x,x∈[0,2π]的
草图如下.
因为sin=,所以sin=-,sin=-.即在[0,2π]内,满足sin x=-的x=或.可知不等式sin x<-在[0,2π]内的解集是.
角度2 求有关三角函数的定义域
【例3-2】 函数y=log2(2sin x+1)的定义域为________.
答案
解析 要使函数有意义,则必有2sin x+1>0,即sin x>-.画出y=sin x,x∈的草图,如图所示.
当-
所以sin x>-的解集为.
可知函数y=log2(2sin x+1)的定义域为{x+2kπ
【训练3-2】 求下列函数的定义域.
(1)f(x)=;
(2)f(x)=lg cos x+.
解 (1)要使函数有定义,需满足2cos2x+sin x-1≥0,
即2sin2x-sin x-1≤0,
解得-≤sin x≤1,由正弦函数的图象,可得
.
(2)由题意,得x满足不等式组
即作出y=cos x的图象,如图所示.
结合图象可得:
x∈∪∪.
1.对“五点法”画正弦函数图象的理解
(1)与前面学习函数图象的画法类似,在用描点法探究函数图象特征的前提下,若要求精度不高,只要描出函数图象的“关键点”,就可以根据函数图象的变化趋势画出函数图象的草图.
(2)正弦函数图象的关键点是函数图象中最高点、最低点以及与x轴的交点.
2.作函数y=asin x+b的图象的步骤
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
