3.1.2函数的概念(共26张PPT)
文档属性
| 名称 | 3.1.2函数的概念(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 609.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-16 13:23:19 | ||
图片预览






文档简介
(共26张PPT)
第三章
第二课时 函数的概念(二)
1.会判断两个函数是否为同一函数.
2.能正确使用区间表示数集.
3.会求一些简单函数的值域.
课标要求
素养要求
1.通过对区间概念的理解及判断两个函数为同一函数,提升数学抽象素养.
2.通过求一些简单函数的值域,提升逻辑推理、数学运算素养.
课前预习
知识探究
1
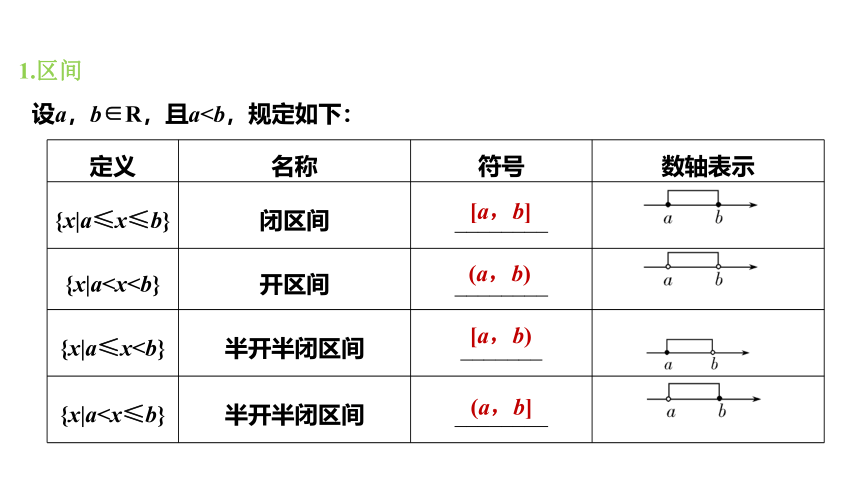
1.区间
设a,b∈R,且a定义 名称 符号 数轴表示
{x|a≤x≤b} 闭区间 ________
{x|a{x|a≤x{x|a[a,b]
(a,b)
[a,b)
(a,b]
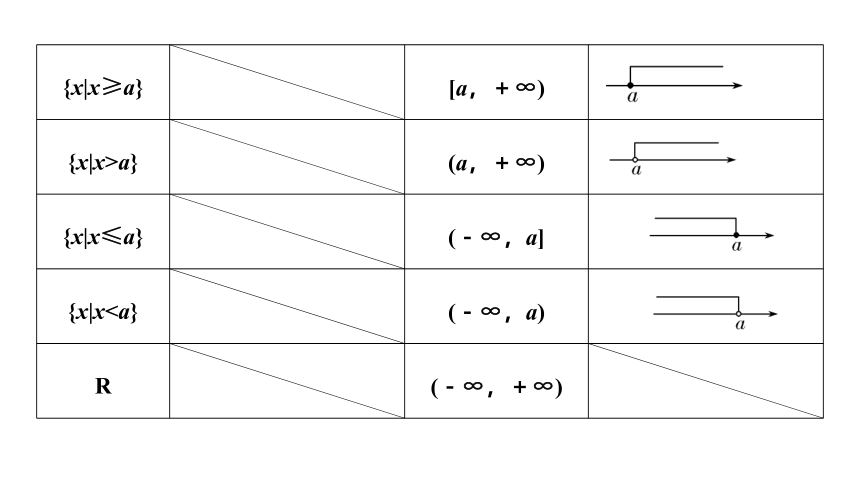
{x|x≥a} [a,+∞)
{x|x>a} (a,+∞)
{x|x≤a} (-∞,a]
{x|xR (-∞,+∞)
2.同一个函数
(1)前提条件:①定义域______;②对应关系______.
(2)结论:这两个函数为同一个函数.
相同
相同
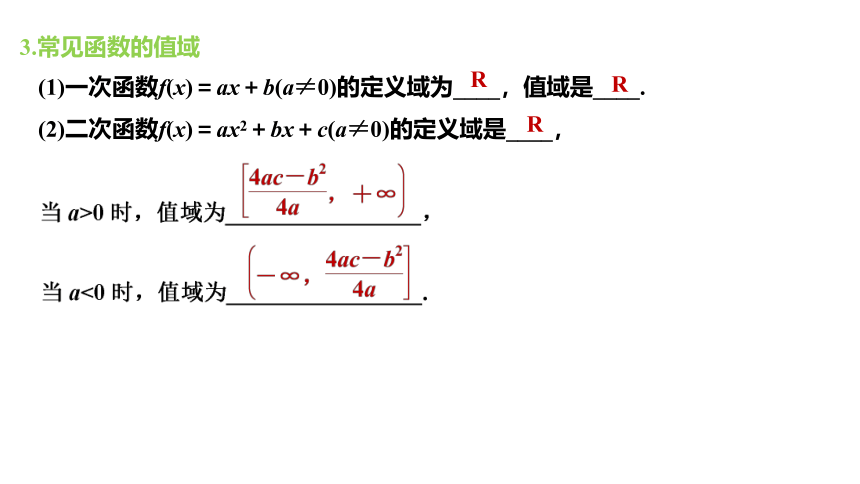
(1)一次函数f(x)=ax+b(a≠0)的定义域为____,值域是____.
(2)二次函数f(x)=ax2+bx+c(a≠0)的定义域是____,
3.常见函数的值域
R
R
R
1.思考辨析,判断正误
(1)已知定义域和对应关系就可以确定一个函数.( )
(2)两个函数的定义域和值域相同就表示同一函数.( )
提示 两个函数的定义域、值域相同,而对应关系不一定相同.
(3)函数y=1+x2的值域为(1,+∞).( )
提示 y=1+x2的值域为[1,+∞).
√
×
×
2.下表表示y是x的函数,则函数的值域是( )
D
A.{y|-1≤y≤1} B.R
C.{y|2≤y≤3} D.{-1,0,1}
x x<2 2≤x≤3 x>3
y -1 0 1
解析 由表格知,对应的y的值为-1,0,1,故选D.
3.(多选题)下列函数是同一函数的是( )
BD
解析 选项A中的两个函数的定义域不同;
选项C中的两个函数的对应关系不同,
选项BD中的函数的定义域和对应关系都相同,是同一函数.
{x|1≤x<2}
4.区间[1,2)表示的集合为____________.
解析 根据区间的定义,可表示为{x|1≤x<2}.
课堂互动
题型剖析
2
题型一 区间的应用
【例1】 把下列数集用区间表示:
(1){x|x≥-1};
(2){x|x<0};
(3){x|-1(4){x|0解 (1){x|x≥-1}=[-1,+∞);
(2){x|x<0}=(-∞,0);
(3){x|-1(4){x|0用区间表示数集的方法:
(1)区间左端点值小于右端点值;
(2)区间两端点之间用“,”隔开;
(3)含端点值的一端用中括号,不含端点值的一端用小括号;
(4)以“-∞”,“+∞”为区间的一端时,这端必须用小括号.
思维升华
【训练1】 (1)用区间表示{x|x≥0且x≠2}为____________________.
(2)已知区间[a,2a+1],则a的取值范围是______________.
解析 (1){x|x≥0且x≠2}=[0,2)∪(2,+∞).
(2)由2a+1>a,得a>-1,则a的取值范围为(-1,+∞).
[0,2)∪(2,+∞)
(-1,+∞)
【例2】 (1)下列各组函数:
题型二 同一函数的判断
⑤
解析 ①f(x)与g(x)的定义域不同,不是同一函数;
②f(x)与g(x)的对应关系不同,不是同一函数;
③f(x)=|x+3|,与g(x)的对应关系不同,不是同一函数;
④f(x)与g(x)的定义域不同,不是同一函数;
⑤f(x)与g(x)的定义域、对应关系皆相同,故是同一函数.
判断两个函数为同一函数应注意的三点:
(1)定义域、对应关系两者中只要有一个不相同就不是同一函数,即使定义域与值域都相同,也不一定是同一函数.
(2)函数是两个数集之间的对应关系,所以用什么字母表示自变量、因变量是没有限制的.
(3)在化简解析式时,必须是等价变形.
思维升华
【训练2】 (1)下列各组函数是同一函数的是( )
D
解析 (1)A,B,C中的两函数定义域均不相同,故选D.
(2)下列各组函数是同一函数的是________(填序号).
②③
对应关系与定义域均相同,故是同一函数;
③f(x)=x2-2x-1与g(t)=t2-2t-1,
对应关系和定义域均相同,故是同一函数.
【例3】 求下列函数的值域:
题型三 求函数的值域
(2)(观察法)∵x∈{-2,-1,0,1,2,3},
∴把x代入y=x2-2x+3得y=11,6,3,2,
∴y=x2-2x+3的值域为{2,3,6,11}.
求函数值域的常用方法
(1)观察法:通过对解析式的简单变形和观察,利用熟知的基本函数的值域,求出函数的值域.
(2)配方法:若函数是二次函数形式,即可化为y=ax2+bx+c(a≠0)型的函数,则可通过配方再结合二次函数的性质求值域,但要注意给定区间的二次函数最值的求法.
(3)换元法:通过对函数的解析式进行适当换元,可将复杂的函数化归为简单的函数,从而利用基本函数自变量的取值范围求函数的值域.
(4)分离常数法:此方法主要是针对分式函数,即将分式函数转化为“反比例函数”的形式,便于求值域.
思维升华
【训练3】 求下列函数的值域:
(2)y=x2-4x+6=(x-2)2+2,
因为1≤x≤5,由函数图象可知y∈[2,11].
1.区间实质上是数轴上某一线段或射线上的所有点所对应的实数的取值集合,即用端点所对应的数、“+∞”(正无穷大)、“-∞”(负无穷大)、方括号(包含端点)、小圆括号(不包含端点)等来表示的部分实数组成的集合.
2.同一函数的概念的理解
(1)函数有三个要素:定义域、值域、对应关系.函数的定义域和对应关系共同确定函数的值域,因此当且仅当两个函数的定义域和对应关系都分别相同时,这两个函数才是同一个函数.
(2)定义域和值域都分别相同的两个函数,它们不一定是同一函数,因为函数对应关系不一定相同.
课堂小结
第三章
第二课时 函数的概念(二)
1.会判断两个函数是否为同一函数.
2.能正确使用区间表示数集.
3.会求一些简单函数的值域.
课标要求
素养要求
1.通过对区间概念的理解及判断两个函数为同一函数,提升数学抽象素养.
2.通过求一些简单函数的值域,提升逻辑推理、数学运算素养.
课前预习
知识探究
1
1.区间
设a,b∈R,且a
{x|a≤x≤b} 闭区间 ________
{x|a
(a,b)
[a,b)
(a,b]
{x|x≥a} [a,+∞)
{x|x>a} (a,+∞)
{x|x≤a} (-∞,a]
{x|x
2.同一个函数
(1)前提条件:①定义域______;②对应关系______.
(2)结论:这两个函数为同一个函数.
相同
相同
(1)一次函数f(x)=ax+b(a≠0)的定义域为____,值域是____.
(2)二次函数f(x)=ax2+bx+c(a≠0)的定义域是____,
3.常见函数的值域
R
R
R
1.思考辨析,判断正误
(1)已知定义域和对应关系就可以确定一个函数.( )
(2)两个函数的定义域和值域相同就表示同一函数.( )
提示 两个函数的定义域、值域相同,而对应关系不一定相同.
(3)函数y=1+x2的值域为(1,+∞).( )
提示 y=1+x2的值域为[1,+∞).
√
×
×
2.下表表示y是x的函数,则函数的值域是( )
D
A.{y|-1≤y≤1} B.R
C.{y|2≤y≤3} D.{-1,0,1}
x x<2 2≤x≤3 x>3
y -1 0 1
解析 由表格知,对应的y的值为-1,0,1,故选D.
3.(多选题)下列函数是同一函数的是( )
BD
解析 选项A中的两个函数的定义域不同;
选项C中的两个函数的对应关系不同,
选项BD中的函数的定义域和对应关系都相同,是同一函数.
{x|1≤x<2}
4.区间[1,2)表示的集合为____________.
解析 根据区间的定义,可表示为{x|1≤x<2}.
课堂互动
题型剖析
2
题型一 区间的应用
【例1】 把下列数集用区间表示:
(1){x|x≥-1};
(2){x|x<0};
(3){x|-1
(2){x|x<0}=(-∞,0);
(3){x|-1
(1)区间左端点值小于右端点值;
(2)区间两端点之间用“,”隔开;
(3)含端点值的一端用中括号,不含端点值的一端用小括号;
(4)以“-∞”,“+∞”为区间的一端时,这端必须用小括号.
思维升华
【训练1】 (1)用区间表示{x|x≥0且x≠2}为____________________.
(2)已知区间[a,2a+1],则a的取值范围是______________.
解析 (1){x|x≥0且x≠2}=[0,2)∪(2,+∞).
(2)由2a+1>a,得a>-1,则a的取值范围为(-1,+∞).
[0,2)∪(2,+∞)
(-1,+∞)
【例2】 (1)下列各组函数:
题型二 同一函数的判断
⑤
解析 ①f(x)与g(x)的定义域不同,不是同一函数;
②f(x)与g(x)的对应关系不同,不是同一函数;
③f(x)=|x+3|,与g(x)的对应关系不同,不是同一函数;
④f(x)与g(x)的定义域不同,不是同一函数;
⑤f(x)与g(x)的定义域、对应关系皆相同,故是同一函数.
判断两个函数为同一函数应注意的三点:
(1)定义域、对应关系两者中只要有一个不相同就不是同一函数,即使定义域与值域都相同,也不一定是同一函数.
(2)函数是两个数集之间的对应关系,所以用什么字母表示自变量、因变量是没有限制的.
(3)在化简解析式时,必须是等价变形.
思维升华
【训练2】 (1)下列各组函数是同一函数的是( )
D
解析 (1)A,B,C中的两函数定义域均不相同,故选D.
(2)下列各组函数是同一函数的是________(填序号).
②③
对应关系与定义域均相同,故是同一函数;
③f(x)=x2-2x-1与g(t)=t2-2t-1,
对应关系和定义域均相同,故是同一函数.
【例3】 求下列函数的值域:
题型三 求函数的值域
(2)(观察法)∵x∈{-2,-1,0,1,2,3},
∴把x代入y=x2-2x+3得y=11,6,3,2,
∴y=x2-2x+3的值域为{2,3,6,11}.
求函数值域的常用方法
(1)观察法:通过对解析式的简单变形和观察,利用熟知的基本函数的值域,求出函数的值域.
(2)配方法:若函数是二次函数形式,即可化为y=ax2+bx+c(a≠0)型的函数,则可通过配方再结合二次函数的性质求值域,但要注意给定区间的二次函数最值的求法.
(3)换元法:通过对函数的解析式进行适当换元,可将复杂的函数化归为简单的函数,从而利用基本函数自变量的取值范围求函数的值域.
(4)分离常数法:此方法主要是针对分式函数,即将分式函数转化为“反比例函数”的形式,便于求值域.
思维升华
【训练3】 求下列函数的值域:
(2)y=x2-4x+6=(x-2)2+2,
因为1≤x≤5,由函数图象可知y∈[2,11].
1.区间实质上是数轴上某一线段或射线上的所有点所对应的实数的取值集合,即用端点所对应的数、“+∞”(正无穷大)、“-∞”(负无穷大)、方括号(包含端点)、小圆括号(不包含端点)等来表示的部分实数组成的集合.
2.同一函数的概念的理解
(1)函数有三个要素:定义域、值域、对应关系.函数的定义域和对应关系共同确定函数的值域,因此当且仅当两个函数的定义域和对应关系都分别相同时,这两个函数才是同一个函数.
(2)定义域和值域都分别相同的两个函数,它们不一定是同一函数,因为函数对应关系不一定相同.
课堂小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
